在你的笔记本电脑或手机上直接运行强大的大型语言模型 (LLMs) ，如 Llama-3 或 Mistral，而不依赖云端，这个梦想是诱人的。它承诺了隐私、更低的延迟以及离线能力。然而，现实往往是与硬件限制的艰难斗争。这些模型计算量大且极其耗费内存。

加速这些模型最有效的方法之一是激活稀疏化 (activation sparsification) 。 其核心思想很简单: 如果一个神经元的激活值接近于零，我们可以将其视为完全为零，从而跳过与之相关的数学运算。

虽然这一概念对于使用 ReLU 激活函数 (天然会输出大量零值) 的旧模型非常有效，但现代 LLM 使用的是像 SwiGLU 这样复杂的函数。这些函数提高了智能程度，但很少输出纯粹的零，这使得稀疏化变得困难。现有的方法试图通过切断小数值来强制稀疏化，但往往极其盲目，从而损害了模型的智能。

在这篇文章中，我们将深入探讨一篇研究论文，该论文介绍了 CHESS (基于通道级阈值化和选择性稀疏化，CHannel-wise thrEsholding and Selective Sparsification) 。研究人员提出了一种更智能、基于统计学基础的方法来修剪激活值，在极小的精度损失下，将推理速度提高了 1.27 倍。

问题所在: 为什么简单的修剪会失败

要理解 CHESS，我们首先需要了解现代 LLM 中使用的前馈网络 (FFN) 的架构。FFN 模块通常遵循以下结构:

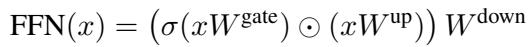
FFN 模块的数学公式。

在这里，输入 \(x\) 分别通过“gate”矩阵和“up”矩阵进行投影。Gate 经过激活函数 \(\sigma\) (如 SwiGLU) ，与“up”投影进行逐元素相乘，最后进行“down”投影。

中间激活值定义如下:

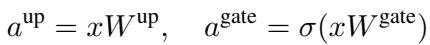
Up 和 gate 激活值的定义。

稀疏化的目标是将 \(a^{\text{gate}}\) 中的某些元素设为零，以便我们可以跳过后续的乘法运算。现有的方法，如一种名为 CATS 的技术，使用一个简单的阈值: 如果 \(a^{\text{gate}}\) 中的值很小，就将其修剪掉。

这种方法的缺陷在于它只关注 \(a^{\text{gate}}\) 的幅度，而忽略了 \(a^{\text{up}}\)。然而，如果 \(a^{\text{up}}\) 非常大，即使是很小的 \(a^{\text{gate}}\) 也会对最终输出产生显著影响。修剪它会导致巨大的误差。

CHESS 方法

CHESS 的作者们重新构想了这个问题。他们不再问“哪些值很小？”，而是问“哪些值如果被移除，会对下一层造成最小的误差？”

1. 重构目标

研究人员在数学上将目标定义为最小化原始输出与稀疏化输出之间的差异。我们需要找到一个修剪后的版本 \(\hat{a}^{\text{gate}}\) 来解决这个最小化问题:

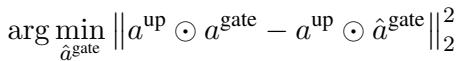
最小化稀疏化误差的优化目标。

通过对此进行分解，他们推导出了一个具体的误差计算公式。为了最大限度地减少对模型的损害，我们应该修剪那些“up”和“gate”激活值乘积最小的元素。这引出了重要性评分 (importance score) 的定义:

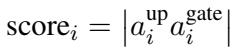
重要性评分计算。

这个等式揭示了核心洞察: 你不能仅凭 gate 值来决定修剪哪个激活值；你必须同时考虑“up”投影。

2. 通道级阈值化 (CWT)

这里存在一个计算上的难题。要计算上述确切的重要性评分，你必须先计算出 \(a^{\text{up}}\)。但稀疏化的全部意义就在于避免做额外的计算。如果为了决定删除什么而计算了所有东西，我们就没有节省任何时间。

研究人员通过分析激活值的统计分布找到了一个巧妙的变通方法。他们观察到，虽然激活值在不同输入之间变化剧烈，但特定通道 (列) 的 \(a^{\text{up}}\) 的平均幅度保持一致。

以此来看看 Llama-3-8B 模型中三个不同通道的分布情况:

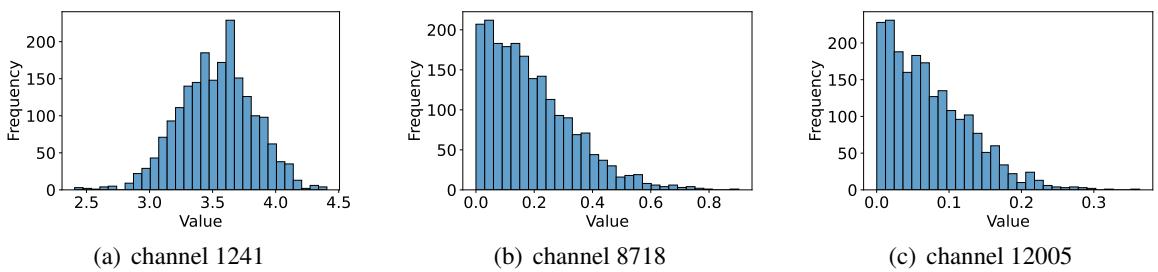
不同通道在不同输入下的绝对激活值分布。

注意到这些分布有多么独特了吗？通道 1241 (左) 集中在 3.5 附近，而通道 8718 (中) 聚集在 0 附近。这种稳定性允许研究人员使用样本数据集上的期望值 (平均值) 来近似估计“up”值:

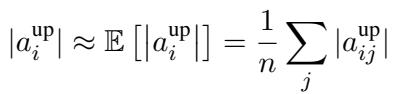
使用期望值近似 up 激活值。

通过将其代入重要性评分，他们创建了一个无需在推理期间计算 \(a^{\text{up}}\) 的新指标。然后，他们为每个通道 \(i\) 确定一个特定的阈值 \(t_i\)。这就是通道级阈值化 (Channel-Wise Thresholding) 。

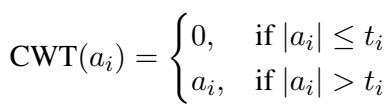
通道级阈值化函数。

如果一个激活值低于其通道特定的阈值，它就会被归零。这种方法尊重了一个事实，即某些通道天生就更“响亮” (具有更高的数值) ，需要更高的阈值才能被有效修剪。

3. 注意力机制中的选择性稀疏化

虽然 FFN 层占据了大部分参数，但注意力模块 (Attention modules) 也会增加延迟。然而，注意力层非常敏感。激进地修剪它们通常会破坏模型。

作者对注意力投影中的误差函数应用了泰勒展开分析。

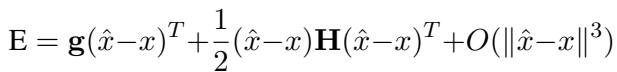
误差函数的泰勒展开。

通过简化和分析权重，他们发现注意力投影的权重矩阵中的行具有相似的范数 (幅度) 。

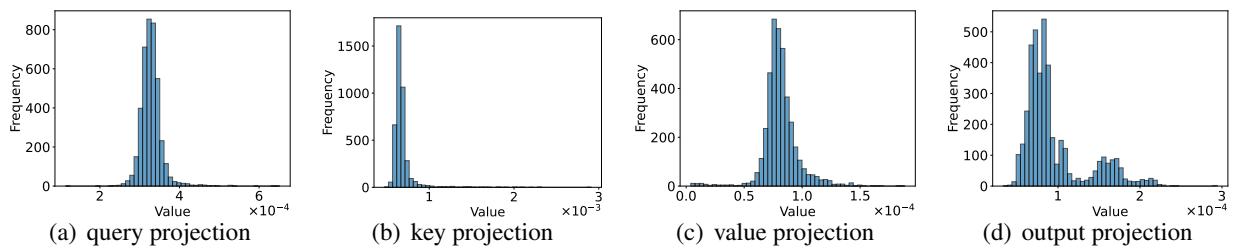
注意力投影中权重行范数的分布。

由于这些范数相似，复杂的优化问题在注意力层中简化回了基于幅度的修剪:

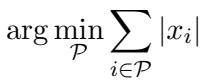
简化的注意力优化目标。

然而，将其应用于注意力机制的每一个部分 (Query, Key, Value, Output) 会导致过多的精度损失。研究人员提出了选择性稀疏化 (Selective Sparsification) 。 他们仅对 Query (查询) 和 Output (输出) 投影应用阈值化，而保持 Key (键) 和 Value (值) 投影不变。

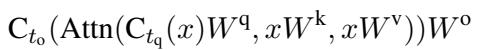
注意力机制中的选择性稀疏化公式。

这种策略取得了一种平衡: 它减少了足够的内存访问和计算以获得速度提升，同时保留了 Key/Value 对中对于准确推理所需的关键信息流。

4. 高效的稀疏内核

理论上的稀疏性并不自动意味着速度。标准硬件 (CPU/GPU) 喜欢密集矩阵。为了实现 CHESS 的优势，作者编写了自定义软件内核 (kernels) 。

他们实现了两个特定的操作:

  1. spvmm: 稀疏向量-矩阵乘法 (Sparse Vector-Matrix Multiplication，当输入向量稀疏时使用) 。
  2. vmmsp: 带输出稀疏性的向量-矩阵乘法 (Vector-Matrix Multiplication with Output Sparsity，当我们计算密集向量但立即用零掩码覆盖时使用) 。

性能差异是显著的。下图比较了自定义 CHESS 内核 (橙色) 与标准 PyTorch 密集内核 (蓝色) 的延迟。

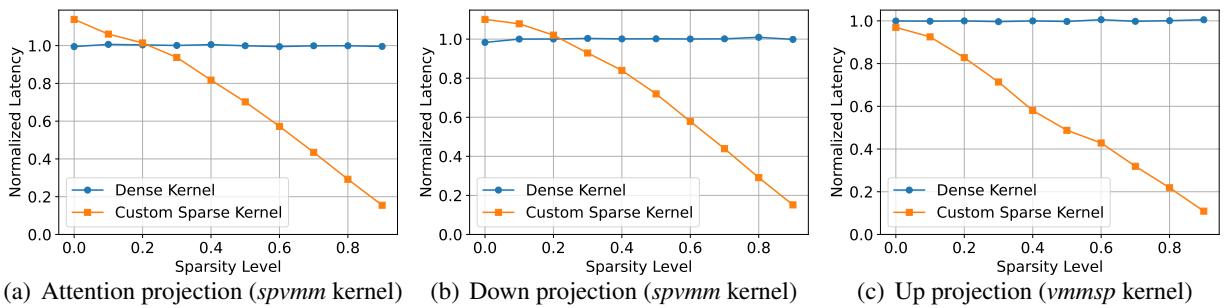
自定义稀疏内核与 PyTorch 密集内核的延迟比较。

随着稀疏度水平 (x 轴) 的增加，自定义内核变得明显更快，而标准内核几乎没有任何收益。

实验结果

CHESS 真的有效吗？研究人员在 Llama-2 (7B, 13B, 70B)、Llama-3-8B 和 Mistral-7B 上，跨 8 个标准下游任务 (如 ARC, HellaSwag 和 PIQA) 对其进行了测试。

精度保持

下表 1 展示了结果。 CHESS w/ (带注意力稀疏化) 和 CHESS w/o (不带注意力稀疏化) 与基础模型 (Base model) 和 CATS 方法进行了比较。

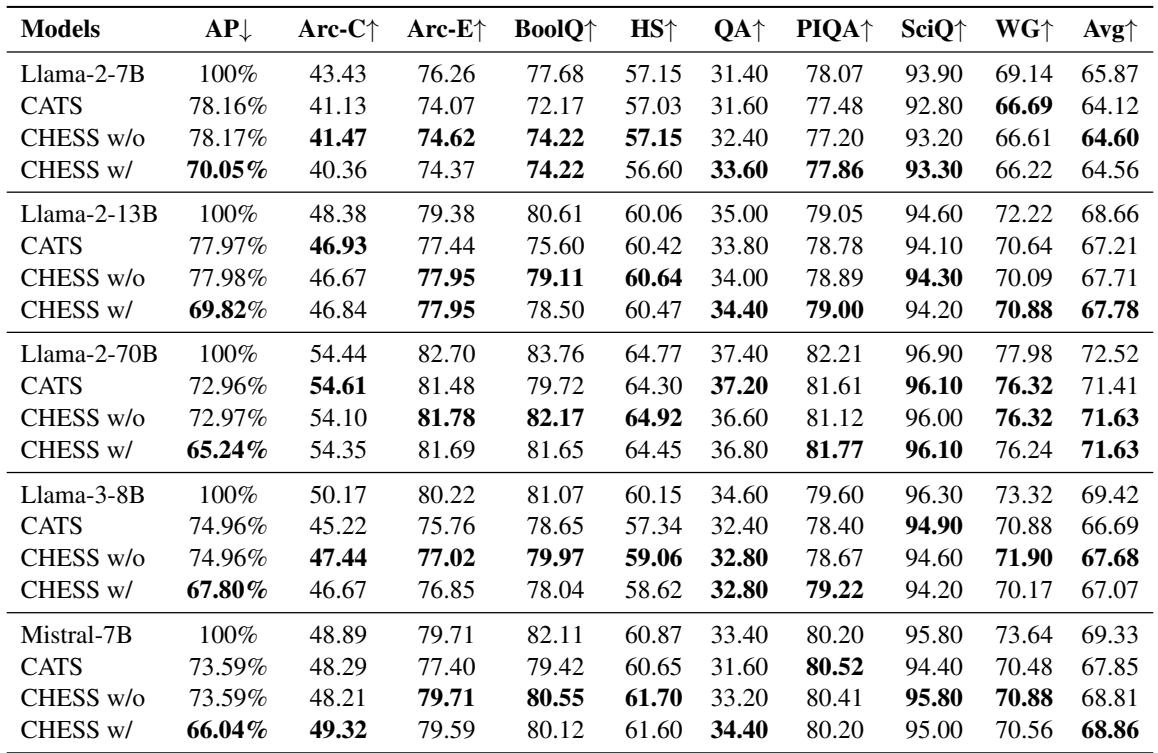
不同模型在下游任务上的推理精度比较。

数据中的关键结论:

  • 更低的降级: CHESS 始终优于 CATS。例如，在 Llama-3-8B 上，CHESS w/o 的平均得分为 67.68，显著高于 CATS 的 66.69。
  • 鲁棒性: 即使包含注意力稀疏化 (CHESS w/) ，与基线相比性能下降也很小，而 CATS 则遭受了更显著的损失。

速度提升

主要目标是速度。下图展示了在 CPU 上的端到端推理加速比。

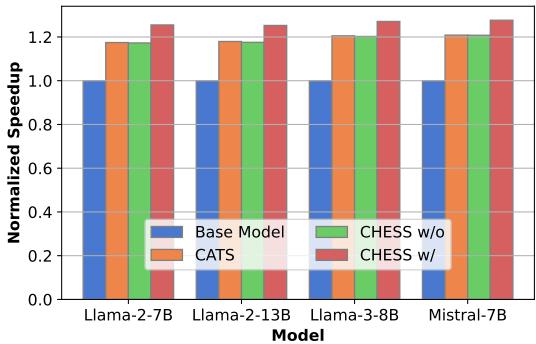
端到端推理加速比比较。

CHESS (红色条形) 在所有模型中都实现了最高的加速比，在 Llama-3 和 Mistral 上达到了约 1.27 倍的推理速度。这对于在边缘设备上运行的实时应用程序来说是一个切实的改进。

权衡: 性能与稀疏性

最后，可视化模型在我们试图让它更快 (更稀疏) 时的表现是很重要的。

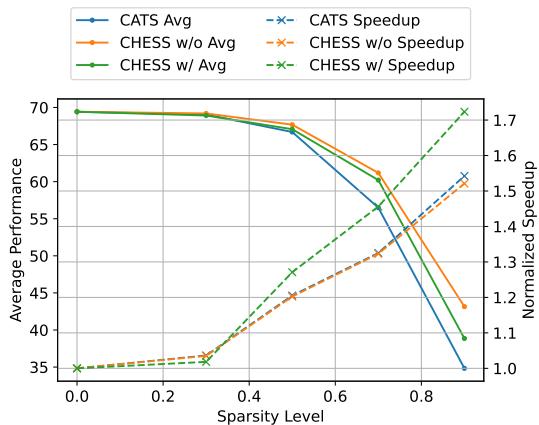
不同稀疏度水平下的下游性能和加速比。

绿线 (CHESS w/) 显示了最佳的权衡。随着稀疏度增加 (在 x 轴上向右移动) ，加速比 (虚线) 直线上升。虽然精度 (实线) 在非常高的稀疏度 (>0.7) 下不可避免地会下降，但 CHESS 保持可用性能的时间比 CATS 长得多。

结论

CHESS 代表了在消费级硬件上部署 LLM 的重要一步。通过摒弃简单的基于幅度的修剪，并重新构想问题以考虑网络层之间的相互作用，研究人员开发出了一种既更快又更智能的方法。

通道级阈值化 (尊重 FFN 通道的独特统计特性) 和选择性稀疏化 (仔细修剪注意力机制的特定部分) 的结合，使得 LLM 可以在不需要昂贵的重新训练的情况下更高效地运行。对于希望在笔记本电脑上运行 Llama-3 的学生和开发人员来说，CHESS 为高效 AI 的未来提供了一个充满希望的蓝图。