像 Claude 3 Sonnet 这样的现代 AI 模型是语言奇才——但在其表象之下隐藏着一个引人入胜的谜团。Anthropic 的研究人员最近在该模型中发现了大约一千二百万个独特的、人类可解释的“特征”。一个特征可以是具体的概念，如“金门大桥”，也可以是抽象的概念，如“用 Python 编写的代码”。令人困惑的是，该模型的神经元数量远少于特征数量。

这种现象——神经网络所表示的特征远多于其神经元数量——被称为 叠加 (superposition) 。 这是大型模型高效运作的关键所在，使它们能够将海量知识压缩进一个相对紧凑的空间。但它也给我们理解这些模型的工作机制带来了挑战——这个研究领域被称为 *机理可解释性 (mechanistic interpretability) *。

迄今为止，大多数研究都集中在模型如何在叠加态下表示或存储特征。但一个关键问题仍未得到解答: 在这些被压缩的特征上进行实际计算时，物理极限是什么？麻省理工学院 (MIT) 最近发表的论文《*关于叠加态中神经计算的复杂性 (On the Complexity of Neural Computation in Superposition) *》正面回答了这一问题。该论文超越了表示层面，首次建立了关于叠加态计算的理论速度极限，揭示了神经网络能够存储与能够计算之间的惊人差距。

理解叠加

在深入讨论论文的发现之前，先澄清几个关键概念。

  • 特征 (Features) : 神经表示的原子构建块。一个特征可能检测到“猫耳朵”，另一个检测“尖锐形状”，第三个检测“毛茸纹理”。它们共同组合，构成“猫”这个概念。
  • 单义神经元与多义神经元 (Monosemantic vs. Polysemantic Neurons) : 在单义表示中，每个神经元对应一个单一特征——清晰但低效。现实中，神经元往往是多义的 (polysemantic) , 同时服务多个特征。
  • 叠加 (Superposition) : 当模型使用的特征多于神经元时，神经元必须同时表示多个特征。每个特征在神经元激活空间中占据一个独特方向。只要这些特征向量近似正交，网络就能成功区分它们。
  • 特征稀疏性 (Feature Sparsity) : 整个机制依赖于假设——对任何给定输入，只有少量特征被激活。缺少稀疏性时，重叠的激活会造成无法控制的噪声。

叠加使像 Claude 3 这样的模型能够存储数百万个不同特征。然而，表示特征与计算特征并不相同。存储压缩信息就像把书存放在档案馆里，而计算更像是同时取出几本书、理解它们的内容，并写出一份新的压缩摘要。后者的难度呈指数级增长。

第一部分: 下界——叠加的硬性限制

为确定理论上可能的范围，作者提出了一个通用框架: 参数驱动算法 (parameter-driven algorithms) 。

想象一台通用机器 \(T\): 给定一组参数 \(P\)，它可以完成任意任务——从排序数字到识别猫。神经架构本身即为 \(T\)；参数 (权重与偏置) 定义了网络所执行的函数。计算复杂性因此取决于这些参数描述的长度。

基于信息论，作者证明: 若网络必须计算 \(m'\) 个元素的所有排列，其参数至少需包含
\(\log_2(m'!) \approx m' \log m'\) 比特。这是因为参数需唯一标识每一个可能函数。更一般地，对于一类逻辑运算——包括 神经置换 (Neural Permutation) 和 2-AND (一组成对的布尔与操作) ——网络必须编码至少
\(\Omega(m' \log m')\) 比特的信息。

假设权重矩阵为方阵，则神经元数量的下界为
\(\Omega(\sqrt{m' \log m'})\)。

关键结果: 要在叠加态中计算 \(m'\) 个特征，至少需要 \(\Omega(\sqrt{m' \log m'})\) 个神经元和 \(\Omega(m' \log m')\) 个参数。

这一结论带来了几个重要洞见:

  1. 计算的基本上限: 一个拥有 \(n\) 个神经元的层最多只能在叠加态中计算 \(O(n^2 / \log n)\) 个特征。这是首次被证明的针对叠加计算的次指数级限制。
  2. 表示与计算的分野: 表示特征的效率可以比计算特征高出指数级。被动存储与主动逻辑之间存在指数级差距 。
  3. 压缩的极限: 量化或剪枝等技术存在硬性底线——压缩超过该界限必然牺牲计算准确性。

第二部分: 上界——构建高效的叠加计算

下界告诉我们不能实现什么，上界则展示我们可以做到的极限。作者提供了一个构造性示例: 一个可证明正确的神经网络，它几乎以最优方式在叠加态下执行多种逻辑运算，仅需
\(O(\sqrt{m' \log m'})\) 个神经元。

步骤 1: 压缩与解压

基础是成对的矩阵——压缩 (compression) 与解压 (decompression) 。 它们负责在稀疏 (单义) 表示与稠密 (叠加) 表示之间转换。

  • 压缩: 稀疏向量 \(\mathbf{y} \in \{0,1\}^m\) 乘以随机矩阵 \(C \in \{0,1\}^{n \times m}\)，生成更短的稠密向量 \(\mathbf{x} = C\mathbf{y}\)。
  • 解压: 通过对 \(C\) 进行转置并归一化构造矩阵 \(D\)，可近似恢复原始稀疏向量: \(\hat{\mathbf{y}} = D\mathbf{x} = DC\mathbf{y} \approx \mathbf{y}\)。

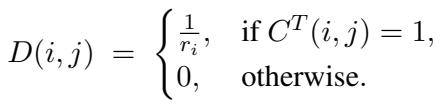
解压矩阵 D 由压缩矩阵 C 的转置构成，并对每一行进行归一化，使其和为 1。

矩阵 \(D\) 逆转压缩过程，确保可从稠密表示中近似恢复稀疏激活。

由于特征具有稀疏性，重建向量在高概率下仍保持准确。该压缩/解压技巧是后续所有构造的关键基础。

步骤 2: 解决神经置换问题

作为简化的热身，研究者展示了如何完全在叠加态中计算一个置换。用矩阵 \(P\) 表示置换，并定义变换矩阵:

\[ T = CPD \]

将其应用于压缩输入 \(\mathbf{x} = C\mathbf{y}\)，得到 \(T\mathbf{x} \approx C(P\mathbf{y})\)，即正确置换后并保持叠加的输出。微小的数值误差可通过基于 ReLU 的阈值化步骤清理。

这证明了逻辑运算可在不解压至原始维度的情况下完成——这是叠加计算可行性的第一个迹象。

步骤 3: 在叠加态下计算 2-AND

论文核心部分展示了如何同时在压缩空间中执行大量成对的与 (AND) 运算，即在稠密表示中实现逻辑计算。

算法的关键是根据新的度量——特征影响力 (feature influence) ——将问题划分为若干子类。影响力定义为一个输入参与多少输出计算。

  • 轻输入 (Light inputs) : 影响力 ≤ \(m'^{1/4}\)。
  • 重输入 (Heavy inputs) : 影响力 > \(m'^{1/4}\)。
  • 输出 (Outputs) : 按输入类型标记为 *双轻量 (double-light) *、*双重量 (double-heavy) * 或 *混合 (mixed) *。

每个类别采用特定策略，但都遵循共享架构: 压缩–计算–解压模块。

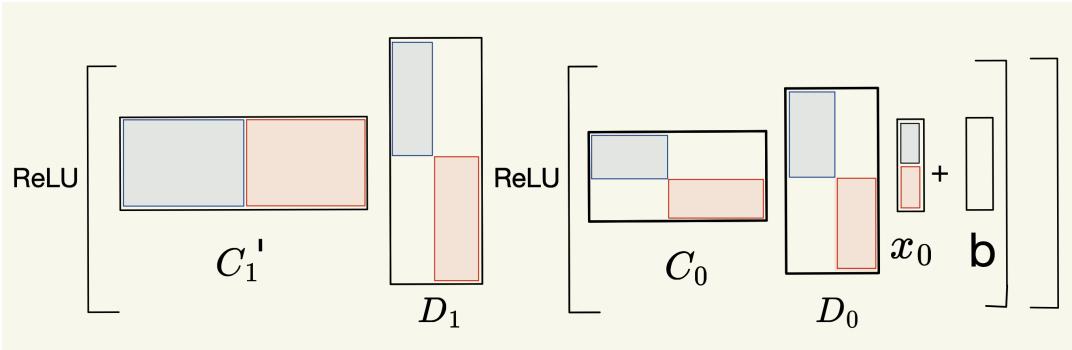
网络矩阵被划分为不同区域。红色和蓝色区域独立计算两个不同的子问题，互不干扰。

独立的矩阵分区保证各子问题互不干扰，从而得到干净的逻辑结果。

情况 1: 双轻量输出

当所有输入均为轻量时，算法使用 输出通道 (output channels) ——为每个输出特征分配随机二进制向量 \(s_i\)。参与输出来的输入共享相同“通道”向量。

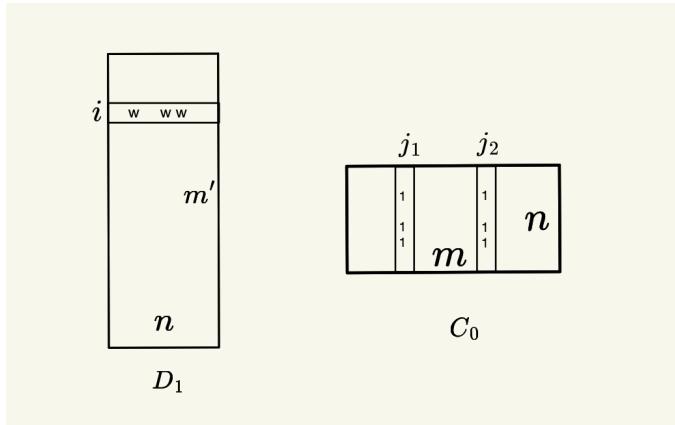
矩阵 C0 和 D1 围绕输出通道设计。对于一个计算 j1 AND j2 的输出 i，C0 的第 j1 和 j2 列被设为相同，使用一个随机向量 s_i。同一向量 s_i 也定义了 D1 中用于输出 i 的解压行。

每个输出通道通过 \(C_0\) 中对齐的列及 \(D_1\) 中对应的行，将正确的输入对路由至目标输出。

流程概述如下:

  1. 使用 \(D_0x_0\) 恢复近似稀疏输入 \(\hat{\mathbf{y}}\)；
  2. 乘以 \(C_0\)，使相关输入对在共享通道位置上重叠；
  3. 减去偏置 -1 并应用 ReLU，保留两个输入均为 1 的激活；
  4. 解压并重新压缩，清除噪声并返回叠加空间。

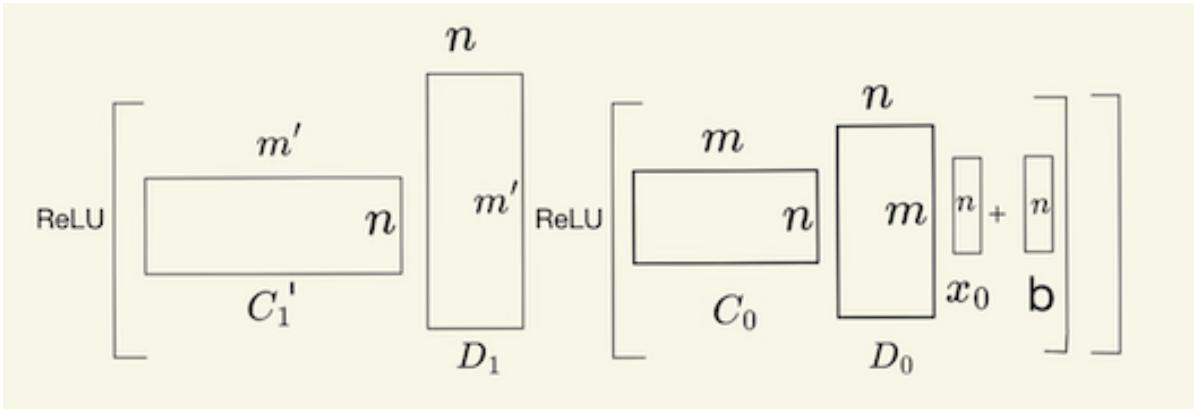
2-AND 问题的完整计算涉及一系列矩阵乘法和 ReLU 激活，有效地对特征表示进行解压、计算和再压缩。

2-AND 计算通过连续的压缩、解压及 ReLU 阶段完成，实现了在压缩空间中的逻辑计算。

这种方法高效且稳定，满足预期的神经元数量限制，并通过阈值步骤有效控制噪声。

情况 2: 重量与混合输出

对于高影响力特征，论文引入 输入通道 (input channels) : 每个高影响力输入获得独立的随机编码，并根据影响力水平采用输入与输出通道结合的混合方案。

混合情况——一个轻输入与一个重输入——需额外机制防止跨通道干扰。最复杂情形是检测两个“超重”输入是否同时激活，并自动取消其组合输出以保持正确性。

尽管这些版本算法复杂，但它们均实现相同的渐近效率:

\[ n = O(\sqrt{m'} \log m') \]

影响与更广泛的意义

该论文的贡献标志着理论与可解释性研究的重要转折点。

  1. 神经效率的基本限制: 一个拥有 \(n\) 个神经元的层仅能计算 \(O(n^2 / \log n)\) 个特征，这为紧凑计算设定了硬性上限。
  2. 表示与计算的指数级差距: 神经元存储特征远比计算特征容易。叠加促进记忆，但不擅逻辑。
  3. 机理可解释性的蓝图: 这些显式算法——尤其是“输出通道”技术——与训练模型中观察到的行为相吻合，为解释已学习电路提供理论框架。
  4. AI 复杂性理论的新领域: 此研究将经典复杂性概念 (如柯尔莫哥洛夫复杂度与信息论下界) 与现代神经计算相结合，为统一的效率与可解释性理论铺路。

研究者在结尾提出开放问题: 这些理论界限能否直接应用于大型语言模型？明确的叠加算法是否能启发出既高效又具可解释性的架构？特征影响力是否能成为现实模型分析中的可测指标？

随着人工智能系统规模不断扩大，理解其基本计算极限将至关重要——不只是为了效率，更为了构建透明、可靠与安全的模型。

简而言之: 叠加让神经网络能用远少于特征数量的神经元表示海量特征——但当要计算这些特征时，数学的现实便显现出来。 你无法欺骗数学: 即使是高度压缩的神经元也有其极限，而如今我们终于知道这些极限在哪里。