是概率还是瞎猜？探究大型语言模型的一致性

大型语言模型 (LLMs) 已成为驱动现代人工智能的引擎，从聊天机器人到代码生成器无处不在。在许多应用中，我们不仅关注模型生成的文本，还关注分数——即模型分配给特定词序列的概率。这些分数被用于检测幻觉、对潜在答案进行排序以及衡量模型的置信度。

但这引出了一个令人不安的问题: 我们真的能把这些数字当作数学概率来信任吗?

在概率论中，一致性是关键。如果你计算两个事件同时发生 (联合概率) 的概率，无论你计算的顺序如何，结果都应该是相同的。然而，近期一篇名为 “CONTESTS: a Framework for Consistency Testing of Span Probabilities in Language Models” 的研究论文揭示，大语言模型往往无法通过这一基本的数学测试。

在这篇文章中，我们将剖析 CONTESTS 框架，探讨为何掩码语言模型 (如 BERT) 和自回归模型 (如 Llama 和 T5) 都在一致性上挣扎，并看看模型规模是如何以令人惊讶的方式影响这些计算的。

核心问题: 顺序本不应影响结果

要理解这个问题，我们需要重温概率的链式法则。

想象一下，你有一个缺失了两个词的句子 (一个跨度) 。假设句子是 “The sky is blue."。要计算单词 “sky” 和 “blue” 出现在这些位置的联合概率，你可以通过两种方式进行:

1. 从左到右: 根据上下文猜 “sky”，然后根据上下文和 “sky” 猜 “blue”。
2. 从右到左: 根据上下文猜 “blue”，然后根据上下文和 “blue” 猜 “sky”。

在数学上，如果 \(P\) 是一个真实的概率分布，这两种计算必须得出完全相同的数值。这是联合分布的一个基本属性。

\[P(sky, blue) = P(sky | context) \times P(blue | sky, context)\]

\[P(sky, blue) = P(blue | context) \times P(sky | blue, context)\]

如果一个语言模型对这两个方程产生不同的值，那么它在概率上是不一致的 。 研究人员着手精确测量现代模型的不一致程度到底有多大。

CONTESTS 框架

作者引入了 CONTESTS (Consistency Testing over Spans，跨度一致性测试) ，这是一个旨在量化这些差异的统计框架。

定义概率顺序

研究人员关注两个相邻 Token \(x_i\) 和 \(x_{i+1}\) 的联合概率。他们定义了模型估算该联合概率的两种不同方式。

第一种方法近似于标准的从左到右的阅读顺序 (或先填充第一个掩码，再填充第二个) :

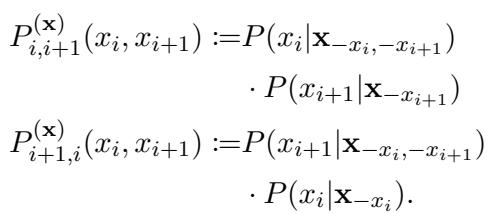
在上图中:

• \(P_{i, i+1}\) 是通过先预测 Token \(i\)，再预测 Token \(i+1\) 计算出的概率。
• \(P_{i+1, i}\) 是通过先预测 Token \(i+1\)，再预测 Token \(i\) 计算出的概率。

在一个完美的世界里，\(P_{i, i+1}\) 和 \(P_{i+1, i}\)应该是完全相同的。

测量差异

为了测量这两个值之间的差别，研究人员定义了一个称为差异度 (discrepancy) 的指标 (\(d\)) 。由于 LLM 中的概率通常是极小的数字，标准做法是在对数空间 (log-space) 中进行操作。差异度定义为两种顺序的对数概率之差:

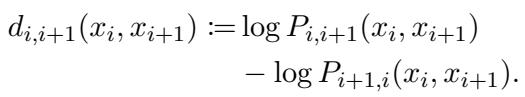
如果一个模型是完全一致的，\(d\) 应该正好是 0。如果 \(d\) 是正数，模型偏好第一种顺序；如果是负数，则偏好第二种。

统计测试

理想情况下，对于一个校准良好的模型，差异度值在许多不同句子上的分布应该以 0 为中心。研究人员使用了 Wilcoxon 符号秩检验来统计确定模型是否存在偏离 0 的偏差。

参赛选手: MLM vs. 自回归模型

该研究对比了两大类大型语言模型:

1. 掩码语言模型 (MLMs) : 如 RoBERTa、XLM-RoBERTa 和 ELECTRA 。 这些模型专门训练用于填充句子中的缺失词 (掩码) 。本质上它们是双向的，能同时看到整个句子。
2. 自回归模型: 如 Flan-T5、Llama 2 和 Llama 2-Chat 。 这些模型通常被训练用于预测序列中的下一个词。为了在“填空”任务上测试它们，研究人员提供了特定的提示 (例如: “Passage: [text with mask]. Answer:”) 。

实验结果: 一致性差距

研究人员在多个数据集上测试了这些模型，包括 Wikitext (模型在训练期间可能见过) 和一个新收集的 News (新闻) 数据集 (在训练截止日期之后) ，以确保公平性。

结果如下图所示，展示了每个模型差异度值 (\(d\)) 的分布。

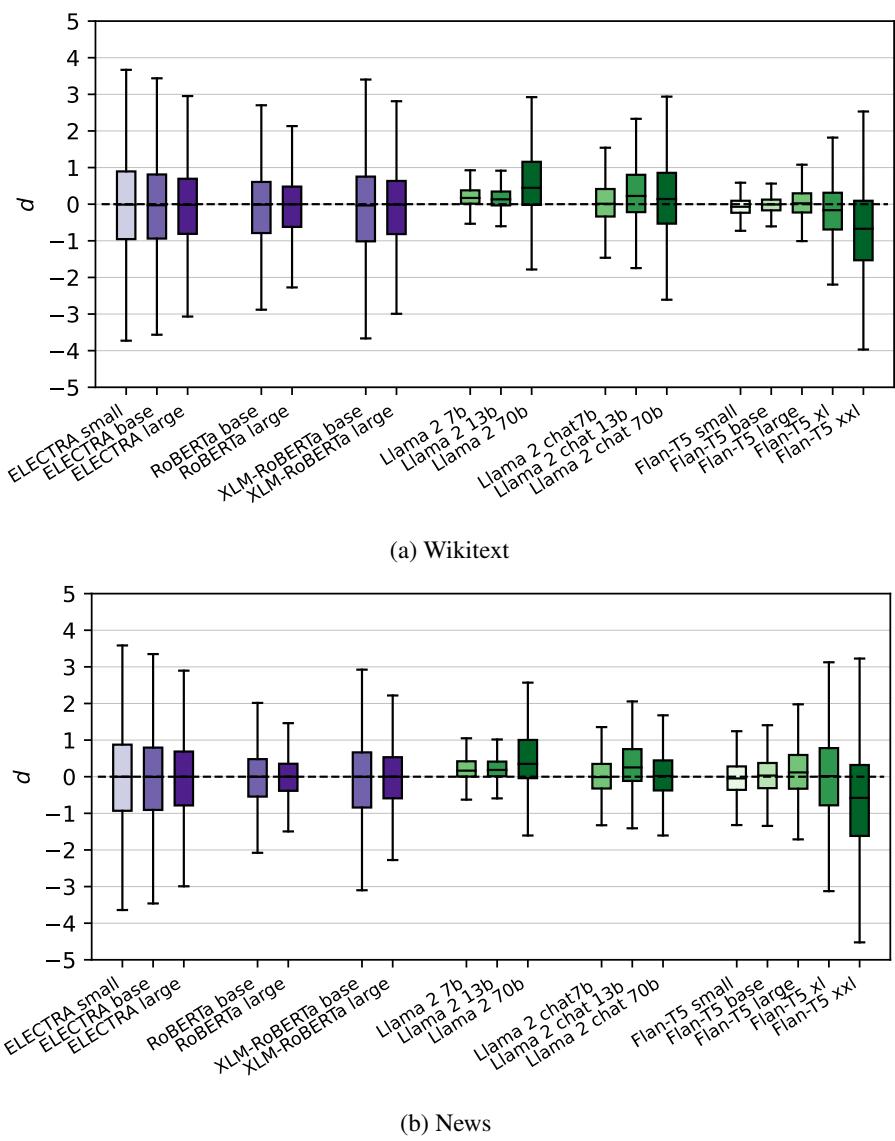
从图 2 中的关键观察:

• 全员不一致: \(d=0\) 的虚线代表完美的一致性。几乎没有模型能严格停留在该线上。统计测试证实，对于几乎所有模型，偏离 0 的情况都具有统计学意义。
• 紫色与绿色的分界: 观察紫色箱体 (MLM) 和绿色箱体 (自回归模型) 的区别。
• MLM 分布更加紧凑且接近 0。它们相对一致。
• 自回归模型 (特别是 Llama 2) 表现出巨大的方差。它们对联合概率的估算会根据解码顺序的不同而剧烈波动。

合成数据压力测试

为了确保这些结果不仅仅是特定自然语言句子的产物，研究人员还使用模板 (例如，"[MASK] [MASK] is a thing”) 生成了一个合成数据集 。 这使他们能够测试模型如何处理低概率、受控的场景。

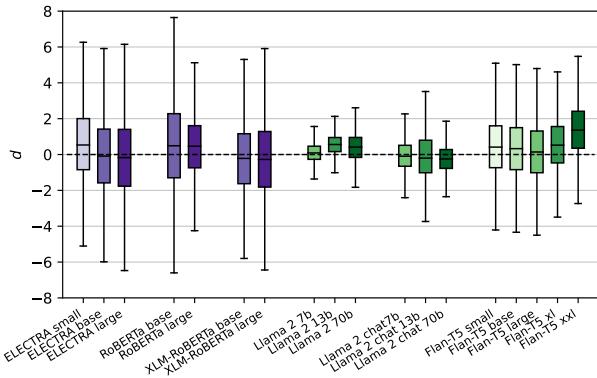
如图 5 所示，这一趋势依然存在，甚至变得更加明显。MLM (左侧) 的差异度进一步偏离零，而自回归模型 (右侧) 继续表现出高方差。

扩展悖论: 越大未必越好

这篇论文最迷人的发现之一是模型规模如何影响一致性。通常我们假设随着参数量的增加 (规模扩大) ，模型在各方面都会变得“更好”。然而，研究人员进行的回归分析表明，在一致性方面并非如此。

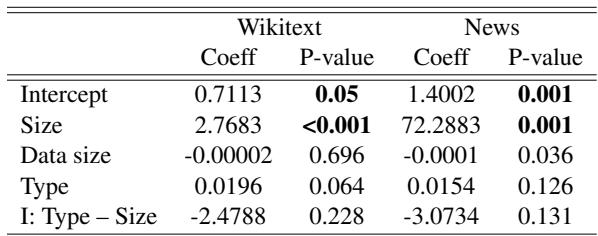
根据表 1，模型规模与差异方差之间存在统计学上的显著关系。但是，这种关系的性质取决于模型架构:

1. MLMs: 随着规模变大，它们的方差倾向于减小 。 它们变得更一致。
2. 自回归模型: 随着规模变大 (例如从 Llama-7b 到 Llama-70b) ，它们的方差增加 。 它们变得更不一致。

这表明，虽然巨大的生成式模型在写文章方面表现惊人，但随着规模的扩大，它们内部的概率计算在涉及计算顺序时可能变得更加不稳定或“偏执”。

仅仅是因为理解不了提示词吗？

一个合理的反驳观点是，自回归模型 (如 Llama) 并非为“填空”任务构建。也许它们不一致只是因为它们不理解被要求做什么？

为了调查这一点，研究人员查看了两个指标:

1. 排名 (Rank) : 模型给正确单词的排名有多高？ (排名越低越好) 。
2. EOS 分数: 模型是否在单词之后立即预测了“句子结束” (End of Sentence) 标记？如果是，说明它理解自己应该只预测一个词。如果否，它可能试图生成整个句子。

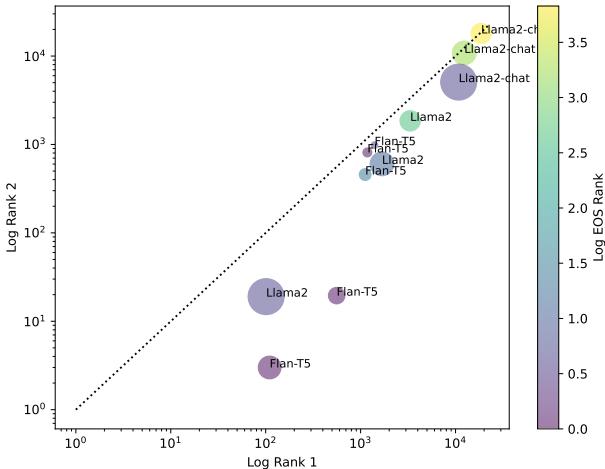
图 7 提供了一个细致的视角:

• X 轴和 Y 轴显示正确单词的排名 (越低/越靠左下越好) 。
• 颜色表示 EOS 排名 (紫色 = 任务理解力好) 。
• 大小表示模型参数量。

我们可以看到 Llama 2-Chat (右上角的大圆圈) 在正确单词的排名上表现不佳，尽管通常具有不错的任务理解力 (紫色) 。相反, Flan-T5 和基础版 Llama 2 模型 (左下角) 很好地理解了任务并能准确排列单词，但我们从之前的图表中知道，它们仍然高度不一致。

这意味着不一致不仅仅是无法理解提示词的副作用；它是模型概率估算的固有特性。

实际意义: 你应该选择哪种顺序？

如果我们知道模型是不一致的——意味着 \(Order A \neq Order B\)——我们能预测哪种顺序“更好” (即为正确答案产生更高的概率分数) 吗？

研究人员发现了熵 (Entropy) (一种不确定性的度量) 与预测顺序准确性之间的联系。

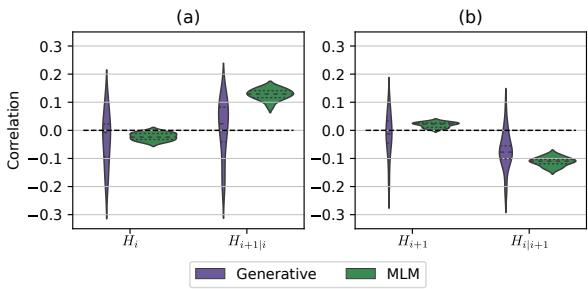
图 4 展示了熵与差异度之间的相关性。关键结论有些反直觉，但具有可操作性:

• 单掩码熵 (\(H_{i+1|i}\)) 呈正相关: 如果模型对它需要填充的第二个词非常不确定 (高熵) ，那么该方向往往会产生更高的概率分数。
• 双掩码熵 (\(H_{i}\)) 呈负相关: 如果模型对第一个词 (当两个都缺失时) 非常不确定，那么该方向往往会产生较低的分数。

策略: 为了最大化真实 Token 的可能性，你应该选择单掩码预测具有较高熵且双掩码预测具有较低熵的解码顺序。

结论

CONTESTS 框架揭示了大型语言模型在处理概率时的根本性“混乱”。虽然我们经常将 LLM 的分数视为严谨的数学概率，但这项研究表明，它们对提问的顺序非常敏感。

• MLM 通常更接近数学上的一致性，特别是随着规模的扩大。
• 自回归模型 (生成式 AI 的当前标准) 的一致性要差得多，而且扩大规模似乎会加剧这个问题。

对于学生和从业者来说，这发出了一个至关重要的警告: 不要将 LLM 的概率分数视为绝对真理。 它们是基于计算方法波动的估算值。然而，通过理解这些不一致性——以及它们与熵的关系——我们可以设计更智能的解码策略，从而充分利用这些强大的模型。

---