想象一下，你要求一个智能助手为三位求职者进行排名: Alice、Bob 和 Charlie。你问助手: “Alice 比 Bob 优秀吗？”它回答是。你问: “Bob 比 Charlie 优秀吗？”它回答是。从逻辑上讲，你会认为如果 Alice 胜过 Bob，而 Bob 胜过 Charlie，那么 Alice 肯定也胜过 Charlie。

但当你问: “Alice 比 Charlie 优秀吗？”助手停顿了一下，然后说: “不，Charlie 比 Alice 更优秀。”

你刚刚遇到了一个逻辑不一致的问题。具体来说，这是违反了传递性 (transitivity) 。

这种情况并非假设。在最先进的大型语言模型 (LLM) 中，这是一个普遍存在的问题。虽然我们经常关注“幻觉” (编造事实) 或“对齐” (拒绝有害请求) ，但存在一个更深层次的结构性问题: LLM 往往缺乏可靠决策所需的基础逻辑一致性。

在研究论文 《与逻辑对齐: 测量、评估和提高大型语言模型中的逻辑偏好一致性》 (Aligning with Logic) 中，研究人员直面了这个问题。他们提出了一个严格的框架来衡量当前模型的不合逻辑程度，并引入了一种名为 REPAIR 的新方法，强制模型进行更一致的思考。

在这篇深度文章中，我们将探索一致性的数学原理，诊断模型失败的原因，并了解我们如何通过数学手段“修复”模型的直觉，使其在逻辑上更加稳健。

LLM 中的逻辑不一致性概述及拟议的 REPAIR 框架。

可靠性危机

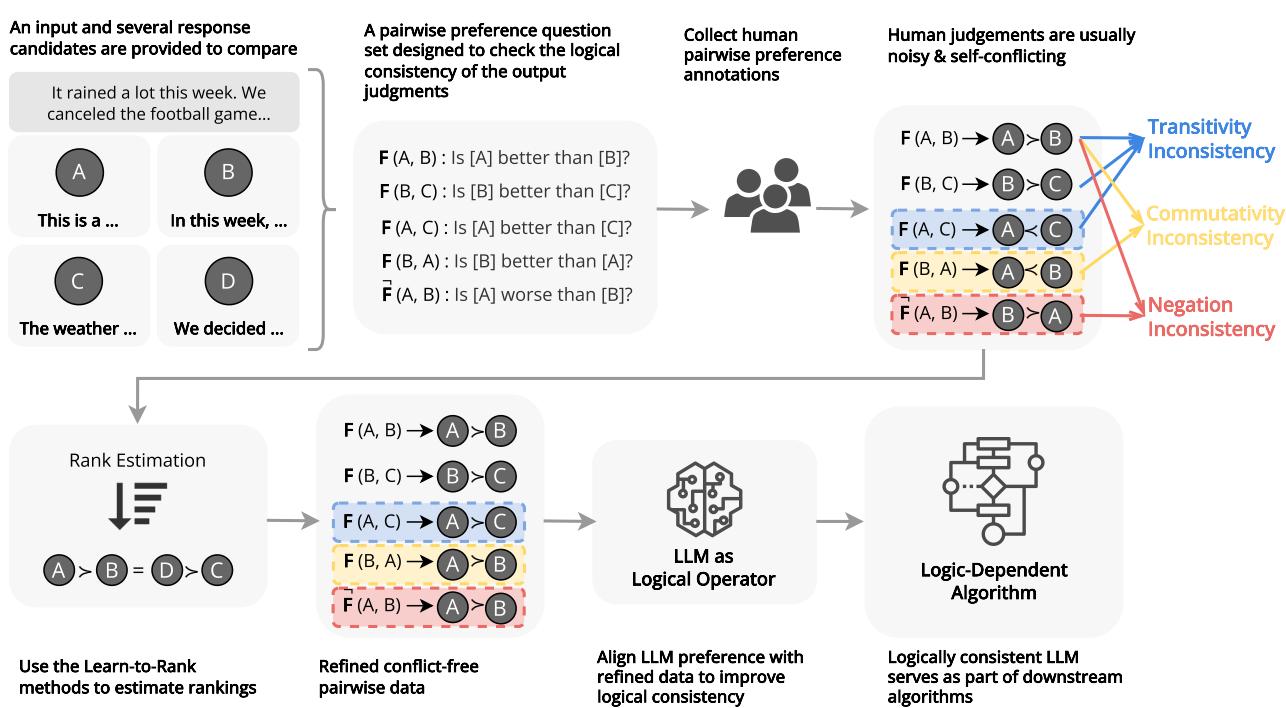
为什么逻辑一致性很重要？如果你只是用 ChatGPT 写一首诗，这可能无关紧要。但 LLM 正越来越多地被用作复杂系统中的算子 (operators) 。 它们被用于重新排序搜索结果、评估代码质量以及对叙事中的时间事件进行排序。

在这些“依赖逻辑”的算法中，LLM 充当一个函数。它接收两个输入并输出一种关系 (例如，\(A > B\)) 。如果这个函数是不稳定的——比如它周二说 \(A > B\)，周三说 \(B > A\)，或者它违反了基本的逻辑规则——整个算法就会崩溃。

研究人员确定了逻辑偏好一致性的三个支柱:

  1. 传递性 (Transitivity) : 推理链必须成立 (\(A > B > C \implies A > C\)) 。
  2. 交换律 (Commutativity) : 输入的顺序不应影响结果 (\(A\) 对 \(B\) 的结果应与 \(B\) 对 \(A\) 相同) 。
  3. 否定不变性 (Negation Invariance) : “A 比 B 好”在语义上必须等同于“B 比 A 差”。

让我们逐一分解，看看论文是如何量化它们的。

第一部分: 测量疯狂

要治疗病人，我们首先需要诊断疾病。研究人员将 LLM 视为一个算子函数 \(F(x_i, x_j)\)，它比较两个项目并输出一个决策。

1. 传递性: 混乱的循环

传递性是排名的基石。没有它，你就无法对列表进行排序。如果一个 LLM 认为 A 优于 B，B 优于 C，而 C 又优于 A，它就创造了一个循环 (cycle) 。 在图论中，一组完全一致的偏好会形成一个有向无环图 (DAG) ——即没有循环的图。

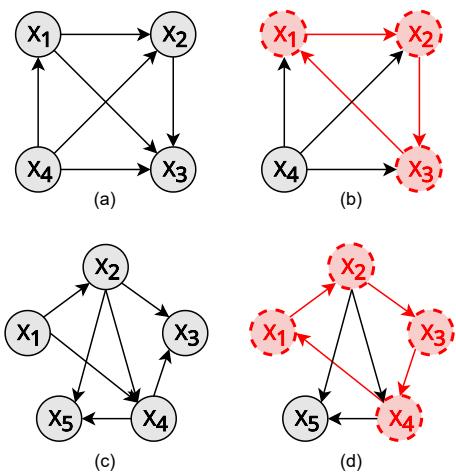
展示传递关系与循环违例的图示示例。

如图 2 所示，传递关系看起来像一个层级结构 (图 a、b、c) 。违例看起来像一个循环 (图 d) 。研究人员提出了一个指标 \(s_{tran}(K)\) 来衡量这一点。

由于计算大型数据集中所有可能的项目组合在计算上是不可能的 (组合数量呈指数爆炸) ，他们对大小为 \(K\) 的子图 (例如，3 或 5 个项目的子集) 进行采样。

该指标定义为一个大小为 \(K\) 的随机子图不包含循环的概率:

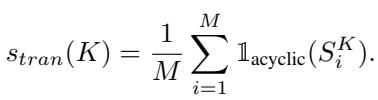
计算传递性分数的公式。

这里，\(\mathbb{1}_{\mathrm{acyclic}}\) 是一个函数，如果子图是一个有效的层级结构 (无循环) 则返回 1，如果包含矛盾则返回 0。分数为 1.0 意味着模型在推理上是完全分层的。较低的分数表明模型处于混乱状态。

2. 交换律: “首位即最佳”偏差

LLM 有一种众所周知的心理怪癖: 位置偏差 (positional bias) 。 它们通常更喜欢展示给它们的第一个选项，有时是第二个，而不管内容如何。

交换律要求 \(F(A, B)\) 产生与 \(F(B, A)\) 相同的逻辑结果。如果当 A 排在第一位时模型说“选项 A 更好”，那么当 B 排在第一位时，它应该说“选项 B 更差” (这暗示 A 更好) 。如果仅仅因为你交换了顺序它就改变了主意，那它就缺乏交换性。

研究人员在图 3 (左侧矩阵) 中将其可视化。红圈显示了模型的判断因位置而发生翻转的冲突。

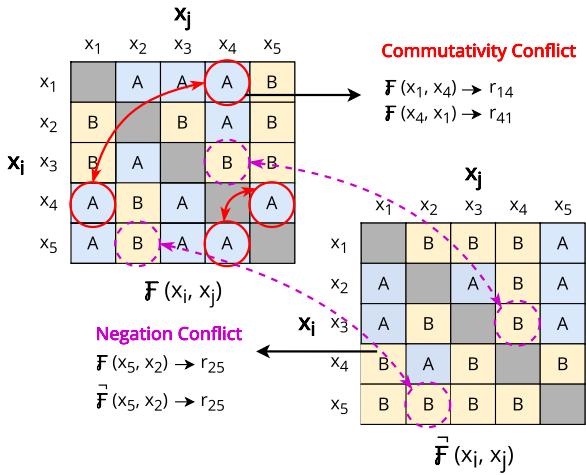
说明交换律和否定冲突的矩阵。

他们将交换律分数 \(s_{comm}\) 定义为模型无论顺序如何都保持一致判断的配对百分比:

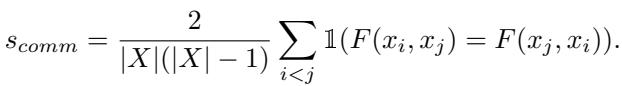
交换律分数的公式。

3. 否定不变性: 理解“不”

这是一个语言逻辑检查。如果我问，“A 比 B 好吗？”你说“是”，那么如果我问，“A 比 B 差吗？”，你必须说“不”。

令人惊讶的是，LLM 在这方面很吃力。它们可能同意 A 比 B 好，但如果以不同的方式提示，它们也可能同意 A 比 B 差。通过检查模型对标准问题的判断是否与对否定问题的判断的逻辑否定相匹配，来衡量这一属性。

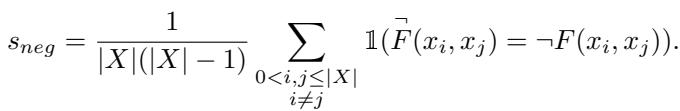
否定不变性分数的公式。

为了测试这一点，研究人员使用了提示模板，明确要求模型判断“更好”与“更差”，如下所示:

用于测试否定不变性的提示模板。

第二部分: 诊断 (实验结果)

研究人员在三个不同的任务上对流行模型 (Llama-2、Llama-3、Mistral、GPT-3.5) 进行了这些测试:

  1. SummEval: 判断两个文本摘要中哪一个更连贯。
  2. NovelEval: 判断两个文档中哪一个与查询更相关。
  3. CaTeRS: 确定事件的时间顺序 (事件 A 是否发生在事件 B 之前？) 。

结果总结在表 1 中，揭示了一些引人入胜的模式。

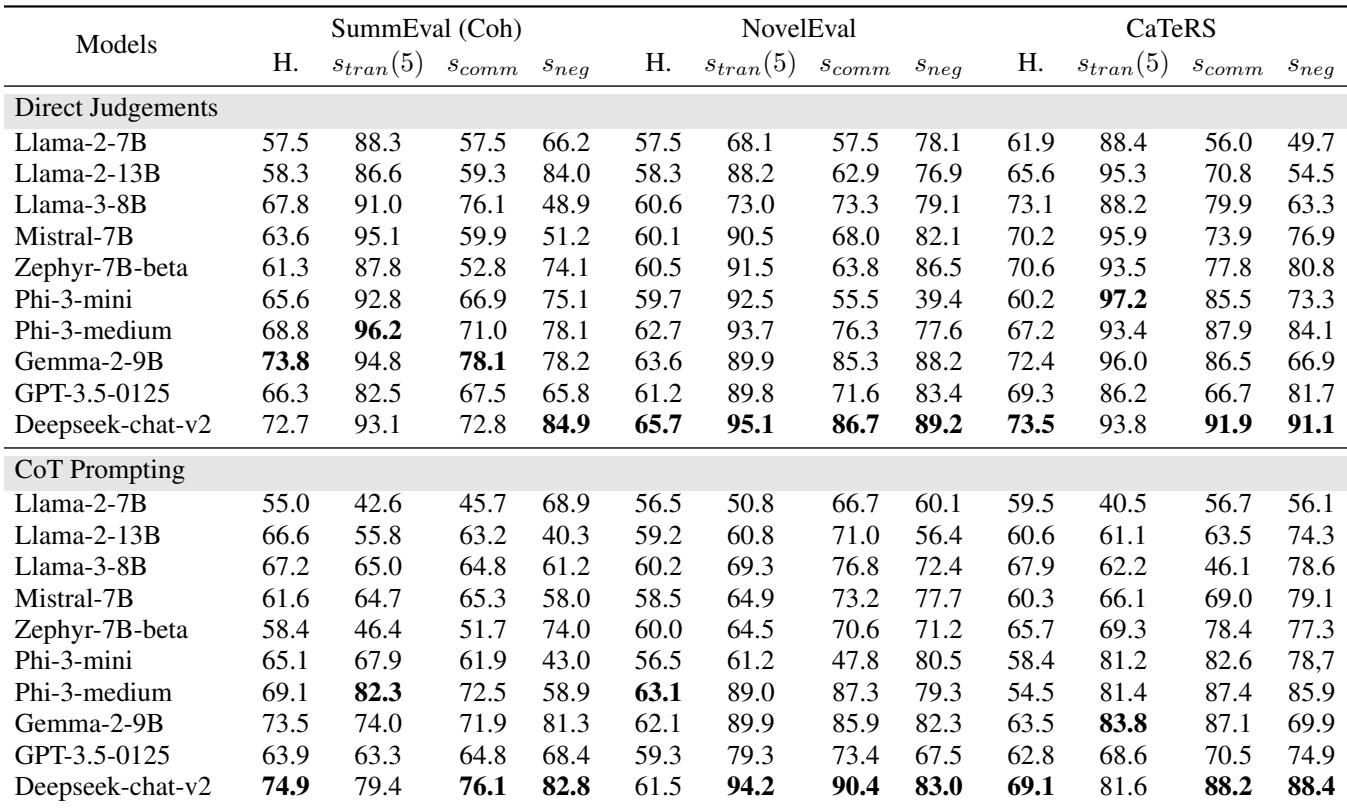
显示各模型逻辑一致性分数的表格。

诊断的关键要点:

  1. 越新 (大多) 越好: 像 Phi-3-medium 和 Gemma-2-9B 这样的较新模型显示出比 Llama-2 等旧模型高得多的一致性。
  2. 传递性很难: 虽然有些模型得分很高 (90%+) ，但其他模型难以在多个项目间保持连贯的世界观。
  3. 主观性损害逻辑: 模型通常在 CaTeRS (时间排序) 上的表现优于 SummEval。为什么？因为时间是客观的。事件 A 物理上发生在事件 B 之前。摘要质量是主观的，导致模型更多地“摇摆不定”，产生不一致。
  4. 思维链 (CoT) 可能会适得其反: 这是一个违反直觉的发现。我们通常假设 CoT (要求模型“一步步思考”) 能改善一切。然而，研究人员发现 CoT 有时会降低传递性。
  • *理论: * 当模型生成长思维链时，它引入了更多的 token，并可能在其推理过程中引入更多的“随机性”。它在处理配对 A 与 B 时使用的逻辑可能与处理配对 B 与 C 时略有不同，从而导致循环。

一致性 = 可信度

研究人员还发现，模型的逻辑一致性与其自洽性 (Self-Agreement) (如果你多次问同一个问题，它给出相同答案的频率) 之间存在很强的相关性。

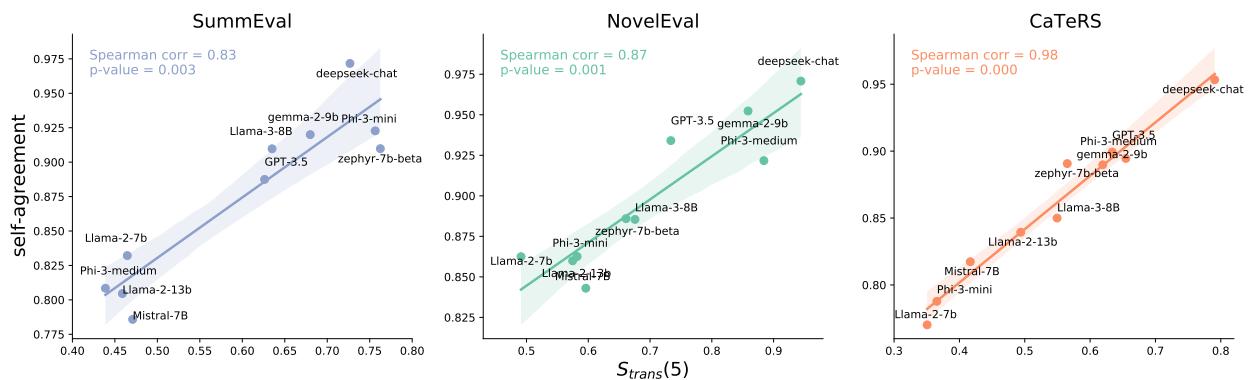
显示传递性与自洽性之间相关性的散点图。

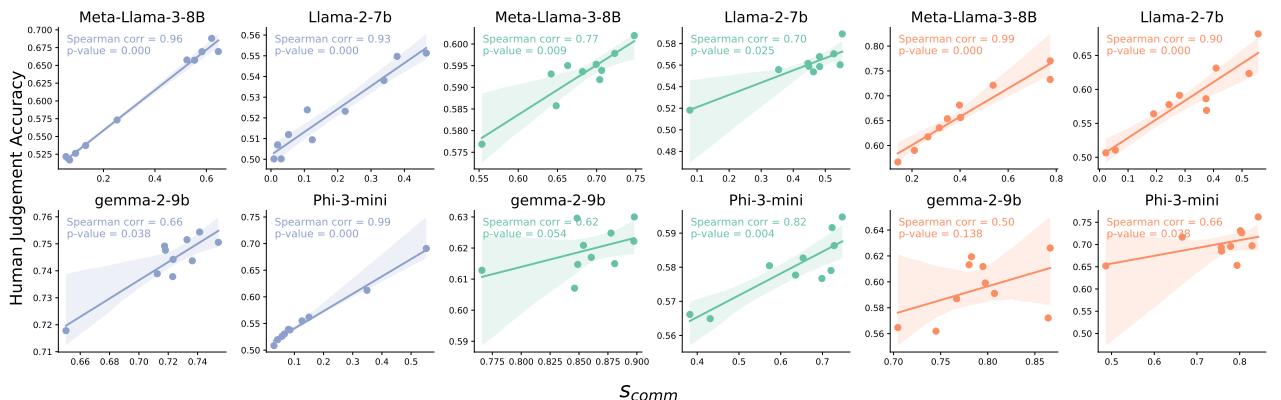
如图 4 所示，传递性高 (x 轴) 的模型也是不会随机改变答案的模型 (y 轴) 。这表明测量逻辑一致性是衡量整体模型可靠性的绝佳代理指标。

此外, 交换律与人类偏好准确性之间存在密切联系。不受选项顺序左右的模型往往能更好地与人类判断保持一致。

显示交换律与人类偏好准确性之间相关性的散点图。

第三部分: 疗法 - REPAIR 框架

那么，我们的模型在逻辑上存在缺陷。我们要如何修复它们？

你可能会想: “只要在更多人类数据上训练它们就行了！”

问题在于人类也是不一致的 。 人类标注数据集充满了噪音、错误和主观矛盾。如果你在一个标注者 1 说 A>B 而标注者 2 说 B>A 的数据集上训练 LLM，模型学到的就是困惑。

研究人员介绍了 REPAIR (通过信息提炼进行排名估计和偏好增强，Ranking Estimation and Preference Augmentation through Information Refinement) 。

REPAIR 流程

核心思想是在向模型展示之前，获取嘈杂、矛盾的成对数据，并将其“净化”为数学上一致的排名。

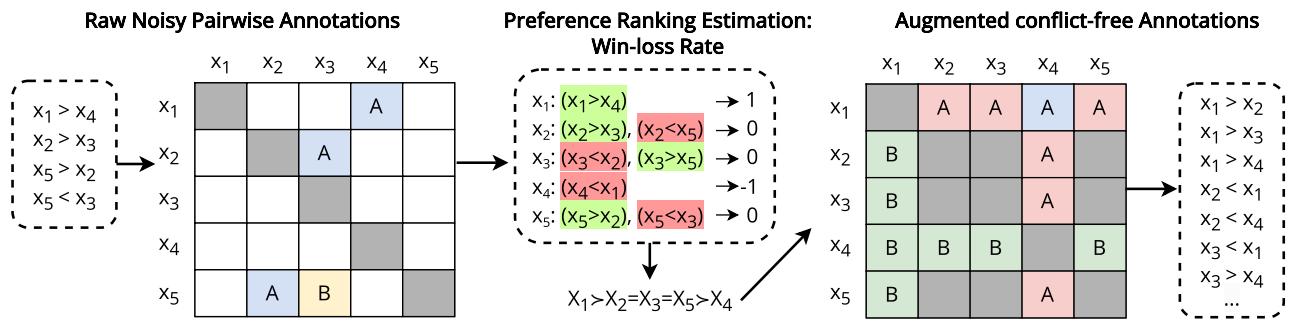
REPAIR 数据提炼过程图解。

这是图 6 中展示的逐步过程:

  1. 输入: 原始、嘈杂的成对标注 (例如，“A 比 B 好”，“B 比 C 好”，“C 比 A 好”) 。
  2. 估计 (胜负率) : 系统着眼于全局。它根据每个项目在整个数据集中赢得比较的次数来计算分数。
  • 如果 A 击败 B，A 得分。
  • 如果 C 击败 A，A 失分。
  • 最终，出现一个全局排名: \(X_1 = X_2 = X_3 = X_5 > X_4\)。
  1. 线性化: 系统根据这些分数将项目强制排列成一个列表。这消除了循环。在一个编号的列表中不可能存在剪刀石头布式的循环。
  2. 增强: 系统根据这个干净的列表生成新的成对比较。它暗示了原始数据中不存在的关系。如果列表显示 \(A > B > C\)，系统会创建一个训练示例 \(A > C\)，即人类从未明确比较过 A 和 C。
  3. 指令微调: LLM 在这个新的、逻辑完美的数据集上进行微调。

为什么要用胜负率？

论文讨论了不同的项目排名方法 (如 Elo 等级分或 Bradley-Terry 模型) 。然而，他们选择了简单的胜负率 (Win-Loss Rate) 。 为什么？因为它对稀疏数据 (我们没有每一对的比较数据) 具有鲁棒性，并且不像其他方法那样受比较处理顺序的影响。

通过增强数据，他们还大幅增加了训练集的大小，如表 2 所示。

REPAIR 增强前后的数据集大小统计。

第四部分: REPAIR 有效吗？

研究人员通过微调 Llama-3-8B 测试了 REPAIR。他们比较了三个版本:

  1. 零样本 (Zero-shot) : 基础模型。
  2. 扰动数据 (Perturbed Data) : 在原始、嘈杂的数据上训练 (模拟标准做法) 。
  3. REPAIR-ed 数据: 在经过数学清洗的数据上训练。

结果是具有变革性的。

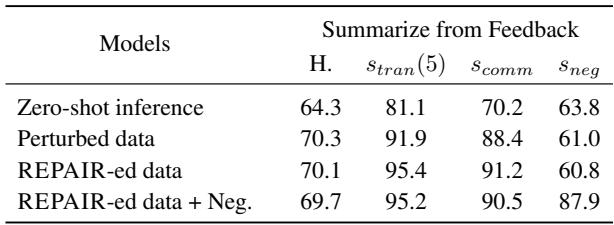
表格显示使用 REPAIR 后一致性的提升。

观察表 3 , REPAIR-ed 模型在传递性和交换律上达到了近乎完美的分数 (1.0 或 100%) 。

至关重要的是, 人类对齐 (H.) 并没有下降。通常在 AI 中存在一种权衡: 你可以让模型更有逻辑，但它会变得僵化，不太像“人类”。在这里，模型变得完全符合逻辑，同时保持 (甚至略微提高) 了它们与人类偏好的一致性。

*关于否定不变性的注记: * 为了修复否定一致性 (理解“更差”与“更好”) ，研究人员必须在训练数据中明确包含否定示例 (“REPAIR-ed data + Neg.”一行) 。这将否定分数从 60.8% 提升到了 87.9%。

对现实世界算法的影响

最后，研究人员问: “这真的有助于我们要做的排序工作吗？”

他们使用了一种名为 PairS 的算法，该算法使用 LLM 对项目列表进行排序 (就像冒泡排序或归并排序) 。标准的 LLM 在这方面很吃力，因为如果它们不具备传递性 (\(A>B, B>C, C>A\)) ，排序算法就会陷入循环或产生错误的顺序。

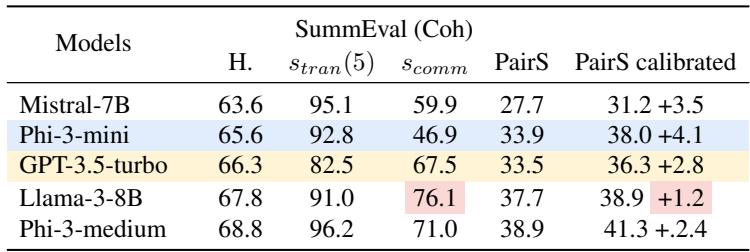
表格显示在 PairS 排序算法上的表现。

表 4 证明，具有较高传递性的模型 (如 REPAIR-ed 模型) 在排序任务上表现明显更好。

这里有一个关于校准 (calibration) 的有趣发现。通常，工程师必须运行“校准”流程 (询问模型两次，先 A-B 然后 B-A) 以平均偏差。这使推理的成本和时间加倍。结果表明，具有高交换性的模型 (那些由 REPAIR 修复的模型) 不需要这种校准。它们第一次就能得到正确的答案，使其效率提高了一倍 。

结论

大型语言模型的“黑盒”性质通常让它们在逻辑上获得了豁免权。我们对它们的文采印象深刻，而忽视了它们的推理缺陷。但随着我们从将 LLM 用作聊天机器人转变为将其用作决策智能体，逻辑一致性变得不可协商。

这篇论文为这种转变提供了路线图。它教给我们三个主要教训:

  1. 测量是可行的: 我们可以使用传递性、交换律和否定不变性来数学量化模型的“困惑”程度。
  2. 人类数据是瓶颈: 直接在嘈杂的人类反馈上训练会教会模型不一致性。
  3. 逻辑是可以诱导的: 通过使用像 REPAIR 这样的排名算法提炼数据，我们可以创建强制模型遵守逻辑法则的训练集，而无需牺牲它们与人类意图的对齐。

可靠 AI 的未来不仅仅关于更大的模型；它关乎不自相矛盾的模型。有了像 REPAIR 这样的框架，我们离逻辑——而不仅仅是语言——可以依赖的 AI 又近了一步。