如果你玩过 Word2Vec 或早期的语言模型，你可能对 NLP 中那个著名的代数奇迹并不陌生: King - Man + Woman = Queen。这种向量运算表明，语言模型 (LM) 不仅仅是在死记硬背文本；它们隐式地学习了语义和句法结构。

然而，要显式地提取这种结构——即绘制出句子的实际语法树——通常需要在昂贵的手工标注数据集 (如 Penn Treebank) 上进行监督训练。但是，如果我们能让预训练的大型语言模型 (LLM) 在没见过任何标注解析树的情况下，吐露其语法知识呢？

在论文 “On Eliciting Syntax from Language Models via Hashing” 中，来自日本国家信息通信研究机构 (NICT) 的研究人员提出了一种名为 Parserker2 的迷人方法。通过结合经典的动态规划算法 (CKY) 与现代对比学习和二进制哈希技术，他们成功地从原始文本中诱导出了高质量的句法树。

这篇文章将带你了解他们如何将解析机制从“零阶”升级为“一阶”，如何将解析转化为哈希问题，以及使无监督学习变得稳定所需的巧妙损失函数。

核心问题: 语法在哪里？

语法是语言的隐形骨架。在像 “The quick brown fox jumps” 这样的句子中，我们要知道 “The quick brown fox” 构成了一个名词短语 (NP) ，而 “jumps” 充当动词 (V) 。 成分句法分析器 (Constituency Parser) 的目标就是恢复这种层次化的树状结构。

标准方法通常遵循这样的流程:

  1. 获取一个句子。
  2. 用模型 (如 BERT) 对其进行编码。
  3. 在数千个标记好的树上训练分类器，以预测哪些单词应该组合在一起。

研究人员提出了一个更难的问题: 我们能否仅利用原始文本和预训练模型的内部知识来诱导出这些树?

为此，他们依赖一种称为 二进制表示 (Binary Representation) 的技术。模型不再是从固定列表中预测“NP”或“VP”这样的标签，而是为每个文本跨度 (span) 预测一个二进制代码 (例如 10110...) 。如果两个跨度在语法上相似，它们应该具有相似的二进制代码。

架构概览

在深入数学细节之前，让我们先看看高层架构。

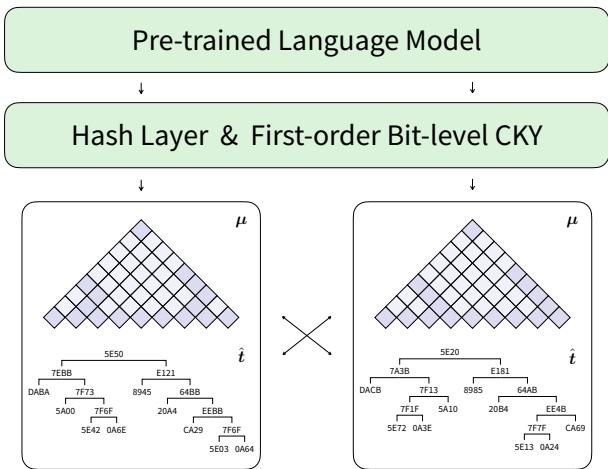
图 1: 模型架构。哈希层生成所有跨度的分数，随后的一阶比特级 CKY 返回边缘概率并预测最可能的树。

该模型接收一个句子，并将其传递给预训练的 LM (如 BERT) 。然后，它使用一个 哈希层 (Hash Layer) 生成分数，这些分数被输入到 比特级 CKY (Bit-level CKY) 模块中。输出是一棵解析树，其中每个节点都标有十六进制哈希码，而不是语言学标签。

背景: 零阶解析的局限性

要理解这里的创新，我们需要重温 CKY (Cocke-Kasami-Younger) 算法。CKY 是一种自底向上的解析算法，用于查找句子最可能的树结构。它的工作原理是将较小的文本跨度组合成较大的跨度。

在之前的研究 (Parserker1) 中，作者使用了 零阶 CKY (Zero-order CKY) 。 在这种设置中，一个跨度 (例如短语 “the lazy dog”) 的分数仅取决于边界标记: 开头 (“the”) 和结尾 (“dog”) 。

\[ g(l,r,c) = \dots \text{function of } h_l \text{ and } h_r \]

虽然计算效率高，但这在语言学上是薄弱的。一个短语的语法角色不仅仅由其边缘决定；它取决于其内部结构。因为零阶解析忽略了“分割点” (即短语分裂成子节点的位置) ，所以它很难在无监督设置下学习复杂的语法。

解决方案: 一阶比特级 CKY

作者引入了 一阶 CKY (First-order CKY) 。 在这个升级版本中，跨度的分数取决于 分裂位置 (\(m\)) 。

想象一下解析短语 “The quick brown fox”。

  • 零阶 会问: “The” 和 “fox” 看起来像是一个有效短语的边缘吗？
  • 一阶 会问: 如果我们在这里把 “brown” 分开 (The quick brown | fox) ，左子节点 (“The quick brown”) 和右子节点 (“fox”) 的组合说得通吗？

通过结合分割点 \(m\)，模型将词汇信息 (单词) 和句法信息 (它们如何组合) 统一到了一个单一的表示中。

可视化差异

这种差异在动态规划图表 (用于计算解析概率的网格) 中最容易看出:

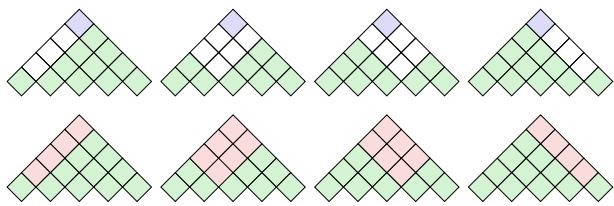
图 2: 零阶 (上) 和一阶解析 (下) 的图表。

在顶部的三角形 (零阶) 中，预测依赖于最顶端的单元格。在底部的三角形 (一阶) 中，预测是由交叉左子节点和右子节点的单元格平均后做出的联合决策。

“平均化”技巧

你可能会担心检查每个可能的分割点太慢了。如果我们必须为每个 \(m\) 计算复杂的神经网络操作，系统将变得不可用。

研究人员发现了一个巧妙的数学捷径。他们不再为每个分割计算新的向量，而是简单地 平均 组成部分的分数。

\[ \begin{array} { c } { \displaystyle { g ( l , r , m , c ) = \sum _ { k = 1 } ^ { K } g _ { k } ( l , r , m , c ^ { k } ) } } \\ { \displaystyle { g _ { k } ( l , r , m , + 1 ) = \frac { ( \mathbf { W } _ { k } ^ { Q } \overline { { h } } _ { l : m } ) ^ { \top } ( \mathbf { W } _ { k } ^ { K } \overline { { h } } _ { m + 1 : r } ) } { \sqrt { d _ { k } } } } } \\ { \displaystyle { \overline { { h } } _ { l : m } = \operatorname* { m e a n } _ { l \leq i \leq m } h _ { i } } } \\ { \displaystyle { \overline { { h } } _ { m + 1 : r } = \operatorname* { m e a n } _ { m < j \leq r } h _ { j } } } \end{array} \]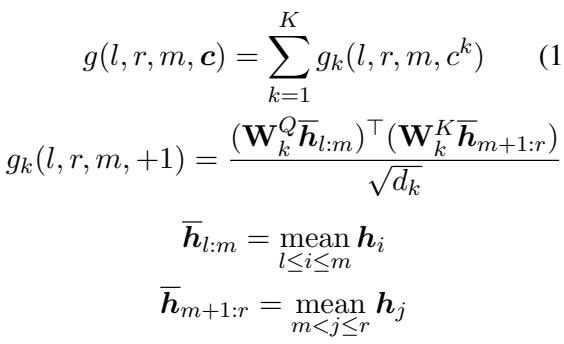

描述使用均值向量的一阶评分机制的方程。

这个方程本质上是说: 要获得从 \(l\) 到 \(m\) 跨度的表示，只需取该范围内隐藏状态的平均值 (\(\overline{h}_{l:m}\)) 。这使得模型能够捕捉短语的“重心”，使解析对内部结构敏感，而不会导致计算成本激增。

对于特定比特 \(k\) 为 \(+1\) 的计算，可以完美简化为对子组件分数的平均:

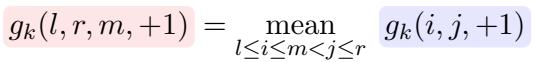
方程 19 展示了简化的均值计算。

通过对比哈希进行无监督训练

现在我们有了一个构建树的机制 (一阶 CKY) 。但我们如何在没有标签的情况下训练它呢？我们不知道一个跨度是 NP 还是 VP。

答案是 对比学习 (Contrastive Learning) 。

直觉很简单: 相同的短语应该具有相同的哈希码。

如果短语 “the lazy dog” 出现在句子 A 中，又出现在句子 B 中，模型应该给它们分配相同的二进制代码 (例如 1101) ，而不管上下文如何。相反，“the lazy dog” 的代码应该与 “jumps over” 不同。

定义正样本和负样本

模型将解析任务视为一个自监督问题。

  1. 正样本集 (\(\mathcal{P}\)) : 具有完全相同文本内容的跨度 (\(w_{\hat{l}_i:\hat{r}_i} = w_{\hat{l}_j:\hat{r}_j}\)) 。
  2. 负样本集 (\(\mathcal{N}\)) : 具有不同文本内容的跨度。

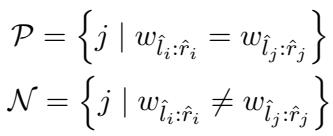
基于单词一致性定义正负样本集的方程。

模型不再为每个可能的短语维护一个巨大的嵌入表 (那将有数百万个条目) ，而是使用 对比哈希 。 它将正样本对的二进制代码拉近，将负样本对推远。这将“这是什么标签？”的问题转化为“这两个是一样的吗？”的问题，这在没有监督的情况下更容易学习。

生成二进制代码

跨度的二进制代码 \(\mathbf{c}\) 不是任意的。它是从 CKY 算法计算出的 边缘概率 派生出来的。如果比特 \(k\) 为 \(+1\) 的概率高于 \(-1\)，则该代码位变为 \(+1\)。

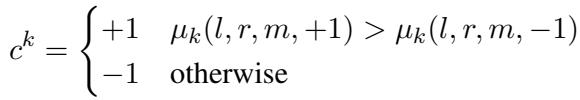
展示如何从边缘概率派生二进制代码的方程。

损失函数之战

这篇论文最技术性的贡献——也是这种方法之所以有效而其他方法失败的原因——在于损失函数的设计。

在标准的对比学习 (如 SimCSE) 中，通常有一个正例和许多负例。但在解析中，像 “the” 这样的常见短语可能会在一个批次中出现几十次。你会有 多个正例 。

如果你只取到所有正例的平均距离，模型会感到困惑 (即“几何中心”问题) 。如果你只看最近的正例，对于像语言这样大的输出空间来说，信号又太弱了。

提议的解决方案: \(\ell_{\overline{\min}}\)

研究人员建议关注 最难 的情况。他们希望最小化到 最远 正例的距离 (使聚类紧凑) ，同时最大化到负例的距离。

然而，简单地使用 min/max 算子会使训练变得不稳定，因为梯度会被正项主导。为了解决这个问题，他们引入了一个 平衡损失函数 , 称为 \(\ell_{\overline{\min}}\)。

\[ \ell _ { \overline { { \mathrm { min } } } } \approx \operatorname* { m a x } _ { \mathcal { N } \cup \{ \overline { { \mathrm { min } } } _ { \mathcal { P } } \} } s ( i , j ) - \operatorname* { m i n } _ { \mathcal { P } } s ( i , j ) \]

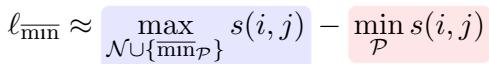
平衡损失函数方程。

详细分解如下:

  1. \(\min_{\mathcal{P}}\) (拉力) : 这一项关注“最差”的正匹配 (距离最远的那个) 并试图将其拉近。这提供了强大的对齐信号。
  2. \(\overline{\min}_{\mathcal{P}}\) (平衡) : 这一项被添加到负样本侧。它是最小算子的“软”版本 (使用 LogSumExp) 。它确保来自正项的梯度不会压倒来自负项的梯度。

这种平衡防止了模型坍缩成平凡解 (如右分支树) ，并迫使它学习有意义的结构。

实验与结果

它真的有效吗？研究人员在 Penn Treebank (英语) 和 Chinese Treebank (中文) 上测试了 Parserker2。

英语结果 (PTB)

在 Penn Treebank 上，与其它无监督方法相比，该模型实现了具有竞争力的 F1 分数。

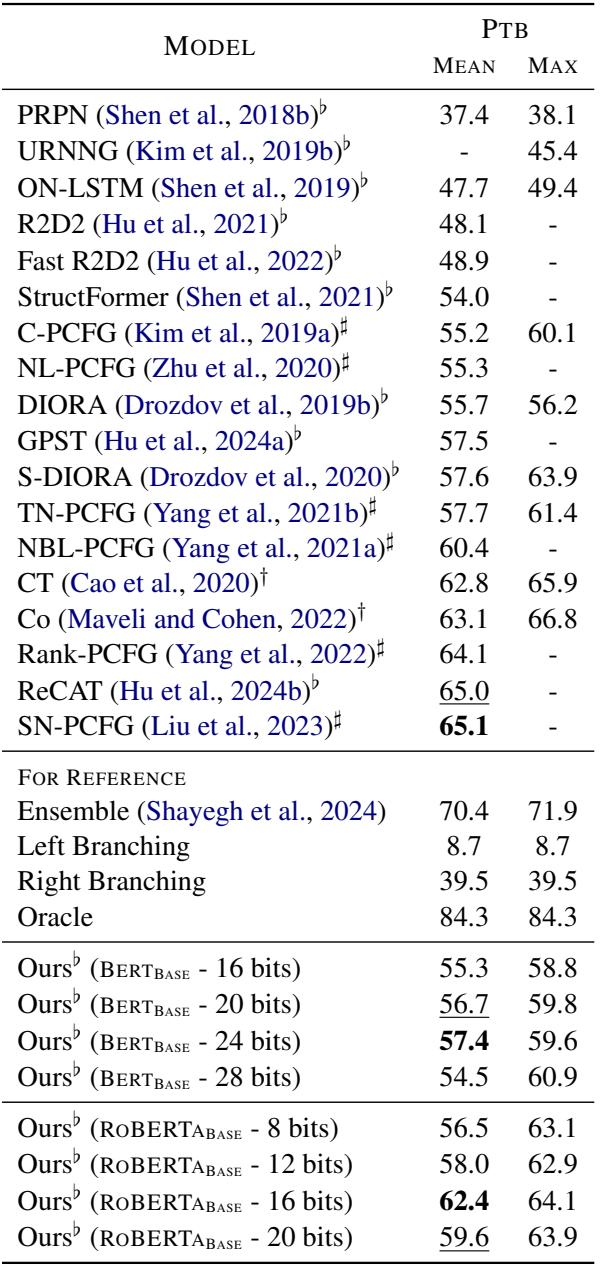
表 1: PTB 数据集上的无监督成分解析实验。

如表 1 所示，“Ours” (Parserker2) 始终优于隐式语法模型 (如 ON-LSTM 和 PRPN) 。它在使用 BERT-Base 和 24 位哈希时实现了 57.4 的 F1 分数，考虑到它没有使用任何标记数据，这是令人印象深刻的。

中文结果 (CTB)

在中文上的结果更加引人注目。对于无监督模型来说，中文句法通常也是出了名的难。

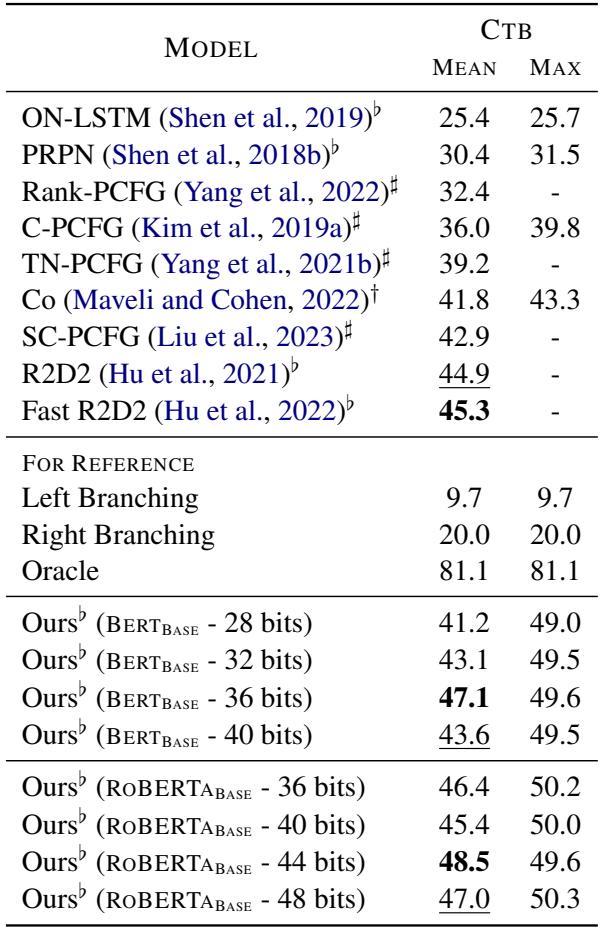
表 2: CTB 数据集上的无监督成分解析实验。

表 2 显示，Parserker2 显著优于几乎所有基线模型。有趣的是，与英语相比，该模型在中文上需要更多的位数 (36-44 位) 才能达到峰值性能，这表明捕捉中文句法需要更高维度的二进制空间。

深入矩阵: 树长什么样？

数字很好看，但可视化效果更好。由于模型输出带有十六进制标签的树，我们可以将它们与真实树进行比较。

以句子为例: “The quick brown fox jumps over the lazy dog.”

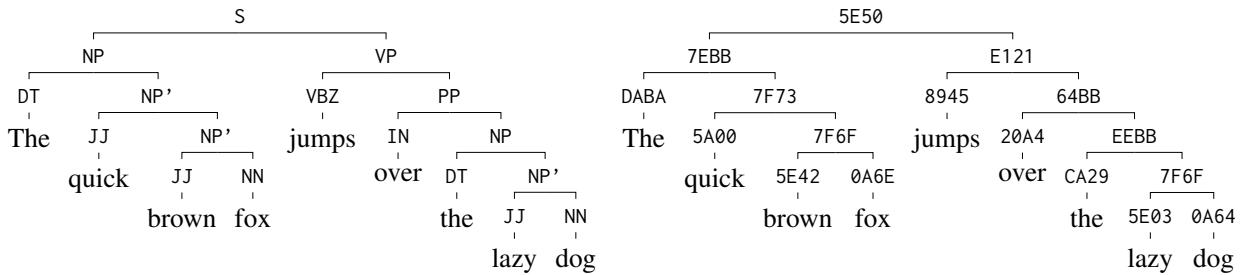
图 3: 句子 “The quick brown fox jumps over the lazy dog” 的推导过程。基准真相与模型输出的对比。

在上图中:

  • 左侧: 带有 NP (名词短语) 和 VP (动词短语) 等标签的人工标注树。
  • 右侧: 带有十六进制代码的模型输出。

请注意，结构是 相同 的。

  • 模型正确地将 “The quick brown fox” 归为一个节点 (7EBB) 。
  • 它将 “the lazy dog” 归为另一个节点 (EEBB) 。
  • 关键是，相似概念的代码也是相似的。像 “quick” (5A00) 和 “brown” (5E42) 这样的前终结符 (preterminal) 形容词共享部分比特位，表明模型已经学习到了词性。

处理复杂性

该模型可以很好地扩展到更长、更复杂的句子。下面是一个更深的树推导。请注意层次结构是如何从根节点一直保留到单个标记的。

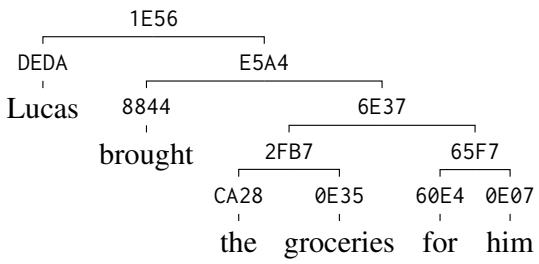
图 4: 展示深层层次树结构的推导示例。

结论

“Parserker2” 论文展示了无监督句法诱导方面的重大飞跃。通过从 零阶 升级到 一阶 CKY，研究人员使模型能够考虑跨度的内部结构，而不仅仅是边界。通过采用 对比哈希 和精心平衡的 损失函数 , 他们成功地仅利用原始文本训练出了这种复杂的结构。

这项工作意味着高质量的句法标注——通常是 NLP 中的瓶颈——现在可以以极低的成本获得。模型生成的二进制代码不仅仅是随机数字；它们是 LLM 一直向我们隐藏的“语法”的一种压缩、离散的表示。

对于学生和研究人员来说，这是一个强有力的提醒: 有时理解神经网络的最佳方法不是增加更多的层，而是施加正确的结构约束 (如 CKY) 并提出正确的问题 (如“这两个跨度是相同的吗？”) 。