引言

在当前的人工智能领域，像 GPT-4、PaLM 和 LLaMA 这样的大型语言模型 (LLM) 已成为自然语言处理的基石。它们拥有惊人的能力，但也伴随着巨大的代价: 推理效率。运行这些通常包含数十亿参数的庞大模型极其消耗资源。对于提供“语言模型即服务 (Language Model as a Service) ”的公司来说，处理来自数千用户的并发查询会造成巨大的瓶颈。

想象一下，有一辆公交车 (GPU) ，它被设计成一次只能搭载一名乘客 (用户查询) 。要运送 30 个人，这辆公交车必须跑 30 趟。这本质上就是标准串行推理的工作方式。它既缓慢又昂贵。

为了解决这个问题，研究人员一直在探索 数据多路复用 (Data Multiplexing) 。 这相当于想办法在那一趟公交车行程中安排多名乘客就座。通过将多个输入合并为一个复合输入，我们只需为多个用户运行一次繁重的 LLM 计算“前向传播”。

然而，这里有个陷阱。当你把不同的查询混合在一起时，模型往往会感到困惑。它很难区分哪个输出属于哪个输入，从而导致“幻觉”或答案混淆。以前的解决方案需要重新训练整个 LLM 来理解这种混合过程——对于如今庞大的预训练模型来说，这几乎是不可能完成的任务。

RevMUX 应运而生。在最近的一篇论文中，研究人员介绍了一种参数高效的框架，允许我们在不需要重新训练庞大骨干模型的情况下，混合输入 (多路复用) 并分离输出 (解复用) 。其核心秘诀是什么? 可逆适配器 (Reversible Adapters) 。

在这篇文章中，我们将拆解 RevMUX 的架构，解释其可逆设计背后的数学原理，并探讨它是如何在保持高准确率的同时加速推理的。

背景: 推理瓶颈

在深入了解 RevMUX 之前，我们需要了解高效推理的现状。业界通常通过两种方式来解决 LLM 速度慢的问题:

1. 以模型为中心的方法 (Model-Centric Approaches) : 这些方法试图使模型本身变小或变简单。像 量化 (Quantization) (将高精度的 32 位权重转换为 8 位或 4 位) 和 剪枝 (Pruning) (移除冗余连接) 就属于这一类。虽然有效，但它们物理上改变了模型。
2. 以算法为中心的方法 (Algorithm-Centric Approaches) : 这些方法优化计算的执行方式，例如 投机解码 (Speculative Decoding) 或优化键值 (KV) 缓存。

然而，这些方法都没有解决 批量吞吐量 (batch throughput) 的具体问题，即在不线性增加计算负载的情况下处理更多请求。通常情况下，如果你有 10 个输入，你就得做 10 倍的工作。

多输入多输出 (MIMO)

多输入多输出 (MIMO) 学习的概念提出了一种激进的转变: 在一次传递中处理多个输入。

在标准的 MIMO 设置中 (特别是 DataMUX )，一个“多路复用器 (Multiplexer) ”层将输入 \(x_1\) 和 \(x_2\) 组合成单个向量。神经网络处理这个向量。然后，一个“解复用器 (Demultiplexer) ”层尝试将结果拆分为 \(y_1\) 和 \(y_2\)。

以前尝试这种方法 (如 MUX-PLMs) 的问题在于，它们需要 端到端训练 。 你必须更新 BERT 或 GPT 模型的权重，以便它“学会”如何处理这些混合信号。对于一个 80 亿或 700 亿参数的模型来说，仅为了推理速度而微调整个模型不仅成本高昂，而且会造成存储噩梦 (你需要为每种不同的压缩率保存一份模型副本) 。

这就是 RevMUX 改变游戏规则的地方。它提出的问题是: 我们能否创建一个智能适配器，极其完美地混合和解开数据，以至于 LLM 甚至不知道它正在同时处理多个输入？

核心方法: RevMUX

RevMUX (Reversible Multiplexing，可逆多路复用) 旨在与 固定的、冻结的骨干 LLM 配合使用。它用三明治式的适配器包裹模型: 开头是多路复用层，结尾是解复用层。

让我们从高层次对比一下传统处理方式、DataMUX 和新的 RevMUX 架构。

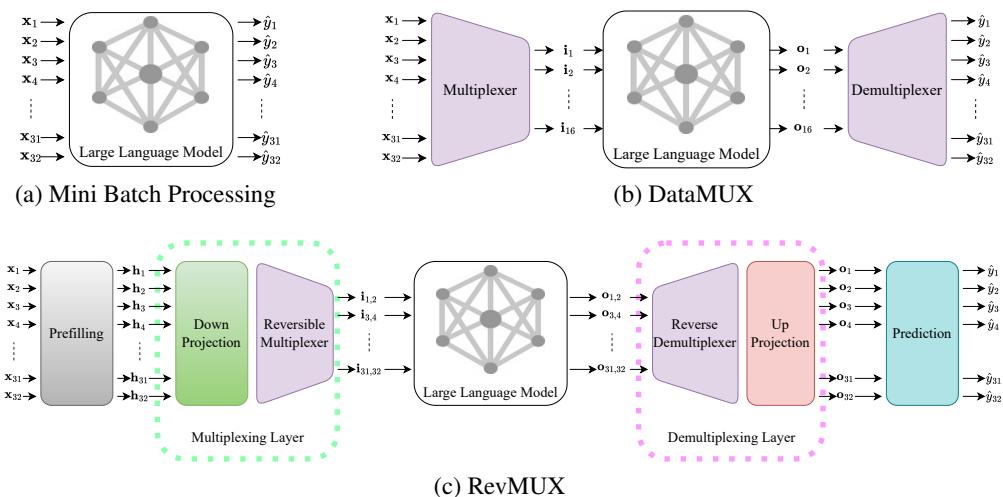
如 图 1 所示:

• (a) 小批量 (Mini Batch) : 每个输入 (\(x_1\) 到 \(x_{32}\)) 都有自己的独立通道。准确，但缓慢。
• (b) DataMUX: 将输入挤压在一起，但依赖于模型经过训练来处理这种挤压。
• (c) RevMUX: 使用特定的“可逆多路复用”层。它接收输入，将其投影降维，可逆地混合它们，通过冻结的 LLM，然后解开混合。

让我们分解 RevMUX 流程的三个不同阶段。

1. 预填充 (Prefilling) : 对齐特征空间

当你在数学上将两个句子混合在一起时，生成的向量通常看起来一点也不像一个真实的句子。这被称为 分布偏移 (distribution shift) 。 如果你将这个“怪异”的向量输入到冻结的 LLM 中，模型将不知道该如何处理它，因为它在预训练期间从未见过这样的数据。

为了解决这个问题，RevMUX 使用了 预填充 步骤。在混合之前，输入先经过 LLM 的前几层 (或提示编码器) ，将原始文本转换为模型“喜欢”的密集表示。

\[ \mathbf { h } _ { k } ^ { l } = \operatorname { E n c o d e r } _ { 0 : l } ( \mathbf { X } _ { k } ) , \]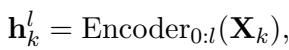

在这里，输入通过编码器的前 \(l\) 层。这确保了在我们开始混合特征之前，它们处于正确的语义空间中。

2. 多路复用层 (The Multiplexing Layer)

这是创新的核心。目标是将 \(N\) 个输入组合成一个。为了解释方便，我们假设我们要混合 2 个输入 (\(N=2\)) 。

首先，高维向量被投影降维以节省空间:

\[ \mathbf { i } _ { k } ^ { l } = f _ { \mathrm { d o w n } } ( \mathbf { h } _ { k } ^ { l } ) . \]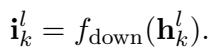

接下来是 可逆多路复用器 。 受可逆神经网络 (RevNets) 的启发，该模块以一种数学上保证可分离的方式分割和混合输入。

与简单的加法不同 (\(A + B = C\)，如果你只知道 C，你无法找回 A) ，RevMUX 使用了一组耦合函数。

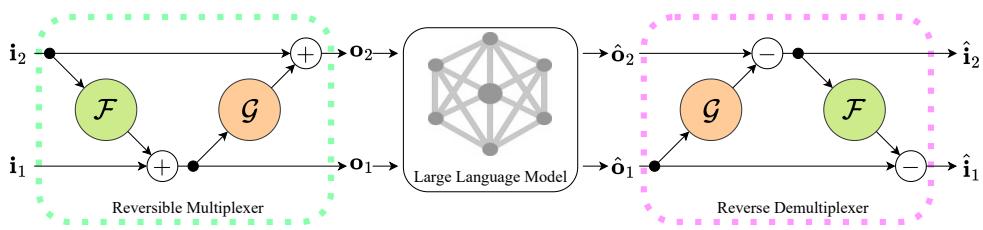
如 图 2 (左侧) 所示，混合过程通过两个阶段进行，使用可学习的函数 \(\mathcal{F}\) 和 \(\mathcal{G}\) (它们是小型的多层感知机 MLP) 。

混合的公式如下:

\[ \begin{array} { r l } & { \mathbf { o } _ { 1 } ^ { l } = \mathbf { i } _ { 1 } ^ { l } + \mathcal { F } ( \mathbf { i } _ { 2 } ^ { l } ) , } \\ & { \mathbf { o } _ { 2 } ^ { l } = \mathbf { i } _ { 2 } ^ { l } + \mathcal { G } ( \mathbf { o } _ { 1 } ^ { l } ) , } \\ & { \mathbf { o } ^ { l } = \mathrm { c o n c a t } [ \mathbf { o } _ { 1 } ^ { l } , \mathbf { o } _ { 2 } ^ { l } ] , } \end{array} \]

注意这里的依赖链:

1. 输出 1 (\(o_1\)) 是输入 1 加上输入 2 的某种变换。
2. 输出 2 (\(o_2\)) 是输入 2 加上已经计算出的输出 1 的某种变换。

这个组合后的输出 \(o^l\) 随后被送入庞大的、冻结的 LLM 中。

\[ \hat { \mathbf { o } } = \mathrm { D e c o d e r } \Big ( \mathrm { E n c o d e r } _ { l + 1 : L } \big ( \mathbf { o } ^ { l } \big ) \Big ) , \]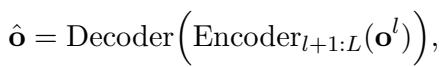

LLM 在这里完成它的繁重工作。由于输入被合并了，LLM 只需要运行一次，从而节省了大量的计算资源 (FLOPs) 。

3. 解复用层 (The Demultiplexing Layer)

在 LLM 产生输出后，我们得到了一个混合的结果向量。我们需要解开它，以获得用户 1 和用户 2 的具体预测结果。

由于多路复用器的设计是可逆的，解复用器仅仅是其数学逆运算。我们不需要“猜测”如何分离它们；我们直接计算出来。

观察 图 2 (右侧) 和下面的公式，我们以完全相反的顺序反转操作:

\[ \begin{array} { r } { \left[ \hat { \bf 0 } _ { 1 } , \hat { \bf 0 } _ { 2 } \right] = \hat { \bf 0 } , \qquad } \\ { \hat { \bf i } _ { 2 } = \hat { \bf 0 } _ { 2 } - \mathcal { G } ( \hat { \bf 0 } _ { 1 } ) , \qquad } \\ { \hat { \bf i } _ { 1 } = \hat { \bf 0 } _ { 1 } - \mathcal { F } ( \hat { \bf i } _ { 2 } ) , \qquad } \end{array} \]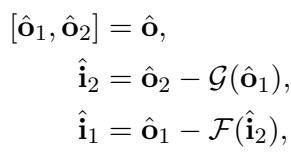

1. 首先，我们通过减去输出 1 的变换来恢复输入 2。
2. 然后，在恢复了输入 2 之后，利用它来恢复输入 1。

最后，我们将向量向上投影回原始维度 (\(f_{up}\)) ，并使用预测头生成分类标签。

\[ \begin{array} { r } { \hat { \bf h } _ { k } = f _ { \mathrm { u p } } ( \hat { \bf i } _ { k } ) , } \end{array} \]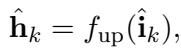

训练 RevMUX: 损失函数

该系统的美妙之处在于，我们只训练那些小型的适配器 (\(\mathcal{F}\), \(\mathcal{G}\), \(f_{down}\), \(f_{up}\)) 。LLM 中数十亿的参数保持不动。

为了训练这些适配器，作者结合使用了两个损失函数:

1. 交叉熵损失 (\(\mathcal{L}_{ce}\)) : 这是标准的“我们得到正确答案了吗？”的损失。它将模型的预测与真实标签 (Gold Label) 进行比较。

2. InfoNCE 损失 (\(\mathcal{L}_{info}\)) : 这很关键。由于骨干 LLM 是冻结的，它期望的输入必须具有某种特征。如果解复用出来的输出看起来像垃圾，最终的分类头就会失败。 InfoNCE 是一种对比损失。它强制解复用器输出的表示 (\(\hat{h}_k\)) 尽可能与我们正常 (逐个) 运行输入时模型本应产生的表示相似。

   \[ \begin{array} { l } { { \displaystyle { \mathcal L } _ { \mathrm { i n f o } } = \sum _ { k = 1 } ^ { N } \mathrm { I n f o N C E } ( \hat { \bf h } _ { k } , { \bf h } _ { k } ) } , \ ~ } \\ { { \displaystyle = \sum _ { k = 1 } ^ { N } - \mathbb E [ \log \frac { \exp ( \hat { \bf h } _ { k } \cdot { \bf h } _ { k } ) } { \exp ( \hat { \bf h } _ { k } \cdot { \bf h } _ { k } ) + \sum _ { j \ne k } ^ { N } \exp ( \hat { \bf h } _ { k } \cdot { \bf h } _ { j } ) } ] } } \end{array} \]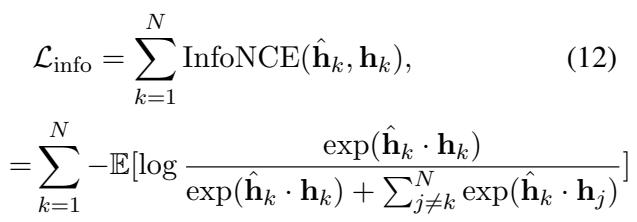

   

这个损失函数本质上是在告诉适配器: “确认为用户 1 恢复的向量看起来完全像用户 1 的原始向量，并且与用户 2 的向量截然不同。”

实验结果

理论听起来很扎实，但实际效果如何？研究人员在三种不同的 LLM 架构上测试了 RevMUX: BERT (仅编码器) 、T5 (编码器-解码器) 和 LLaMA-3 (仅解码器) ，使用了 GLUE 基准数据集 (如用于情感分析的 SST-2) 。

1. 与基线的性能对比

第一个主要测试是在 BERT-Base 上进行的。他们将 RevMUX 与以下方法进行了比较:

• DataMUX: 之前最先进的方法，需要训练整个模型。
• MUX-PLM: 另一种全训练方法。
• Vanilla Adapters (普通适配器) : RevMUX 的简化版，没有使用“可逆”数学原理。

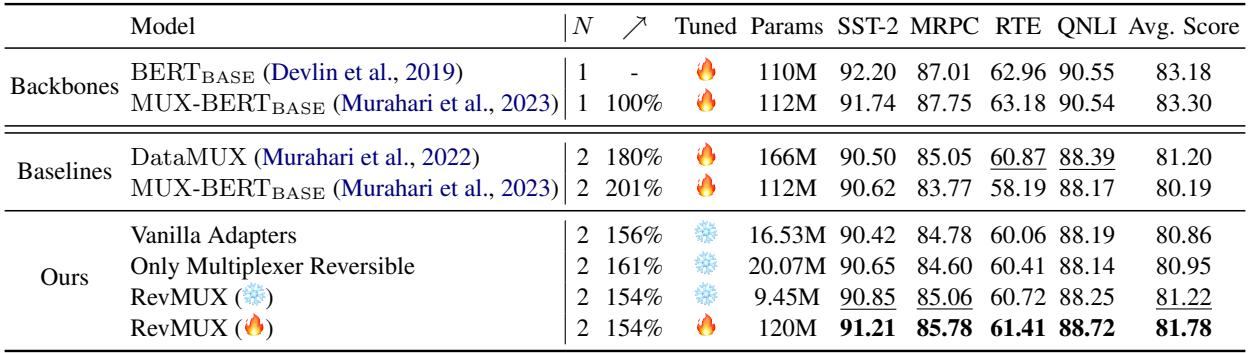
表 1 揭示了几个关键发现:

• RevMUX (❄️ 冻结) 取得了与完全微调的基线相当的性能。这非常了不起，因为与 DataMUX 相比，RevMUX 仅更新了一小部分参数。
• 可逆性至关重要: RevMUX 始终优于“普通适配器”。这证明了专门的可逆架构在混合过程中保持信号完整性方面发挥了重要作用。
• 加速: 在 \(N=2\) (混合 2 个输入) 的情况下，与逐个处理输入相比，模型实现了大约 1.5 倍到 1.6 倍的推理加速 。

2. 效率与准确性的权衡

速度总是有代价的。在数据多路复用中，代价通常是准确率的下降。

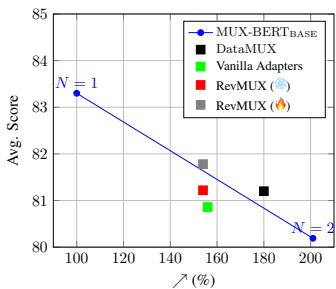
图 3 展示了这种权衡。

• X 轴代表效率 (吞吐量) ，Y 轴是准确率。
• 蓝线代表理想的基准线。
• 红圆圈 (RevMUX) 在相同的效率下比 黑方块 (DataMUX) 位于更高的位置。

这直观地表明，为了获得每一单位的速度提升，RevMUX 牺牲的准确率比竞争对手更少。它有效地“弯曲”了权衡曲线。

3. 扩展到更大的模型 (T5)

这是否只适用于像 BERT 这样的小模型？作者在三种不同规模 (Small, Base, Large) 的 T5 上进行了测试。

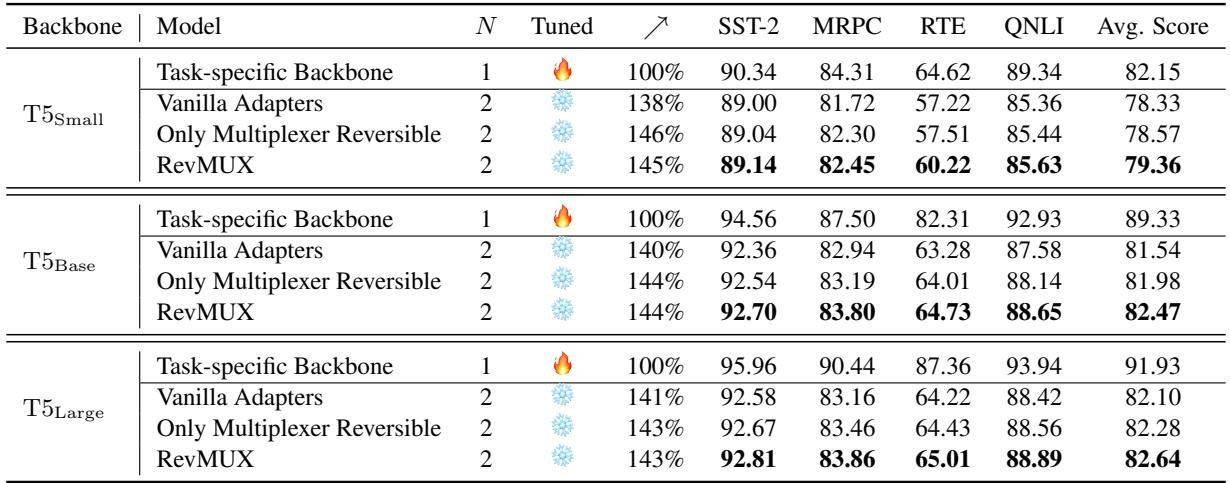
表 2 显示 RevMUX 具有良好的扩展性。在 T5-Large 上，使用 \(N=2\) 运行时提供了 143% 的加速 , 同时平均得分非常接近基线。

• T5-Large 基线 (N=1): 91.93 平均分
• RevMUX (N=2): 82.64 平均分

虽然性能有所下降 (这在将 2 个输入压缩为 1 个时是可以预期的) ，但速度增益是巨大的。值得注意的是，较大的模型 (\(T5_{Large}\)) 比较小的模型表现出略多的退化，突显了将其扩展到超大规模时面临的挑战。

4. 批量大小 (\(N\)) 的影响是什么？

我们可以把多少个输入挤在一起？2 个？4 个？16 个？

图 4 绘制了准确率与混合样本数 (\(N\)) 的关系。

• 随着 \(N\) 的增加 (X 轴向右移动) ，准确率自然下降。模型必须在一个向量中“记住”太多不同的输入。
• 预填充 (\(l\)) 的作用: 不同颜色的线代表不同层数的“预填充”。注意 \(l=6\) (绿线) 通常比 \(l=0\) (蓝色虚线) 在较大的 \(N\) 下保持更高的准确率。这证实了在混合之前对特征进行预处理对于高负载多路复用至关重要。

5. InfoNCE 损失有帮助吗？

最后，进行了一项消融实验，以观察那个复杂的对比损失函数 (\(\mathcal{L}_{info}\)) 是否真的是必要的。

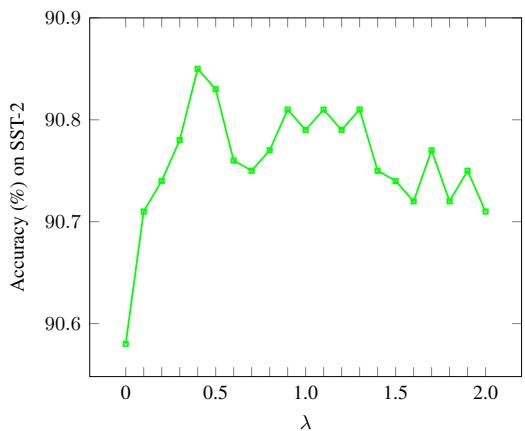
图 6 显示了随着 InfoNCE 损失权重 (\(\lambda\)) 的变化，SST-2 上的准确率变化。

• 当 \(\lambda = 0\) (没有 InfoNCE) 时，准确率较低 (~90.6%) 。
• 当 \(\lambda\) 增加到 0.5 - 1.0 左右时，准确率达到峰值 (~90.9%) 。
• 这证实了强制解复用的向量与原始向量相似，有助于冻结的骨干模型做出更好的预测。

结论与启示

RevMUX 代表了“绿色 AI”和高效计算向前迈出的重要一步。通过利用可逆神经网络的数学特性，作者创造了一种“欺骗”系统的方法——以一个输入的代价处理多个输入，而无需重新训练昂贵的骨干模型。

主要收获:

1. 即插即用: RevMUX 适用于冻结模型，这使得它适用于如今对大多数用户来说无法重新训练的大规模 LLM。
2. 可逆性是关键: 可逆适配器的设计比以前方法中使用的标准线性层能实现更好的信号重建。
3. 灵活的效率: 用户可以选择他们的权衡方案。如果他们需要 100% 的准确率，就使用标准推理。如果他们需要 2 倍的速度并且可以容忍 2-5% 的准确率下降，他们可以开启 \(N=2\) 的 RevMUX。

随着 LLM 规模的不断增长，像 RevMUX 这样优化等式“服务端”的技术将变得与模型本身一样重要。它为边缘设备上的实时应用打开了大门，并降低了大规模 AI 服务的碳足迹。

---