大语言模型 (LLM) 的发布目前面临着一个巨大的两难境地。一方面是“围墙花园”模式 (如 OpenAI 的 GPT-4 或 Anthropic 的 Claude) ，模型隐藏在 API 之后。这种方式保护了开发者的知识产权，但迫使用户将隐私数据发送到第三方服务器，引发了巨大的隐私担忧。

另一方面是开源模式 (如 Llama 或 Mistral) ，权重被公开分发。这对用户隐私非常有利——你可以在本地运行模型——但这对于那些失去模型所有权和控制权的开发者来说却是一场噩梦。一旦权重泄露，不良行为者可能会将其用于不道德的目的，或者竞争对手可能会在未经许可的情况下将其用于商业获利。

有没有中间地带？我们能否发布一个可以在本地运行的模型 (保护用户隐私) ，但同时保持实际权重通过某种方式保密 (保护开发者的所有权) ？

来自莱斯大学的研究人员及其合作者提出了一种名为 TaylorMLP 的迷人解决方案。利用泰勒级数 (Taylor Series) 展开的数学力量，他们找到了一种将模型权重“加密”为新格式的方法。这允许用户在本地运行模型，但——关键在于——会使生成过程变慢，从而防止大规模的商业滥用。他们戏谑地将这种减速机制称为“Taylor Unswift” (泰勒·不迅速) 。

在这篇文章中，我们将详细剖析 TaylorMLP 的工作原理、权重转换背后的数学原理，以及为什么这可能是未来安全模型分发的方向。

访问权限的两难境地

要理解为什么需要 TaylorMLP，我们首先需要直观地了解当前的 LLM 分发格局。

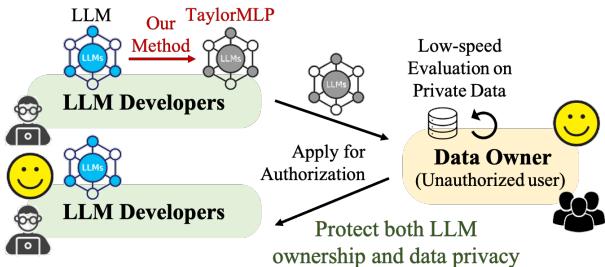
现有的 LLM 发布机制: (a) API 发布和 (b) 开源。我们提出 (c) TaylorMLP 以保护已发布 LLM 的所有权。

如 图 1 所示:

  1. API 发布 (a): 开发者保证了模型的安全，但用户必须上传私人数据。
  2. 开源 (b): 用户保证了数据的安全，但开发者失去了模型的所有权。
  3. TaylorMLP (c): 目标是允许用户在私人数据上评估模型，而开发者无需交出原始模型权重。

其核心思想是将模型转换为一种在输出上数学等效，但在结构上有所不同从而隐藏原始参数的格式。

背景: MLP 层

要保护 LLM，我们需要看看它的构建模块。Transformer 模型 (几乎所有现代 LLM 背后的架构) 由注意力 (Attention) 层和多层感知机 (MLP) 层组成。

一个标准的 MLP 层通常遵循以下流程:

  1. 线性投影: 输入 \(x\) 乘以权重。
  2. 激活: 应用非线性函数 (如 GELU 或 SiLU) 。
  3. 线性投影: 结果再乘以另一组权重。

在数学上，MLP 层中特定维度的输出 \(y_i\) 如下所示:

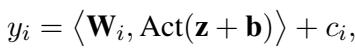
描述标准 MLP 输出的方程。

在这里，\(\mathbf{W}\) 和 \(\mathbf{b}\) 是我们想要保护的权重和偏置。如果你把这些给了用户，你就泄露了模型。TaylorMLP 提出了一种方法，用一组源自微积分的不同参数来替换这些特定的矩阵。

核心方法: 泰勒展开

如果你还记得本科微积分的话, 泰勒级数允许你将一个复杂函数近似为无穷项之和，这些项是根据该函数在某一点的导数值计算得出的。

研究人员意识到，LLM 中的激活函数 (如 GELU) 可以使用泰勒级数进行展开。通过这样做，他们可以将权重矩阵混合到多项式系数中。

1. 架构转变

让我们比较一下标准架构和 TaylorMLP 架构。

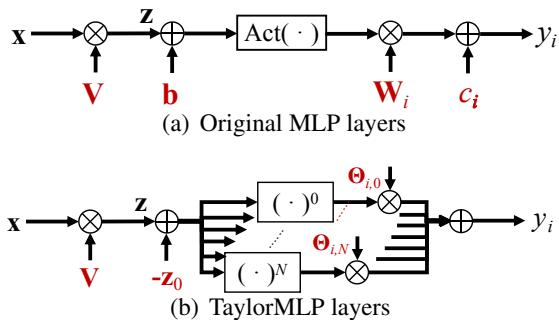
比较 (a) 原始 MLP 层和 (b) TaylorMLP 层。

在 图 2(a) 中，你看到的是标准路径: \(x \to z \to \text{Act}(z+b) \to y\)。 在 图 2(b) 中，显式权重 \(\mathbf{b}\)、\(\mathbf{W}\) 和 \(\mathbf{c}\) 消失了。取而代之的是一系列代表泰勒展开不同阶数 (\(N=0\) 到 \(N\)) 的并行分支。

2. 魔法背后的数学

我们如何摆脱这些权重？我们首先围绕一个“局部嵌入”点 \(\mathbf{z}_0\) 展开激活项 \(\text{Act}(\mathbf{z} + \mathbf{b})\)。

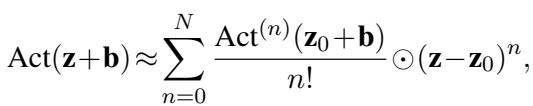
激活函数的泰勒展开。

这个方程看起来很复杂，但它只是一个标准的泰勒展开式。有趣的部分发生在我们把这个展开式代回原始的 MLP 方程时。通过重新排列各项，研究人员将原始权重 \(\mathbf{W}\) 与激活函数的导数合并在了一起。

这引出了隐参数 (Latent Parameters) 的定义，表示为 \(\Theta\) (Theta) 。

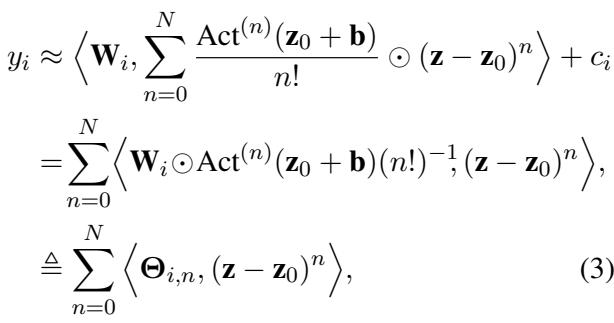
TaylorMLP 输出公式的推导。

这里至关重要的创新是上面的公式 (3)。现在的输出 \(y_i\) 是使用 \(\Theta_{i,n}\) 和输入数据计算出来的。原始权重 \(\mathbf{W}\) 和偏置 \(\mathbf{b}\) 被“融合进”了这些 \(\Theta\) 参数中。

这些新的安全参数的定义如下:

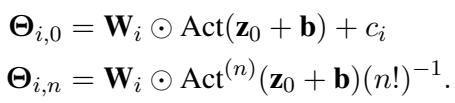
Theta 参数的定义。

为什么这是安全的? 你 (用户) 得到的是 \(\Theta\)。要还原原始的 \(\mathbf{W}\) 和 \(\mathbf{b}\)，你需要对泰勒级数组合进行逆向工程。论文证明了这个过程实际上是不可逆的，因为多种权重组合可能产生相似的 \(\Theta\) 值，而且在没有原始种子的情况下，重建是不可行的。

3. “Unswift” 机制 (减慢生成速度)

你可能会问: “如果输出是一样的，为什么这能防止滥用？”

答案在于计算复杂度 。 在标准 MLP 中，你只需要进行一次传递。而在 TaylorMLP 中，为了获得准确的结果，你必须对级数的多个项 (从 \(n=0\) 到 \(N\)) 进行求和。

  • 如果 \(N=0\)，模型速度快但不准确 (会出现幻觉) 。
  • 如果 \(N=8\)，模型是准确的，但需要更多的浮点运算 (FLOPs) 。

研究人员将这种故意造成的延迟称为 “Taylor Unswift” 。 它使延迟增加了大约 \(4\times\) 到 \(10\times\)。

这是一个特性，而不是漏洞。它允许个人研究人员或开发者在他们的私人数据上测试模型 (速度在这里并不关键) ，但对于竞争对手来说，拿走这个模型并通过商业 API 为数百万用户提供服务在经济上变得不可行。

4. 收敛性

这种近似真的有效吗？理论上是的。随着项数 (\(N\)) 趋向于无穷大，TaylorMLP 的输出将与原始 MLP 的输出完全一致。

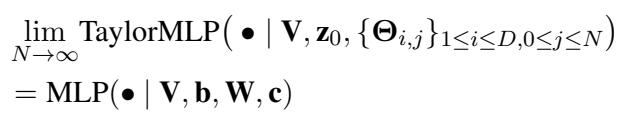
当 N 趋向于无穷大时 TaylorMLP 的极限。

然而，我们无法计算无穷多项。我们需要找到 \(N\) 的一个“最佳平衡点”，在这个点上模型既足够准确以供使用，又足够慢以提供保护。

5. 激活函数的导数

为了实现这一点，我们需要像 GELU 和 SiLU 这样函数的高阶导数。这很快就会变得复杂。下面的可视化图展示了随着阶数 (\(n\)) 的增加，GELU 的导数是如何变化的。

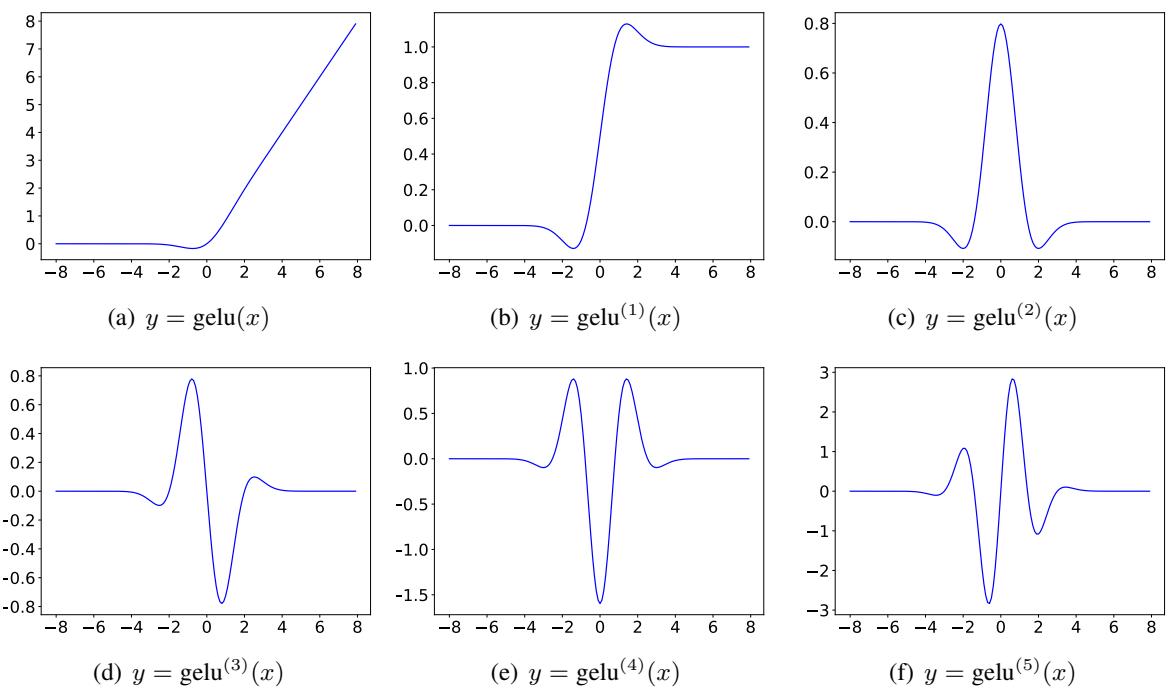
GELU 导数的可视化。

随着 \(n\) 的增加 (从 a 到 f) ，函数变得越来越具有震荡性。TaylorMLP 方法依赖于准确计算这些形状来重建激活行为。

实验结果

研究人员在三个主要模型系列上测试了 TaylorMLP: Llama-3-8B、Mistral-7B 和 Phi-2 。 他们评估了准确性保留情况和延迟增加情况。

RQ1: 准确性 vs. 延迟

最关键的问题是: 模型还能用吗？

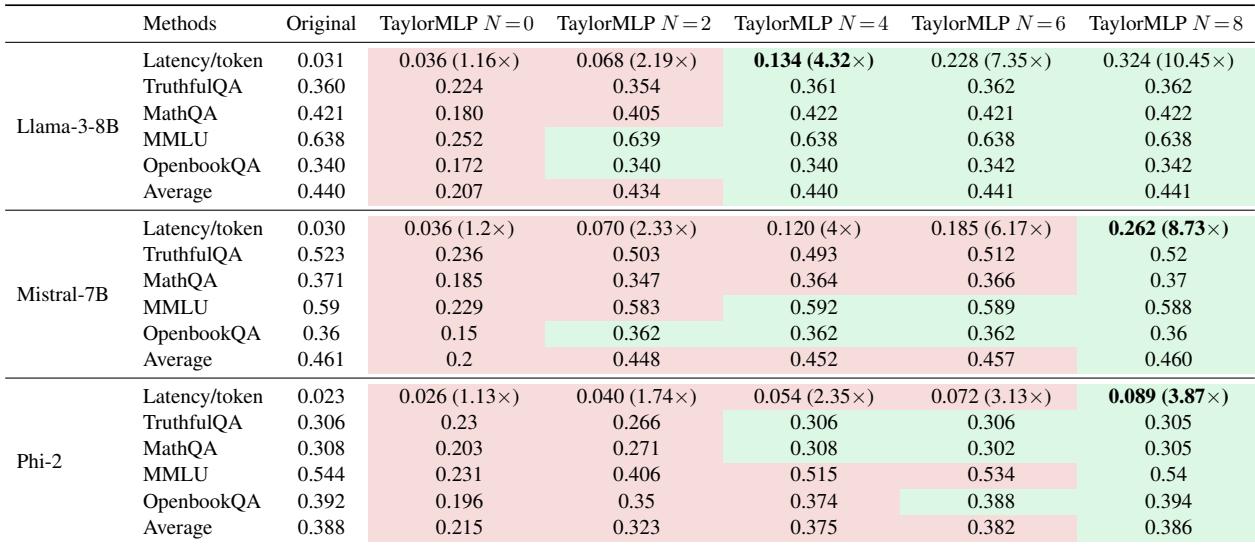
表 1: TaylorMLP 与原始 LLM 的准确性和每 token 延迟对比。

从表 1 得出的关键结论:

  1. 精度恢复: 查看 \(N=0\) 与 \(N=8\) 的列。在 \(N=0\) 时，准确率 (例如在 MMLU 上) 显著下降。然而，在 \(N=8\) 时，准确率与“Original” (原始) 列几乎相同。
  2. 延迟增加: 现在看看“Latency/token” (每 token 延迟) 行。对于 Llama-3-8B，原始延迟是 0.031秒。在 \(N=8\) 时，它跃升至 0.324秒——增加了 10.45倍 。

这证实了“Unswift”假设: 模型变得准确但显著变慢。

RQ2: 权重会被窃取吗？

研究人员模拟了攻击场景，其中“未经授权的用户”试图通过微调和蒸馏来重建模型。

微调攻击: 攻击者试图重新初始化权重，并在下游数据集 (TruthfulQA、MathQA 等) 上微调模型，看看能否恢复性能。

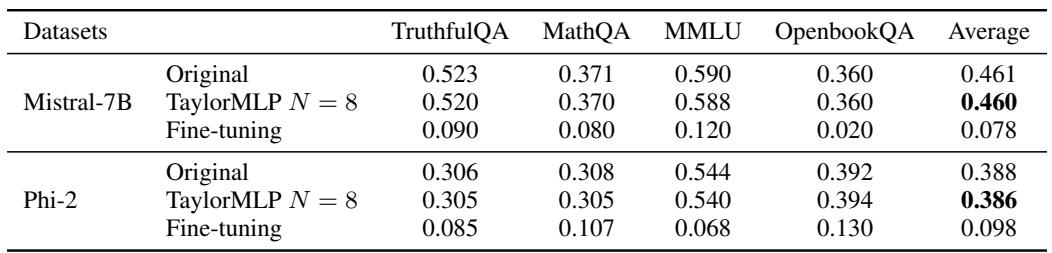
表 2: 微调后的 LLM 与 TaylorMLP 模型的准确性对比。

如 表 2 所示，微调后的模型 (模拟被盗权重) 表现糟糕 (例如 MMLU 上为 0.120，而 TaylorMLP 为 0.588) 。这证明仅仅拥有架构和数据集是不够的；你需要特定的受保护权重。

蒸馏攻击: 攻击者试图将 TaylorMLP 模型中的知识“蒸馏”到一个标准的、快速的模型中。

表 3: 困惑度结果。

表 3 显示，蒸馏后的模型困惑度为 256.62 (越低越好) ，而 TaylorMLP 为 12.75 。 蒸馏出的模型本质上是垃圾，会产生幻觉。

RQ3: 我们需要多少项 (\(N\)) ？

展开阶数 \(N\) 与性能之间的关系在 图 5 中清晰可见。

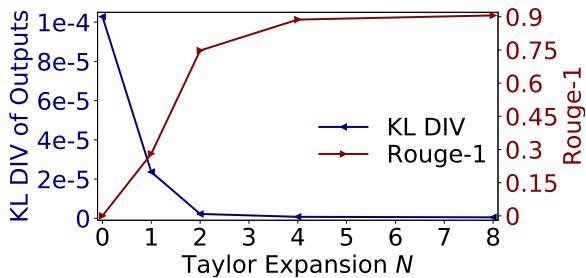
KL 散度和 ROUGE 分数与展开阶数的关系。

  • 蓝线 (KL 散度): 这衡量输出概率与原始模型的差异。它在 \(N=4\) 到 \(N=8\) 左右降至接近零。
  • 红线 (ROUGE-1): 这衡量文本重叠度。随着 \(N\) 的增加，它回升至接近 1.0 (完美匹配) 。

这表明 \(N=8\) 是保持质量的神奇数字。

结论与启示

TaylorMLP 代表了解决“开放权重”与“API”之争的一种新颖方法。它创造了一个新的模型发布类别: 安全权重 (Secured Weights) 。

为什么这很重要?

  1. 先试后买: 用户可以下载专有模型的 TaylorMLP 版本。他们可以在敏感的医疗或金融数据上运行它，看看效果如何，而无需向开发者泄露数据。
  2. 知识产权保护: 开发者可以发布这些“演示”版本，而不必担心竞争对手会利用他们的辛勤工作建立高速 API 服务，这要归功于延迟惩罚。
  3. 监管合规: 这允许在受限环境中对模型进行安全审计。

通过将权重转换为泰勒级数参数，TaylorMLP 确保了模型的“秘方”保持隐藏，同时其功能效用——尽管是“慢动作”的——仍然对世界开放。这是基础微积分在解决现代 AI 难题上的一次巧妙应用。