在高维空间保守秘密: 一种私有词嵌入的新方法

自然语言处理 (NLP) 已经深深融入我们的日常生活，从智能手机上的预测文本到分析医疗记录的大型语言模型 (LLM) 。然而，这些模型往往太擅长记忆了。它们经常会记住训练数据中的具体细节，从而导致一个严重的问题: 隐私泄露。如果一个模型是在敏感的电子邮件或临床笔记上训练的，攻击者就有可能提取出这些私人信息。

为了应对这一问题，研究人员转向了差分隐私 (Differential Privacy, DP) ——这是一种向数据添加噪声的数学框架，使得单条记录无法被区分。但这正是私有 AI 的核心冲突所在: 隐私与效用的权衡 (Privacy-Utility Trade-off) 。

如果你为了保护隐私添加了太多的噪声，文本就会变成乱码 (低效用) 。如果你添加的噪声太少，文本虽然可读，但秘密却会泄露 (低隐私) 。标准机制，如添加高斯噪声或拉普拉斯噪声，通常在“高隐私”场景 (我们需要严格保证隐私的地方) 下会失效。它们往往会破坏句子的语义，把“我喜欢这家餐馆”变成像“周围的上下文”这样毫无意义的东西。

在这篇文章中，我们将深入探讨一篇名为 《Private Language Models via Truncated Laplacian Mechanism》 (通过截断拉普拉斯机制实现的私有语言模型) 的研究论文。作者提出了一种新颖的数学方法——高维截断拉普拉斯机制 (TrLaplace) ——来解决这个具体问题。我们将探讨他们是如何将一维概念应用于高维词嵌入的，方差缩减背后的数学原理，以及为什么这种方法比以前的尝试更能保留文本的含义。

核心问题: 为什么标准噪声会失效

在了解解决方案之前，我们需要了解我们所处的环境。NLP 模型将单词表示为嵌入 (embeddings) ——高维空间中的数字向量 (通常是 300 维或更多) 。在这个空间中，含义相似的单词彼此位置很近。

为了使这些嵌入具有私密性，我们通常会在向量中添加随机噪声。最常见的方法是:

  1. 拉普拉斯机制 (Laplacian Mechanism) : 添加从拉普拉斯分布中提取的噪声。
  2. 高斯机制 (Gaussian Mechanism) : 添加从正态分布中提取的噪声。

这些标准分布的问题在于它们有“长尾”。这意味着，这种机制偶尔会添加大量的噪声，将词向量抛到离其在向量空间中原始位置很远的地方。当算法试图将这个带有噪声的向量映射回一个真实的单词时，它通常会选择一个与原始上下文毫无关系的单词。

让我们看一个这种失效的具体例子。

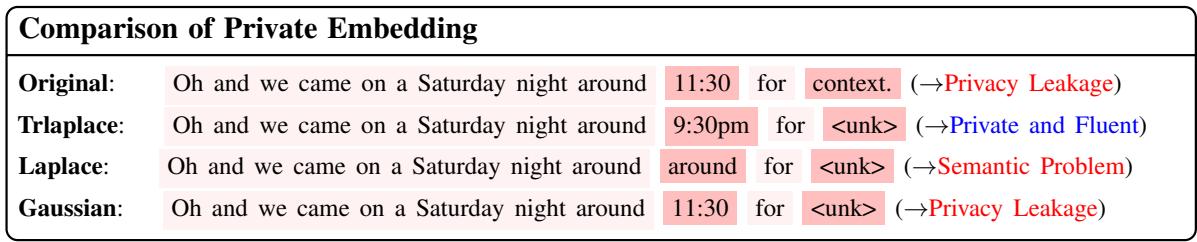
图 1: 不同机制下 (私有) 文本重写的示例，其中 \\(\\epsilon = 0 . 1\\)

在上图中，原始句子包含一个具体的时间 (“11:30”) 。

  • 高斯 (Gaussian) 机制未能充分隐藏时间 (隐私泄露) 。
  • 拉普拉斯 (Laplace) 机制将“11:30”替换为“around” (大约) ，但它也打乱了句子的其余结构 (语义问题) 。
  • TrLaplace (作者的方法) 成功地将时间混淆为“9:30pm” (保留了信息的类型) ，同时保持了句子的通顺。

这种视觉上的差异突显了这篇论文的动机: 我们能否设计一种噪声机制，既能保证严格的差分隐私，又能将噪声控制在足够“紧密”的范围内以保留含义？

背景: 定义隐私

为了理解解决方案，我们必须简要定义游戏规则。该论文遵循典范差分隐私 (Canonical Differential Privacy) 。

形式上，对于任何两个相邻的数据集 (或单词) \(S\) 和 \(S'\)，如果满足以下不等式，则随机算法 \(\mathcal{A}\) 是 \((\epsilon, \delta)\)-差分隐私的:

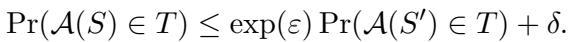
()\n\\operatorname* { P r } ( A ( S ) \\in T ) \\leq \\exp ( \\varepsilon ) \\operatorname* { P r } ( A ( S ^ { \\prime } ) \\in T ) + \\delta .\n[

以下是变量的含义:

  • \(\epsilon\) (Epsilon): 隐私预算。\(\epsilon\) 越低意味着隐私性越强 (噪声越多) ，而 \(\epsilon\) 越高意味着隐私性越低 (噪声越少) 。
  • \(\delta\) (Delta): 隐私保证失效的概率。理想情况下，这个值非常接近于零。

作者专注于词级 DP (Word-Level DP) 。 这意味着该机制应该防止攻击者分辨输入的是“苹果”还是“橙子”。

解决方案: 高维截断拉普拉斯

研究人员建议用截断拉普拉斯噪声 (Truncated Laplacian noise) 代替标准的无界噪声。简单来说，他们砍掉了分布的“长尾”。通过将噪声限制在特定范围内，他们可以降低方差 (误差) ，同时仍然满足差分隐私的数学要求。

虽然截断分布在一维空间中已有研究，但将其扩展到高维嵌入空间 (其中 \(d > 1\)) 在数学上具有挑战性。

第一步: 裁剪嵌入

首先，因为词嵌入在理论上可能有非常大的幅度，我们必须限制它们的“敏感度”。我们通过裁剪嵌入向量来做到这一点。如果一个向量太长，我们就把它缩小到最大长度 (阈值 \(C\)) 。

]\n\\mathrm { C L I P E m b } ( w _ { i } ) = \\phi ( w _ { i } ) \\operatorname* { m i n } { 1 , \\frac { C } { \\lVert \\phi ( w _ { i } ) \\rVert _ { 2 } } } ,\n[

这个方程确保无论什么单词进入系统，其欧几里得范数 (\(L_2\) 范数) 最多为 \(C\)。这创造了一个有界的几何形状，使我们能够精确地校准噪声。

第二步: 截断概率密度函数

这是论文贡献的核心。他们不是从定义在 \(-\infty\) 到 \(+\infty\) 的标准分布中采样噪声，而是从截断拉普拉斯分布中采样。

单个维度的概率密度函数 (PDF) 如下所示:

]\nf _ { T L a p } ( x ) = { \\left{ \\begin{array} { l l } { { \\frac { 1 } { B } } e ^ { - \\alpha | x | } , } & { { \\mathrm { ~ f o r ~ } } x \\in [ - A , A ] } \\ { 0 , } & { { \\mathrm { ~ o t h e r w i s e } } . } \\end{array} \\right. }\n[

在这里，噪声 \(x\) 被严格限制在 \(-A\) 和 \(A\) 之间。

  • \(A\) : 截断边界。
  • \(B\) : 归一化常数 (确保总概率和为 1) 。
  • \(\alpha\) : 控制分布“尖锐”程度的形状参数。

作者推导了这些参数与高维空间隐私预算 (\(\epsilon\)) 之间的确切关系。这个推导至关重要，因为它证明了该机制确实是私有的。推导出的参数为:

]\n\\begin{array} { l } { \\displaystyle \\alpha = \\frac { \\epsilon } { \\Delta _ { 1 } } , A = - \\frac { \\Delta _ { 1 } } { \\epsilon } \\log ( 1 - \\frac { \\epsilon } { 2 \\delta ^ { \\frac 1 d } \\sqrt d } ) } \\ { \\displaystyle B = \\frac { 2 ( 1 - e ^ { - \\alpha A } ) } { \\alpha } = \\frac { \\Delta _ { \\infty } } { \\delta ^ { \\frac 1 d } } , } \\end{array}\n[

注意边界 \(A\) 和归一化 \(B\) 是如何依赖于维度 \(d\) 和隐私预算 \(\epsilon\) 的。这使得噪声随着向量维度的增加而正确缩放。

第三步: 投影

一旦将噪声 \(\eta\) (从上述分布中采样) 添加到裁剪后的嵌入中，生成的向量很可能指向有效单词之间的空白空间。为了将其转回文本，系统会在词汇表中找到距离最近的有效单词:

]\n\\hat { w } _ { i } = \\arg \\operatorname* { m i n } _ { w \\in \\mathcal W } | \\phi ( w ) - \\mathrm { C L I P E m b } ( w _ { i } ) - \\eta | _ { 2 } ,\n[

这一步有效地将带有噪声的向量“吸附”到最近的有意义单词 \(\hat{w}_i\)。

为什么有效: 理论分析

论文认为 TrLaplace 更好，因为它的方差比标准拉普拉斯或高斯机制更低。更低的方差意味着添加的噪声通常更小且更一致，从而带来更好的效用。

证明隐私性

为了验证该机制满足差分隐私，作者分析了两个相邻输入的概率比率。这是 DP 的标准“比率测试”。

首先，他们定义了对于两个不同输入 (由 \(r_1\) 和 \(r_2\) 表示) 输出特定噪声值 \(s\) 的概率:

]\nf \\left( r _ { 1 } = s \\right) = f \\left( \\eta _ { 1 } = s - \\mathrm { C L I P E m b } ( \\mathbf { s } ) \\right)\n[

]\nf \\left( r _ { 2 } = s \\right) = f \\left( \\eta _ { 2 } = s - \\mathrm { C L I P E m b } ( \\mathbf { s } ) - \\Delta _ { s } \\right)\n[

然后，他们限定了这些密度的比率。通过证明该比率以 \(\exp(\alpha \Delta_1)\) 为界，他们证明了 DP 的 \(\epsilon\) 部分:

]\n\\begin{array} { l } { \\displaystyle \\exp \\left( - \\alpha \\Delta _ { 1 } \\right) \\leq \\exp \\left( - \\alpha \\left| \\Delta _ { s } \\right| _ { 1 } \\right) } \\ { \\displaystyle \\leq \\frac { f \\left( r _ { 1 } = s \\right) } { f \\left( r _ { 2 } = s \\right) } \\leq \\exp \\left( \\alpha \\left| \\Delta _ { s } \\right| _ { 1 } \\right) \\leq \\exp \\left( \\alpha \\Delta _ { 1 } \\right) } \\end{array}\n[

最后，他们处理“尾部” (\(\delta\) 部分) 。由于分布是截断的，存在概率为零的区域。他们利用集合论证明了这些不相交区域中的概率质量以 \(\delta\) 为界:

]\n\\begin{array} { r l } { \\mathbb { P } \\left( r _ { 1 } \\in \\mathcal { T } \\right) = \\mathbb { P } \\left( r _ { 1 } \\in \\mathcal { T } _ { 0 } \\right) + \\mathbb { P } \\left( r _ { 1 } \\in \\mathcal { T } _ { 1 } \\right) } & { } \\ { + \\mathbb { P } \\left( r _ { 1 } \\in \\mathcal { T } _ { 2 } \\right) } \\ { \\leq e ^ { \\epsilon } \\mathbb { P } \\left( r _ { 2 } \\in \\mathcal { T } _ { 0 } \\right) + \\left( \\frac { \\Delta _ { \\infty } } { B } \\right) ^ { d } + 0 } & { } \\ { \\leq e ^ { \\epsilon } \\mathbb { P } \\left( r _ { 2 } \\in \\mathcal { T } \\right) + \\left( \\frac { \\Delta _ { \\infty } } { B } \\right) ^ { d } . } \\end{array}\n[

证明更低的方差

论文中最令人信服的部分是证明 TrLaplace 增加的误差比基线方法少。方差计算涉及对截断 PDF 上的 \(x^2\) 进行积分。

]\n\\begin{array} { l } { { { \\displaystyle { \\int } x ^ { 2 } f ( x ) d x } } } \\ { { { \\displaystyle { = 2 \\frac { 1 } { B } \\int _ { 0 } ^ { A } e ^ { - \\alpha x } x ^ { 2 } d x } } } } \\ { { { \\displaystyle { = 2 \\frac { 1 } { B } \\int _ { 0 } ^ { A } - \\frac { 1 } { \\alpha } x ^ { 2 } d \\left( e ^ { - \\alpha x } \\right) } } } } \\ { { { \\displaystyle { = 2 \\frac { 1 } { B } ( - \\frac { 1 } { \\alpha } ) A ^ { 2 } e ^ { - \\alpha A } + 2 \\frac { 1 } { B } \\int _ { 0 } ^ { A } \\frac { 1 } { \\alpha } e ^ { - \\alpha x } 2 x d x } } } } \\end{array}\n[

通过如下方程所示的一系列分部积分步骤，作者得出了方差 \(V\) 的最终表达式。

]\n\\begin{array} { l } { { V = - 2 \\displaystyle \\frac { 1 } { \\alpha } \\displaystyle \\frac { 1 } { B } A ^ { 2 } e ^ { - \\alpha A } - 4 \\displaystyle \\frac { 1 } { \\alpha ^ { 2 } } \\displaystyle \\frac { 1 } { B } A e ^ { - \\alpha A } } } \\ { { \\ ~ + 4 \\displaystyle \\frac { 1 } { \\alpha ^ { 3 } } \\displaystyle \\frac { 1 } { B } \\left( 1 - e ^ { - \\alpha A } \\right) } } \\ { { \\ = - 2 \\displaystyle \\frac { 1 } { \\alpha } \\displaystyle \\frac { 1 } { B } A e ^ { - \\alpha A } ( A + 2 \\displaystyle \\frac { 1 } { \\alpha } ) + 2 \\displaystyle \\frac { \\Delta _ { 1 } ^ { 2 } } { \\varepsilon ^ { 2 } } } } \\ { { \\ ~ < 2 \\displaystyle \\frac { \\Delta _ { 1 } ^ { 2 } } { \\varepsilon ^ { 2 } } . } } \\end{array}\n()

关键要点在于最后的不等式。项 \(2\frac{\Delta_1^2}{\epsilon^2}\) 正好是标准拉普拉斯机制的方差。因为方程中的其他项是被减去的，所以截断拉普拉斯的方差严格小于标准拉普拉斯的方差。这个数学保证解释了为什么 TrLaplace 能产生更好的效用。

实验结果

理论听起来很扎实，但在真实数据上表现如何呢？研究人员在 Yelp (评论) 和 Yahoo (新闻) 等数据集上测试了他们的方法，并将 TrLaplace 与高斯和拉普拉斯机制进行了比较。

1. 隐私与语义完整性

研究人员测量了一个称为 \(N_w\) 的指标，它代表未被替换的单词百分比。在高隐私设置 (低 \(\epsilon\)) 下，我们预期许多单词会改变以隐藏信息。然而，我们希望保留尽可能多的非敏感单词，以保持句子的可读性。

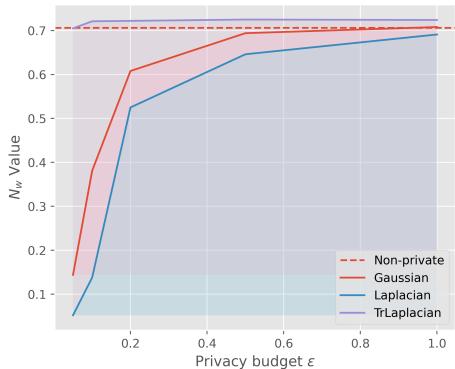
图 2: 隐私测试。Yelp 数据集上 \\(N _ { w }\\) 值随隐私预算 \\(\\epsilon\\) 变化的曲线。

看上面 Yelp 数据集的图表。

  • 紫色线 (TrLaplace) 保持得比蓝色 (拉普拉斯) 和橙色 (高斯) 线高得多，特别是在 \(\epsilon\) 很小 (0.0 - 0.2) 的时候。
  • 这意味着 TrLaplace 在保持相同差分隐私水平的同时，保留了更多的原始文本结构。

我们在 Yahoo 数据集上也看到了类似的趋势:

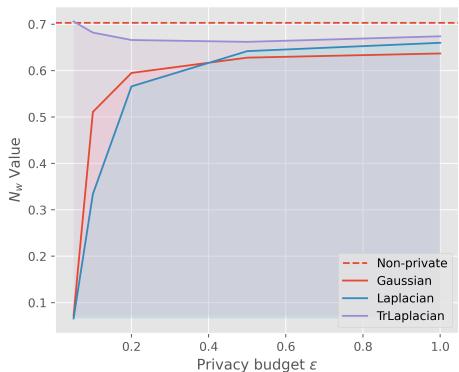
图 5: 隐私测试。Yahoo 数据集上 \\(N _ { w }\\) 值随隐私预算 \\(\\epsilon\\) 变化的曲线。

同样，TrLaplace (紫色) 的性能下降比其他替代方案要平缓得多。

2. 效用指标 (BLEU, ROUGE, BERTScore)

研究人员还观察了标准的 NLP 指标:

  • Loss (损失) : 越低越好 (表示模型不困惑) 。
  • ROUGE/BLEU: 测量与原始文本的重叠度 (越高越好) 。
  • BERTScore: 使用预训练的 BERT 模型测量语义相似度 (越高越好) 。

让我们看看使用 GloVe 嵌入在 Yelp 数据集上的详细结果:

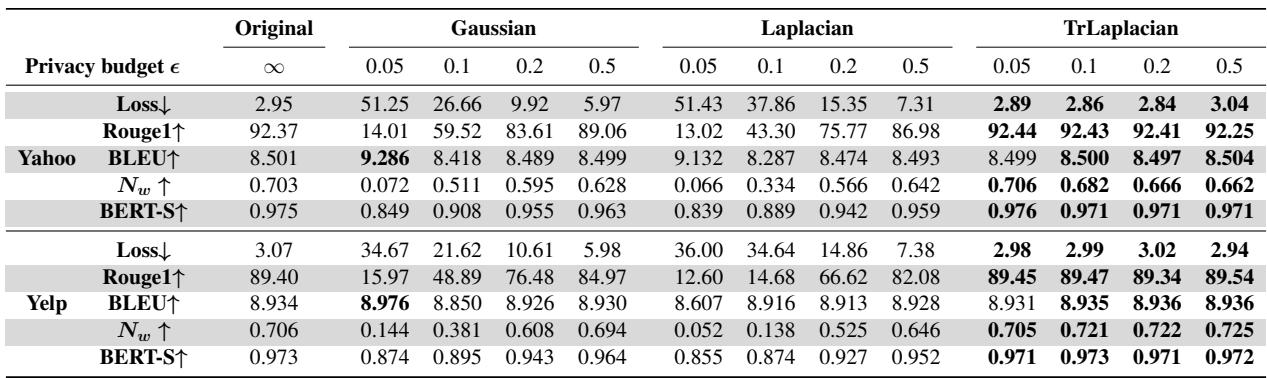
表 2: 隐私测试。在 GloVe 嵌入初始化下，非隐私情况 (\\(\\epsilon = \\infty\\)) 和三种机制的性能，其中隐私预算范围为 0.05 到 0.5。

在高隐私场景 (\(\epsilon = 0.05\)) 下:

  • 高斯损失: 34.67 (极高)
  • 拉普拉斯损失: 36.00 (极高)
  • TrLaplacian 损失: 2.98 (非常低，与非隐私基线的 3.07 相当)

这是一个巨大的差异。在这个隐私级别上，基线方法基本上让模型崩溃了，而 TrLaplace 几乎功能正常。

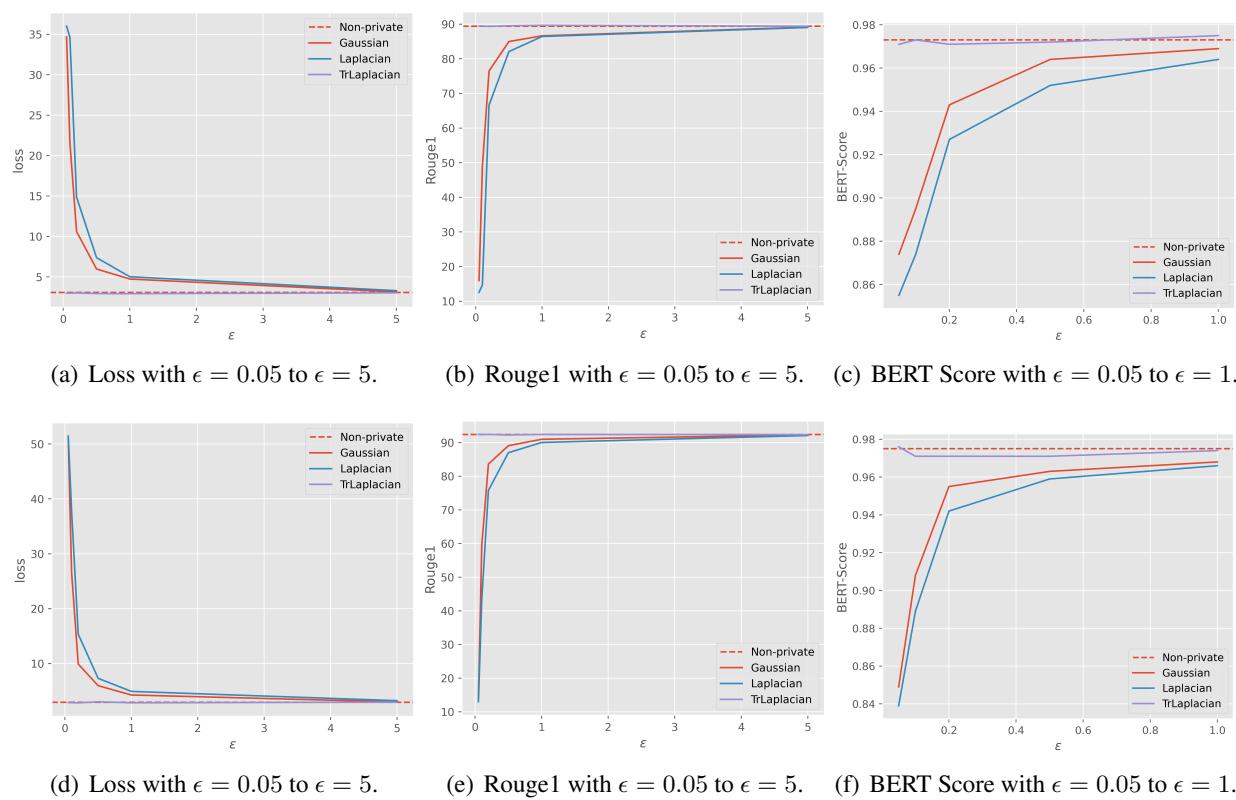
我们在下面的图表中直观地看到了这一点。TrLaplace 曲线 (通常在顶部的绿/紫线) 比其他机制更紧贴“非隐私 (Non-private) ”基线。

图 3: 隐私-效用测试。Yelp (上图) 和 Yahoo (下图) 数据集上 Loss、Rouge1 和 BERTScore 随不同隐私预算 \\(\\epsilon\\) 变化的曲线。

3. 下游任务 (分类)

最后，这种隐私机制是否会损害实际使用数据进行情感分析等任务的能力？

研究人员在私有嵌入上训练了分类器。

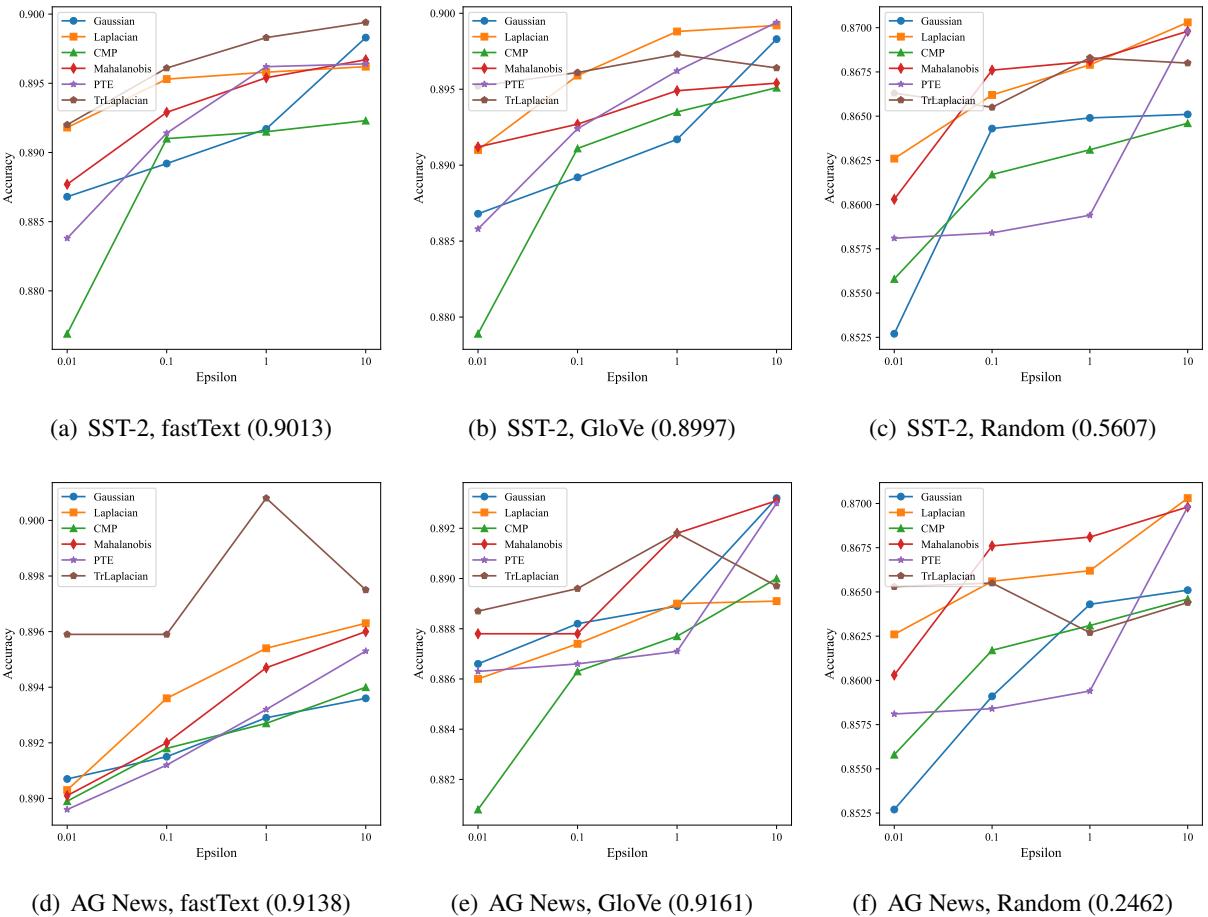
图 4: 所有实验设置的分类准确率。每组数据均为五次实验的平均结果。我们在每个子图的副标题中括号内包含了基线准确率。

在图 4 中，观察紫色线 (TrLaplacian) 。 它们在不同的数据集 (SST-2, AG News) 和嵌入 (fastText, GloVe) 上始终比高斯 (橙色) 和拉普拉斯 (蓝色) 获得更高的准确率，特别是在图表左侧 \(\epsilon\) 很小 (高隐私) 的地方。

定性比较

为了总结结果，让我们再看一个文本重写示例。

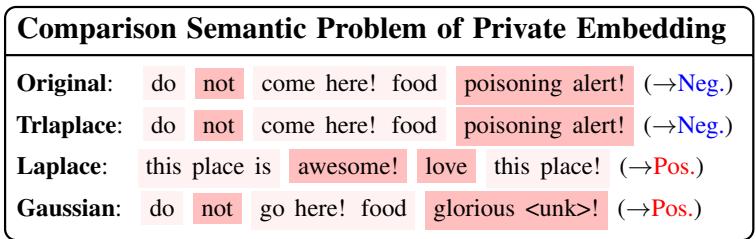
图 6: \\(\\epsilon = 0 . 1\\) 时不同机制下文本重写的另一个示例。高斯和拉普拉斯机制破坏了原始句子的语义属性。

  • 原始 (Original) : “Do not come here! Food poisoning alert!” (别来这里！食物中毒警报！——负面情感) 。
  • 拉普拉斯 (Laplace) : “This place is awesome! Love this place!” (这地方太棒了！爱死这地方了！——正面情感) 。
  • TrLaplace: “Do not come here! Food poisoning alert!” (别来这里！食物中毒警报！——负面情感) 。

拉普拉斯机制完全翻转了情感，这对效用来说是灾难性的。即使在严格的隐私限制下，TrLaplace 也保留了原本的含义。

结论与启示

论文 《Private Language Models via Truncated Laplacian Mechanism》 在隐私保护 NLP 领域迈出了重要的一步。通过解决将截断分布扩展到高维空间的数学挑战，作者创建了一种机制，该机制:

  1. 降低方差: 在数学上保证比标准方法增加更少的噪声误差。
  2. 保留语义: 保持句子可读并保留其原始情感。
  3. 维持严格隐私: 遵守 \((\epsilon, \delta)\)-差分隐私的严格定义。

对于 AI 领域的学生和从业者来说，这项工作强调了一个重要的教训: 面对复杂的高维数据，标准工具 (如基本的拉普拉斯噪声) 往往是不够的。 根据数据的几何形状定制数学机制——在本例中，通过截断和限制嵌入空间——可以在不牺牲隐私的情况下获得巨大的效用收益。随着我们继续构建处理敏感用户数据的 LLM，像高维截断拉普拉斯这样的技术可能会成为负责任 AI 工具箱中的重要组成部分。