大型语言模型 (LLMs) 的发展正受到一个巨大的限制: 规模。为了让模型更智能,它们变得越来越大,这使得针对特定任务对它们进行微调在计算上变得极其昂贵。
为了解决这个问题,社区采用了参数高效微调 (PEFT) 方法,其中 LoRA (低秩适应) 是其中的明星技术。LoRA 冻结了庞大的预训练模型,并注入微小的、可训练的适配器。它效果显著,但也有上限。由于 LoRA 的参数非常少,它们有时难以捕捉复杂的新行为。
这时就轮到混合专家模型 (MoE) 登场了。通过将 LoRA 与 MoE 结合,我们可以在每一层拥有多个 LoRA 适配器,并动态地将 token 路由到最合适的那个适配器上。这让我们两全其美: 高容量和低训练成本。
但这里有个问题。我们在每一层应该放多少个 LoRA 专家?标准方法只是瞎猜。它们给每一层分配相同数量 (例如 4 个) 的专家。
一篇名为 AlphaLoRA 的新论文指出,这种“平均主义”方法存在根本缺陷,因为神经网络中的层并非生而平等。有些层更“聪明” (训练得更好) ,需要的帮助较少。通过使用先进的谱理论来分析每一层的质量,AlphaLoRA 提出了一种无需训练的方法,可以将专家分配到最需要他们的地方。
在这篇文章中,我们将解构 AlphaLoRA,探索它如何利用权重矩阵的形状来自动优化模型架构。
背景: LoRA-MoE 的现状
在深入探讨新方法之前,让我们简要建立一下基线。
LoRA 和 MoE
在标准的 Transformer 块中,我们有稠密的前馈网络。 LoRA 通过添加一条包含两个较小矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\) 的并行路径,绕过了更新这些庞大稠密权重 (\(\mathbf{W}_0\)) 的需求。更新公式表示为:
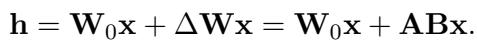
这允许我们通过仅更新 \(\mathbf{A}\) 和 \(\mathbf{B}\) 来微调模型。
LoRA-MoE 更进一步。我们不再只有一对 \(\mathbf{A}\) 和 \(\mathbf{B}\),而是创建多对 (即专家) 。一个“路由器 (Router) ”网络决定哪个专家处理特定的 token。如下所示:
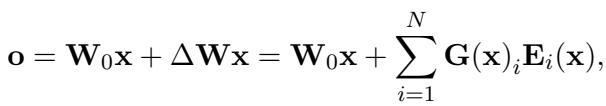
在这里,\(\mathbf{G}(\mathbf{x})_i\) 是路由器分配给第 \(i\) 个专家的门控分数 (概率) 。
均匀性问题
大多数当前的实现 (如 LoRAMoE 或 MixLoRA) 只是简单地为每一层分配 \(N\) 个专家。例如,第 1 层有 4 个专家,第 32 层也有 4 个专家。
然而,最近的研究表明深度神经网络存在冗余 。 并非每个参数都在做有用的工作。有些层在预训练期间学到了稳健的特征,而其他层则仍然“训练不足”或不稳定。如果一个层的质量已经很高,给它 8 个不同的 LoRA 专家就是浪费。相反,如果一个层很吃力,却被限制在与强层相同数量的专家上,它可能会因资源不足而受限。
以前解决这个问题的尝试,比如 MoLA , 尝试了手动启发式方法——给高层分配更多的专家 (三角形) 。但这仍然基于直觉,而非严谨的理论。
核心方法: AlphaLoRA
AlphaLoRA 这种方法背后的研究人员提出了一个问题: 我们能否从数学上衡量一个层的“训练完善程度”,并据此分配专家?
为了回答这个问题,他们转向了 重尾自正则化 (HT-SR) 理论 。
1. 用 HT-SR 诊断层的健康状况
这是论文中最迷人的部分。HT-SR 理论来自随机矩阵理论领域。它假设训练良好的神经网络的相关矩阵在其特征值中表现出重尾 (HT) 结构。
可以这样理解:
- 训练良好的层: 权重高度相关且有组织。它们的特征值分布 (经验谱密度,或 ESD) 具有特定的形状——“重尾”。这表明该层已经捕捉到了强大的特征。
- 训练不足的层: 权重更加随机或各向同性。它们尚未收敛到稳固的结构。
作者使用了一个名为 PL_Alpha_Hill 的指标。该指标将幂律拟合到层权重的特征值上。
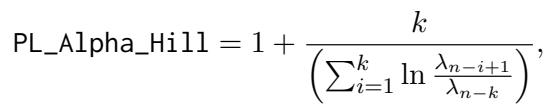
直觉是:
- 较低的
PL_Alpha_Hill值表示尾部更“重”。这意味着该层训练良好且稳定。它需要较少的 LoRA 专家来适应。 - 较高的
PL_Alpha_Hill值表示尾部较弱。这意味着该层训练不足 。 它需要更多的 LoRA 专家来帮助它在微调期间学习新特征。
作者使用该指标分析了 LLaMA 和 Mistral 等标准模型。
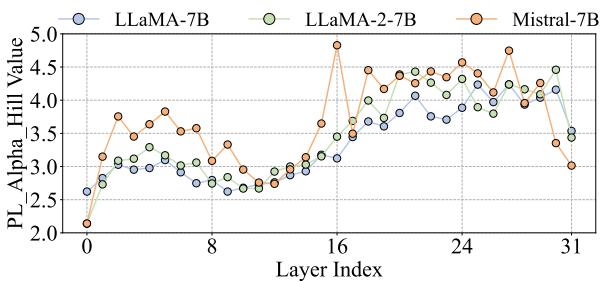
如上图 2 所示,质量差异巨大!它不是一条平线,也不是简单的线性递进。它是波动的,这意味着专家的均匀分配在数学上肯定也是低效的。
2. AlphaLoRA 流程
AlphaLoRA 是一个两步过程。至关重要的是,它是免训练的。你不需要运行预热训练来寻找架构;你只需分析预训练模型的静态权重。
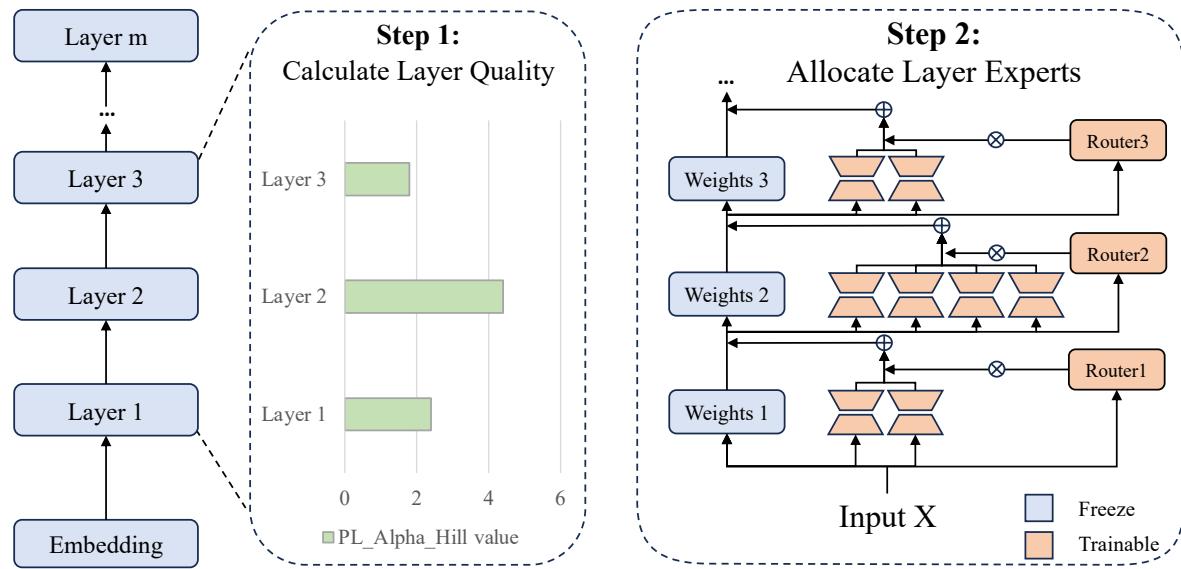
第一步: 计算层质量
对于模型中的每一层 \(i\),他们计算 PL_Alpha_Hill 值 (\(v_i\)) 。这给了他们一张模型的“体检表”,识别出哪些层强,哪些层弱。
第二步: 分配专家
他们将这些指标值转换为专家的整数计数。逻辑很简单: 根据 PL_Alpha_Hill 值成比例地分配专家。
映射函数定义为:
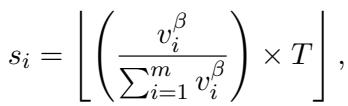
其中:
- \(v_i\) 是第 \(i\) 层的指标值。
- \(T\) 是整个模型允许的专家总数 (预算约束) 。
- \(\beta\) 是一个超参数,用于控制变化的激进程度。
由于专家必须是整数 (你不能有 2.5 个专家) ,他们会对结果进行四舍五入。如果四舍五入导致总计数与目标 \(T\) 略有偏差,他们会使用贪婪调整法,在四舍五入误差最大的地方增加或减少专家。
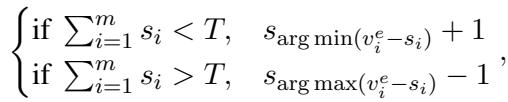
3. 最终架构
一旦分配完成,模型就被初始化了。训练不足的层可能会得到 8 或 10 个专家。训练良好的层可能只得到 1 或 2 个。
第 \(i\) 层中特定子模块 \(t\) 的前向传播看起来像标准的 LoRA-MoE,但可供选择的专家数量 (\(K\)) 是自定义的:
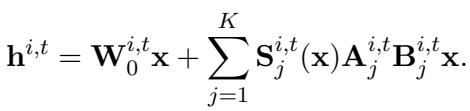
实验与结果
理论听起来很扎实,但在实践中有效吗?作者在 LLaMA-7B、LLaMA-2-7B 和 Mistral-7B 上测试了 AlphaLoRA,涵盖了各种任务,包括 GLUE (语言理解) 、推理基准和数学问题。
可视化“M”字形
最引人注目的结果是专家分配的可视化。记住,以前的方法使用“均匀” (平线) 或“三角形” (递增) 策略。AlphaLoRA 自然地发现了一种完全不同的模式。
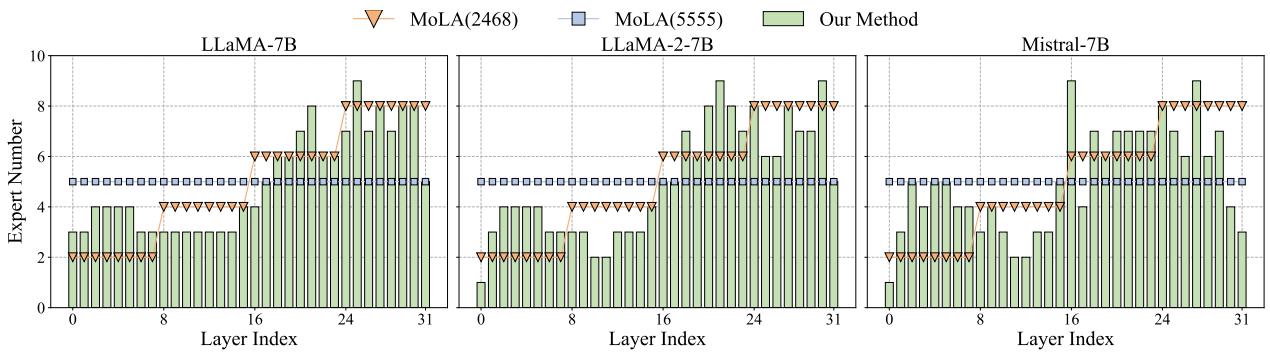
看看上面的图 3 (绿色条形) 。分配大致形成了一个 “M”字形 :
- 低层: 适量的专家。
- 中间层: 非常少的专家 (图 2 中的低
PL_Alpha_Hill值意味着这些层训练得很好) 。 - 高层: 许多专家。
这表明 LLaMA 和 Mistral 模型的中间层最为稳健,而最初和最后的层需要最多的适应。AlphaLoRA 自动发现了这一见解。
NLP 任务上的表现
作者将 AlphaLoRA 与 MoLA (最先进的基线) 进行了比较。他们测试了两种 MoLA 变体:
- 均匀 (Uniform) : 到处都是相同的专家 (例如 5555) 。
- 三角形 (Triangle, \(\nabla\)) : 专家数量递增 (例如 2468) 。
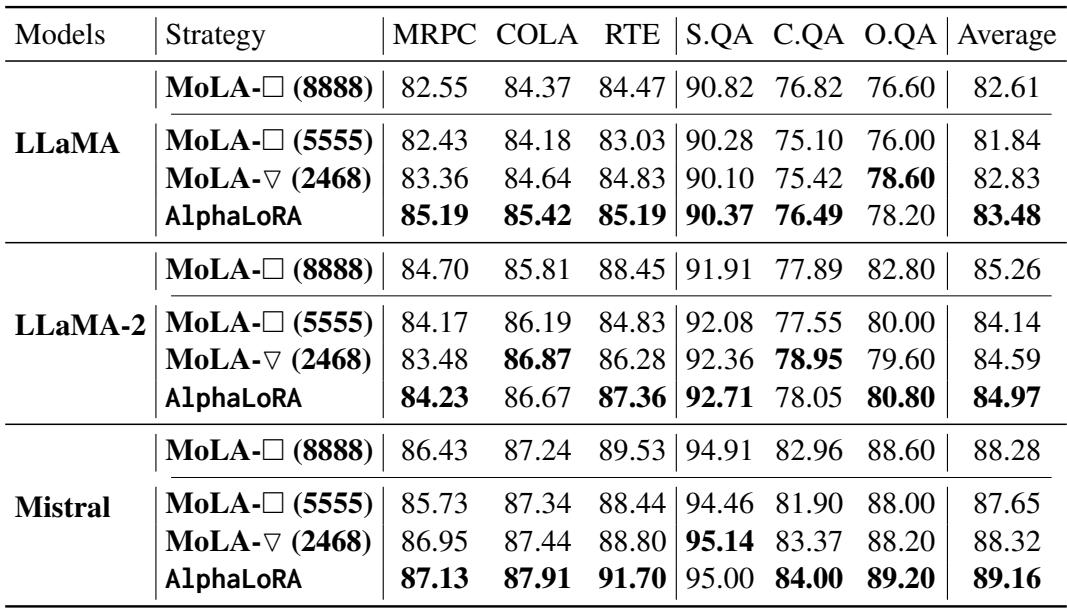
在表 2 中,AlphaLoRA 始终优于基线。
- 参数效率: 使用 160 个总专家的 AlphaLoRA (绿色行) 通常能匹配或击败使用 256 个专家的重型“8888”基线。
- 正面对决: 在相同的参数预算 (160 个专家) 下,AlphaLoRA 击败了手动的“三角形”策略 (MoLA-\(\nabla\)) 。
零样本推理
团队还测试了这些模型的泛化能力。他们在数学数据集 (MetaMathQA) 上微调模型,然后在未见过的数学问题 (GSM8K, SVAMP 等) 上进行测试。
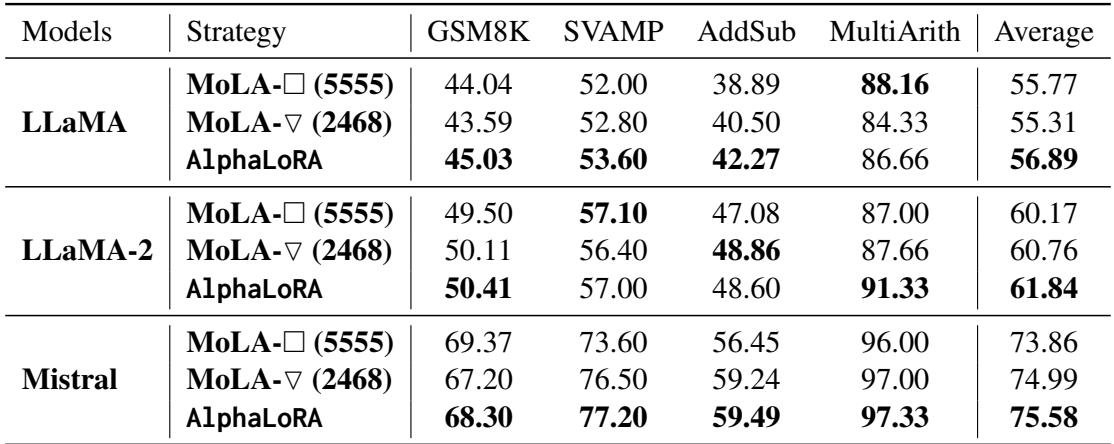
如表 3 所示,自适应分配在推理能力上提供了明显的提升,这表明把参数放在需要的地方比把它们摊薄能帮助模型更好地泛化。
少即是多
对于计算资源有限的学生和研究人员来说,最震撼的发现可能是效率的扩展性。作者测试了当限制专家总预算 (\(T\)) 时模型的表现。
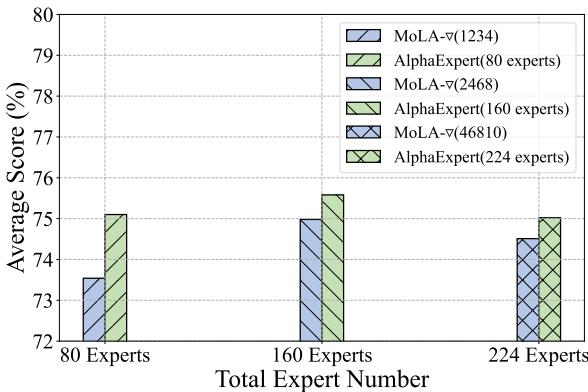
图 5 揭示了一个惊人的结果: 仅有 80 个专家的 AlphaLoRA 胜过了拥有 160 个专家的 MoLA。 通过智能地放置专家,你可以将模型增加的参数减半,却仍能获得更好的性能。
结论
AlphaLoRA 代表了从启发式深度学习设计向有理论依据的架构搜索的转变。它不再问“我们应该使用多少个专家?”,而是问“模型需要什么?”。
通过利用 HT-SR 理论 , AlphaLoRA 逐层诊断预训练模型。它识别出中间层通常是稳健且训练良好的,而外围层渴望适应。由此产生的“M 形”分配不太可能是人类设计者能猜到的,但它却产生了卓越的结果。
对于学生和从业者来说,要点很明确:
- 冗余是真实的: 均匀地向每一层添加参数是低效的。
- 预训练权重包含线索: 你可以分析模型的静态权重来确定如何最好地微调它。
- 自适应更好: 像 AlphaLoRA 这样的方法允许我们在更小的参数预算下榨取更多的性能,使 LLM 微调更加触手可及。
AlphaLoRA 的代码已经开源,提供了一种即插即用的方法来升级你的 MoE 微调流程,而无需昂贵的架构搜索步骤。
](https://deep-paper.org/en/paper/2410.10054/images/cover.png)