简介

我们经常把大型语言模型 (LLM) 当作全知全能的推理引擎。我们给它们输入复杂的情景、法律文件或医疗摘要，并要求它们得出结论。但是，当答案并非非黑即白时，这些模型的表现究竟如何呢？

在现实世界中，确定性是一种奢侈品。医生不会说“这个症状总是意味着 X”。他们会说，“考虑到这个症状，诊断结果极有可能是 X，除非同时也存在 Y。”这就是概率推理——一种处理不确定性、权衡证据并更新信念的能力。

最近一篇题为 “QUITE: Quantifying Uncertainty in Natural Language Text in Bayesian Reasoning Scenarios” (QUITE: 贝叶斯推理场景中自然语言文本的不确定性量化) 的论文研究了这一确切的能力。研究人员创建了一个具有挑战性的数据集，以测试 LLM 是否真的能够进行概率推理，还是仅仅在模仿逻辑模式。

研究发现令人大开眼界: 虽然 LLM 能言善辩，但它们执行复杂概率推理的能力——尤其是“反向”推理——极其有限。然而，该论文也提供了一个解决方案: 一种神经符号 (neuro-symbolic) 方法，它将 LLM 的语言流畅性与概率编程的严谨逻辑结合在了一起。

背景: 贝叶斯网络与我们要如何推理

为了理解这一挑战，我们首先需要了解科学家用来为这些问题建模的工具: 贝叶斯网络 (Bayesian Network) 。

贝叶斯网络是一个图，其中节点代表随机变量 (事件) ，箭头代表依赖关系 (概率) 。例如，“下雨”会影响“草地湿润”。与这些节点相关联的是概率表，它们确切地告诉我们，在给定父节点的情况下，某个事件发生的可能性有多大。

该论文确定了我们对这些网络执行的三种不同类型的推理，如下图所示:

Figure 2: Example instances of QUITE. Each question is categorized according to the reasoning pattern.

  1. 因果推理 (前向) : 我们观察原因并预测结果。
  • *示例: * 你看到一个司机有“喜欢冒险”的行为 (原因) 。发生事故的概率是多少 (结果) ？
  • *现状: * 人类和机器通常觉得这很直观。
  1. 证据推理 (后向) : 我们观察结果并推断原因。
  • *示例: * 你看到一辆车有防抱死制动系统 (结果) 。车主是风险规避者的概率是多少 (原因) ？
  • *现状: * 这需要应用贝叶斯定理来“反转”概率。这在计算上更难。
  1. 消除解释 (Explaining-Away) : 当两个独立的原因共享一个共同的结果时，就会发生这种情况。
  • *示例: * “轻微事故” (结果) 可能是由“驾驶技术差”或“天气恶劣”造成的。如果我们得知天气非常糟糕，那么司机技术差的概率就会下降 (天气“消除”了对事故的其他解释) 。
  • *现状: *这是一种复杂的认知飞跃，需要理解多个变量之间的相互作用。

当前基准测试存在的问题

以前测试 LLM 执行这些任务的尝试都太简单了。它们通常使用:

  • 仅限二元变量: (真/假) 。现实生活是有类别的 (高/中/低) 。
  • 仅限数字输入: “有 70% 的机会。” 现实中人类使用的是语言。
  • 简单的模板: 看起来像代码的句子，LLM 很 容易利用这一点。

QUITE 数据集 (Quantifying Uncertainty in Natural Language Text，量化自然语言文本中的不确定性) 改变了这一点。它使用来自医学和汽车保险等领域的真实网络，包含分类变量，并且关键是引入了估测概率词 (Words of Estimative Probability, WEPs) 。

估测概率词 (WEPs)

在自然对话中，我们很少用精确的百分比说话。我们会使用“可能 (likely) ”、“不太可能 (improbable) ”或“几乎确定 (almost certain) ”等词语。为了模拟这一点，研究人员根据人类感知研究将概率映射到了特定的副词。

Table 5: The mapping of WEP to numeric probabilities by Fagen-Ulmschneider (2015) that we use to model uncertainty on the Bayesian networks in our dataset.

这增加了一层难度: 模型必须首先解释语言上的细微差别 (“better than even” \(\approx\) 60%) ，然后才能尝试数学推理。

QUITE 数据集的构建

研究人员通过将已有的贝叶斯网络语言化来构建 QUITE。他们不仅使用模板；他们使用 LLM (特别是 Mixtral) 来生成丰富、多样的自然语言描述，以表达关系和概率。

生成流程确保了文本能够准确反映原始网络中复杂的数学依赖关系。

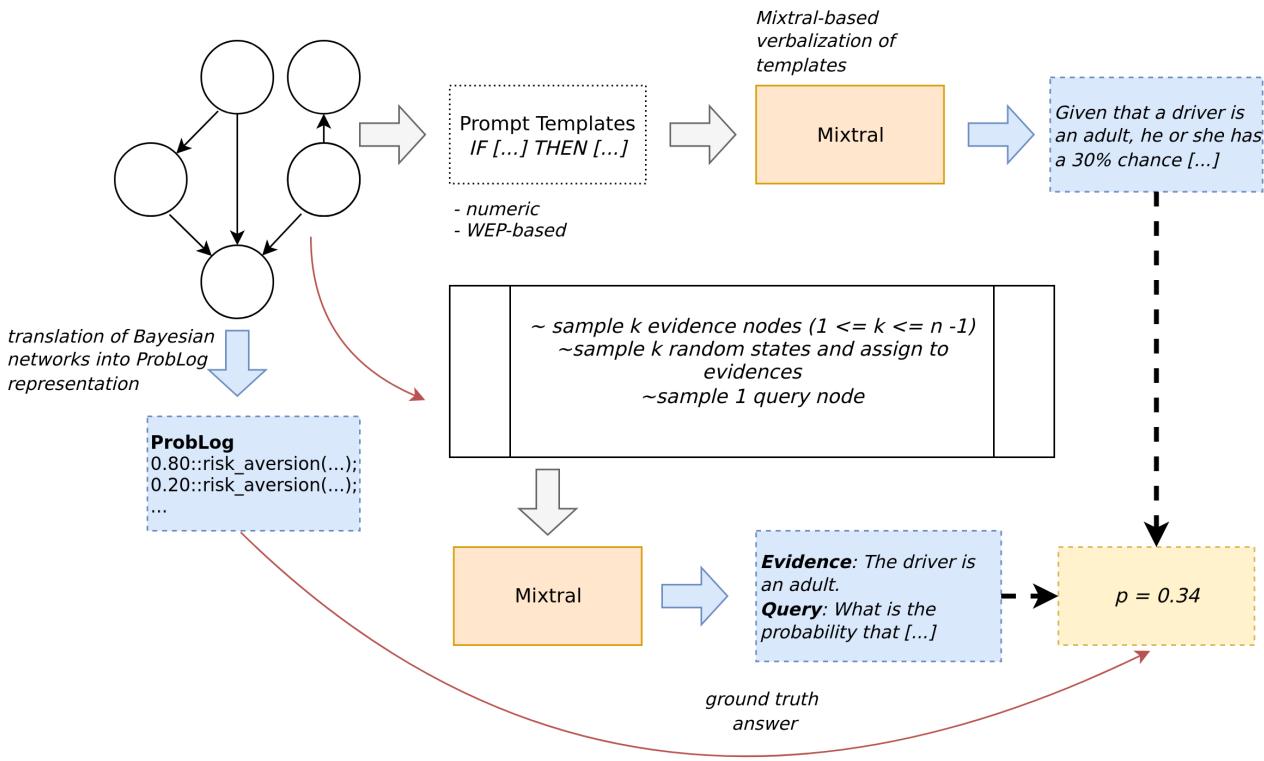
Figure 13: An schematic overview of our data generation pipeline.

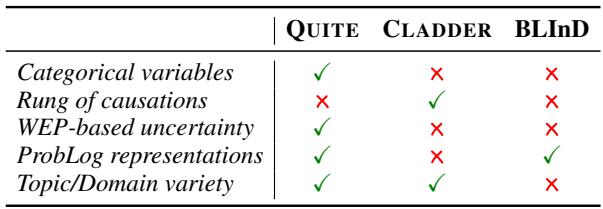
这一过程产生的数据集比 CLADDER 或 BLInD 等前辈更加复杂且语言更加多样化。如下面对比所示，QUITE 是唯一结合了分类变量、基于 WEP 的不确定性和 ProbLog 表示的基准测试。

Table 1: Comparison of QUITE, CLADDER,and BLInD.

核心方法: 神经符号 vs. LLM

该论文在解决这些推理问题的两种截然不同的方法之间展开了对决。

方法 1: 纯 LLM 提示

研究人员测试了 GPT-4、Llama-3 和 Mixtral 等模型。他们使用了:

  • 零样本 (Zero-Shot) : 简单地给模型文本并询问概率。
  • 因果思维链 (Causal Chain-of-Thought, CoT) : 要求模型“一步一步地思考”，写下变量，并执行计算。

方法 2: 神经符号方法

这是本文的新颖贡献。他们不要求 LLM 做数学题，而是要求 LLM 编写代码来表示数学题。

他们微调了一个 Mistral-7B 模型作为语义解析器 。 它的工作是读取自然语言前提 (例如，“如果病人有胆结石，就很可能出现胀气”) ，并将它们翻译成 ProbLog , 一种概率逻辑编程语言。

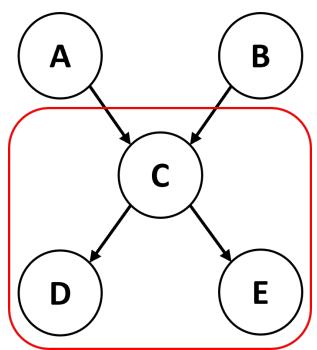
Figure 4: Full ProbLog code for the gallstone-flatulenceamylase instance. Figure 5: Example network for demonstrating our procedure of subsetting.

一旦文本被转换成如上图 (图 4) 所示的结构化代码，一个确定性的求解器就会执行该程序。这将“推理”和“计算”外包给了一个保证在数学上正确的系统，让 LLM 专注于它最擅长的事情: 理解语言。

深入探讨: 为什么数学很难

为了理解为何纯 LLM 举步维艰，让我们看看数据集中一个“简单”的证据推理查询所需的实际数学运算。

设想一个包含三个变量的网络: Gallstones (胆结石) , Flatulence (胀气) 和 Amylase (淀粉酶) 水平。 模型接收描述概率的文本。然后被问到: “假设病人有胀气，其淀粉酶水平在 500-1400 之间的可能性是多少？”

从数学上讲，我们需要计算:

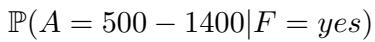
()\n\\mathbb { P } ( A = 5 0 0 - 1 4 0 0 | F = y e s )\n[

利用贝叶斯定理，这可以展开为:

]\n\\begin{array} { c l c r } { \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 | F = y e s ) } \\ { = \\frac { \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s ) } { \\mathbb { P } ( F = y e s ) } } \\end{array}\n[

问题在于分子 (上半部分) 并未在文本中直接给出。模型必须“边缘化 (marginalize out) ” Gallstones (胆结石) 变量。它必须将胆结石存在和不存在两种情况的概率相加:

]\n\\begin{array} { c } { { \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s ) } } \\ { { { } } } \\ { { { } = \\displaystyle \\sum _ { G } \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s , G ) } } \\ { { { } } } \\ { { { } = \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s , G = y e s ) } } \\ { { { } + \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s , G = n o ) } } \\end{array}\n[

然后，模型必须通过乘以隐藏在文本中的条件概率来找到这些值。对于存在胆结石的情况 (\(G=yes\)) :

]\n\\begin{array} { r l } & { \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s , G = y e s ) } \\ & { \\qquad = \\mathbb { P } ( F = y e s | G = y e s ) } \\ & { \\qquad \\cdot \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 | G = y e s ) } \\ & { \\qquad \\cdot \\mathbb { P } ( G = y e s ) } \\ & { = 0 . 3 9 2 5 \\cdot 0 . 0 1 8 7 \\cdot 0 . 1 5 3 1 \\approx 0 . 0 0 1 1 2 4 } \\end{array}\n[

对于不存在的情况 (\(G=no\)) :

]\n\\begin{array} { r } { \\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s , G = n o ) } \\ { = 0 . 4 3 0 7 \\cdot 0 . 0 1 0 1 \\cdot 0 . 8 4 6 9 \\approx 0 . 0 0 3 6 8 4 } \\end{array}\n[

将两者相加得到分子:

]\n\\mathbb { P } ( A = 5 0 0 - 1 4 0 0 , F = y e s ) \\approx 0 . 0 0 4 8 0 8\n[

但我们还没做完。我们仍然需要分母: 胀气的总概率 (\(P(F=yes)\)) 。这需要对胆结石和淀粉酶的所有状态进行边缘化。因为淀粉酶是分类变量，有 3 种状态，而胆结石是二元的，所以有 \(2 \times 3 = 6\) 种组合需要相加！

]\n\\begin{array} { c } { { \\mathbb { P } ( F = y e s ) } } \\ { { = \\displaystyle \\sum _ { G , A } \\mathbb { P } ( F = y e s , G , A ) } } \\end{array}\n[

![] = \mathbb { P } ( F = y e s , G = y e s , A = 0 - 2 9 9 )

\[](images/021.jpg#center) ![\]
  • \mathbb { P } ( F = y e s , G = y e s , A = 3 0 0 - 4 9 9 ) [](images/022.jpg#center)
  • (…加上另外 4 项…) *

最后，我们将分子除以分母得到最终答案:

]\n\\mathbb { P } ( A = 5 0 0 - 1 4 0 0 | F = y e s ) = { \\frac { 0 . 0 0 4 8 0 8 } { 0 . 4 2 4 8 5 6 } }\n()

结论: 这就是大量的算术上下文管理。期望 LLM 将所有这些数字保留在“脑子”里，完美地执行浮点乘法，并在没有计算器的情况下正确求和，这注定会失败。神经符号方法通过简单地将逻辑写入代码并让计算机处理数学运算，完全避免了这个问题。

实验与结果

那么，它们的对比结果如何呢？结果证实，标准的 LLM，即使是像 GPT-4 这样强大的模型，也不是可靠的概率推理器。

反向推理的失败

最引人注目的结果是按推理类型细分的性能崩溃。

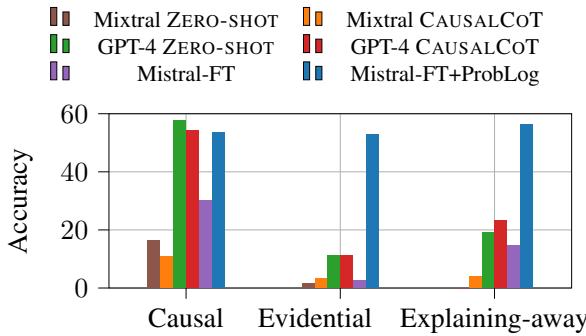
Figure 1: Percentage of instances solved correctly for each Bayesian reasoning type. The neuro-symbolic Mistral-FT+ProbLog approach is robust against the inherent difficulties of different reasoning types.

在上面的图 1 中，请看 Causal (因果) 列。GPT-4 (绿色/红色条) 表现尚可，准确率超过 50%。这是有道理的；从原因预测结果类似于文本生成的工作方式 (下一个 token 预测) 。

然而，看看 Evidential (证据) 和 Explaining-away (消除解释) 列。纯 LLM 方法崩溃了，准确率降至接近于零或非常低。它们无法有效地“逆转”因果流。

相比之下, Mistral-FT+ProbLog (蓝色条) 在所有三种类型中都保持稳健。因为它将问题转换为全局逻辑结构，推理的方向对求解器来说并不重要。它处理后向推理和前向推理一样容易。

错误分析: 复杂度很关键

研究人员还分析了导致模型失败的原因。不出所料，网络的大小 (上下文的数量) 起着巨大的作用。

对于神经符号模型 (ProbLog-FT) ，在较小的网络上表现出色，但随着文本变长 (需要解析的前提更多) ，性能会下降。

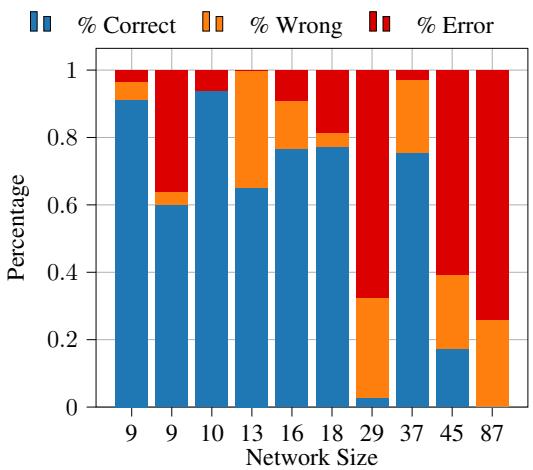
Figure 9: Results for Problog-FT for different network sizes.

然而，当我们查看纯 LLM 方法 (带有因果思维链的 GPT-4) 时，性能下降要严重和混乱得多。即使在中等规模下，错误率 (红色) 也会激增。

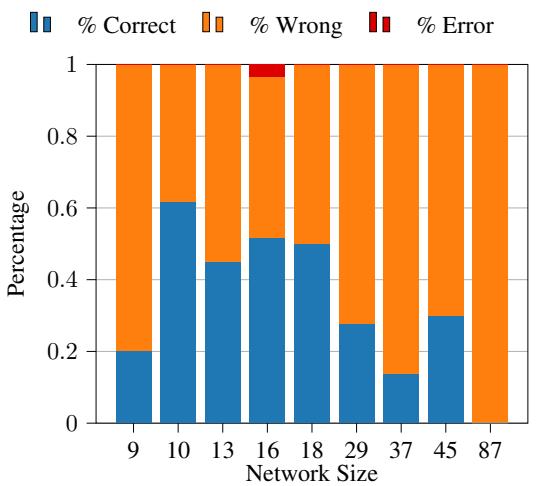
Figure 1O: Results for CausualCoT with GPT4 for different network sizes.

LLM 的主要错误是数学错误: 四舍五入错误、公式错误或仅仅是产生数字幻觉。神经符号方法的主要错误是解析错误: 生成了无效代码。有趣的是，一项“预言机 (oracle) ”实验表明，如果解析正确，答案就能保证是正确的。

结论

QUITE 论文是对大型语言模型推理能力的一次现实检验。它表明，虽然 LLM 理解因果关系的概念，但它们很难进行现实世界贝叶斯推理所需的严格、定量的既有不确定性的操作。它们在证据 (后向) 推理方面尤其糟糕，而在医疗诊断或调试等领域，这通常是我们最需要的。

这项工作强有力地支持了神经符号 AI (Neuro-symbolic AI) 。 通过使用 LLM 作为翻译器——将混乱、不确定的自然语言转换为干净、结构化的代码——并使用经典求解器来处理繁重的工作，我们可以构建既灵活又逻辑严密的系统。

随着我们的前进，通往更智能 AI 的道路可能不是更大的语言模型，而是知道如何使用计算器和逻辑求解器的语言模型。