集成幻觉: 为何深度集成可能只是伪装的大模型

在机器学习的经典时代，“集成 (ensembling) ”是最接近免费午餐的东西。如果你训练单个决策树，它可能会过拟合。但如果你训练一百棵树并对它们的预测取平均值 (随机森林) ，你会得到一个鲁棒且高精度的模型。直觉很简单: 不同的模型会犯不同的错误，所以将它们平均起来可以抵消噪声。

然而，现代深度学习在一种完全不同的机制下运作: 过参数化 (overparameterization) 。 我们现在通常使用参数数量远多于训练数据点的神经网络。有趣的是，从业者仍然使用集成 (深度集成) ，声称它们能提高准确性并提供更好的不确定性估计。

但是，旧的直觉在这个新世界中还成立吗？

最近的一篇论文《Theoretical Limitations of Ensembles in the Age of Overparameterization》 (过参数化时代集成的理论局限性) 挑战了传统观念。作者认为，在过参数化机制下，集成并不具备像在经典机器学习中那样神奇的方差缩减特性。相反，过参数化模型的无限集成在数学上等价于单个更大的模型。

在这篇文章中，我们将拆解这篇论文，探讨为何向集成中添加更多模型实际上可能等同于只是让你的单个模型变得更宽。

转变: 从欠参数化到过参数化

要理解作者的论点，我们首先必须区分机器学习的两种机制。

  1. 欠参数化 (经典) : 你的数据多于参数 (例如，在高瘦数据集上进行线性回归) 。模型无法完美拟合训练数据 (训练误差非零) 。在这里，集成通过减少方差和稳定预测来提供帮助。
  2. 过参数化 (现代) : 你的参数多于数据 (例如，深度神经网络) 。模型有足够的容量完美记忆整个训练集 (训练误差为零) 。

作者使用 随机特征 (Random Feature, RF) 模型 作为代理来研究这个问题。RF 模型是神经网络的一种易于处理的近似形式。RF 模型固定隐藏层的权重，仅训练最后的线性层。

这篇论文的核心问题是: 在相同数据上训练的过参数化模型集成，其泛化能力是否优于单个非常大的模型?

核心等价性

该论文最重要的理论贡献是证明了，在极少的假设下，过参数化模型的 无限集成 与 单个无限宽模型 会做出完全相同的预测。

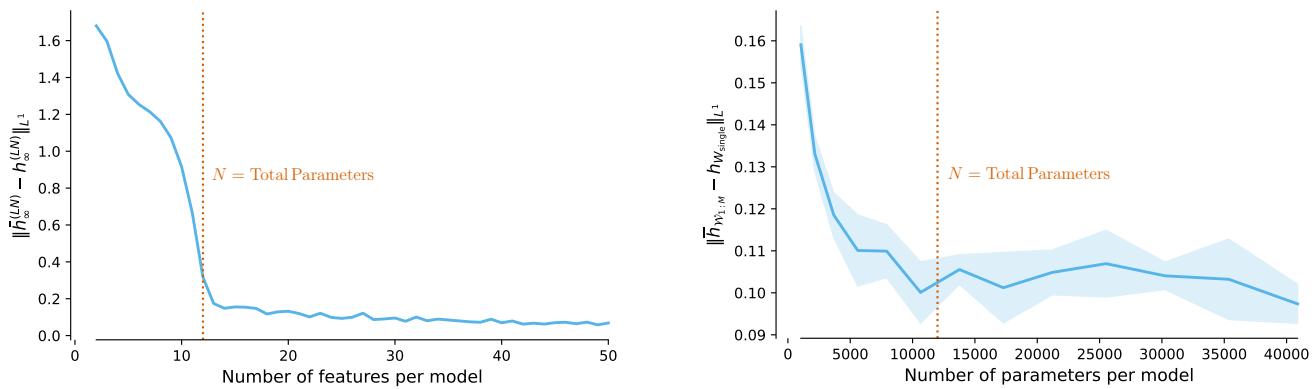
等价性的可视化

让我们看看随机特征模型的表现。在下图中，左侧面板显示了在简单数据集上训练的 100 个独立的有限宽度模型 (蓝线) 。它们的表现差异很大。然而，右侧面板显示了当你平均 10,000 个这样的模型 (一个“无限”集成) 时会发生什么。

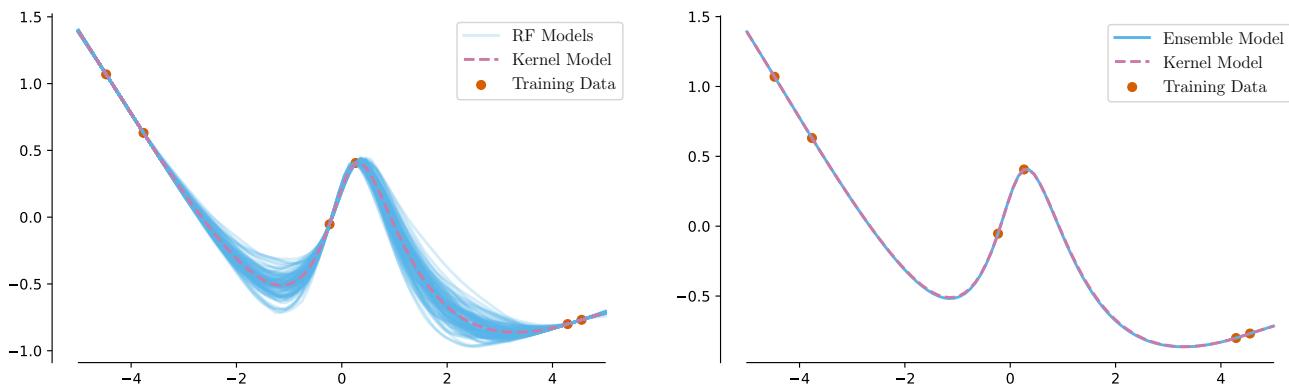
图 1: 单个 RF 模型与集成的比较。

正如你在右侧面板中看到的，集成预测 (蓝色) 变得与单个无限宽模型 (粉色) 难以区分。作者证明了这并非巧合——这是一个数学恒等式。

等价性的数学原理

为了证明这一点，作者分析了“无岭 (Ridgeless) ”最小范数 (LN) 预测器。当一个模型过参数化时，有无限多个解可以完美拟合数据。“最小范数”解是那些在拟合数据的同时保持权重尽可能小的解 (这正是梯度下降倾向于找到的解) 。

具有随机特征 \(\mathcal{W}\) 的单个模型的预测表示为 \(h_{\mathcal{W}}^{(\mathrm{LN})}\)。随着宽度 \(D\) 趋于无穷大，这个单个模型收敛到一个核预测器:

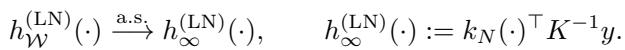
展示单个模型收敛到核极限的公式。

现在，考虑一个 集成 。 集成是对许多此类模型的预测取平均值。作者推导出了无限集成预测 \(\bar{h}_{\infty}^{(LN)}(x^*)\) 的分解，如下所示:

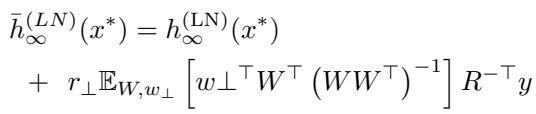
无限集成预测的分解。

这个公式比较复杂，让我们分解一下:

  1. 第一项: \(h_{\infty}^{(LN)}(x^*)\) 是单个无限宽模型的预测。
  2. 第二项: 公式的第二部分 (以 \(r_\perp\) 开头) 代表集成与单个无限模型之间的 差异。

变量 \(W\) 代表投影到训练数据上的随机特征，而 \(w_\perp\) 代表正交于数据的特征分量。

关键证明: 作者证明了第二项中的期望值是 零 (在关于特征分布的温和假设下) 。

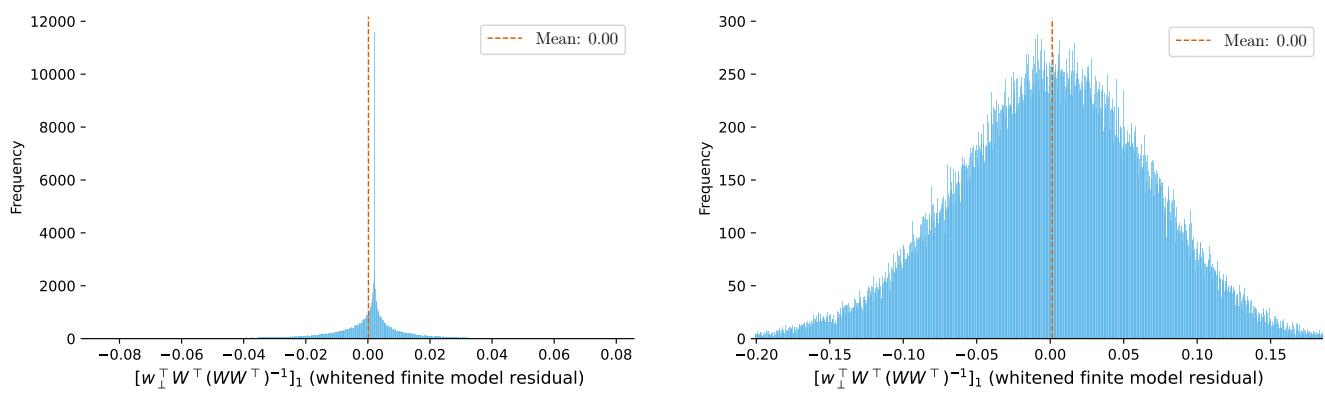
以零为中心的误差项的经验分布。

上面的直方图 (图 12) 经验性地验证了这一证明。无论使用 ReLU 还是高斯误差特征，误差项都完美地分布在零周围。

结论: 由于误差项消失，无限集成的预测与单个无限宽模型的预测是 *逐点等价 (pointwise equivalent) * 的。集成并没有增加单个巨型模型所不具备的任何“新”函数空间覆盖。

有限预算: 集成与巨型模型

你可能会反驳说，“我无法训练一个无限宽的模型。我有内存预算限制。”

研究人员通过比较两个具有相同总参数预算的实际设置来解决这个问题:

  1. 集成: \(M\) 个模型，每个有 \(D\) 个特征。
  2. 单个大模型: 1 个模型，有 \(M \times D\) 个特征。

如果经典直觉成立，集成应该具有更好的泛化能力。然而，论文推导出的理论界限表明情况并非如此:

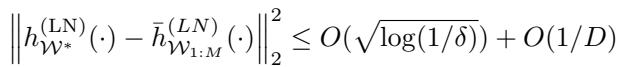
单个大模型与集成之间差异的理论界限。

该不等式表明，单个大模型与集成之间的平方差与 \(O(1/D)\) 成比例。随着集成中的单个模型变得足够过参数化 (\(D\) 很大) ，集成与单个巨型模型变得几乎完全相同。

实证结果

作者在随机特征模型和真实的神经网络 (MLP) 上对此进行了测试。

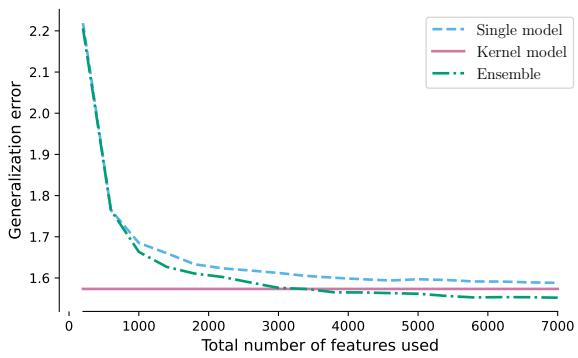
RF 和神经网络的泛化误差缩放。

在上面的图 3 中:

  • 左图 (RF 模型) : 随着特征数量的增加，绿线 (集成) 和浅蓝线 (单个大模型) 几乎完美重合。
  • 右图 (神经网络) : 出现了相同的趋势。当总参数数量固定时，集成相比单个大模型并没有提供显著的泛化优势。

这产生了一个“曲棍球棒”模式 (下图 2) ，即当模型很小 (欠参数化) 时，两种方法之间的差异很大，但一旦模型变得过参数化 (\(D > N\)) ，差异就缩小为零。

显示集成和单个模型收敛的曲棍球棒模式。

重新思考不确定性与方差

从业者使用深度集成的一个主要原因是为了 不确定性量化 。 逻辑是: “如果我的集成成员意见不一致 (高方差) ，那么模型就是不确定的。”

在贝叶斯统计中，方差通常与“认知不确定性 (epistemic uncertainty) ” (由于缺乏数据导致的不确定性) 相关。然而，作者表明，在过参数化机制下，集成方差衡量的是完全不同的东西。

方差方程

作者推导了集成的预测方差:

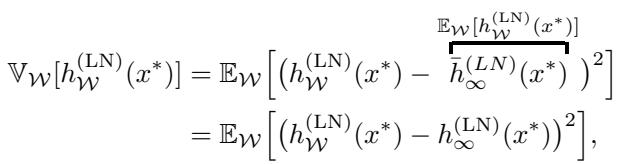
方差方程推导。

该方程表明，方差仅仅是有限宽度模型与无限宽度极限之间平方差的期望值。通俗地说: 集成方差量化的是，如果我们增加模型容量，预测值的预期变化。

它是对 参数化敏感性 的衡量，而不一定衡量你离训练数据有多远。

高斯陷阱

以前的理论工作假设随机特征是高斯的。如果你做这个假设，数学公式会简化为一个非常特定的形式:

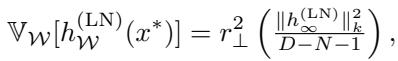
高斯假设下的方差。

在这个特定的高斯情况下，方差项 \(r_\perp^2\) (如下所示) 实际上 看起来确实 像贝叶斯高斯过程的后验方差。

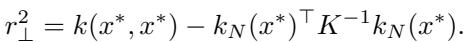
r-perp 平方的定义。

然而，神经网络特征 (如 ReLU) 不是 高斯的。当作者分析一般特征时，他们发现集成方差的行为与“理想的”贝叶斯不确定性大相径庭。

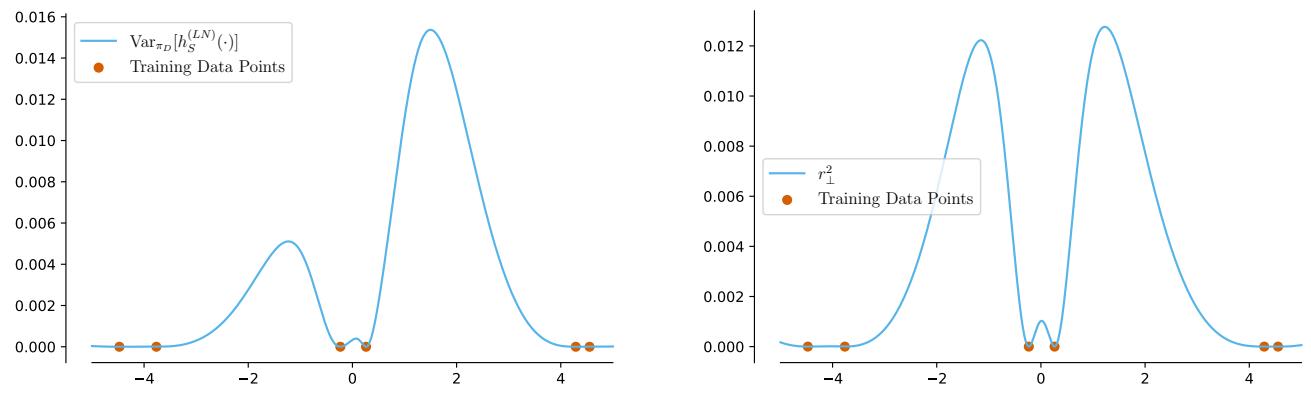
集成方差与贝叶斯不确定性的比较。

请看图 4 (上图) 。

  • 左图: 过参数化集成的实际方差。
  • 右图: “理想的”贝叶斯不确定性 (高斯过程后验) 。

它们看起来完全不同。峰值和波谷并不对齐。这表明，在安全关键型应用中，将深度集成方差作为“我不知道”的代理可能会产生误导。它并不能像高斯过程那样捕捉到与训练数据的距离。

对正则化的鲁棒性

上面的分析集中在“无岭”回归 (纯插值) 。如果我们添加正则化 (岭回归) ，这还成立吗？

作者证明这种过渡是平滑的。他们表明，集成与单个模型之间的差异关于岭参数 \(\lambda\) 是 利普希茨连续 (Lipschitz continuous) 的。

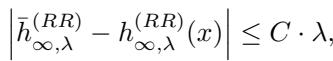
岭参数的利普希茨连续性。

这意味着对于小的正则化 (在深度学习中很常见) ，这种等价性仍然近似成立。当 \(\lambda \to 0\) 时，差异消失。

结论与启示

论文《Theoretical Limitations of Ensembles in the Age of Overparameterization》为深度学习从业者提供了一个发人深省的现实检验。

关键要点:

  1. “魔力”源于容量: 深度集成的性能提升主要来自于它们近似于一个更大的单个模型。如果你能直接训练那个更大的模型，你很可能会得到类似的结果。
  2. 泛化没有免费午餐: 一旦你的组件模型是过参数化的，集成并不会比具有相同总参数数量的单个模型提供根本性的泛化优势。
  3. 不确定性警示: 要小心将集成方差解释为“不确定性”。它主要衡量的是模型对其自身宽度/容量的敏感性，这可能与真实的认知不确定性 (模型不知道什么) 并不一致。

这是否意味着我们应该停止使用集成? 不一定。与并行训练 \(M\) 个较小的模型相比，训练一个巨大的模型往往更难 (优化困难) 或在计算上不可行 (内存限制) 。集成仍然是一个实用的 计算 技巧。

然而，我们应该停止将它们视为一种能在经典意义上提供“多样性”的独特统计方法。在过参数化时代，集成只是一种构建巨型神经网络的分布式方式。