为何随机采样还不够: 主动学习在求解 PDE 中的威力

如果你涉足过科学计算或物理机器学习领域，你一定熟悉这样的流程: 你有一个描述物理系统的偏微分方程 (PDE) ，比如热传导方程或纳维-斯托克斯方程。传统上，求解这些方程需要耗费大量计算资源的数值求解器。

算子学习 (Operator Learning) 应运而生。其目标是训练一个机器学习模型来近似 PDE 的“解算子”。与其每次从头开始求解方程，不如将初始条件或源项输入神经网络 (或其他估计器) ，它就能几乎瞬间输出解。

但这有个前提。训练这些模型需要数据——大量的输入-输出对。借鉴经典统计学习的标准方法是被动数据收集 (passive data collection) : 生成随机输入，运行昂贵的求解器得到输出，然后在该数据集上进行训练。

最近的一篇研究论文*《On the Benefits of Active Data Collection in Operator Learning》* (论算子学习中主动数据收集的益处) 提出了一个根本性的问题: 随机采样真的是学习这些算子的最佳方式吗?

答案是一个响亮的“不”。在这篇文章中，我们将深入探讨这篇论文，了解为何让学习者选择其数据 (主动学习) 相比传统的被动方法能带来指数级更快的收敛速度。

设定: 学习线性算子

要理解这一突破，我们需要先定义基础背景。我们关注的是由线性 PDE 控制的系统。

想象一个定义域 \(\mathcal{X}\) (比如一个方形板或 3D 盒子) 。我们有一个线性算子 \(\mathcal{F}\) (解算子) ，它将输入函数 \(f\) (源项) 映射到输出函数 \(u\) (解) 。

\[u = \mathcal{F}(f)\]

我们的目标是利用 \(n\) 个训练对 \(\{(f_j, u_j)\}_{j=1}^n\) 构建一个估计器 \(\widehat{\mathcal{F}}_n\)，使其能很好地近似真实算子 \(\mathcal{F}\)。“很好”通常意味着最小化 \(L^2\) 范数下的误差 (即函数的标准均方误差) 。

被动陷阱

在标准的“被动”设置中，我们假设输入函数 \(f\) 是从某个概率分布 \(\mu\) 中随机抽取的。我们训练模型，然后在从同一分布中抽取的具有新函数上进行测试。

我们试图最小化的误差如下所示:

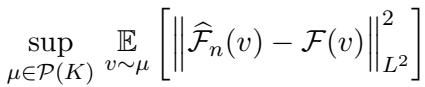
分布 mu 上的期望误差。

研究人员指出了这里的问题: 在被动学习的标准假设下，误差收敛速率通常停滞在 \(\approx n^{-1}\)。这意味着要将误差减半，你可能需要双倍的数据。当数据来自昂贵的数值求解器时，这是一个高昂的代价。

秘密武器: 协方差核

为了比随机采样做得更好，我们需要理解输入数据的结构。作者假设输入函数是从一个具有连续协方差核 (covariance kernel) \(K\) 的随机过程中抽取的。

如果你熟悉高斯过程，这听起来会很耳熟。核 \(K(x, y)\) 描述了点 \(x\) 和 \(y\) 处函数值之间的相关性。它本质上定义了我们预期看到的函数的“纹理”或“平滑度”。

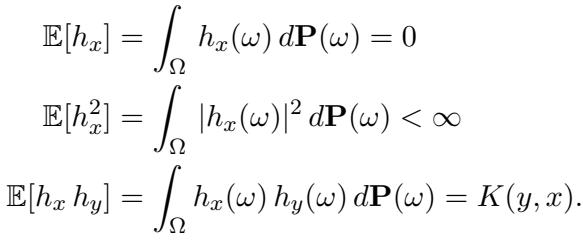
随机过程和核 K 的属性。

特征值与特征函数

这是线性代数发挥魔力的地方。任何连续核 \(K\) 都可以利用其特征对 (eigenpairs) \((\lambda_j, \varphi_j)\) 进行分解。

可以将这些特征函数 \(\varphi_j\) 想象成数据分布的“积木”或“基函数”，而特征值 \(\lambda_j\) 则是这些积木的“重要性权重”。

  • \(\varphi_1\) 是数据中最主要的形状。
  • \(\varphi_2\) 是第二主要的，依此类推。
  • 特征值通常会衰减: \(\lambda_1 \ge \lambda_2 \ge \dots \ge 0\)。

在数学上，它们满足以下积分方程:

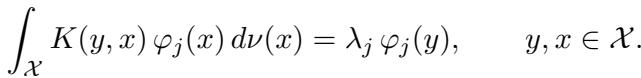
定义特征对的 Fredholm 积分方程。

由于这些输入来自 \(K\) 定义的随机过程，我们可以使用 Karhunen-Loève (KL) 展开来表示任何随机输入函数 \(v\)。这就像傅里叶级数，但它是专门针对我们要处理的数据的概率分布定制的:

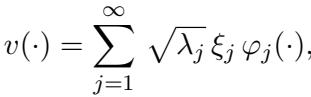
Karhunen-Loève 展开公式。

这里，\(\xi_j\) 是不相关的随机变量。这个公式告诉我们，任何输入函数都只是特征函数的加权和。

主动策略: 别靠猜，去查询！

在主动学习 (Active Learning) 中，学习者不必被迫接受随机数据。它可以构建一个特定的输入 \(v\)，并向“预言机 (Oracle) ” (即 PDE 求解器) 查询相应的输出。

如果你知道你的数据完全是由积木 \(\varphi_1, \varphi_2, \dots\) 构成的，你会向预言机问什么？

你不会问一个随机混乱的组合。 你会直接询问这些积木本身。

算法

作者提出了一个确定性的策略:

  1. 确定核 \(K\) (这意味着我们知道输入的分布) 。
  2. 计算特征函数 \(\varphi_1, \dots, \varphi_n\)，对应于最大的特征值。
  3. 查询预言机 , 使用这些特征函数作为输入。我们得到输出 \(w_i = \mathcal{O}(\varphi_i)\)。
  4. 构建估计器 :

估计器是直接由这些对构建的线性算子:

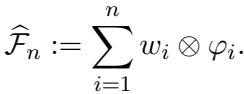
估计器定义。

这看起来像是一个张量积。实际上，这个算子的意思是: “如果我看到一个看起来像 \(\varphi_i\) 的函数，我就输出 \(w_i\)。”由于我们分布中的任何函数都是 \(\varphi_i\) 的和，这个估计器确切地知道如何处理数据中最重要的分量。

预言机并不完美

现实世界中的 PDE 求解器并不完美。它们存在离散化误差 (网格大小) 或数值容差。作者通过假设预言机是一个 \(\varepsilon\)-近似预言机来考虑这一点。

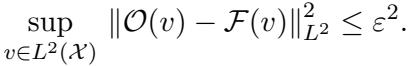
预言机误差界限 epsilon。

这个 \(\varepsilon\) 代表“不可约误差”——即我们训练数据的噪声底线。

理论突破: 任意快的收敛

这篇论文的主要贡献是证明了这种主动策略在很大程度上优于被动学习。

定理 1 (上界) 指出主动估计器的误差由两项界定:

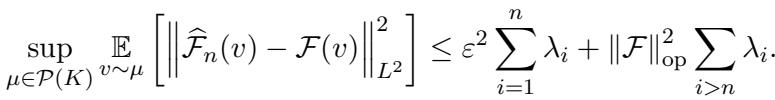
主要上界不等式。

让我们拆解一下:

  1. 不可约误差 (左项) : \(\varepsilon^2 \sum_{i=1}^n \lambda_i\)。这取决于你的 PDE 求解器的质量 (\(\varepsilon\)) 。如果你的求解器是完美的 (\(\varepsilon=0\)) ，这一项就会消失。
  2. 可约误差 (右项) : \(\|\mathcal{F}\|_{\mathrm{op}}^2 \sum_{i=n+1}^\infty \lambda_i\)。这是由于只采样了 \(n\) 个样本而停止所产生的误差。它取决于特征值的尾和。

这为什么很重要? 在被动学习中，无论你的数据多么平滑，你都被困在通过大约 \(n^{-1}\) 的收敛速率中。 在这种主动设置中，收敛速率取决于特征值 \(\lambda_i\) 衰减的速度。

  • 如果特征值呈指数级衰减, 误差也将呈指数级衰减。
  • 如果特征值呈多项式衰减 (\(n^{-k}\)) ，误差也会随之变化。

仅仅通过拥有一个特征值快速衰减的核，我们就可以实现任意快的速率。

收敛示例

作者提供了具体的例子来说明这一点:

1. 平移拉普拉斯核 (Shifted Laplacian Kernel) : 在 PDE 文献中很常见，这种核产生多项式衰减。在特定参数下，可约误差衰减为:

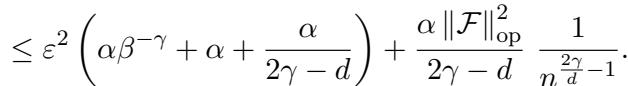
多项式衰减率示例。

2. RBF 核 (高斯) : 径向基函数 (Radial Basis Function) 核非常平滑。其特征值呈指数级衰减。因此，主动学习误差呈指数级消失:

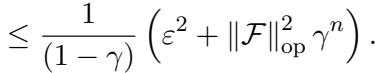
指数衰减率示例。

3. 布朗运动 (Brownian Motion) : 即使对于像布朗运动这样较粗糙的过程，误差也能很好地衰减:

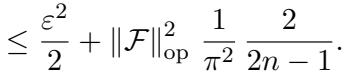
布朗运动的衰减率。

被动学习的局限性

你可能会问，“难道我就不能在被动学习中侥幸成功吗？”

作者证明了答案是否定的。 定理 2 为任何被动数据收集策略建立了一个下界。

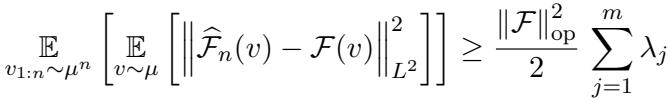
被动学习的下界。

即使拥有完美的预言机 (\(\varepsilon=0\)) 和无限的样本，被动学习也会从根本上受到估计方差的限制。论文构建了一个特定的“困难”分布，在该分布中被动学习者无法有效收敛，从而证明主动方法和被动方法之间的差距是理论上的，而不仅仅是实验上的。

实验证据

理论很好，但在实践中行得通吗？研究人员将他们的主动线性估计器与以下方法进行了对比:

  1. 被动线性估计器: 同样的数学原理，但在随机输入上进行训练。
  2. 傅里叶神经算子 (FNO) : 一种用于 PDE 的最先进深度学习模型，使用被动数据训练。

他们在两个经典问题上进行了实验: 泊松方程 (Poisson Equation) 和热传导方程 (Heat Equation) 。

泊松方程结果

实验设置涉及在 2D 网格上求解 \(-\nabla^2 u = f\)。

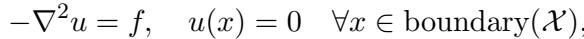
泊松方程定义。

使用的误差度量是相对 \(L^2\) 误差:

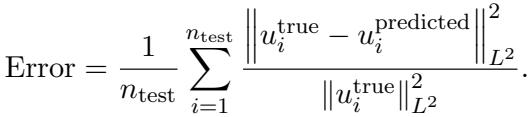
误差度量定义。

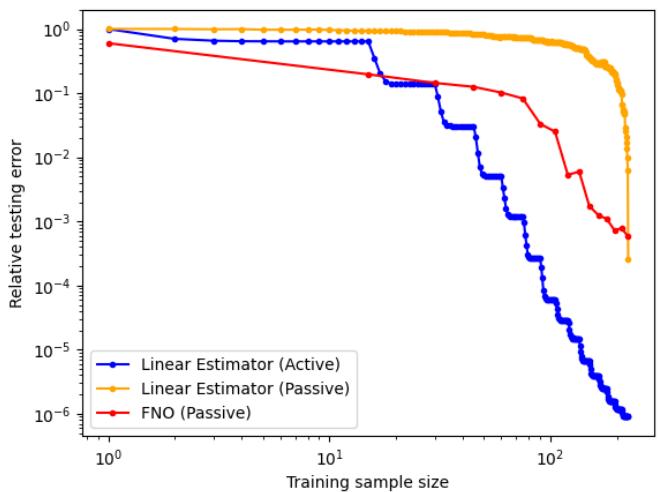
结果: 看下面的图表。蓝色曲线 (主动线性) 像石头一样急剧下降。橙色 (被动线性) 和红色 (FNO 被动) 则难以望其项背。

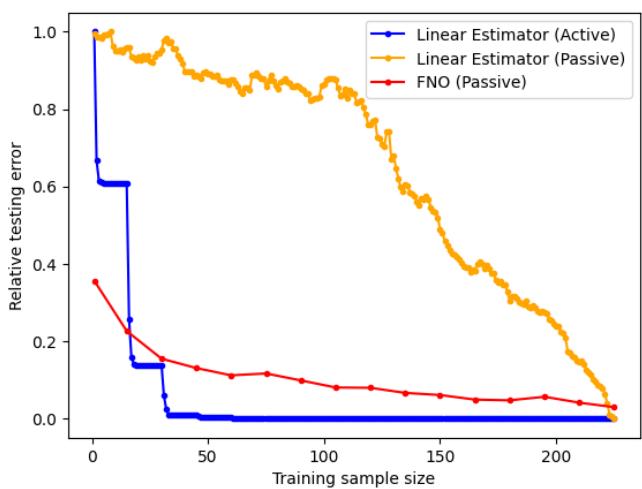
图 1: 泊松方程各种估计器的比较。

在双对数坐标 (log-log scale) 下观察，差异更加明显。在相同的训练样本数 (\(N\)) 下，主动线性估计器实现的误差比被动方法低了几个数量级。

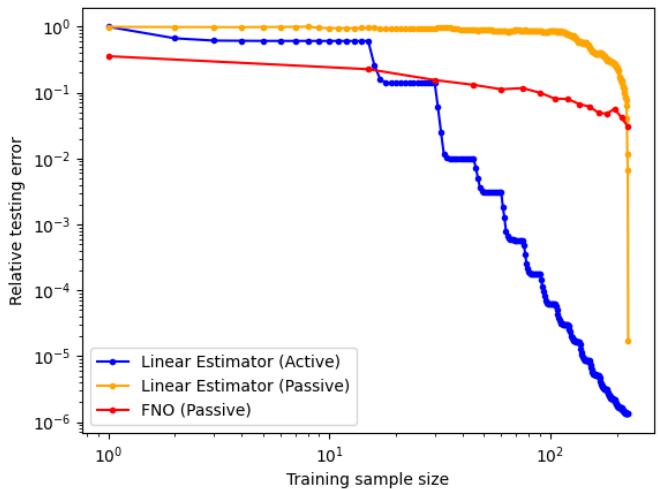
图 2: 双对数坐标下的泊松结果。

热传导方程结果

热传导方程也发现了类似的结果，该方程涉及时间演化。

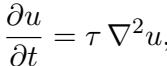
热传导方程定义。

同样，在对数坐标下，主动线性估计器 (蓝色) 显著优于被动变体。

图 4: 对数坐标下的热传导方程结果。

使用主动数据的 FNO 表现如何？

实验中一个有趣的旁注 (显示在论文附录中) 是，简单地将主动数据输入像 FNO 这样的深度学习模型并不能自动解决问题。FNO 是为从独立同分布 (i.i.d.) 样本中泛化而设计的。当输入高度结构化、非独立同分布的特征函数时，它的初始表现实际上更差，因为训练分布与测试分布不匹配。

这强调了主动学习需要估计器与策略相匹配。 线性估计器之所以有效，是因为它在数学设计上利用了特征函数的正交性。

结论与主要收获

这项研究为一个直观的观点提供了严格的数学基础: 信息比数量更重要。

通过分析数据的协方差结构 (核) ，我们可以识别函数空间的“主成分” (特征函数) 。向模拟器查询这些特定成分，使我们能够以比随机猜测少得多的样本重构解算子。

给学生和从业者的主要收获:

  1. 数据效率: 如果你的模拟很昂贵，不要只做随机采样。寻找主动策略。
  2. 了解你的核: 输入数据的平滑度和结构决定了你学习速度的理论上限。
  3. 线性的力量: 对于线性 PDE，简单的线性估计器结合智能的数据收集，可以胜过在“笨”数据上训练的复杂神经网络。
  4. “被动障碍”: 从随机样本中学习的速度有一个硬性限制 (\(\sim n^{-1}\)) 。主动学习是打破这一障碍的关键。

随着我们迈向数字孪生和实时物理模拟，像这样能从每一次昂贵计算中榨取最大信息的技术，将成为新的标准。