超越 MAML：一种利用核与梯度协调的更快、更智能的学会学习之道

引言: 对数据的渴求与学会学习的希望

深度学习已经彻底改变了从计算机视觉到自然语言处理的众多领域，但这一成功也伴随着高昂的代价。最先进的模型出了名地“嗜数据如命”，通常需要数百万个带标签的样本和庞大的计算资源来训练。那么，如果一个模型可以像人类一样，仅凭几个例子就掌握一项新技能，会怎样呢？这正是小样本学习 (few-shot learning) 的核心挑战。

为了解决这一问题，研究人员转向了元学习 (meta-learning)——一种常被描述为“学会学习”的范式。它的思路不是让模型掌握单一任务，而是让模型在大量任务上训练，从而学会如何用极少的数据快速适应新的、从未见过的挑战。

该领域中最具影响力的算法之一是模型无关元学习 (Model-Agnostic Meta-Learning, MAML) 。 它的优雅源于简洁: MAML 学习到一个优秀的初始化——即任何新任务的理想起点。基于这一初始化，模型只需几次梯度下降就能完成对新任务的微调。

然而，MAML 也存在不足。它依赖于两层嵌套的梯度下降循环——用于任务适应的内循环和用于元优化的外循环——这导致计算代价高昂、运行速度缓慢。此外，当训练任务差异过大时，MAML 的元更新可能变得不稳定，因为相互冲突的目标会让模型的优化方向分歧。

这正是近期论文《Fast Adaptation with Kernel and Gradient Based Meta Learning》的突破所在。它提出了一个名为函数空间中的自适应元学习 (Adaptive Meta-Learning in Functional Space, AMFS) 的强大双层框架，重新定义了内循环和外循环。其结果是一种更快、更稳定、理论上更丰富的方法。让我们看看 AMFS 是如何实现的。

背景: 理解 MAML 及其挑战

在深入 AMFS 之前，让我们先来拆解 MAML 的运作。想象你要训练一个可以识别鸟类的模型——但对于任何新物种，你只有五张图片。

MAML 通过一种称为情景式学习 (episodic learning) 的过程来解决这个问题，其中每个情景代表一个小型“任务”。

1. 内循环 (任务适应) : 对于每个任务，MAML 从当前的元参数集 \(\theta\) 开始。它在一个小样本集 (支持集) 上执行若干步梯度下降，得到任务特定的参数 \(\theta'\)。这种适应过程快速但迭代。

2. 外循环 (元优化) : 适应完成后，模型在同一任务的查询集上进行测试。得到的误差用于更新原始元参数 \(\theta\)。经过多个任务的训练，这些更新帮助 MAML 学到一个能够快速适应新数据的初始化。

这一优雅的框架让 MAML 在参数空间中找到一个“甜点区域”——一个能快速高效适应新任务的理想位置。

但它存在两个关键问题:

• 计算代价高: 每个任务都需要多次梯度更新，对于大型模型或数据集来说极其昂贵。
• 不稳定性: 来自差异较大的任务的梯度求和可能导致冲突的更新，模型被拉向不同方向，影响收敛与稳定。

AMFS 直接针对这些问题，为两个循环分别引入了增强机制。

AMFS 框架: 重新定义速度与稳定性

函数空间中的自适应元学习 (AMFS) 框架结合了两项创新:

1. I-AMFS (内循环 AMFS) : 用核方法的闭式快速解替代了 MAML 内循环的迭代梯度更新。

2. O-AMFS (外循环 AMFS) : 根据任务梯度间的相似性对它们进行加权，稳定跨任务的更新。

它们共同构成一个高效且具坚实理论基础的元学习系统。

I-AMFS: 函数空间中更快的内循环

AMFS 最根本的变革在于学习发生的空间。I-AMFS 不再在参数空间中迭代更新权重，而是在函数空间中直接寻求每个任务的最优函数。

这通过径向基函数 (RBF) 核实现——一种著名的相似性度量，用于衡量两个数据点之间的距离。

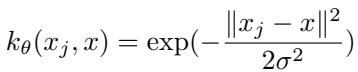
“图: RBF 核通过衡量输入空间中两个数据点的相似程度来捕捉非线性关系。”

利用该核，I-AMFS 将任务适应表述为一个可用闭式求解的优化问题——无需迭代的梯度步骤 。

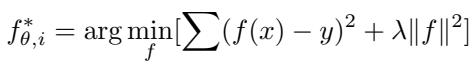
“图: I-AMFS 在最小化训练误差的同时，利用正则化防止函数过度复杂。”

根据表示定理 (Representer Theorem) , 最优函数可以被优雅地表示为:

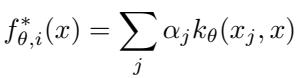
“图: 适应后的函数是核相似度的加权和，实现了快速、直接的计算。”

关键系数 (α) 可直接计算得出:

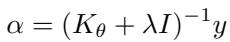
“图: I-AMFS 一次性计算出适应权重，取代了 MAML 的多步梯度更新。”

因此，内循环从多次梯度步骤简化为一次矩阵运算——显著提升了速度。

为保证稳定性与泛化，I-AMFS 引入了含额外正则项的精炼目标函数:

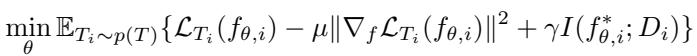
“图: 复合目标提升了适应的平滑性与信息平衡。”

关键正则化组件:

• 梯度范数正则化 (\(\mu ||∇_f L_{T_i}||^2\)) 鼓励更平滑的函数适应，防止过拟合并促进泛化。

• 信息论正则化 (\(\gamma I(f^*; D)\)) 限制函数对训练数据的记忆量，确保跨任务更广泛的学习。

核参数本身也在训练中不断更新，使算法具备更强的适应能力:

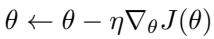
“图: 核参数通过元梯度进行更新，实现了自适应的相似性度量。”

简而言之, I-AMFS 将整个内循环压缩为单一高效步骤 , 同时获得速度与稳定性的双重优势。它用函数空间中的直接优化取代了参数空间的迭代调整——是一项概念与计算的重大飞跃。

O-AMFS: 协调外循环

接下来，AMFS 改进了外循环。MAML 中简单的梯度聚合在任务梯度冲突时容易失效。 O-AMFS 通过依据任务梯度间的相似性对其权重进行调整来解决这一问题，从而在多任务学习中实现协调。

在标准 MAML 中，元更新规则为:

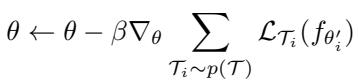
“图: 传统 MAML 在任务梯度聚合时未考虑方向或相互关系。”

O-AMFS 修改为根据余弦相似度——即更新方向是否一致——来加权各任务梯度。

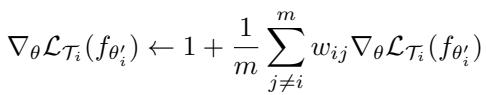
“图: 方向一致的梯度被增强，冲突的梯度被削弱。”

相似性度量 \(w_{ij}\) 计算方式如下:

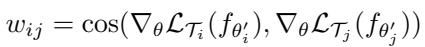
“图: 余弦相似度确保方向一致时更新被强化。”

这确保了方向一致的任务更新相互促进，而偏离方向的任务影响被减弱。

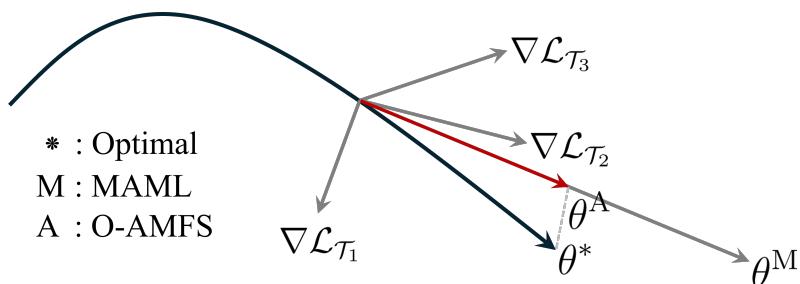
“图1: O-AMFS 保持元更新更接近最优路径 (θ*)，避免冲突梯度方向。”

因此，O-AMFS 形成了更协调的学习轨迹——维持稳定性，提升收敛性，使元学习器更能适应多样任务分布。

实验与结果: 验证 AMFS

研究人员在多个流行的小样本学习基准( Omniglot、Mini-ImageNet、CUB、FC-100 )上验证了 AMFS，并与 MAML 进行了直接对比。

小样本分类准确率

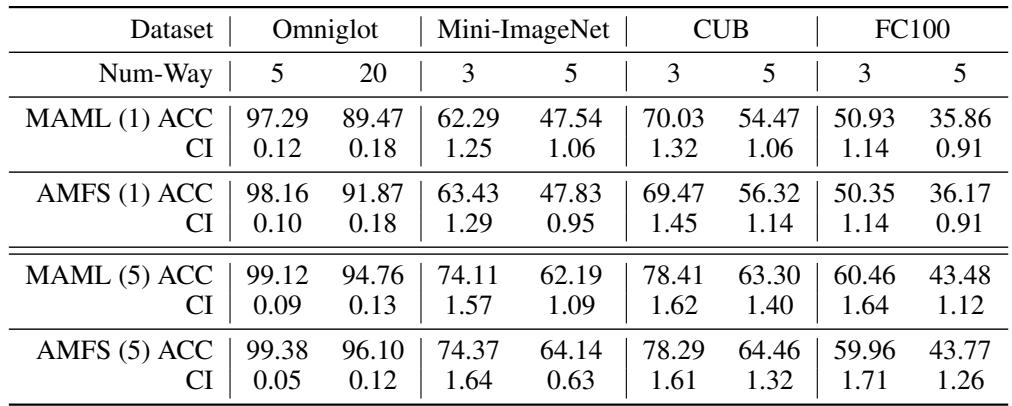
“表1: 在所有数据集和任务难度下，AMFS 的性能均优于或持平于 MAML，验证了其高效与稳定。”

跨所有设置，AMFS 均展示了稳定的性能提升，同时显著降低了计算成本——证明了其优化更高效。

速度的需求: 快速收敛

AMFS 的一大优势是内循环的高效性。作者比较了 MAML 的准确率随梯度步数变化与固定单步 I-AMFS 的表现。

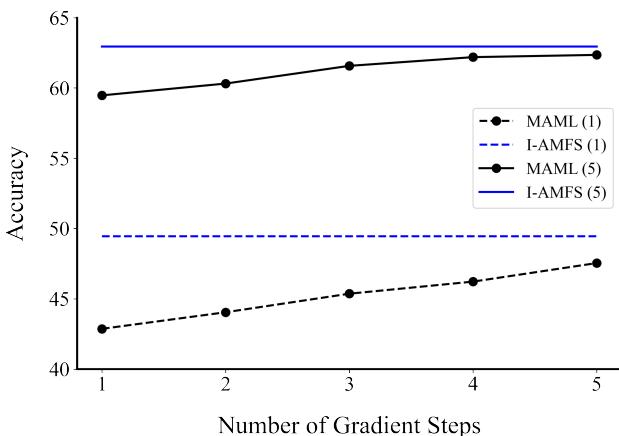
“图2: I-AMFS 仅用一次计算就达到接近最优的准确率，而 MAML 需要多步梯度更新。”

结果显示，I-AMFS 在单次、非迭代的计算中就能实现与五步 MAML 相近的准确率。这意味着更快的训练，以及推理阶段即可即时任务适应。

跨域泛化能力

元学习的最终目标是对未见任务或领域具有强泛化。作者在两种情景下测试了 AMFS:

1. 从通用到特定 (G → S): 在 Mini-ImageNet 上训练，在 CUB (鸟类图像) 上测试。
2. 从特定到通用 (S → G): 在 CUB 上训练，在 Mini-ImageNet 上测试。

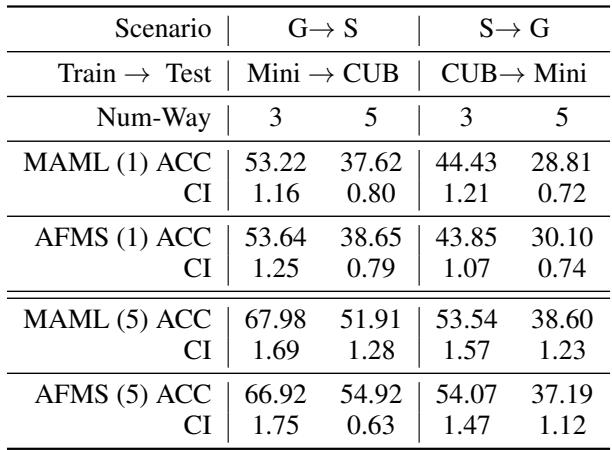
“表2: AMFS 在领域变化下仍保持高准确率，显示其更强的分布外泛化能力。”

即使面对显著分布转移，AMFS 也保持了稳定性能，验证了其在鲁棒领域自适应中的潜力。

对一阶近似的鲁棒性

专注速度的 MAML 变体如**一阶 MAML (FO-MAML)**会省略二阶导数以节省计算，但牺牲了准确性。研究者测试了 AMFS 在该简化条件下的表现。

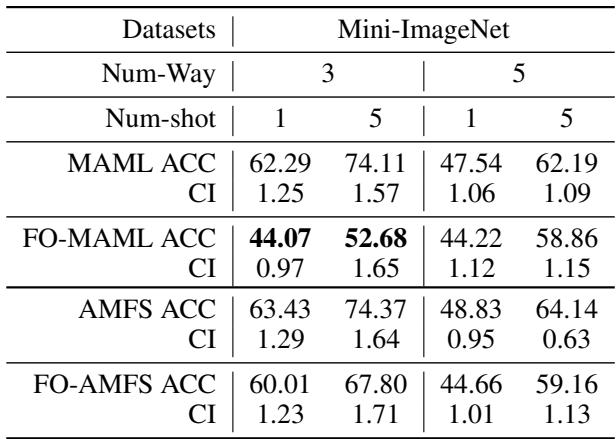
“表4: 得益于梯度加权机制，AMFS 即使在一阶简化下也能保持优异性能。”

即使不使用二阶梯度，AMFS 仍稳定准确，展现了其对近似或噪声优化的内在鲁棒性。

结论: 迈向实用的元学习

论文《Fast Adaptation with Kernel and Gradient Based Meta Learning》为模型无关元学习提供了新的视角。其两大组件——I-AMFS 与 O-AMFS——共同解决了 MAML 的两大核心难题:

• 速度与效率 (I-AMFS) : 任务适应现在是一种一次性的核方法操作，消除了昂贵的梯度迭代。

• 稳定性与协调 (O-AMFS) : 加权梯度聚合平滑了任务间的不一致性，使元更新更趋一致。

这两项增强让 AMFS 不仅更快，更具理论优雅性，也更具实用潜力。

随着深度学习模型的规模和复杂度持续增长，敏捷高效的学习范式变得愈发重要。AMFS 让我们更接近元学习的愿景——创造能快速学会学习的 AI 系统，只需少量数据却具备强适应力。

这项工作不仅是技术创新，更是向机器学习领域中“智能效率”理念迈出的哲学性一步。