两全其美：混合机器学习拍卖如何解决效率与认知负担的权衡

有效分配资源是经济学中的基本问题之一。当资源很简单时 (比如公司的股份) ，标准市场运作良好。但是，当物品各不相同但其价值相互关联时，会发生什么？

试想一下政府向电信公司拍卖频谱许可证的情况。纽约市的许可证很有价值，费城的许可证也很有价值。但对于电信提供商来说，拥有两者的价值可能远高于各部分之和，因为这允许他们建立一个连续的网络。相反，同一城市中的两个不同频率可能是替代品。

这就是组合拍卖 (Combinatorial Auctions, CAs) 的领域。挑战在于？可能的组合数量随着物品数量呈指数级增长。如果有 100 件物品，就有 \(2^{100}\) 种可能的组合——对于任何竞标者来说，要列出所有价值都太多了。

为了解决这个问题，研究人员转向了迭代组合拍卖 (Iterative Combinatorial Auctions, ICAs) , 即拍卖师和竞标者进行多轮互动。最近，机器学习 (ML) 加入了这场争夺，使这些拍卖更加智能化。然而，两种方法之间存在巨大的分歧: 询问价格 (对人类来说更容易，但效率较低) 与询问价值 (效率高，但认知上令人疲惫) 。

在这篇文章中，我们将探讨一个新的框架: 机器学习驱动的混合组合拍卖 (MLHCA) 。 这种机制统一了这两种范式，利用机器学习融合了“价格”和“价值”查询。它在实现最先进效率的同时，也尊重了人类竞标者的认知极限。

核心张力: 需求与价值

在理解解决方案之前，我们必须了解拍卖师用来从竞标者那里提取信息的具体工具。

1. 需求查询 (The Demand Query, DQ)

这是标准的市场互动。拍卖师为每件物品设定价格标签。竞标者看着价格说: “在这个价格下，我想要这个组合。”

在数学上，竞标者 \(i\) 看到价格向量 \(p\)，并选择使其剩余 (价值减去成本) 最大化的组合 \(x\):

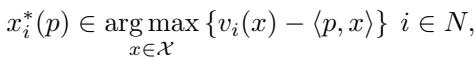
• 优点: 这很自然。这就是我们在超市购物的方式。它降低了认知负担，因为竞标者只需针对当前价格解决最大化问题。
• 缺点: 它提供的仅仅是“低分辨率”信息。如果你花 1 美元买了一个苹果，拍卖师知道你对苹果的估值至少是 1 美元，但不知道你是估值 1.01 美元还是 100 美元。

2. 价值查询 (The Value Query, VQ)

在这里，拍卖师展示一个特定的组合 \(x\) 并问道: “这个组合对你来说到底值多少钱？”

• 优点: 高精度。它为拍卖师提供了估值函数的精确数据点。
• 缺点: 认知过载。试想一下在没有任何价格背景的情况下被问到: “你对包含频谱 A、频谱 C 和频谱 F 的组合的准确美元估值是多少？” 对于人类来说，要在真空中估算随机组合的绝对价值极其困难。

现状

实际拍卖 (如著名的组合时钟拍卖或 CCA) 使用需求查询，因为它们很实用。最近的学术工作 (如 BOCA )使用由机器学习驱动的价值查询，因为它们在理论上是高效的，但在现实世界中却难以实施，因为竞标者无法有效地回答随机价值问题。

学习问题

在机器学习驱动的拍卖中，目标是训练一个模型 (具体来说是神经网络) 来学习每个竞标者的私人估值函数 \(v_i(x)\)。拍卖师使用这个模型来预测分配哪些组合是有效的。

MLHCA 背后的研究人员发现了仅依赖一种查询类型的关键缺陷。

价值查询 (VQs) 的缺陷: 如果以 VQ 开始拍卖，本质上就是在大海捞针 (盲目射击) 。在高维空间中，随机询问到一个“好”组合 (竞标者实际想要的组合) 的概率接近于零。在随机 VQ 上训练的 ML 模型无法捕捉到空间的“高价值”区域。

需求查询 (DQs) 的缺陷: DQ 擅长寻找“高价值”区域，因为竞标者自然会选择好的组合。然而，它们无法确定确切的价值。正如论文所证明的那样，即使有无限次查询，基于 DQ 的拍卖也无法保证完全有效率。

为了弥补这一差距，研究人员提出了混合查询学习 。 他们用需求查询初始化拍卖以找到组合空间的相关部分，然后切换到价值查询以确定确切数字。

可视化学习收益

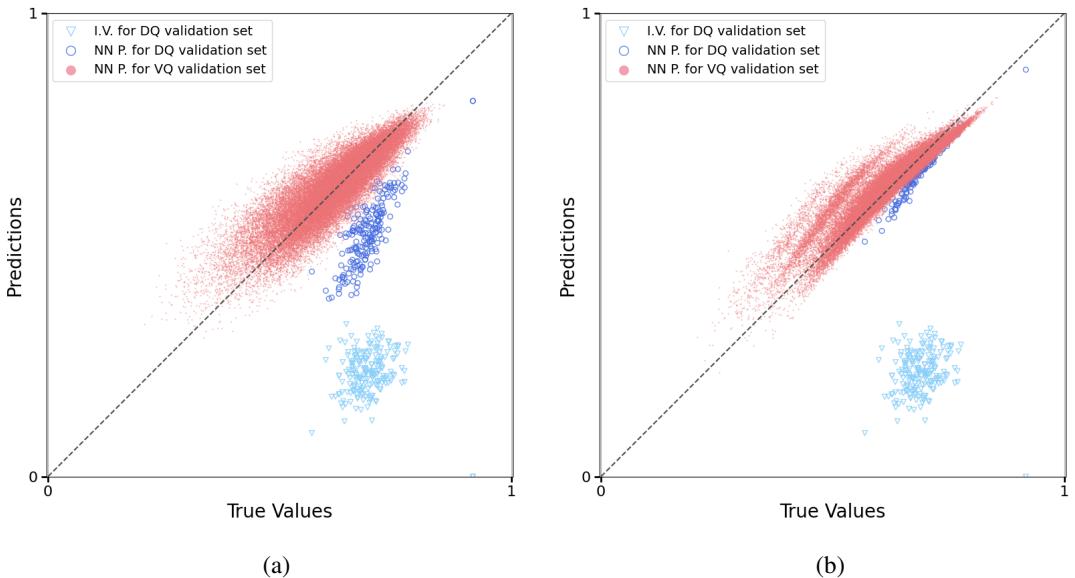
下图展示了预测竞标者价值的神经网络的性能。

• 图 (a) 显示了仅在需求查询上训练的模型。注意那些蓝点 (针对竞标者实际想要的组合的预测) 。它们形成了一条与真实值平行但有偏移的线。模型学会了偏好的结构 (相对价值) ，但没有学会量级 (绝对价值) 。
• 图 (b) 显示了混合模型。通过添加价值查询，模型“对齐”到了对角线上。它既知道结构也知道绝对数字。

机制: MLHCA

MLHCA 被设计为一个分阶段的过程。它从粗略探索 (价格) 过渡到精确利用 (价值) 。

以下是拍卖的高级工作流程:

第一阶段: 组合时钟 (第 3-6 行)

拍卖像标准的组合时钟拍卖 (CCA) 一样开始。价格从低位起步，并随着需求过剩的物品而上涨。这作为一个“热身”过程，生成简单的初始数据点 (DQ) ，竞标者在此揭示他们的大致兴趣。

第二阶段: 机器学习驱动的需求查询 (第 7-12 行)

一旦初始阶段完成，ML 引擎启动。拍卖师在收集到的数据上训练一个单调价值神经网络 (mMVNN) 。

拍卖师不仅仅是按固定百分比提高价格，而是使用 ML 模型生成“智能价格”。他们解决一个优化问题，根据模型对竞标者的了解，找到最有可能出清市场 (匹配供需) 的价格向量。

第三阶段: “桥梁出价” (第 17-18 行)

这是一个理论上至关重要的创新。从需求查询 (价格) 到价值查询 (直接提问) 的过渡实际上可能很危险。研究人员证明，简单地切换查询类型可能会导致效率 (后悔值) 突然下降。

为了防止这种情况，他们引入了桥梁出价 (Bridge Bid) 。 在开始价值查询阶段之前，拍卖师会问一个具体的问题:

“你对目前 (在推断分配中) 持有的组合的确切估值是多少？”

这个单一数据点锚定了 ML 模型，确保拍卖效率只能上升，不会下降。

第四阶段: 机器学习驱动的价值查询 (第 19-35 行)

既然 ML 模型已经有了估值景观的良好“草图” (来自 DQ) 并已正确锚定 (来自桥梁出价) ，它就开始提出具体的价值查询。 它使用 ML 模型来解决赢家确定问题 (WDP) : 找到根据模型使社会福利最大化的分配，然后查询该分配中涉及的具体组合。

幕后的数学原理

“推断价值”是拍卖师决策的核心。即使竞标者没有说明他们对某个组合的确切价值，他们之前的回答也设定了一个下限。

在数学上，如果竞标者看到价格 \(p\) 并选择了组合 \(x\)，我们知道他们对 \(x\) 的利润 (概念上) 高于任何其他组合 \(y\)。这允许拍卖师构建一个下限函数 \(\tilde{v}_i\):

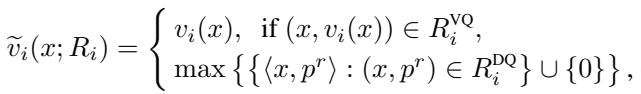
第一种情况很简单: 如果我们询问了价值查询，我们就知道价值 \(v_i(x)\)。 第二种情况处理需求查询: 推断价值是与竞标者之前的价格响应一致的最大下限。

拍卖师总是根据这些推断价值计算赢家:

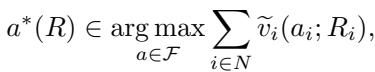
实验结果

这种混合方法真的有效吗？研究人员在频谱拍卖测试套件 (SATS) 上测试了 MLHCA，这是模拟大规模频谱拍卖的黄金标准。

他们将 MLHCA 与以下方法进行了比较:

1. CCA: 现实世界中使用的标准非 ML 拍卖。
2. ML-CCA: 仅使用价格 (DQ) 的 ML 拍卖。
3. BOCA: 仅使用价值 (VQ) 的最先进 ML 拍卖。

效率和收敛性

下图绘制了“效率损失” (越低越好) 与出价/查询数量的关系。

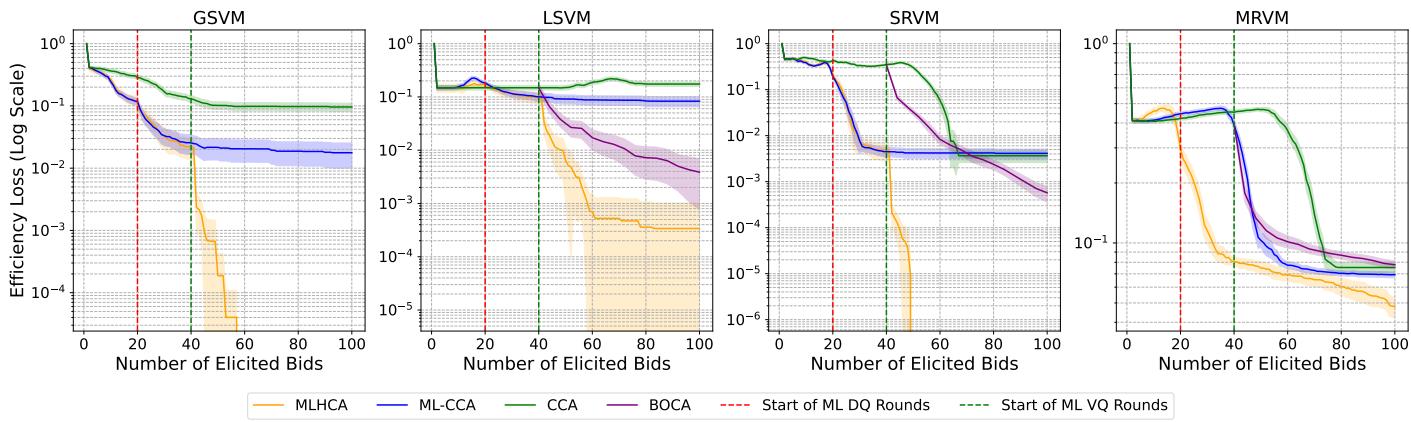
• 早期阶段 (0-40 次出价) : MLHCA (橙色) 与 ML-CCA (蓝色) 一致。它使用价格，这在早期非常有效。注意 BOCA (紫色，使用随机 VQ) 最初很难提高效率——它在“高维空间”中迷失了方向。
• 后期阶段 (40+ 次出价) : 在第 40 次出价时，MLHCA 切换到价值查询 (由红色虚线标记) 。效率损失立即骤降。它优于 ML-CCA (后者陷入停滞) 并保持领先于 BOCA。

在最紧密模拟现实 4G 频谱拍卖的 MRVM 领域 (多区域价值模型) 中，与之前的最先进技术相比，MLHCA 将效率损失减少了 10 倍。以美元计算，对于数十亿美元的频谱拍卖，这可能代表着数亿美元的社会福利增益。

桥梁出价的重要性

理论警告说，切换查询类型可能会损害效率。实验证实了该解决方案。下图显示了有 (橙色) 和没有 (蓝色) 桥梁出价的 MLHCA。

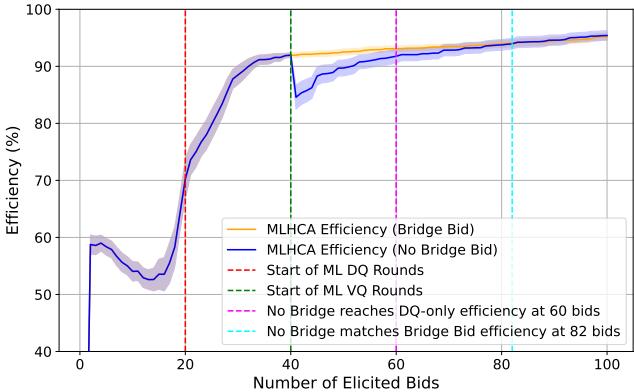
如果没有桥梁出价，效率实际上会在价值查询开始时 (大约第 40 次出价) 下降。仅仅为了恢复到之前的水平大约需要 20 次额外的查询。有了桥梁出价，过渡是平滑且单调的。

结论

MLHCA 代表了机制设计中机器学习的成熟。它不再试图强行采用纯粹的“ML 原生”方法 (如仅做价值查询) ，而是尊重拍卖的经济和人类现实:

1. 从价格 (DQ) 开始: 它们认知上很简单，并且非常适合对竞标者的大致需求进行“全局探索”。
2. 以价值 (VQ) 结束: 它们提供了最优分配所需的数学精度。
3. 使用 ML 作为粘合剂: 神经网络将这两个不同的数据流整合到一个单一的、连贯的竞标者偏好模型中。

通过策略性地结合这些查询类型，MLHCA 建立了一个新的基准。它创造的拍卖不仅在数学上更有效率，而且收敛更快，也更容易被人类参与者信任和使用。