在算法博弈论和大规模物流领域，一个根本性的问题长期存在: 当你需要从多人手中购买服务，而这些人可能会谎报价格时，你该如何确保获得最高的“性价比”？

想象一下，一个政府机构试图从不同的供应商那里采购医疗物资，或者一个众包平台正在雇佣自由职业者来标注数据。买方 (拍卖人) 希望选择一组卖方，以最大化服务的总价值减去支付的成本。这就是所谓的采购拍卖 (Procurement Auction) 。

然而，这其中有一个陷阱。这些服务的价值往往表现出边际收益递减的特性——即次模性 (Submodularity) 。 例如，雇佣两名翻译很棒，但雇佣一百名翻译增加的价值可能并不比雇佣五十名多多少。此外，卖方是策略性的；他们会通过报出高于实际成本的价格来最大化自己的利润。

在这篇深度文章中，我们将探讨一篇旨在弥合复杂优化算法与经济机制设计之间鸿沟的研究论文。我们将通过该论文了解研究人员如何开发出一个框架，将最先进的近似算法转化为诚实、高效的拍卖机制。

核心问题: 福利 vs. 成本

这项工作的目标不同于标准的收入最大化。这里的目标是在采购场景中最大化社会福利 (Social Welfare) 。 具体来说，拍卖人希望选择一个卖方子集 \(S\)，以最大化获得的价值 \(f(S)\) 与产生的成本 \(\sum c_i\) 之间的差额。

挑战在于，即使是在已知成本的情况下，找到最优集合 \(S\) 在计算上也是困难的 (NP-hard) ，尤其是当 \(f(S)\) 是一个次模函数时。更糟糕的是，拍卖人并不知道卖方的真实成本——只知道他们提交的报价。

研究人员旨在设计一种满足三个关键属性的机制:

  1. 激励相容 (Incentive Compatibility, IC) : 如实报告成本符合卖方的最大利益。
  2. 个体理性 (Individual Rationality, IR) : 卖方参与拍卖绝不会亏本 (他们获得的支付能覆盖成本) 。
  3. 拍卖人非负盈余 (Non-negative Auctioneer Surplus, NAS) : 拍卖人获得的价值至少等于支付的总金额。

论文为这个问题提供了一个双准则 (bi-criteria) 近似保证，表示为:

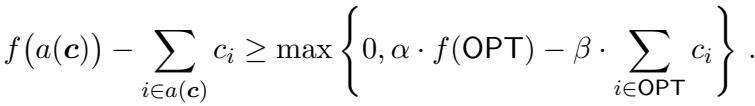
双准则近似保证公式。

在这里，\(\alpha\) 和 \(\beta\) 代表近似中的权衡。目标是让 \(\alpha\) 接近 1 且 \(\beta\) 接近 1。

算法引擎: 次模优化

在设计拍卖之前，我们需要一个假设已知成本就能解决优化问题的算法。论文重新审视了几种贪心算法，并为它们提供了改进的分析。

所有这些算法都遵循类似的“元算法 (meta-algorithm) ”结构: 它们迭代地构建解决方案集 \(S\)。在每一轮中，它们为每一个尚未在集合中的项目 \(i\) 计算一个得分 \(G(i, S, c)\)。如果最高得分为正，则将该项目加入集合。

让我们来看看论文中分析的具体评分函数。

1. 边际贪心 (Greedy-Margin)

最直观的方法是边际贪心算法。它简单地考察边际增益——即一个项目增加的价值减去其成本。

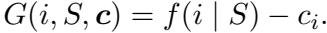
边际贪心评分函数。

虽然简单，但该算法并不能始终提供最佳的最坏情况保证，因为它没有考虑回报的“率”。

2. 比率贪心 (Greedy-Rate) 和 ROI 贪心

为了解决简单边际方法的不足，我们可以查看增益与成本的比率 (投资回报率或 ROI) 。 比率贪心算法优先考虑效率。

比率贪心评分函数。

另外, ROI 贪心算法使用了略有不同的分母，但实现了类似的排名逻辑。

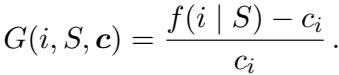
ROI 贪心评分函数。

3. 扭曲贪心算法 (Distorted Greedy Algorithm)

重头戏是扭曲贪心算法。这种方法对边际贡献引入了与时间相关的扭曲。随着算法的进行 (当 \(k\) 向 \(n\) 增加时) ，放置在边际价值上的权重会发生变化。

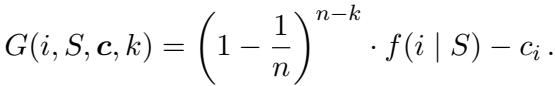
扭曲贪心评分函数。

项 \((1 - 1/n)^{n-k}\) 起到了阻尼器的作用。该算法的独特之处在于，即使边际增益减去成本为负，它也不一定会停止；评分函数的结构使其能够有效地在非正次模最大化场景中导航。

研究人员还分析了该算法的随机 (Stochastic) 版本以加快计算速度，该版本在每一步随机抽样卖方而不是评估所有人。

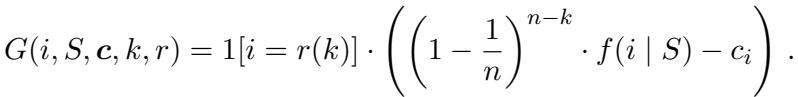
随机扭曲贪心评分函数。

4. 成本缩放贪心 (Cost-Scaled Greedy)

最后是成本缩放贪心算法。这对在线设置 (卖方逐一到达) 特别有用。它通过乘以一个因子 (在本例中为 2) 来更积极地惩罚高成本。

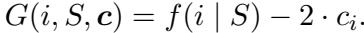
成本缩放贪心评分函数。

改进的理论保证

论文的理论贡献之一是对扭曲贪心算法进行了更严格的分析。作者证明该算法同时对所有 \(\beta \in [0, 1]\) 满足 \((1 - e^{-\beta}, \beta)\) 的保证。这将该算法置于此类问题理论上可能的帕累托前沿。

数学上的重头戏涉及定义势函数 \(\Phi\) 和 \(\Psi\) 来跟踪算法的价值积累与成本积累。

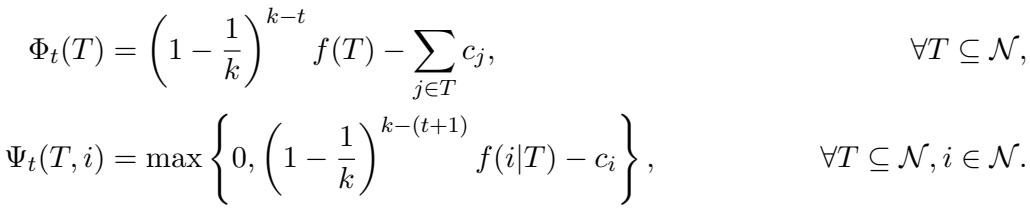
扭曲贪心分析的势函数定义。

通过分析每一步势函数的差异，作者推导出了改进的界限。

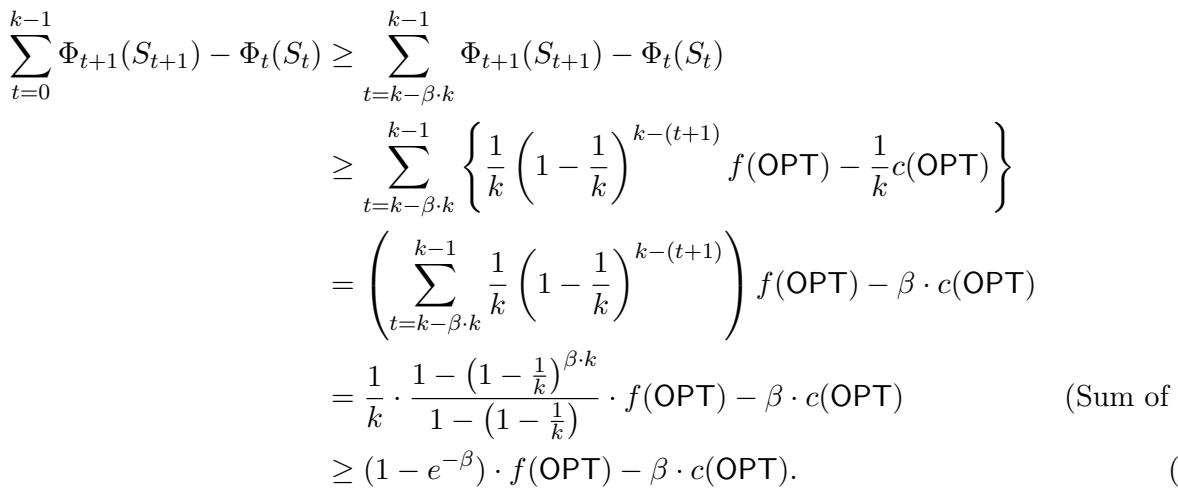
势函数差异的分析。

这个不等式表明，算法积累价值的速率保证了最终福利接近最优解。

从算法到机制

这项工作最大的实际贡献是一个框架，它将上述算法转化为诚实机制 (Truthful Mechanisms) 。

在机制设计中，VCG (Vickrey-Clarke-Groves) 机制是确保诚实性的标准解决方案。它根据一个参与者对其他人施加的“外部性”来计算支付。

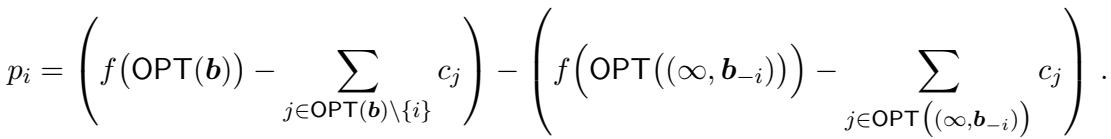
VCG 支付公式。

然而，VCG 在此背景下有一个致命缺陷: 它需要精确解决优化问题以保持诚实性。由于我们的问题是 NP-hard 的，我们无法有效地运行 VCG。

新框架

作者提出了一种方法，将上述贪心算法转化为既计算高效又诚实的机制。

直觉依赖于临界支付 (Critical Payment) 概念。对于一个诚实的机制，分配规则 (谁赢) 必须是单调的 (出价更低永远不会损害获胜机会) ，且支付必须是“阈值”出价。如果卖方的出价高于这个阈值，他们就会输；如果低于这个阈值，他们仍然会赢。

该框架的工作原理如下:

  1. 分配: 使用提交的出价作为成本运行选定的元算法 (例如，扭曲贪心) 。
  2. 支付: 对于每个获胜的卖方 \(i\)，假设卖方 \(i\) 出价 \(\infty\) (本质上是将其移除) 重新运行算法。然后，找到卖方 \(i\) 可以提交的最高出价 \(b_i\)，使得其仍然能被算法选中。

论文证明，只要评分函数 \(G\) 是关于出价 \(b_i\) 的非递增函数 (所有贪心算法都符合这一点) ，这种构造就能产生一个满足 IC 和 IR 的机制。

确保拍卖人非负盈余 (NAS)

至关重要的是，机制必须确保拍卖人不会破产。支付给卖方的总金额不得超过产生的价值 \(f(S)\)。

对此的证明依赖于这样一个属性: 只有当卖方的得分为正时才会被选中。这意味着他们的出价相对于其边际贡献有一个界限。

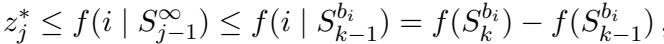
NAS 证明的临界支付界限。

通过对所有赢家求和这些界限，作者表明总支付受限于边际贡献的伸缩求和 (telescoping sum) ，该总和等于总价值。

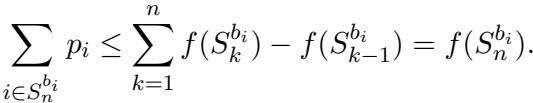
拍卖人非负盈余的求和证明。

这证实了拍卖人是安全的: 盈余将始终为非负。

在线和降价拍卖

该框架不仅限于静态的密封投标拍卖。

在线机制

在许多零工经济应用中，工人 (卖方) 是按顺序到达的。拍卖人必须立即决定是否雇佣他们。这被建模为在线机制 (Online Mechanism) 。

作者表明，这些算法可以转化为标价机制 (Posted-Price Mechanisms) 。 当一个卖方到达时，算法根据先前卖方的历史计算一个“一口价 (take-it-or-leave-it) ”。

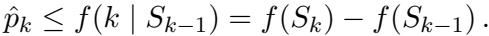
在线机制的阈值价格条件。

如果卖方的成本低于此阈值，他们就会接受工作。这保留了底层在线算法 (如成本缩放贪心) 的近似保证。

降价拍卖

降价拍卖 (Descending Auction) (或称荷兰式拍卖) 的工作原理是从高价开始，不断降低价格直到有卖方同意接受。这些拍卖很受欢迎，因为它们是“显然策略防范 (obviously strategy-proof) ”的——最佳策略显然是留在拍卖中直到价格达到你的成本。

论文揭示了一个关于对抗性设置 (价格降低顺序是最坏情况) 下降价拍卖的惊人结果。他们表明，使用“完美”需求预言机 (即精确解决优化的预言机) 的降价拍卖实际上可能表现得任意差。

然而，如果拍卖人使用基于成本缩放贪心算法的需求预言机，拍卖将保持 \((1/2, 1)\) 的近似保证。这是一个有趣的例子，表明在动态拍卖设置中，近似算法比精确算法更稳健。

实验结果

为了验证这些理论框架，研究人员使用 SNAP “Wiki-Vote” 数据集进行了实验，模拟了一个覆盖问题 (一种经典的次模函数) 。他们比较了不同机制的运行时间和福利。

运行时间

正如预期的那样，计算精确的最优福利 (和 VCG 支付) 是指数级缓慢的。基于贪心的方法要快几个数量级。

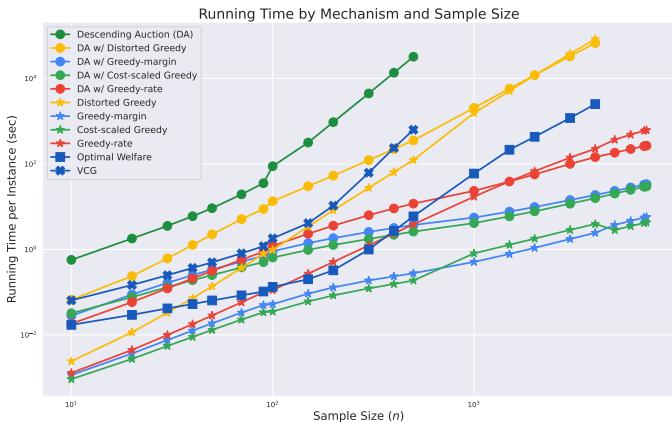
不同机制的运行时间比较。

在图 1 中，注意 VCG 和“降价拍卖 (Descending Auction) ” (使用精确预言机) 的线条急剧上升，而贪心变体 (边际贪心、成本缩放) 保持低位。扭曲贪心比其他贪心方法稍慢，但仍是多项式时间的。

福利表现

使用这些近似方法会损失多少价值？实验绘制了福利与“活跃代理人比例 (Fraction of Active Agents) ” (衡量市场竞争程度的指标) 的关系图。

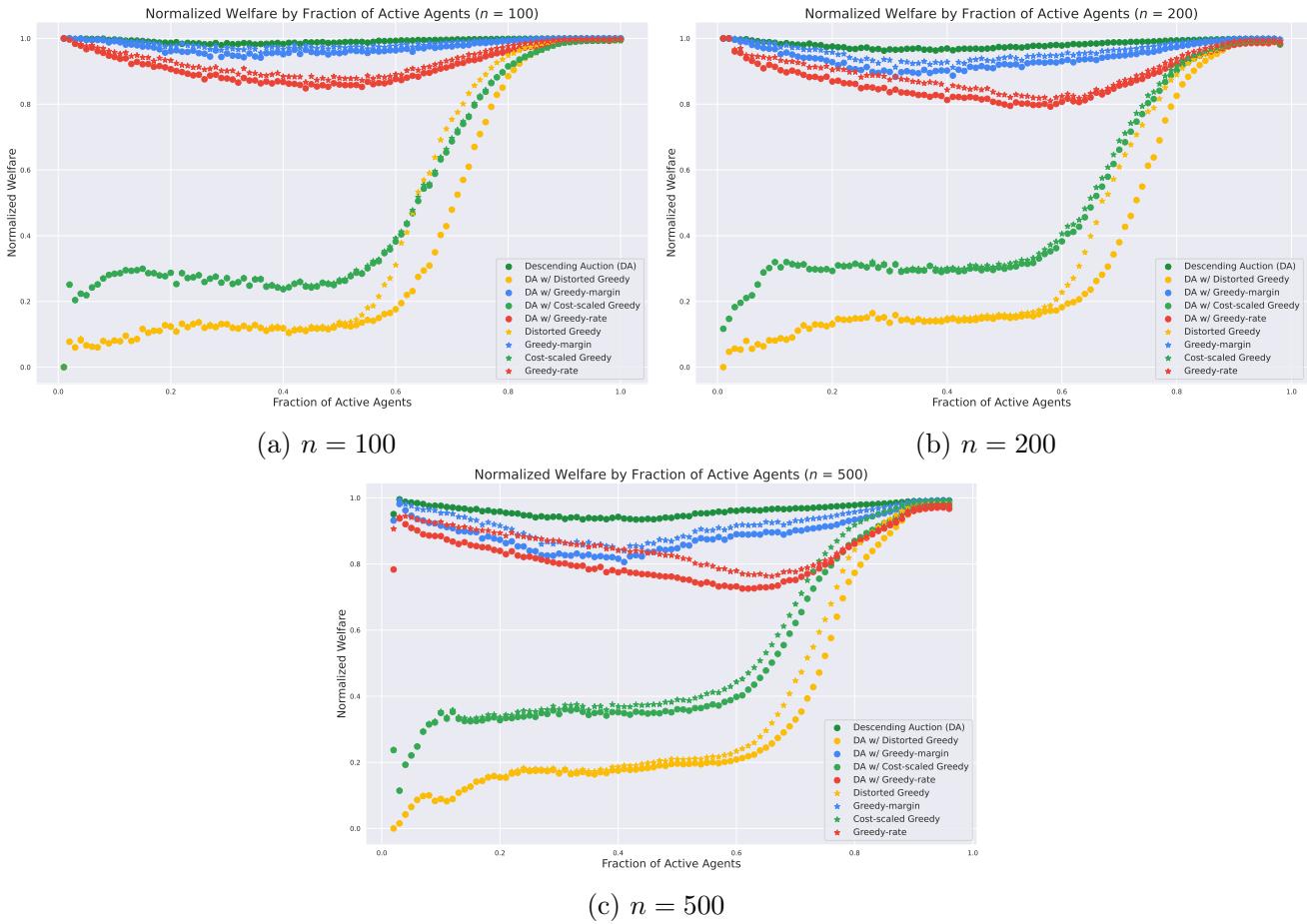
n=100, 200, 500 时的福利比较。

在图 2 中，我们看到了归一化福利。关键结论是性能的层次结构:

  1. 边际贪心 (Greedy-margin) 通常在近似算法中表现最好。
  2. 比率贪心 (Greedy-rate) 和成本缩放 (Cost-scaled) 紧随其后。
  3. 扭曲贪心 (Distorted Greedy) 虽然理论上稳健，但在平均情况下的实证福利有时略微落后于激进的边际贪心。

表 1 总结了在此框架中实例化的算法的理论保证。

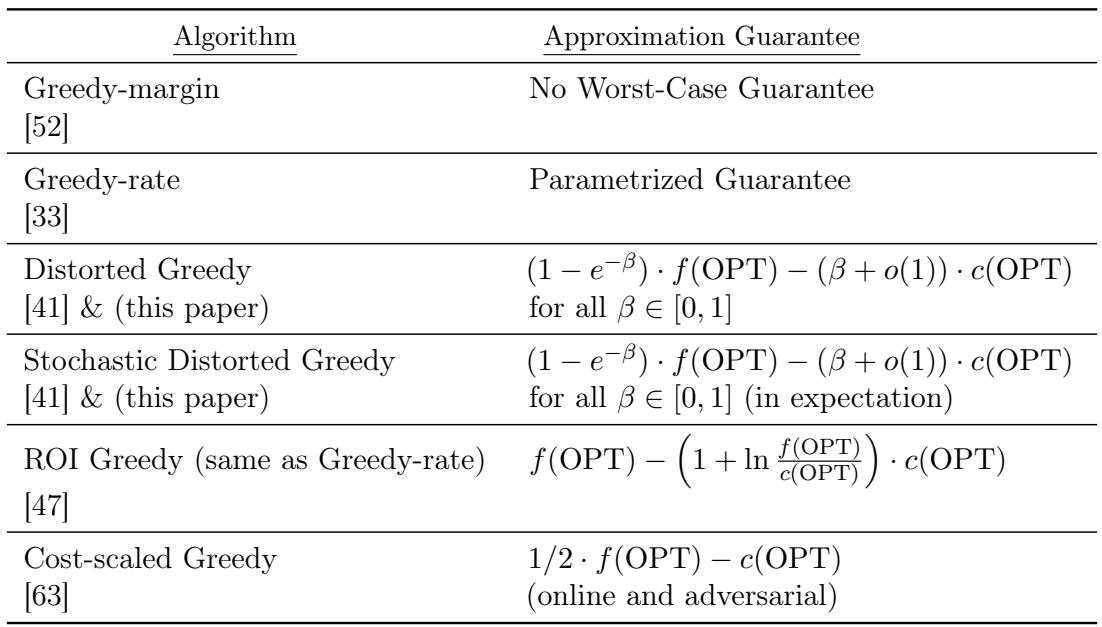
算法实例化和保证表。

值得注意的是，虽然边际贪心在实践中表现良好 (图 2) ，但它没有最坏情况下的理论保证 (表 1) 。相反，扭曲贪心拥有最佳的理论保证，但在实践中更为保守。

结论

这项研究为现代采购提供了一个全面的工具包。通过利用次模函数的特定数学属性，作者架起了两个世界之间的桥梁:

  1. 优化: 高效解决复杂的选择问题。
  2. 经济学: 处理策略性行为并确保诚实报价。

提出的框架允许从业者采用“现成的”次模优化算法，并将其包装在保证诚实性和预算安全的支付方案中。无论是用于离线密封投标拍卖还是实时在线市场，这项工作都为更高效、更公平的采购系统提供了一条严谨的路径。

对于构建下一代物流或众包平台的学生和工程师来说，教训很清楚: 你不必在计算速度和经济稳健性之间做出选择。通过正确的机制设计，你可以兼得。