引言

在决策领域，数据为王。但数据也是杂乱、有限且充满噪声的。无论你是管理股票投资组合、为商店备货，还是训练机器学习模型，你很少知道生成数据的真实机制。相反，你必须对其进行估计。

标准方法是收集数据，拟合一个概率分布 (你的模型) ，并根据该模型做出最小化预期风险的决策。在贝叶斯框架中，你会更进一步: 将数据与先验信念结合，得到后验分布，从而更好地感知参数的不确定性。

但这里有个陷阱: 如果你估计的模型——即使是贝叶斯模型——稍有偏差怎么办？

当你针对单个估计模型 (或它们的平均值) 进行过度激进的优化时，你往往会成为优化者诅咒 (Optimizer’s Curse) 的受害者。你会根据有限数据的特定偏差完美地调整你的决策，导致面对现实世界时表现崩溃。实际上，你是对你的不确定性进行了“过拟合”。

这篇文章将探讨论文 Decision Making under the Exponential Family: Distributionally Robust Optimisation with Bayesian Ambiguity Sets 中提出的一种令人着迷的解决方案。作者介绍了一种名为 DRO-BAS 的框架。它结合了贝叶斯统计的不确定性量化与分布鲁棒优化 (DRO) 的安全网。结果不仅数学上优雅，而且在计算速度和经验安全性方面都优于现有的替代方案。

背景: 决策者的困境

在深入探讨新方法之前，让我们先为这个故事中的三个主要角色搭建舞台: 标准贝叶斯主义者、鲁棒优化者和“现有”的混合方法。

1. 标准贝叶斯主义者

在标准的贝叶斯风险优化 (BRO) 中，你观察后验分布 (看到数据后你对模型参数的信念) ，并最小化期望损失。

\[ \operatorname* { m i n } _ { x \in \mathcal { X } } \mathbb { E } _ { \theta \sim \Pi ( \theta | \mathcal { D } ) } \left[ \mathbb { E } _ { \xi \sim \mathbb { P } _ { \theta } } [ f _ { x } ( \xi ) ] \right] . \]

Standard Bayesian Risk Objective 虽然这考虑了参数的不确定性，但它假设你的贝叶斯模型是正确的。如果现实世界 (数据生成过程，DGP) 偏离了你的模型族，或者你的先验设定有误，这种方法无法提供保障。

2. 鲁棒优化者 (DRO)

分布鲁棒优化 (DRO) 采取最坏情况的视角。你不针对单一分布进行优化，而是定义一个模糊集 (Ambiguity Set) ——一个包含接近你估计值的分布的“球”。然后，你寻找一个能在这个球内最小化最坏可能风险的决策。如果你能在这个球内的最坏情况下保持安全，那么你在现实世界中也很可能是安全的。

3. 现有的混合方法 (BDRO)

以前试图结合这两种方法的尝试，如贝叶斯 DRO (BDRO) ，试图平均这种鲁棒性。它们会从后验中采样参数，围绕每个参数构建一个小模糊球，计算每个球的最坏情况风险，然后平均这些风险。

\[ ( B D R O ) \underset { x \in \mathcal { X } } { \mathrm { m i n } } \ \mathbb { E } _ { \theta \sim \Pi ( \theta | \mathcal { D } ) } \left[ \operatorname* { s u p } _ { \mathbb { Q } \in \mathcal { B } _ { \epsilon } ( \mathbb { P } _ { \theta } ) } \ \mathbb { E } _ { \xi \sim \mathbb { Q } } [ f _ { x } ( \xi ) ] \right] , \]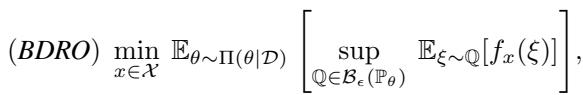

BDRO Formulation

虽然比什么都不做要好，但 BDRO 在计算上非常繁重。这是一个“两阶段”问题: 你必须在一个期望积分内解决一个最大化问题 (寻找最坏风险) 。在实践中，这需要嵌套的采样循环，既慢又低效。此外，它并不严格对应于单个“最坏情况”分布，这使得它更难解释。

解决方案: 贝叶斯模糊集 (DRO-BAS)

研究人员提出了一种更清晰、更严谨的方法: DRO-BAS 。 与其平均许多模型的最坏情况，为什么不定义一个直接包含贝叶斯后验的单一模糊集呢？

他们提出了两种具体的集合构建方式，定义如下:

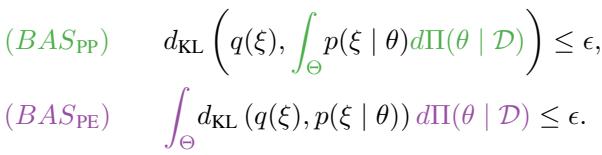
Definitions of BAS-PP and BAS-PE

让我们从视觉和数学角度来分解这些概念。

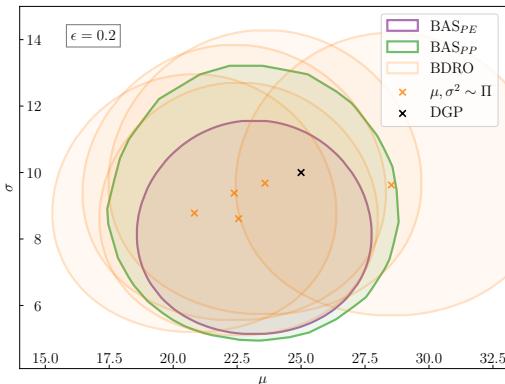
Visualisation of ambiguity sets

如上方的 图 1 所示，这些方法在几何形状上有所不同:

  • BDRO (现有): 围绕单个后验样本 (橙色十字) 的最坏情况风险取期望。
  • BAS-PP (绿色): 一个以后验预测分布为中心的球。
  • BAS-PE (紫色): 一个由到模型族的期望 KL 散度定义的集合。

1. 基于后验预测的 BAS (DRO-BAS\(_{PP}\))

结合贝叶斯推断与 DRO 最直观的方法是关注后验预测分布 (\(\mathbb{P}_n\)) 。这是当你根据后验概率加权平均所有可能的模型时得到的单一分布。

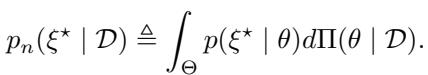
Posterior Predictive Definition

BAS\(_{PP}\) 方法简单地创建了一个以该预测分布为中心的标准 Kullback-Leibler (KL) 散度球:

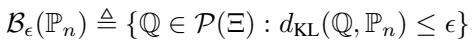
BAS-PP Ambiguity Set

目标是最小化这个球内的最坏情况风险:

DRO-BAS PP Objective

优点: 这是一个纯粹的“最坏情况”方法。它具有强对偶形式，这意味着我们可以将复杂的最小化-最大化问题转化为一个更简单的最小化问题:

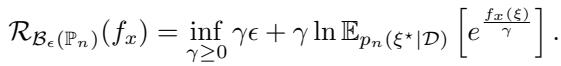
Dual Formulation of BAS-PP

缺点: 后验预测分布通常采取复杂的形式。例如，如果你有一个高斯似然和一个 Gamma 先验，你的预测分布就是一个 Student-t 分布。计算矩生成函数 (MGF)——即上式中的 \(\mathbb{E}[e^{f_x}]\) 项——对于 Student-t 分布通常是不可能的，因为它可能不存在或为无穷大。这迫使我们使用采样 (样本均值近似) 来近似分布，从而重新引入了估计误差。

2. 基于后验期望的 BAS (DRO-BAS\(_{PE}\))

这是论文的主要贡献。 BAS\(_{PE}\) 不是将球心放在预测分布上，而是基于到模型族的期望距离来定义模糊集。

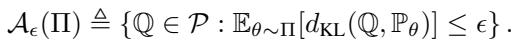
BAS-PE Set Definition

在这里，模糊集 \(\mathcal{A}_\epsilon(\Pi)\) 包含所有满足以下条件的分布 \(\mathbb{Q}\): \(\mathbb{Q}\) 到参数模型 \(\mathbb{P}_\theta\) 的平均 KL 散度 (由后验加权) 很小。

这听起来可能比较抽象，但在处理指数族分布时，它具有一种“神奇”的性质。

指数族分布的优势

指数族包括许多统计学中最常见的分布: 正态 (高斯) 、指数、Gamma、Beta、伯努利和泊松分布。

当似然模型属于指数族且我们使用共轭先验时，数学运算会变得非常简洁。作者证明，对于这些模型，复杂的优化问题会坍缩为一个单阶段随机规划 。

具体来说，如果满足条件 (共轭先验和指数似然) ，我们可以精确计算最坏情况风险，而无需嵌套的采样循环。

BAS\(_{PE}\) 的通用对偶形式为:

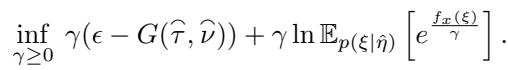
Dual Formulation for BAS-PE

注意项 \(G(\hat{\tau}, \hat{\nu})\)。这是一个基于后验参数推导出的常数。因为我们可以对指数族解析地计算这个值，所以不需要对其进行估计。

一个具体例子: 高斯模型的线性目标

为了看到 BAS\(_{PE}\) 的威力，考虑一个场景: 你的目标函数是线性的 (比如最小化投资组合成本) ，而你的数据是高斯的。

如果你使用 DRO-BAS\(_{PE}\)，优化问题变成了一个闭式方程:

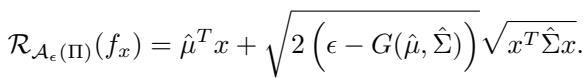
Closed form for Gaussian

其中:

  • \(\hat{\mu}\) 和 \(\hat{\Sigma}\) 是后验均值和协方差。
  • \(G(\dots)\) 是根据你的不确定性计算出的常数。
  • \(x\) 是你的决策变量。

没有积分，没有蒙特卡洛采样，没有循环。你将这个方程输入标准求解器，它会立即给出最优的鲁棒决策。相比 BDRO，这是一个巨大的计算优势。

实验结果

理论很美好，但实际效果如何？作者在两个经典问题上测试了这些方法: 报童问题 (库存管理) 和投资组合优化。

1. 报童问题 (The Newsvendor Problem)

在这个问题中，零售商必须决定储备多少库存 (\(x\)) 以满足不确定的需求 (\(\xi\)) 。库存太多，你会损失持有成本。库存太少，你会损失潜在的销售额。

作者在“样本外” (OOS) 表现上比较了这些方法。他们在小数据集上训练决策，并在未见过的数据上进行测试。他们绘制了成本的均值与方差 。 理想情况下，你希望位于左下角 (低成本，低方差) 。

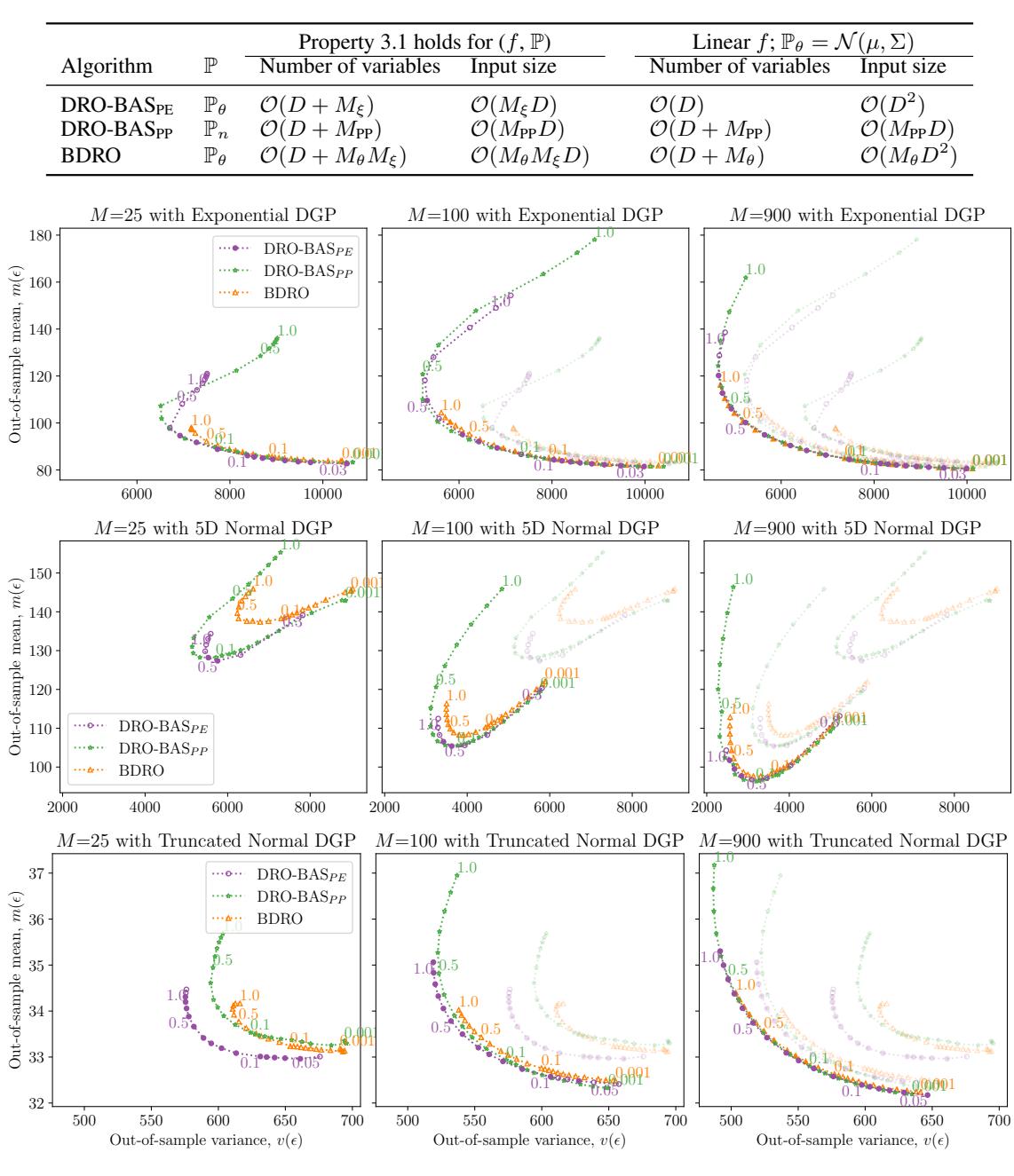
Newsvendor Results

上方的 图 2 展示了不同数据生成过程 (DGP) 下的结果。

  • 紫色点线 (DRO-BAS\(_{PE}\)) 始终构成“帕累托前沿” (最优边界) 。它优于其他方法，在相同回报下提供更低的风险。
  • 橙色线 (BDRO) 需要显著更多的样本 (\(M=900\)) 才能接近 DRO-BAS 用更少资源达到的性能。
  • 注意中间一行 (正态 DGP) : BAS\(_{PE}\) 严格优于 (更低且更靠左) BDRO。

2. 投资组合问题 (The Portfolio Problem)

这里的目标是在资产之间分配财富，以最大化回报 (或最小化负回报) ，同时管理风险。数据是道琼斯指数的真实周回报率。

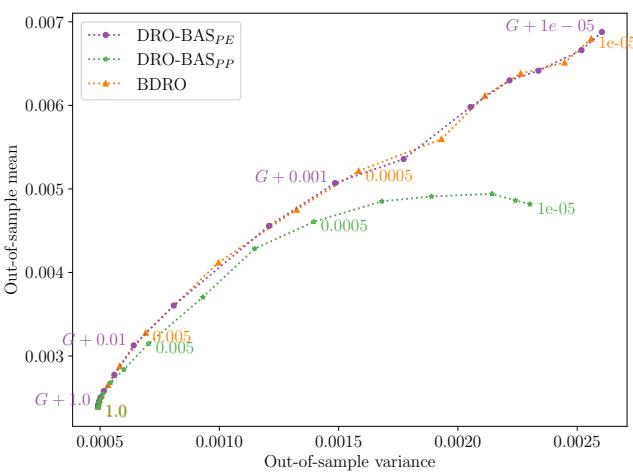
Portfolio Results

在 图 3 中，我们看到了均值-方差权衡。

  • DRO-BAS\(_{PE}\) (紫色) 和 BDRO (橙色) 在鲁棒性方面表现相似。
  • DRO-BAS\(_{PP}\) (绿色) 在这里表现挣扎，可能是因为 Student-t 预测分布迫使使用了降低性能的采样近似。

然而，这里真正的区别在于速度 。

Computation Time Table

表 2 揭示了计算上的差距。

  • DRO-BAS\(_{PE}\) 求解仅需 0.01 秒 。
  • BDRO 需要 4.47 秒 。

这是 400 倍的加速 。 在高频交易或实时物流中，这种差异至关重要。BDRO 之所以慢，是因为它必须从逆 Wishart 分布中采样协方差矩阵并求解一个两阶段问题。DRO-BAS\(_{PE}\) 只需要求解一个单一的解析方程。

结论与要点

论文 “Decision Making under the Exponential Family” 为重新思考我们在优化中如何处理不确定性提供了令人信服的论据。

以下是给学生和从业者的关键要点:

  1. 不要平均最坏情况: 现有的 BDRO 方法平均了许多模型的最坏情况风险。这在概念上是混乱的，在计算上是缓慢的。
  2. 利用模型的结构: 通过利用指数族和共轭先验的数学特性，DRO-BAS\(_{PE}\) 将一个看似棘手的鲁棒优化问题转化为一个快速的单阶段凸规划。
  3. 速度 + 鲁棒性: 你不总是需要为了更好的结果而牺牲计算速度。对于适用的模型，DRO-BAS\(_{PE}\) 在这两个方面都占据优势。
  4. “PE” 形式更优: 虽然后验预测 (PP) 方法在直觉上讲得通，但后验期望 (PE) 方法产生了更好的数学性质 (凸性、闭式对偶) 和实验结果。

这项工作弥合了贝叶斯统计 (量化我们已知的内容) 与鲁棒优化 (保护我们免受未知内容影响) 之间的鸿沟。对于任何在有限数据上构建决策系统的人来说，用贝叶斯模糊集“对冲下注”看起来是制胜的策略。