如果你曾经在大型语言模型 (LLM) 之上构建过应用程序，你很可能遇到过某种令人费解的脆弱行为。你构建了一个措辞严谨的提示词 (Prompt) ，得到了很好的结果，然后——也许是不小心——你在提示词末尾添加了一个空格。突然之间，模型的输出完全变了。

为什么一个能够通过律师资格考试的系统会在一个空格键上栽跟头？

答案在于人类阅读文本的方式与现代 LLM 处理文本的方式之间存在根本性的脱节。人类看到的是字符；模型看到的是Token (代币) 。 这种脱节造成了研究人员所说的提示词边界问题 (Prompt Boundary Problem) 。

在这篇文章中，我们将深入探讨最近的一篇论文 “From Language Models over Tokens to Language Models over Characters” (从基于 Token 的语言模型到基于字符的语言模型) ，该论文提出了一种数学上原则性的解决方案来弥合这一鸿沟。我们将探讨如何将 Token 级别的概率转换为字符级别的概率，从而实现稳健、可预测的文本生成，而不会被一个多余的空格带偏。

问题的根源: Token 与字符

要理解这个问题，我们首先需要看看 LLM 是如何看待这个世界的。LLM 并不定义字符字符串 (如 “a”, “b”, “c”) 上的概率分布。相反，它在一个由分词器 (如字节对编码 BPE) 生成的 Token (整数) 词表上进行操作。

当你将字符串 “In the kingdom” 输入模型时，它首先被切分成块。

句子的 BPE Token 化示例。

如上所示，分词器将字符字符串转换为特定的整数序列。然后模型预测下一个整数。

提示词边界问题

这种紧张关系的产生是因为通常有多种方式来对一个字符串进行 Token 化，但模型通常是使用单一的“规范”Token 化方式进行训练和查询的。

考虑这个提示词: "In_the_kingdom_of_the_blind,_the" (其中 _ 代表空格) 。

如果我们要求模型使用贪婪解码 (选取可能性最大的下一个 Token) 来完成这个谚语，它会正确地预测 _one (Token ID 530) ，从而生成: “In the kingdom of the blind, the one-eyed man is king.” (山中无老虎，猴子称大王/盲人国里独眼称王) 。

然而，如果我们稍微调整一下提示词，添加一个末尾空格——"In_the_kingdom_of_the_blind,_the_"——Token 化结果就变了。最后一个 Token 不再是 the (Token 262) ；它可能变成 _the 与空格的组合，或者空格本身变成一个单独的 Token _ (Token 220) 。

带有末尾空格的 Token 化对比。

在论文中使用 GPT-2 的例子中，添加那个空格显著降低了目标词的概率。模型不再预测 “one”。相反，它预测了 “ills”，结果变成了: “…the ills of the world…” (世上的弊病) 。

这就是提示词边界问题 。 通过迫使模型在生成补全内容之前就锁定提示词的某种特定 Token 化方式，我们将它锁定在了一条可能并不代表字符最可能续写的路径上。

为什么“Token 修复”还不够

工程师们已经开发了一些启发式方法来修补这个问题。最常见的是 Token 修复 (Token Healing) 。 其思路很简单: 在生成之前，删除提示词的最后一个 Token，让模型重新生成它以及后续内容。这使得模型能够“修复”提示词与新文本之间的边界。

虽然对简单情况有效，但当一个单词以某种方式被分割成多个 Token，以至于回退一步无法修复时，Token 修复就会失效。

考虑提示词: "Hello, _worl"。 你希望模型将其补全为 "Hello, _world"。

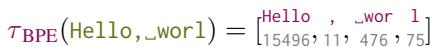
Hello, world 的 Token 化展示了被分割的 Token。

如上图所示，“world” 的 Token 化可能会被尴尬地分割。如果提示词以 worl 结尾，分词器可能会输出 [Hello, _, wor, l]。仅仅回退一个 Token (l) 不足以帮助模型意识到它本应该输出 Token world。模型被困在了 Token 空间中的低概率路径上，尽管这个字符序列非常常见。

解决方案: 覆盖 (Covering)

作者提出了一个严谨的解决方案: 我们不应该对提示词进行黑客式的修补，而应该在数学上将模型的 Token 概率转换为字符概率。

我们想要计算 \(p_{\Sigma}(\sigma)\)，即字符字符串 \(\sigma\) 的概率。 由于模型给我们的是 \(p_{\Delta}(\delta)\)，即 Token 字符串 \(\delta\) 的概率，我们需要一种方法在它们之间建立映射。

挑战在于，一个字符字符串可以由许多不同的 Token 序列表示。例如，字符 “a” 可能是 Token a，或者是 Token apple 的一部分，或者是 cat 的一部分。

定义覆盖

为了解决这个问题，作者引入了覆盖 (Covering) 的概念。

对于目标字符字符串 \(\sigma\)，覆盖 \(\mathcal{C}(\sigma)\) 是满足以下条件的所有 Token 序列的集合:

  1. 解码后的字符串以 \(\sigma\) 开头。
  2. 是“最小的”——意味着如果你移除最后一个 Token，它们就不再覆盖 \(\sigma\)。

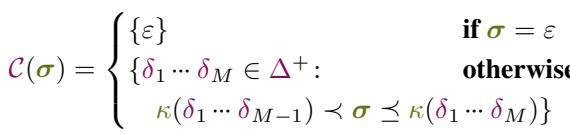
覆盖集的数学定义。

可以将覆盖想象为 Token 空间中的一个“前沿”。它代表了模型可能开始生成提示词中字符的所有可能的有效方式。

对于字符串 “Hello, worl”，覆盖将包括:

  • [Hello, _, world] (匹配 “Hello, world”，其以 “Hello, worl” 开头)
  • [Hello, _, wor, ld]
  • [Hell, o, _, world]

至关重要的是，覆盖考虑到了 Token 生成过程相对于字符字符串可能处于“Token 中间”的事实。

从 Token 概率到字符概率

一旦我们要了集合 \(\mathcal{C}(\sigma)\)，我们就可以计算字符字符串的前缀概率 。 这是覆盖中所有 Token 序列的总概率质量。

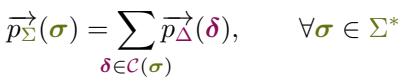
在覆盖上求和概率的公式。

这个公式就是桥梁。它的意思是: “字符字符串 \(\sigma\) 的概率是生成 \(\sigma\) 的每一个最小 Token 序列的概率之和。”

通过计算这个和，我们对所有可能的 Token 化方式进行了边缘化 (marginalize) 。模型是否“偏好”某种特定的 Token 化方式并不重要；如果所有有效 Token 化方式的总概率很高，那么该字符字符串就被认为是高概率的。

这有效地解决了提示词边界问题。无论你输入的是 “the” 还是 “the “，算法都会查看与这些字符兼容的所有 Token 序列，从而消除了特定分词器的脆弱性。

算法

准确计算这个和在计算上代价高昂，因为可能的 Token 序列数量会随着字符串长度呈指数级增长。然而，作者提出了高效近似的算法。

带剪枝的递归枚举

核心算法 enum_cover 递归地构建 Token 序列。它从一个空序列开始，尝试添加词表中的每一个 Token。

  1. 追加一个 Token。
  2. 解码序列为字符。
  3. 检查: 它是否匹配目标字符字符串 \(\sigma\)？
  • 如果偏离 (例如，目标是 “Hel” 而我们生成了 “Ha”) ，则丢弃。
  • 如果完全匹配或是前缀，则继续。
  • 如果它覆盖了目标 (比 \(\sigma\) 长) ，将其加入覆盖集。

由于词表很大 (通常 50k+ 个 Token) ，每一步都检查所有 Token 太慢了。作者使用了集束搜索 (Beam Search) 启发式算法来剪枝搜索空间。

在每一步，他们只保留前 \(K\) 个最可能的 Token 序列 (即“集束”) 。这是基于这样一个假设: 绝大多数概率质量集中在少数几种可能的 Token 化方式上，这对于自然语言来说通常是成立的。

打包集束求和 (Bundled Beam Summing)

为了让速度更快，研究人员实现了一种“打包”方法。他们不再追踪单独的 Token 序列，而是将概念上相似的序列分组打包。

他们使用 Trie 树 (前缀树) 来高效地查询语言模型以获取有效的下一个 Token。这允许他们批量过滤掉数千个无效 Token (那些与目标字符串中下一个字符不匹配的 Token) ，而不是逐一迭代。

这种优化使得算法相对于字符字符串长度以线性时间运行，使其在实时应用中变得可行。

实验结果

作者使用 Wikitext-103 数据集在四个开源模型 (包括 Llama-3 和 Phi-4) 上测试了他们的方法。他们旨在回答两个主要问题:

  1. 准确性: 集束搜索近似与“真实”分布有多接近？
  2. 性能: 它够快吗？

准确性 vs. 速度

他们测量了他们的近似方法 (使用小集束尺寸) 与高保真参考模型 (集束尺寸 \(K=128\)) 之间的 Jensen-Shannon 距离 (JSD)。

显示不同模型误差 (JSD) 与速度关系的图表。

图 1(a) 中的结果显示了明显的权衡。随着集束尺寸 (\(K\)) 的增加 (在 X 轴上向左移动) ，误差显著下降。

  • 速度: 小集束尺寸 (曲线右侧) 非常快，对于较小的模型每秒处理超过 100 字节。
  • 收敛: 误差很快趋于平稳。\(K=8\) 或 \(K=16\) 的集束尺寸就能提供非常准确的字符分布近似，更大的集束收益递减。

改善压缩率 (惊奇度)

最有趣的发现之一是这种方法如何影响惊奇度 (Surprisal) 。 惊奇度 (以比特/字节为单位) 本质上衡量了模型预测文本的能力。更低的惊奇度意味着更好的预测/压缩。

评估 LLM 的标准方法使用“规范 Token 化”——迫使模型评估分词器输出的特定 Token 序列。

显示惊奇度与速度关系的图表。

在图 1(b) 中，虚线水平线代表使用规范 Token 化的基线惊奇度。数据点代表字符级别的方法。

字符级别的方法始终实现了更低的惊奇度。

为什么？因为规范 Token 化是武断的。有时 Token 空间中的“拼写错误”或奇怪的单词分割实际上代表了正确的字符序列。通过对所有可能的 Token 化方式求和 (通过覆盖) ，模型因有效的预测而获得“加分”，而这些预测原本会被规范分词器惩罚。这表明 LLM 实际上是比我们需要中更好的文本模型——我们只是透过一个局限的视角在评估它们。

条件生成

最后，论文提供了一种条件 Token 生成算法。这取代了标准的生成循环。

\[p_{\Delta|\Sigma}(\delta | \sigma) \stackrel{\text{def}}{=} \mathbb{P}_{Y \sim p_{\Delta}} [ Y = \delta \mid \kappa(Y) \succeq \sigma ]\]

该算法不再仅仅采样下一个 Token，而是:

  1. 枚举提示词 \(\sigma\) 的覆盖。
  2. 根据概率比例从覆盖中采样一个 Token 序列 \(\delta\)。
  3. 从那里继续生成。

这保证了生成过程在数学上与字符提示词保持一致，有效地解决了本文开头说明的提示词边界问题。

结论

从“Token”到“字符”的转变似乎只是一个语义细节，但它解决了大型语言模型中的一个主要可用性缺陷。 提示词边界问题——即末尾空格会改变输出——是模型内部表示与用户输入之间不匹配的症状。

通过将 LLM 视为字符上的分布 (通过对 Token 进行边缘化计算) ，作者提供了一种与这些模型交互的方法，这种方法是:

  1. 稳健的: 不再有末尾空格导致的 Bug。
  2. 原则性的: 基于概率论，而不是像 Token 修复那样的启发式方法。
  3. 更好的: 实际上导致了更低的惊奇度得分。

对于学生和研究人员来说，这篇论文提醒我们，“标准”的做法 (规范 Token 化) 通常只是一种便利，而非基本真理。深入挖掘数学基础往往能揭示使用这些强大工具的更好、更稳健的方法。