如果你一直关注过去几年的生成式 AI 领域，目前的局势似乎很明朗: 扩散模型 (Diffusion Models) (如 Stable Diffusion 或 DALL-E) 和自回归模型 (Autoregressive Models) (如 GPT-4) 是赢家。它们能生成最高质量的图像和文本，主导了各大排行榜。

与此同时, 归一化流 (Normalizing Flows, NFs) ——这一以优雅的数学性质著称的模型家族——在很大程度上被遗忘了。虽然它们曾是密度估计的热门选择，但由于计算昂贵且无法生成我们在扩散模型中看到的高保真样本，它们逐渐名声扫地。

但是，如果归一化流并没有本质上的局限性呢？如果我们只是没能用正确的方式训练它们呢？

在一篇题为 “Normalizing Flows are Capable Generative Models” 的新论文中，来自 Apple 的研究人员证明了归一化流比以前认为的要强大得多。他们推出了 TARFLOW , 这是一种基于 Transformer 的架构，它在图像似然估计方面取得了最先进的结果，并且生成的样本可以与扩散模型相媲美。

在这篇文章中，我们将详细拆解 TARFLOW 的工作原理，使其具有可扩展性的具体架构变革，以及诸如“去噪”和“引导”等解锁其全部潜力的巧妙训练技巧。

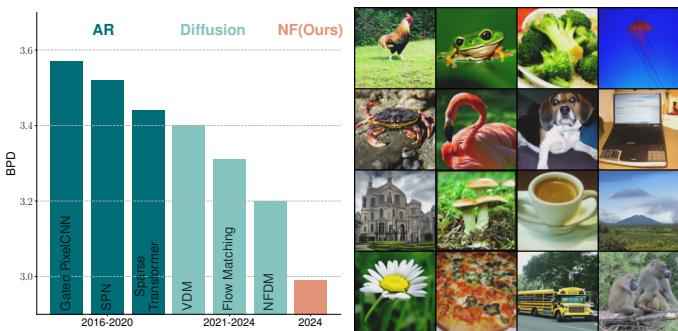
图 1. TARFLOW 在归一化流模型领域展示了巨大的进步，在密度估计和样本生成方面均达到了最先进的水平。左图: 我们展示了 ImageNet 64x64 上似然性能的历史进展，以每维比特数 (BPD) 衡量，我们的模型显著优于以前的方法 (详见表 2) 。右图: 我们训练的 ImageNet 128x128 模型生成的精选样本展示了归一化流模型前所未有的图像质量和多样性，为这类生成模型建立了新的基准。

归一化流的问题

要理解 TARFLOW 的重要性，我们首先需要了解归一化流的前提。

归一化流是一种生成模型，它学习复杂数据分布 \(x\) (如图像) 与简单先验分布 \(z\) (通常是标准高斯分布，即“噪声”) 之间的可逆映射 \(f\)。

训练目标是最大似然估计 (MLE) 。 由于映射是可逆的，我们可以利用变量变换公式 (Change of Variable formula) 计算数据的精确似然:

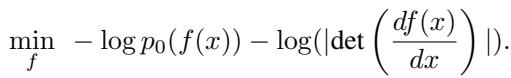
公式 1: 标准的归一化流目标函数。

如果我们假设先验 \(p_0\) 是标准高斯分布，该目标可以简化为最小化两项:

公式 2: 使用高斯先验的简化目标函数。

  1. 范数项 (Norm Term, \(0.5 \|f(x)\|^2_2\)) : 鼓励模型将数据样本映射到范数较小的潜向量 (使其靠近高斯分布的中心) 。
  2. 雅可比项 (Jacobian Term, \(-\log |\det|\)) : 防止模型“坍塌” (即防止将不同的输入映射到相同的输出) ，并鼓励其在潜空间中展开。

为什么它们举步维艰？

尽管拥有这些优美的数学性质，归一化流在可扩展性方面一直面临困难。以前的架构 (如 RealNVP 或 Glow) 依赖于特定的“耦合层”设计，以使雅可比行列式易于计算。然而，这些设计往往限制了模型的表达能力。相反，表达能力更强的方法 (如神经常微分方程 Neural ODEs) 往往数值不稳定或训练缓慢。

TARFLOW 通过将流框架与现代深度学习中最成功的架构——Transformer 相结合，挑战了这一现状。

TARFLOW 架构

TARFLOW 的核心是块自回归流 (Block Autoregressive Flow) 。

自回归流 (如较旧的 MAF 模型) 通常是逐像素工作的。为了预测像素 \(i\) 的变换，它们需要查看像素 \(0\) 到 \(i-1\)。TARFLOW 将其泛化为在图像的Patch (图块) 上工作，类似于视觉 Transformer (ViT) 。

从像素到 Patch

该模型不将图像视为像素网格，而是视为 Patch 序列。如果你有一张图像，它会被切分成序列 \(x\)。流模型一步步地转换这个序列。

该架构堆叠了多个“流块 (Flow Blocks) ”。如下图所示，这是一个深度的迭代过程:

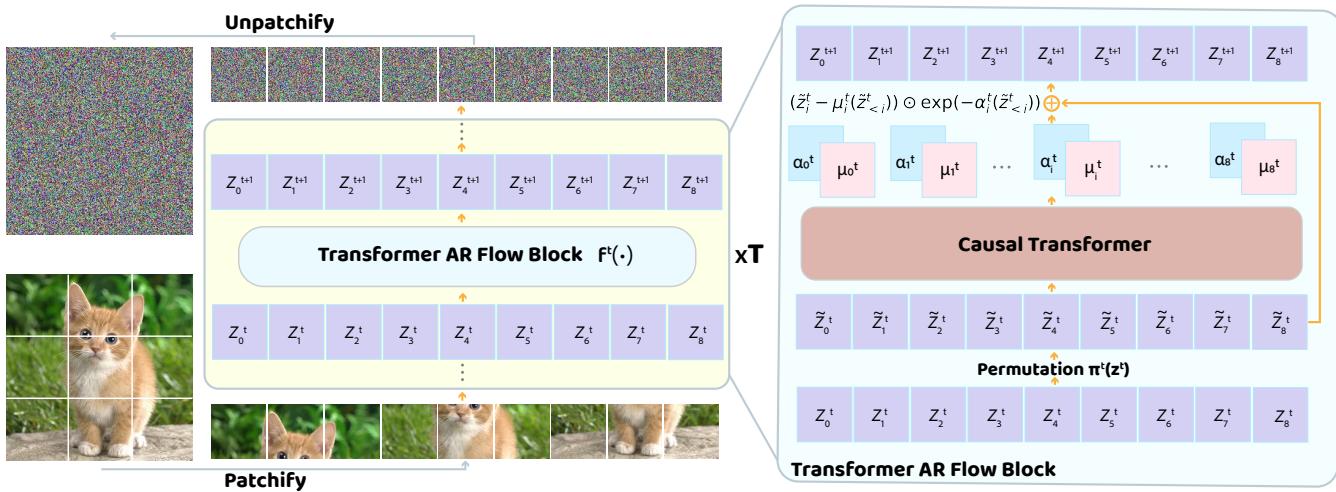
图 2. 左图: TARFLOW 由 T 个端到端训练的流块组成；右图: 每个流块的放大视图，包含序列排列操作、标准因果 Transformer 以及对排列后输入的仿射变换。

每个 Transformer 自回归流块包含三个主要步骤:

  1. 排列 (Permutation, \(\pi^t\)) : Patch 序列被重新排序。例如，如果第 1 层从左上到右下处理图像，第 2 层可能会反向处理。这使得信息能够在图像全局范围内传播。
  2. 因果 Transformer (Causal Transformer) : 一个标准的因果 Transformer (带有掩码注意力机制) 处理该序列。因为它是因果的，所以 Patch \(i\) 的变换仅依赖于当前顺序中位于其之前的 Patch。
  3. 仿射变换 (Affine Transformation) : Transformer 的输出预测用于变换输入潜变量 \(z^t\) 的参数 (\(\mu\) 和 \(\alpha\)) 。

前向传播

在前向传播中 (从数据到噪声) ，第 \(t\) 个块的变换如下所示:

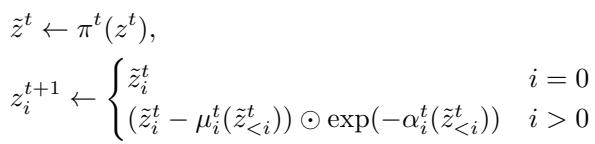
公式 3: 前向变换方程。

在这里，模型根据之前的 Patch 预测位移 (\(\mu\)) 和对数尺度 (\(\alpha\)) 。这些参数用于归一化当前的 Patch。

逆向传播 (生成)

生成图像涉及反转这个过程。我们采样噪声 \(z\) 并将其反向通过各层。逆向方程为:

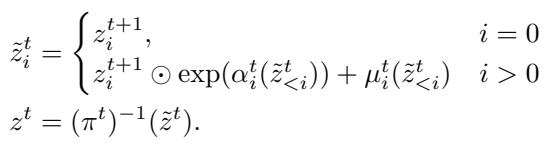
公式 4: 用于生成的逆向变换方程。

由于 Transformer 是因果的，我们可以逐个 Patch (或逐个块) 地生成图像。我们计算第一个 Patch 的参数，对其采样，将其反馈到 Transformer 中以获得第二个 Patch 的参数，依此类推。

这种架构使得 TARFLOW 易于扩展。你可以像扩大大语言模型 (LLM) 一样，简单地增加层数或加宽 Transformer。

三个提升质量的关键技术

仅有架构是不够的。作者引入了三个具体技术，让 TARFLOW 从“数学正确”变为“视觉惊艳”。

1. 高斯噪声增强 (Gaussian Noise Augmentation)

在标准的流模型训练中，通常会向连续输入添加“均匀反量化噪声” (大小约为一个像素区间的噪声) 。这可以防止模型坍塌到数字图像的离散值 (0, 1, … 255) 上。

然而，研究人员发现，对于感知质量而言，均匀噪声是不够的。相反，他们添加了幅度 (\(\sigma\)) 略大于像素区间大小的高斯噪声 。

为什么? 如果你不添加足够的噪声，逆模型 (生成器) 就是在非常稀疏的点集 (训练图像) 上训练的。当你尝试从连续的高斯先验中生成新图像时，模型会遇到“死区”，在这些区域它没有学到有意义的表示。添加高斯噪声有效地“抹平”或模糊了训练数据，为模型学习创造了一个更平滑的流形。

2. 基于分数的去噪 (Score-Based Denoising)

添加噪声有一个陷阱: 如果你在嘈杂的图像上训练，你的模型也会生成嘈杂的图像。样本看起来会有颗粒感。

为了解决这个问题，作者借用了扩散模型和基于分数的建模中的一个技巧: Tweedie 公式 。

Tweedie 公式允许你在给定噪声观测值 \(y\) 的情况下估计“干净”数据点 \(x\)，前提是你知道分数 (对数似然的梯度) 。公式如下:

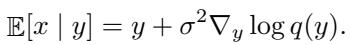
公式 11: 用于去噪的 Tweedie 公式。

美妙之处在于，归一化流可以显式计算似然 。 我们已经有了 \(\log p_{\text{model}}(y)\)。因此，我们可以利用模型自身的梯度对生成的样本进行去噪，而无需训练单独的去噪器！

完整的采样过程变为:

  1. 从先验中采样噪声 \(z\)。
  2. 将其通过流逆变换 \(f^{-1}\) 得到噪声图像 \(y\)。
  3. 应用去噪步骤得到干净图像 \(x\)。

公式 12: 带有去噪的完整采样过程。

这项技术的视觉效果是巨大的。在下图中，请看“原始样本” (上) 和“去噪后” (下) 的区别。

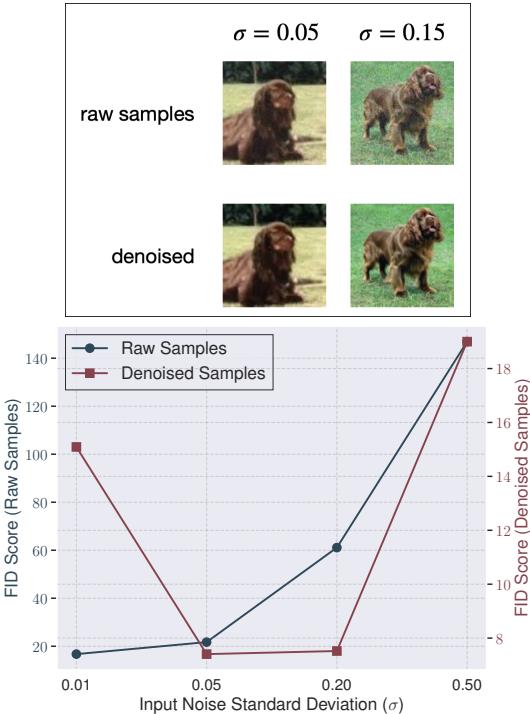
图 4. 上图: 输入噪声 \\(\\sigma\\) 和去噪的效果，所有样本均在 ImageNet 128x128 上以引导权重 w = 2 生成，源自相同的初始噪声，放大查看效果更佳。下图: ImageNet 64x64 上样本 FID 与输入噪声 \\(\\sigma\\) 的关系 (含去噪与不去噪) 。在去噪之前，看似较小的 \\(\\sigma\\) 具有最佳 FID，这是因为原始样本中存在的噪声较少。然而，在使用公式 8 进行去噪后，稍大的 \\(\\sigma\\) 有利于获得更好的 FID 并展示更一致的形状。注意右侧 y 轴的刻度与左侧不同。

如上图 (图 4 底部) 所示，在去噪之前 (蓝线) ，增加噪声会损害质量。去噪之后 (红线) ，增加噪声实际上提高了质量，前提是你最后清理了它。

3. 引导 (适用于流模型的 CFG)

让文本到图像模型风靡一时的关键特性之一是无分类器引导 (Classifier-Free Guidance, CFG) 。 这项技术将生成过程推向特定的类别条件 (或提示词) ，并远离通用的、无条件的预测。它以牺牲多样性为代价换取了保真度。

作者表明, 引导技术同样适用于归一化流 。

他们修改了逆向流步骤。他们不直接使用预测的 \(\mu\) 和 \(\alpha\)，而是计算一个“引导”版本。这是通过取条件预测 (例如“狗”) 和无条件预测 (空上下文) 之间的差值，并用权重 \(w\) 放大来实现的。

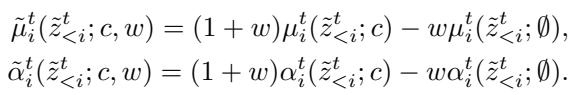
公式 14: 计算引导参数的方程。

从视觉上看，增加引导权重 \(w\) 将模糊、嘈杂的团块变成了清晰、可识别的对象。

图 7. 左图: 在 ImageNet 128x128 上使用类条件模型改变引导权重，此处展示了 ImageNet 类别 849 (“茶壶”) 的 4 个样本；右图: 无条件 ImageNet 64x64 模型的引导权重和注意力温度的变化。

实验结果

那么，TARFLOW 与竞争对手相比如何呢？

似然估计

似然 (以每维比特数或 BPD 衡量) 是衡量概率模型拟合数据程度的“最纯粹”指标。数值越低越好。

TARFLOW 在 ImageNet 64x64 上取得了最先进的结果 (SOTA) , 首次突破了 3.0 BPD 的大关。它显著优于以前的流模型 (如 Glow 和 Flow++) ，甚至在原始密度估计方面击败了现代扩散/流匹配模型。

表 2. 无条件 ImageNet 64x64 测试集上的每维比特评估。我们用 [P-Ch-T-K- \\(p_{\\epsilon}\\) ] 格式表示 TARFLOW 配置。

图像生成

虽然似然性对科学研究很有意义，但我们更关心漂亮的图片。衡量图像逼真度的标准指标是 Fréchet Inception 距离 (FID) (越低越好) 。

利用上述技术 (高斯噪声 + 去噪 + 引导) ，TARFLOW 生成的样本可以与扩散模型相媲美。

表 3. 条件 ImageNet 64x64 上的 Fréchet Inception 距离 (FID) 评估。我们用 [P-Ch-T-K- \\(p_e\\) ] 格式表示 TARFLOW 配置。

有趣的是，TARFLOW 的采样过程在视觉上类似于扩散模型。因为它逐个 Patch (或通过在潜空间中的迭代细化) 构建图像，你可以看着图像从噪声中浮现。

图 8. 从左到右，拥有 8 个流块的模型在 ImageNet 128x128 上的采样轨迹。可视化包含了最终的去噪步骤。

为什么这很重要

多年来，研究界一直认为，与扩散模型相比，归一化流在生成能力上有着内在的局限性。这篇论文表明，这种差距并非本质上的——而是架构和方法论上的。

通过采用 Transformer 骨干 (可扩展性) ，确定高斯噪声的重要性 (平滑流形) ，并实施基于分数的去噪 (清理输出) ，TARFLOW 让归一化流重回大众视野。

这令人兴奋，因为归一化流提供了扩散模型所不具备的特性，例如精确的似然计算以及数据和潜变量之间的确定性映射。有了 TARFLOW，我们可能会看到流基模型在高保真生成任务中的复兴。

关键要点:

  • 架构: Transformers 适用于任何地方，包括归一化流。
  • 噪声策略: 训练期间使用高斯噪声比均匀噪声更有利于感知质量，但需要去噪步骤。
  • 去噪: 你可以使用流模型自身的似然梯度来“自我修正”输出。
  • 引导: 无分类器引导不仅适用于扩散模型；它也能显著提升流模型的保真度。

TARFLOW 证明，只要有正确的设计选择，这个被“遗忘”的生成模型家族完全有能力达到最先进的性能。