预测未来很难。准确预测关键事件——比如机器零件故障，或者更重要的临床试验中病人的生存时间——何时发生则更为困难。在高风险领域如医疗保健中，简单的“最佳猜测”是不够的。医生和病人需要了解该猜测的不确定性。他们需要一个保证: “我们有 90% 的把握确信病人至少能存活 \(X\) 个月。”

在机器学习 (ML) 领域, 共形预测 (Conformal Prediction) 已成为提供这些严格统计保证的黄金标准。然而，将其应用于生存分析历来受到一个棘手的数据问题的困扰，即*删失 (censoring) *。

在这篇文章中，我们将深入探讨 Matteo Sesia 和 Vladimir Svetnik 的一篇研究论文，题为 “Doubly Robust Conformalized Survival Analysis with Right-Censored Data” (右删失数据下的双重稳健共形化生存分析) 。 我们将探索他们如何使用一种巧妙的插补策略解决生存分析中的“数据缺失”问题，从而创建一种即使在我们的模型不完美时也能保持可靠的方法。

问题所在: 生存分析与缺失的时钟

要理解这篇论文的贡献，我们首先需要了解生存分析独特的数据环境。

在标准的回归问题 (如预测房价) 中，训练集里的每栋房子你都知道最终的售价。在生存分析中，我们的目标变量 \(T\) 是直到事件发生 (例如死亡或复发) 的时间。然而，我们通常无法观察到每个人的 \(T\)。

有些病人退出了研究。有些人在研究结束时还活着。对于这些人，我们不知道他们真实的生存时间 \(T\)；我们只知道他们至少存活到了某个时间 \(C\) (删失时间) 。

这就产生了一个数据集，对于每个个体 \(i\)，我们观察到一个特征向量 \(X_i\) (年龄、血压等) 和一个观察时间 \(\tilde{T}_i\)，它是真实事件时间和删失时间的最小值。我们还有一个指示器 \(E_i\) 告诉我们观察到的是哪一个。

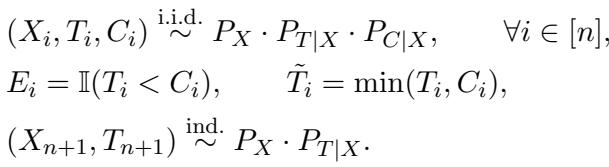
生存分析中观测数据的数学公式。

如上式所示，如果事件发生了 (\(E_i=1\)) ，我们看到的是真实时间 \(T\)。如果病人被删失了 (\(E_i=0\)) ，我们只看到 \(C\)。

令人头疼的删失问题

共形预测领域的最新进展 (由 Candès, Lei, 和 Gui 等研究人员推动) 已成功为生存时间创建了预测下界 (Lower Prediction Bounds, LPBs) 。LPB 是一个值 \(\hat{L}(X)\)，我们可以保证以 \(1-\alpha\) (例如 90%) 的概率，真实的生存时间 \(T\) 大于 \(\hat{L}(X)\)。

然而，之前的方法主要依赖于一种更简单的场景，称为 I型删失 (Type-I Censoring) 。 在 I型删失中，研究的“结束时间”对每个人都是固定且已知的。如果病人去世，我们知道他们去世的确切时间，并且我们知道如果他们还活着，他们本来会在何时被删失 (通常是研究结束日期) 。

然而，现实世界的数据通常呈现右删失 (Right-Censoring) 。 在这里，如果病人经历了事件 (\(T < C\)) ，我们看到了事件时间，但我们不知道他们本来会在何时被删失 。 也许他们第二天就会退出；也许他们会待上几年。那个值 \(C\) 是潜在的 (隐藏的) 。

这种信息的缺失破坏了标准的共形预测算法。如果你不知道数据分布的全貌，你如何校准你的不确定性呢？

解决方案: DR-COSARC

Sesia 和 Svetnik 介绍了 DR-COSARC (右删失数据下的双重稳健共形化生存分析) 。该方法的核心理念是两步走的“插补与校准”方法。

如果问题在于我们要为去世的人补全未知的删失时间 \(C\)，那为什么不使用机器学习来进行有根据的猜测呢？

第一步: 插补技巧

研究人员假设“条件独立删失”，这意味着给定病人的特征 \(X\)，生存时间 \(T\) 和删失时间 \(C\) 是独立的。这允许他们在训练标准生存模型的同时，训练一个 删失模型 (\(\hat{\mathcal{M}}^{\mathrm{cens}}\)) 。

删失模型学习的是病人退出或研究结束的概率分布。

该算法遍历校准数据 (用于调整不确定性界限的数据) 。对于被删失的病人 (\(E_i=0\)) ，我们已经知道了 \(C_i\)，所以保留它。对于经历了事件的病人 (\(E_i=1\)) ，算法会插补一个合成的删失时间 \(\hat{C}_i\)。

至关重要的是，我们不能随便选一个数字。我们知道对于这些病人，删失时间必须大于他们死亡的时间 (\(C > T\)) 。该方法从估计的条件分布中采样一个新的删失时间，且该值被限制为大于观察到的事件时间 \(\tilde{T}_i\)。

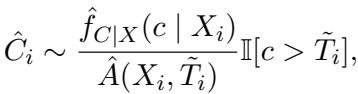
采样合成删失时间的公式。

在上式中，\(\hat{f}_{C|X}\) 是删失时间的估计概率密度。为了使其成为有效的概率，他们通过删失时间大于观察到的事件时间 \(\tilde{T}_i\) 的概率对其进行归一化:

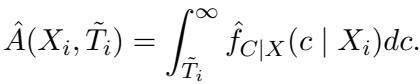
插补积分的归一化常数。

通过执行这种插补，研究人员将杂乱的右删失数据集转换为合成的I型删失数据集。一旦数据变成这种格式，就可以应用现有的共形预测机制了。

第二步: 共形校准

有了“完整”的数据集，DR-COSARC 应用加权共形推理。它使用生存模型生成原始分数 (比如预测的中位生存时间) ，然后计算一个截断调整值，以确保在校准数据上达到 90% 的覆盖率。

该论文整合了两种主要的校准方法:

  1. 固定截断值 (Fixed Cutoffs) : 预测病人是否存活超过单一、固定的时间点。
  2. 自适应截断值 (Adaptive Cutoffs) : 针对每个病人的具体风险状况预测生存时间。作者通常推荐这种自适应方法，因为它提供了信息量更大 (更紧凑) 的界限。

“双重稳健”的安全网

DR-COSARC 中的 “DR” 代表 双重稳健 (Doubly Robust) 。 这是一个强大的理论属性。在统计估计中，双重稳健通常意味着你有两个模型 (这里是生存模型和删失模型) ，只要其中任何一个是正确的，你的最终结果就是有效的。

  1. 场景 A: 你的生存模型很完美，但你的删失模型 (以及插补) 很糟糕。该方法仍然有效，因为生存模型已经知道了关于 \(T\) 的真相。
  2. 场景 B: 你的生存模型很糟糕 (这是个难题！) ，但你的删失模型很好。该方法仍然有效，因为共形校准使用来自删失模型的准确权重来修正生存模型的错误。

这通过数学证明形式化，证明了覆盖概率收敛于目标 \(1-\alpha\):

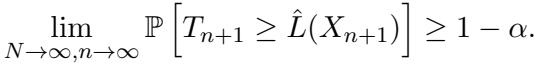
显示覆盖率渐近有效性的极限方程。

随着样本量的增加，这种有效性在渐近意义上成立，为在不确定环境中使用此工具的研究人员提供了强大的安全网。

实验结果

作者针对几个基准测试了 DR-COSARC，包括“先知 (Oracle) ” (拥有完美知识) 、“未校准 (Uncalibrated) ”模型，以及一种忽略右删失复杂性的共形预测“朴素 (Naive) ”应用 (Naive CQR) 。

他们生成了具有不同难度的合成数据。

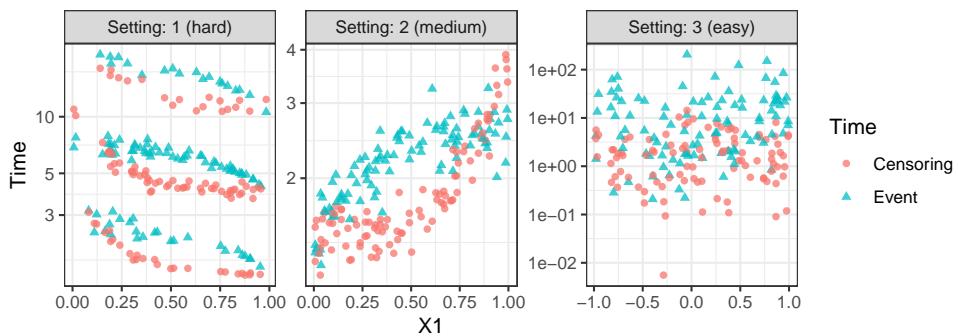
可视化合成数据分布。

如上图 Figure A1 所示，数据模拟了协变量 (\(X\)) 和时间之间的复杂关系。“设置 1”特别棘手，旨在使拟合准确的生存模型变得非常困难。

合成数据上的表现

Figure 1 (下图) 中的结果令人印象深刻，尤其是在困难的“设置 1” (第一行) 中。

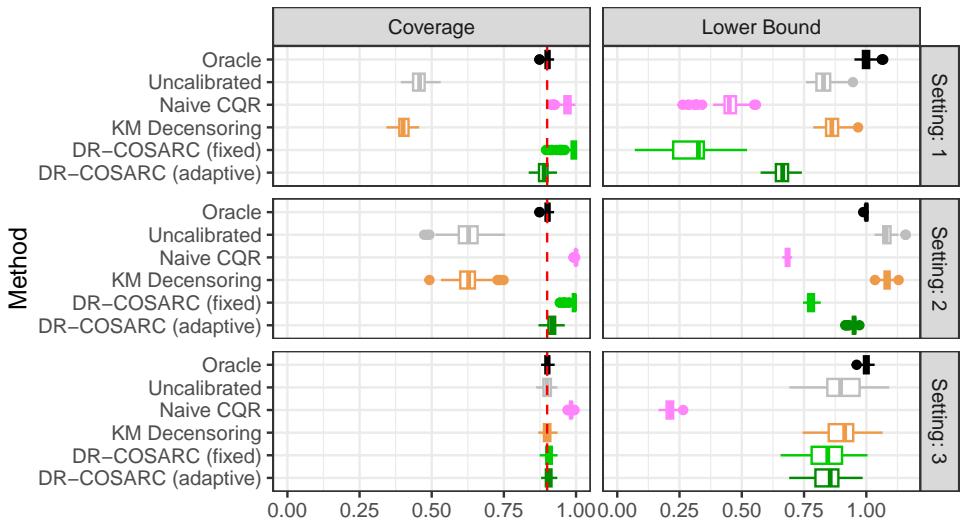
比较各方法在合成数据上的表现，显示覆盖率和下界长度。

  • 覆盖率 (左列) : 看左上角的图。“未校准”方法 (灰色) 惨败，覆盖率远低于要求的 90%。“朴素 CQR” (粉色) 在技术上覆盖率足够，但它是通过毫无用处的保守 (给出极小的界限) 来实现的。然而, DR-COSARC (绿色方块和星星) 即使在这个困难的设置中，也紧贴着红色虚线 (目标 90% 覆盖率) 。
  • 下界 (右列) : 我们希望这些值高一些 (信息量大) 。预测“你将存活至少 0 天”是有效的，但毫无用处。DR-COSARC 提供的界限与“先知”具有竞争力，在保持安全性的同时最大化了信息量。

证明双重稳健性

为了通过实证证明“双重稳健”的主张，作者进行了一项实验，他们通过改变可用的训练样本数量来故意改变删失模型的质量，同时保持生存模型不变。

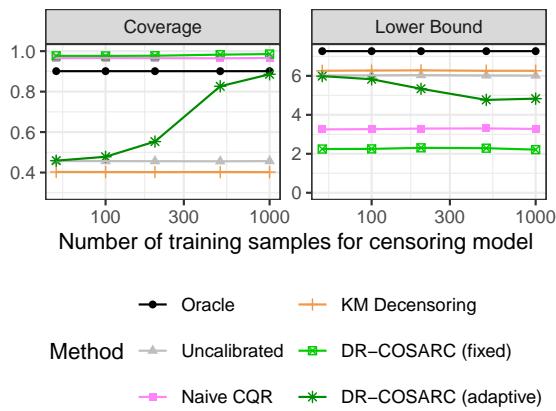
表现随删失模型训练样本数量变化的函数关系。

在 Figure 2 (上图) 中，特别是在困难的设置 1 (已知生存模型表现挣扎) 中，我们看到了删失模型的力量。随着删失模型训练样本数量的增加 (x 轴) ，DR-COSARC (绿线) 的覆盖率攀升至目标的 90%。

这证实了理论: 当生存模型较弱时，一个好的删失模型可以拯救该方法。

现实世界应用

最后，研究人员将 DR-COSARC 应用于七个现实世界的医疗数据集，包括肺癌 (VALCT) 、乳腺癌 (METABRIC) 和心脏移植 (HEART) 的研究。

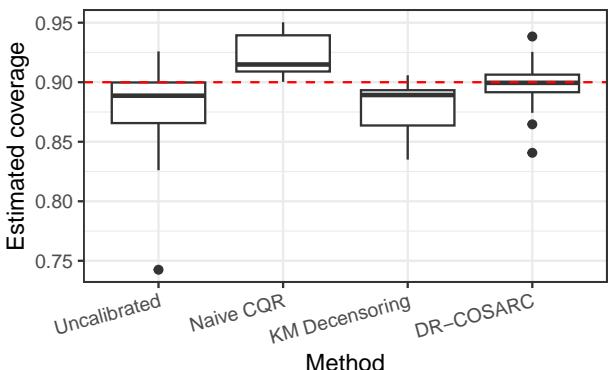
现实世界数据集上的估计覆盖率。

在 Figure 3 中，我们看到了这些数据集中估计覆盖率的分布。“未校准”方法通常低于 0.90 的目标 (红色虚线) ，给病人带来了风险。DR-COSARC (最右边的箱线图) 始终将其重心集中在目标之上或正好在目标上，在不同的医疗背景下提供了可靠、安全的预测。

为什么这很重要

生存分析正从简单的 Cox 比例风险模型转向复杂的机器学习模型，如随机生存森林和深度神经网络。这些模型很强大，但往往是过度自信的“黑盒”。

DR-COSARC 弥合了这一差距。它允许研究人员使用强大的 ML 模型来预测生存情况，同时保持临床决策所需的统计严谨性。通过插补解决右删失的“盲点”，它确保我们既不会丢弃经历了事件的病人的宝贵数据，也不会对那些被删失的病人做出无效的假设。

“双重稳健”属性更是锦上添花——它承认在现实世界中，模型很少是完美的。通过只要求两个组件中的一个准确，DR-COSARC 为现代生存分析提供了一个有弹性且实用的工具。

本文总结了 Matteo Sesia 和 Vladimir Svetnik 的论文 “Doubly Robust Conformalized Survival Analysis with Right-Censored Data”。