引言

在计算化学的革命中，机器学习 (ML) 已成为新的光剑。它斩断了密度泛函理论 (DFT) 和量子力学所带来的沉重计算成本，使研究人员能够以极快的速度模拟比以往更大、时间更长的系统。其前提很简单: 训练一个神经网络来预测原子如何相互作用，你就可以模拟从药物发现到电池材料的所有内容。

然而，当我们追求更快、更可扩展的模型时，关于我们在这些网络上施加的“物理定律”出现了一场根本性的争论。传统上，原子间作用力被计算为势能的导数——这种方法保证了能量守恒。但新一波“非保守”模型表明，我们可以跳过能量计算，直接预测力，从而用物理严谨性换取计算速度。

在研究论文**“The dark side of the forces”**中，Filippo Bigi、Marcel F. Langer 和 Michele Ceriotti 调查了这种权衡是否值得。他们揭示了忽视能量守恒的重大危险，证明了“直接力”模型可能导致灾难性的模拟失败。但他们也提供了一条出路: 一种混合方法，既能利用黑暗面的速度，又不会屈服于其不稳定性。

物理原理: 势能与直接力预测

要理解这场争议，我们需要回顾一点经典力学。在原子模拟中，原子的行为由势能面 (PES) 控制，表示为 \(V\)。

作用在原子上的力 \(\mathbf{f}\) 定义为该势能相对于原子位置 \(\mathbf{r}\) 的负梯度 (斜率) :

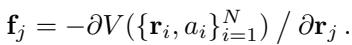
因为力是从标量能量场推导出来的，所以它是保守的 。 这意味着如果你让原子沿闭合回路移动并使其回到起点，所做的总机械功为零。能量既不会凭空产生，也不会凭空消失；它是守恒的。

计算瓶颈

在神经网络的背景下，强制执行这种关系是有代价的。为了得到力，你首先要预测能量 \(V\)，然后使用自动微分 (反向传播) 来计算导数 \(\partial V / \partial \mathbf{r}\)。

虽然有效，但这一反向传播步骤计算昂贵——通常会使推理成本相比简单的正向传播增加 2 到 3 倍。

为了绕过这一瓶颈，最近的架构 (如 ORB、Equiformer 等) 提出在正向传播中直接预测力向量 \(\mathbf{f}\)，完全忽略底层的能量 \(V\)。这在实现上更快、更简单。然而，通过切断力与能量之间的联系，这些模型不再保证能量守恒。它们变成了非保守模型。

诊断“黑暗面”

我们如何衡量一个模型是否打破了物理定律？研究人员建议检查力的雅可比矩阵 (Jacobian matrix) \(\mathbf{J}\)。如果力是能量的导数，那么二阶导数矩阵 (海森矩阵) 必须是对称的 (\(J_{ij} = J_{ji}\)) 。

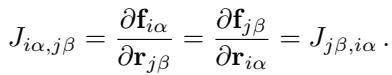
如果模型直接预测力，这种对称性就不会被强制执行。研究人员定义了一个指标 \(\lambda\)，通过测量雅可比矩阵的不对称性来量化模型的“非保守”程度。

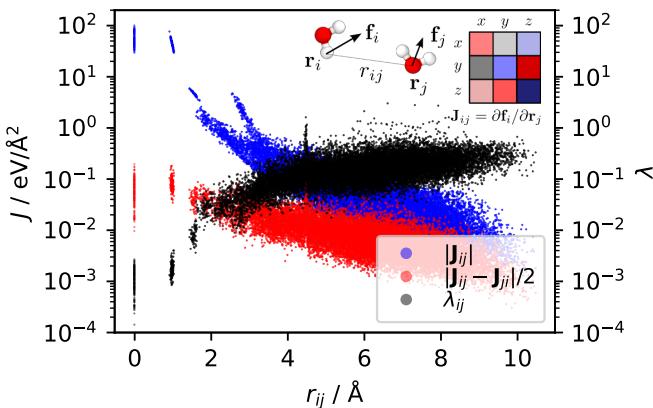
如图 1 所示，不对称性 (由 \(\lambda\) 测量) 并不会随着距离增加而消失。事实上，对于远距离原子间的相互作用 (蓝点) ，非保守成分 (不对称性) 通常与相互作用本身一样大。这表明非保守伪影遍布于分子的空间相互作用中。

为了直观地展示这一点，作者计算了当沿闭合路径移动原子时不同模型所做的功。

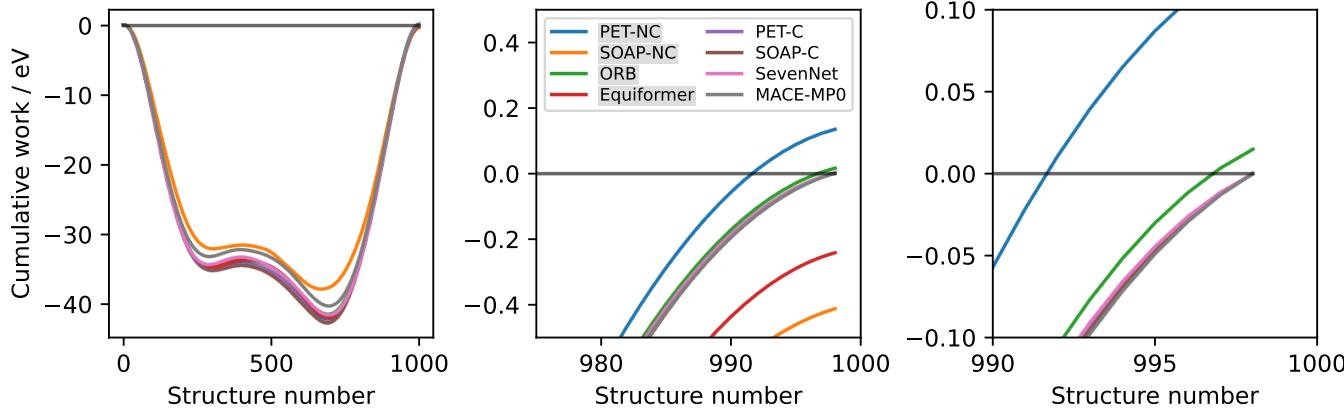
在图 6 中，你可以清楚地看到差异。保守模型 (如 PET-C 和 SOAP-BPNN-C) 在闭合回路结束时积分功正好为零。然而，非保守模型 (如 ORB 和 PET-NC) 产生了一个非零值。它们实际上仅仅通过让原子绕圈移动，就凭空制造 (或消灭) 了能量。

后果: 爆炸性的模拟

有人可能会争辩说，如果模型速度够快，能量守恒中的小误差是可以接受的。然而，该论文表明，这些“小”误差在分子动力学 (MD) 模拟中会迅速累积。

无限加热问题 (NVE 系综)

在 NVE 模拟 (粒子数、体积和能量恒定的孤立系统) 中，系统应保持稳定的温度。

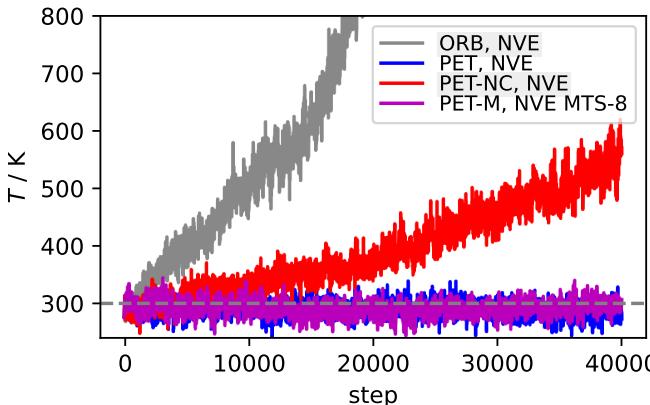
图 2 揭示了非保守模型在这种设置下的灾难性失败。

• 蓝线 (PET): 保守模型保持稳定的温度 (在初始平衡后) 。
• 灰线和红线 (ORB, PET-NC): 非保守模型表现出失控的加热效应。

因为非保守力不断向系统注入虚假的功，原子的运动速度越来越快。论文指出，对于 PET-NC 模型，这种漂移对应于每秒 7000 亿度的加热速率。这使得直接力模型对于标准的能量守恒模拟几乎毫无用处。

热库陷阱 (NVT 系综)

一个常见的反驳观点是，大多数模拟使用热库 (NVT 系综) 来保持温度恒定，这应该能抽走多余的热量。

研究人员通过应用激进的朗之万 (Langevin) 热库对此进行了测试。虽然强力热库可以保持温度稳定，但它们引入了一个新问题: 它们破坏了系统的动力学性质。

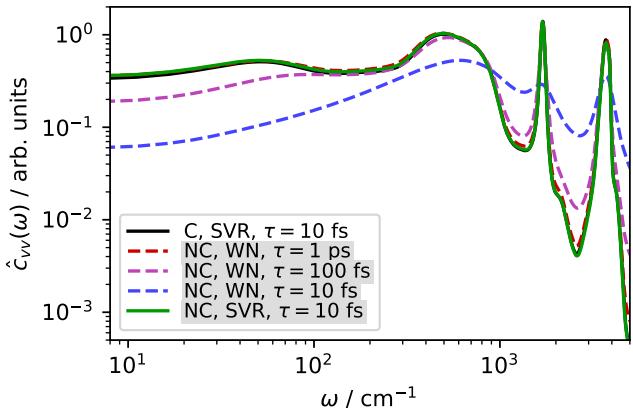
图 3 显示了速度功率谱 (这与原子如何振动和扩散有关) 。

• 黑线: 保守模型参考线。
• 绿/蓝/紫线: 使用不同热库的非保守模型。

为了防止非保守模型爆炸，热库必须非常激进 (\(\tau=10\) fs) ，以至于它抑制了水分子的自然运动 (绿线) ，显著改变了扩散系数。你实际上是为了修正数学问题而冻结了物理过程。

解决方案: 两全其美

作者得出的结论是，虽然纯粹的非保守模型对模拟来说是危险的，但直接力预测的计算速度太有价值了，不应完全放弃。他们提出了两种混合策略，以安全地利用“并不完美”的直接力。

1. 快速预训练，保守微调

你可以在训练的繁重任务阶段利用直接力预测的速度。策略如下:

1. 训练一个模型直接预测力 (训练速度快，无反向传播开销) 。
2. 获取该预训练模型并添加一个“能量头 (energy head) ”。
3. 使用严格的、保守的反向传播方法对模型进行几个周期的微调 (Fine-tune) 。

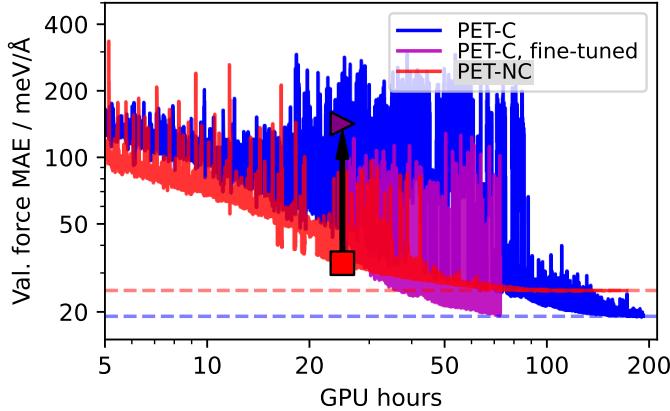
图 14 展示了这种方法的威力。品红线 (微调版) 达到了与完全保守模型 (蓝线) 相同的低误差，但仅消耗了一小部分 GPU 时间。这使得研究人员能够高效地训练大规模的“基础模型”，而无需牺牲物理有效性。

2. 多重时间步长 (MTS)

在运行模拟时，作者建议使用多重时间步长 (Multiple Time Stepping) 。 在该方案中，你使用廉价的、非保守的力进行大部分积分步骤 (“快”内循环) ，并周期性地用昂贵的、保守的力进行校正 (“慢”外循环) 。

通过每 8 步 (\(M=8\)) 才评估一次昂贵的保守力，模拟保持了稳定和物理上的准确性，同时运行速度几乎与非保守模型一样快。

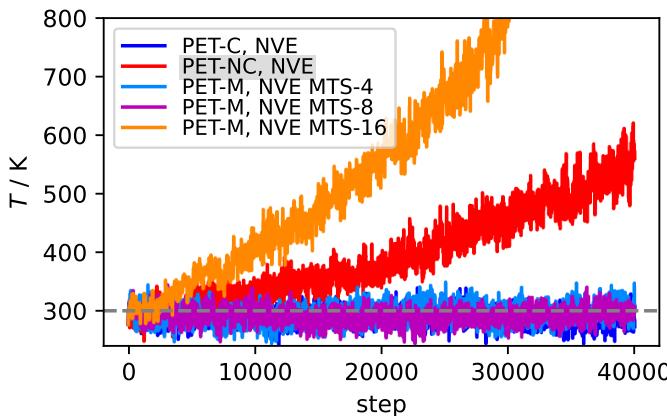
图 16 证明了 MTS 的有效性。虽然纯非保守模型 (红线) 的温度失控上升，但 \(M=8\) 的 MTS 模拟 (紫线) 保持完美稳定，与完全保守的基线 (蓝线) 难以区分，但速度明显更快。

结论

“黑暗面”的诱惑——为了节省计算成本而直接预测力——在机器学习中非常强烈。然而，这项研究强调，放弃能量守恒并非无害的近似；它从根本上破坏了分子模拟的力学机制，导致非物理加热和扭曲的动力学。

好消息是，我们不必在速度和物理学之间做选择。通过将直接力预测视为一种加速工具 (通过预训练或多重时间步长) ，而不是作为势能的替代品，我们可以构建既快如闪电又在物理上合理的下一代原子模型。