引言

大语言模型 (LLM) 最迷人的能力之一就是上下文学习 (In-Context Learning, ICL) 。 你只需给模型几个示例——比如“苹果 -> 红色，香蕉 -> 黄色”——突然之间，无需任何权重更新或重新训练，它就能理解模式并预测出“酸橙 -> 绿色”。对我们来说，这感觉很直观。但对机器学习研究人员来说，这在数学上令人困惑。一组静态的权重是如何即时适应新任务的？

最近的研究表明，Transformer 将这些任务表示为其隐藏状态中的“向量”。可以把它想象成模型大脑中代表“翻译”或“情感分析”的一个坐标。但是，知道这些向量存在并不能解释它们是如何到达那里的，或者为什么它们在某些任务上比其他任务表现更好。

在这篇文章中，我们将深入探讨论文 “Emergence and Effectiveness of Task Vectors in In-Context Learning: An Encoder Decoder Perspective” (上下文学习中任务向量的涌现与有效性: 编码器-解码器视角) 。 这项研究层层剖析 Transformer，揭示了一种两步机制: 任务编码 (Task Encoding) (识别任务) 和任务解码 (Task Decoding) (执行算法) 。

我们将探索模型如何在训练过程中在其“思维”中分离不同的概念，为什么微调前几层实际上比微调后几层更有效，以及我们如何通过观察其内部表示的几何形状来从数学上预测模型的性能。

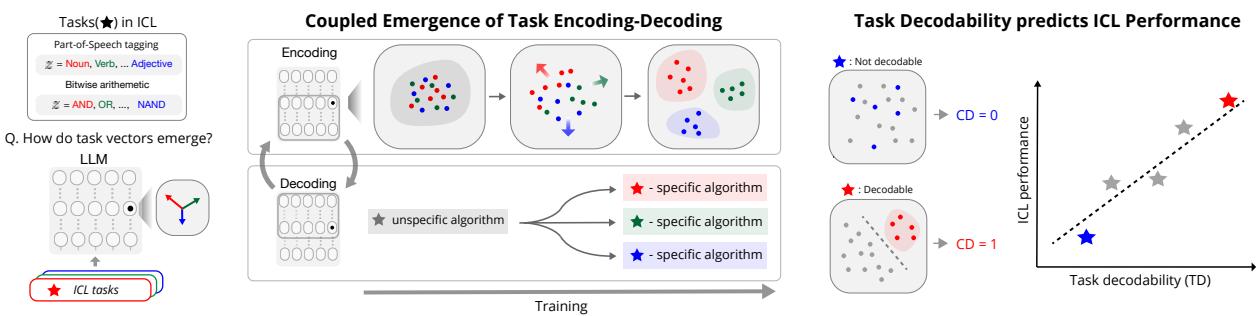
图 1. 我们工作的概览。我们研究任务编码-解码，以解释任务向量为何以及如何在预训练 LLM 中涌现。

背景: 作为贝叶斯推断的 ICL

要理解这一机制，我们首先需要看看理论框架。研究人员采用了上下文学习的贝叶斯视角 。

想象一下，你正在看一串数字: 2, 4, 6… 你需要猜下一个数字。

  1. 首先，你无意识地推断出潜在概念 (\(z\)) : “规则是偶数。”
  2. 其次，你应用该规则生成预测 (\(y\)) : “下一个数字是 8。”

论文认为 Transformer 执行的正是这种两阶段过程。在数学上，它看起来像这样:

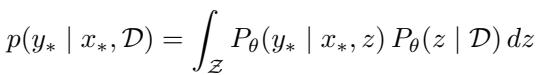
描述 ICL 为两阶段贝叶斯过程的公式 1。

这里，\(P_\theta(z | \mathcal{D})\) 代表任务编码阶段: 模型观察上下文示例 (\(\mathcal{D}\)) 并找出潜在任务 \(z\)。 然后，\(P_\theta(y_* | x_*, z)\) 代表任务解码阶段: 模型使用该任务信息 (\(z\)) 生成正确的输出 \(y_*\)。

研究人员假设这不仅仅是一个数学抽象——它是物理上发生在神经网络层内部的过程。模型将任务编码成一个特定的向量 (表示) ，然后“解码”该向量以触发特定的算法。

核心方法: 研究合成任务

为了证明这一理论，作者从一个受控环境开始。他们在稀疏线性回归混合 (Mixture of Sparse Linear Regression) 任务上训练了一个小型 Transformer (GPT-2 架构) 。

通俗地说: 模型被展示了由不同的隐藏数学规则 (基，bases) 生成的数字序列。它的工作是找出使用了哪条规则并预测下一个数字。因为研究人员创建了数据，所以他们确切地知道任何时候哪个“潜在任务”是活跃的。

编码与解码的耦合涌现

模型学习时内部发生了什么？结果令人震惊。模型并不是平滑均匀地学习所有内容。相反，它表现出了突然的“相变”。

图 2. 稀疏线性回归混合中任务编码和条件解码算法的耦合涌现。

让我们分解上面的图 2 , 这对于理解这一现象至关重要:

  1. 损失曲线 (左) : 看红线 (\(B_1\)) 。误差在特定点 (标记为 a, b, c) 急剧下降。这表明模型突然“开窍”了。
  2. 几何形状 (右) : 这些 UMAP 图展示了模型对数据的内部表示。
  • 在点 (a): 这些点是一团乱麻。模型无法区分不同的数学规则。
  • 在点 (b): 橙色聚类分离了出来。这与损失的第一次下降相吻合。模型已经学会了将“任务 1”与其他任务区分开来。
  • 在点 (c): 所有聚类都清晰可辨。模型在其潜在空间中完全分离了这些任务。

这证实了任务编码-解码假设。一旦模型成功将任务的表示与其他任务分离开来，它才能解决该任务 (降低损失) 。随着编码变得更清晰 (聚类分离) ，解码 (性能) 也随之提高。

如果我们观察随时间推移各层的表示，可以更清楚地看到这种演变:

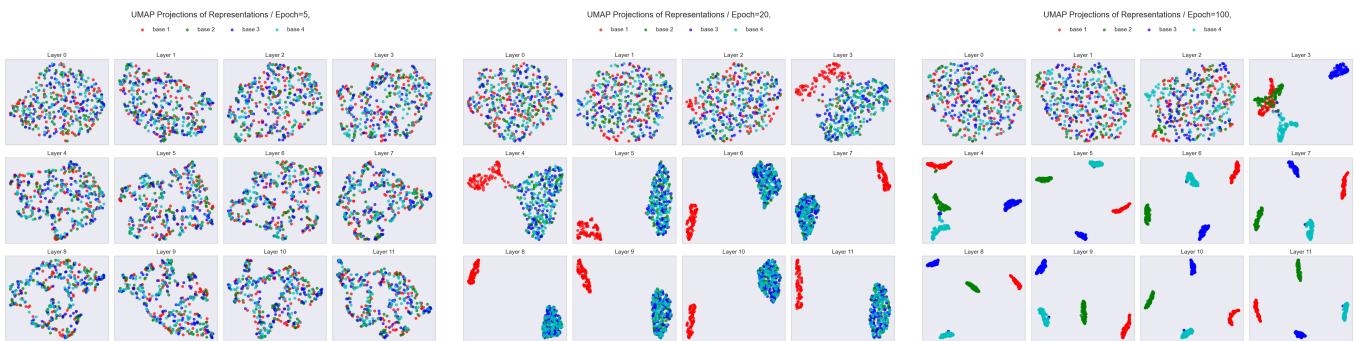
图 11. 合成稀疏线性回归任务训练过程中各层表示的 UMAP 可视化。

在图 11中，注意Epoch 20 。 在早期层 (0-3) ，表示是混合的。但在第 4-5 层左右，它们开始分离。这表明早期层充当“编码器”，负责识别任务，而后期层则负责执行解决方案。

转向真实 LLM: Llama, Gemma 等

合成数据对理论研究很有用，但这在真实的大语言模型中成立吗？作者在从 Llama-3.1-8B 到 Gemma-2-27B 的模型上测试了这一点，使用了自然任务:

  • 词性 (POS) 标注: (例如，“找出名词”) 。
  • 位运算: (例如，逻辑与 AND、或 OR、异或 XOR 运算) 。

测量“任务可解码性”

为了量化模型对任务的理解程度，作者引入了一个名为任务可解码性 (Task Decodability, TD) 的指标。

TD 很简单: 一个简单的分类器 (如 k-最近邻) 能否观察模型的隐藏状态并正确猜出模型正在执行哪个任务 (例如，“名词”还是“动词”) ？

  • 高 TD: 任务在模型的大脑中是分离良好的聚类。
  • 低 TD: 模型感到困惑；表示是重叠的。

图 3. Llama-3.1-8B 中的任务编码。上图: 中间表示的 UMAP。下图: TD 分数。

在图 3中，看看名词 (Noun) (红色) 和介词 (Preposition) (紫色) 之间的区别。

  • 名词: 形成一个紧密、独特的聚类。TD 分数很高。
  • 介词: 分散且与“Null”类重叠。TD 分数很低。

至关重要的是，当我们提供更多的“shots” (提示中的示例) 时，TD 分数会上升。上下文示例充当信号，帮助模型聚焦并分离任务聚类。

高 TD 意味着更好的性能吗？

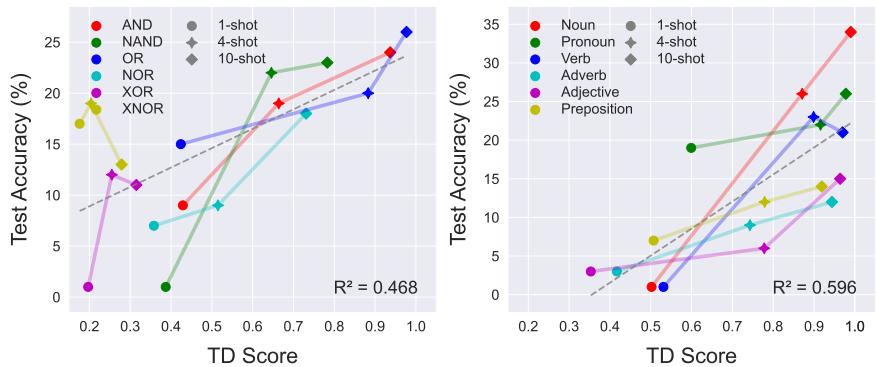
这对从业者来说是最重要的发现。任务被编码的好坏 (TD 分数) 与模型表现的好坏 (准确率) 之间存在近乎线性的关系。

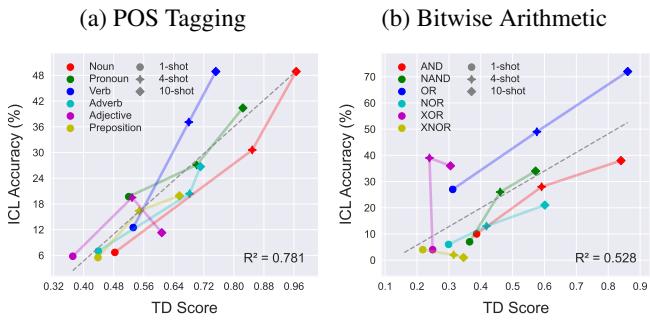
图 4. Llama-3.1 8B 中 TD 分数与 ICL 性能的对比。我们在大多数任务中观察到正相关趋势。

如图 4所示，如果 TD 分数高，模型几乎肯定会有高准确率。如果 TD 分数低，模型就会失败。这表明 ICL 的瓶颈通常不在于模型做这项任务的能力，而在于它识别你想要它做哪个任务的能力。

这种关系并非 Llama 独有。它在不同的模型家族和规模中都成立，如下面的 Gemma 和 Llama-70B 所示:

图 21. Gemma-2 模型和 Llama-3.1-70B 中 TD 分数与 ICL 性能的对比。

令人惊讶的是，这甚至适用于像 Mamba (RNNs) 这样的非 Transformer 架构，表明这是神经网络从上下文中学习的一个基本属性:

图 22. Mamba-2 8B 模型中 TD 分数与 ICL 性能的对比。

证明因果关系: 我们能“黑入”任务向量吗？

相关性不等于因果性。为了证明这些向量实际上导致模型解决任务，研究人员进行了激活修补 (Activation Patching) 。

他们本质上是在模型试图解决一个任务 (或空任务) 时，“注入”另一个任务 (例如“AND”) 的任务向量。

  • 正向干预 (Positive Intervention) : 注入正确的任务向量应该会提升性能。
  • 负向干预 (Negative Intervention) : 注入错误的任务向量应该会破坏性能。

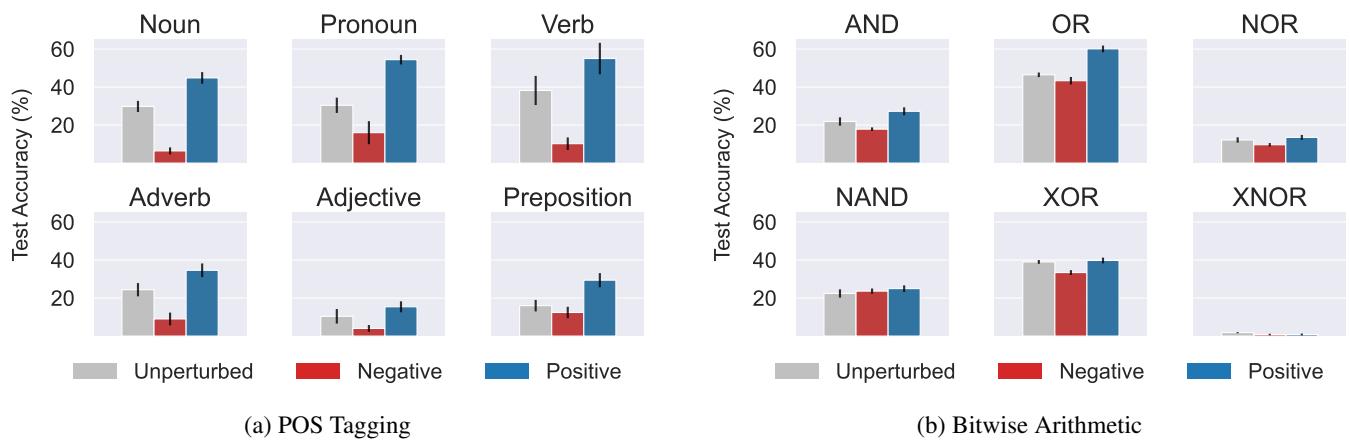
图 20. 通过干预对概念编码进行的因果分析。

图 20 证实了这一点。看右边的位运算 (Bitwise Arithmetic) 图表。

  • 灰色条: 基线性能。
  • 蓝色条 (正向) : 性能跃升 (对于 AND/OR 等任务显着提升) 。
  • 红色条 (负向) : 性能崩溃。

这证实了 ICL 过程确实是由这些几何任务向量介导的。

层解剖: 魔法发生在哪里？

如果模型是一个“编码器-解码器”，边界在哪里？

研究人员绘制了 Llama-3.1 各层的 TD 分数。

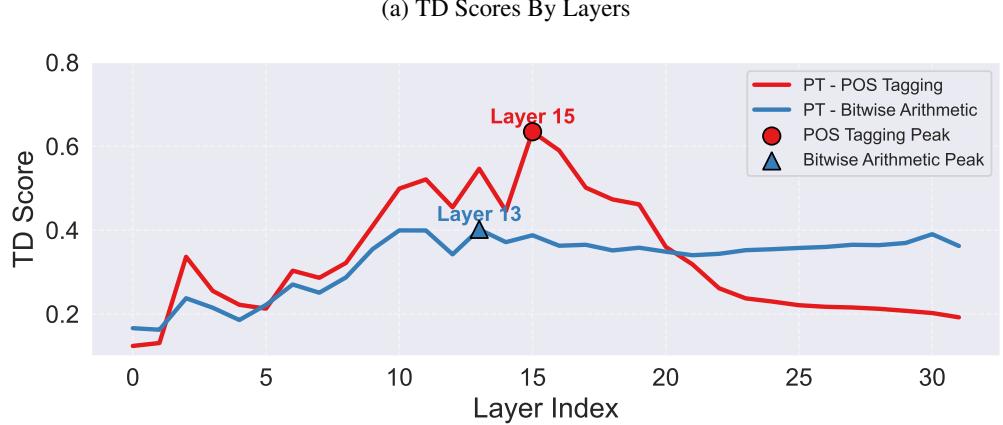
图 19. 各层 TD 分数。

在图 19 (a) 中，注意峰值。识别任务的能力 (TD) 急剧上升并在 13-15 层左右达到峰值，然后下降。

这意味着:

  1. 早期层 (0-15) : 编码器 。 这些层负责消化提示并弄清楚“这是什么任务？”
  2. 后期层 (16+) : 解码器 。 一旦任务被识别，这些层执行特定的算法以生成答案。任务信息被“消耗”或转化为答案，这就是为什么 TD 会下降。

启示: 微调早期层！

这一见解挑战了机器学习中的一个惯例。通常，当我们微调模型 (如使用 LoRA) 时，我们专注于后期层或预测头，假设那是特定知识存在的地方。

但如果瓶颈是任务识别，我们应该修复编码器。

研究人员通过对比微调前 10 层与微调后 10 层来测试这一点。

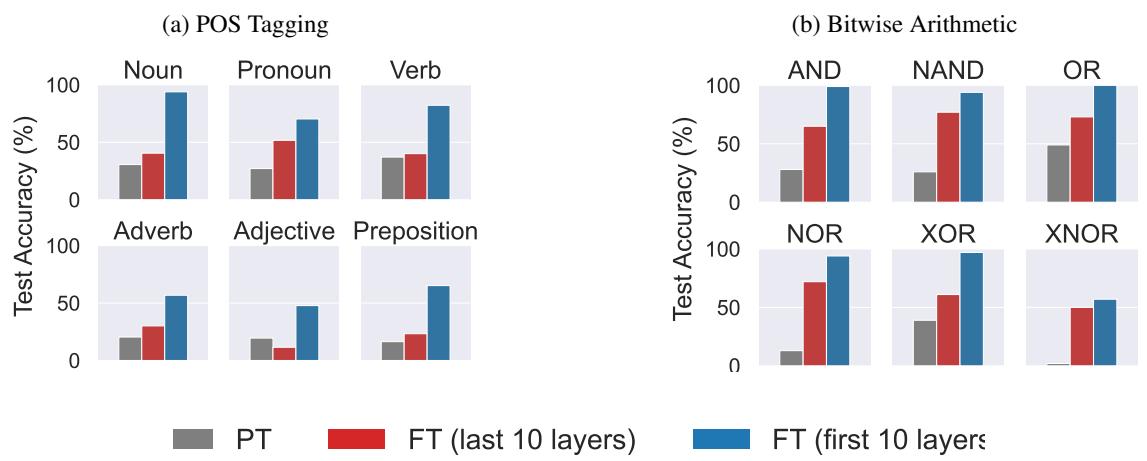
图 24. 微调 (FT) 前 10 层和后 10 层后，POS 和算术中 12 个任务的 4-shot ICL 测试准确率。

图 24 中的结果令人震惊。

  • 蓝色条 (前 10 层) : 巨大的性能提升。
  • 红色条 (后 10 层) : 中等或可忽略的提升。

对于“位运算”，微调前 10 层使准确率从接近零提高到接近 100%。通过帮助模型在早期层清晰地“看到”任务，下游的执行层终于可以完成它们的工作了。

预训练期间的演变

最后，论文提出了一个问题: 这种能力是如何在 LLM 的大规模预训练过程中涌现的？利用 OLMo-7B 模型的检查点，他们追踪了数千个训练步骤中的 TD 和准确率。

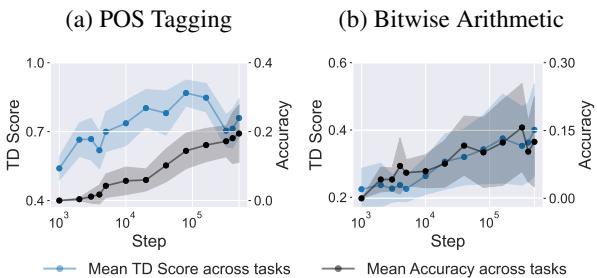
图 5. OLMo-7B 预训练期间的 TD 分数和 ICL 准确率。

如图 5 所示，这两条线几乎完美同步。随着模型学会构建其内部几何结构以分离任务 (TD 分数上升) ，其执行上下文学习的能力也同时涌现。

结论

这项研究为上下文学习的魔法提供了一个令人信服的“机制性”解释。它让我们不再将 LLM 视为“黑盒”，而是将其理解为执行两个不同操作的结构化引擎:

  1. 任务编码: 在早期层将潜在概念分离成不同的几何聚类。
  2. 任务解码: 使用这些特定的聚类在后期层触发算法回路。

给学生和从业者的关键要点:

  • 几何形状具有预测性: 仅仅通过观察任务向量在隐藏状态中的分离程度，你就可以预测模型在该任务上的表现。
  • “编码器”是独特的: Transformer 的早期层承担了弄清楚任务是什么的繁重工作。
  • 微调策略: 如果你的模型难以遵循指令或掌握任务，尝试微调早期层 。 你可能是在修复“任务编码器”而不是执行引擎。

随着我们要继续扩展模型，理解它们为什么有效与让它们工作得更好同样重要。这种“编码器-解码器”视角让我们离完全破译大语言模型的内部语言又近了一步。