引言

大型语言模型 (LLM) 如 Llama 3 和 Qwen2.5 的能力正在以惊人的速度增长。然而，随着这些模型的规模扩展到数千亿参数，运行它们的计算成本——特别是在推理阶段——正变得令人望而却步。推理主要面临两个瓶颈: 计算受限的预填充阶段 (处理你的提示词) 和内存受限的生成阶段 (逐个吐出 token) 。

为了让这些模型能够在标准硬件上运行 (或者仅仅是在数据中心 GPU 上运行得更快) ，我们依赖量化技术——将模型的数值精度从 16 位浮点数 (FP16) 降低到 8 位或 4 位整数。虽然权重的量化已经解决得比较好了，但要将激活值 (流经网络的临时数据) 和 KV 缓存 (模型对对话的记忆) 量化到 4 位而不导致模型输出乱码，仍然是一个巨大的挑战。

为什么？因为离群值 (Outliers) 。 在 LLM 的激活值中，极小部分的数值比其余数值大几个数量级。如果你试图将这些离群值挤进微小的 4 位网格中，你要么得截断它们 (丢失关键信息) ，要么得把网格拉得非常宽，导致那些较小的、包含细节的数值淹没在量化噪声中。

在这篇文章中，我们将深入探讨 ResQ (Residual Quantization，残差量化) ，这是在顶级机器学习会议上提出的一种新方法。它提出了一种数学上最优的方式来处理这些离群值。通过结合混合精度量化与主成分分析 (PCA) , ResQ 达到了最先进的性能，有效地解锁了高精度的 4 位推理。

背景: 对抗离群值之战

在理解 ResQ 之前，我们需要了解当前的量化格局。

问题所在

当我们量化一个矩阵 \(X\) 时，我们将它连续的数值映射到一个离散的整数集。标准公式如下所示:

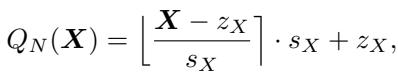
显示舍入和缩放过程的量化公式。

这里，\(s_X\) 是缩放因子。如果矩阵 \(X\) 有一个巨大的离群值 (例如 100) ，而大多数值都在 -1 到 1 之间，那么 \(s_X\) 必须很大以容纳这个 100。结果是，-1 到 1 之间的值可能都会被舍入为 0，从而破坏了信号。

现有的解决方案

研究人员开发了两种主要策略来应对这个问题:

  1. 混合精度 (离群通道检测) : 识别离群值所在的特定通道 (列/行) ，将它们保持在高精度 (如 8 位或 16 位) ，而将其余部分压缩到 4 位。这里的挑战在于: 你如何决定哪些通道是“重要”的？ 大多数方法只是寻找最大值 (\(\ell_{\infty}\)-范数) 。
  2. 旋转 (统一精度) : 将激活矩阵乘以一个随机旋转矩阵。这会将离群值“均摊”到所有通道上，使分布更平滑 (更接近高斯分布) ，从而更容易进行统一量化。

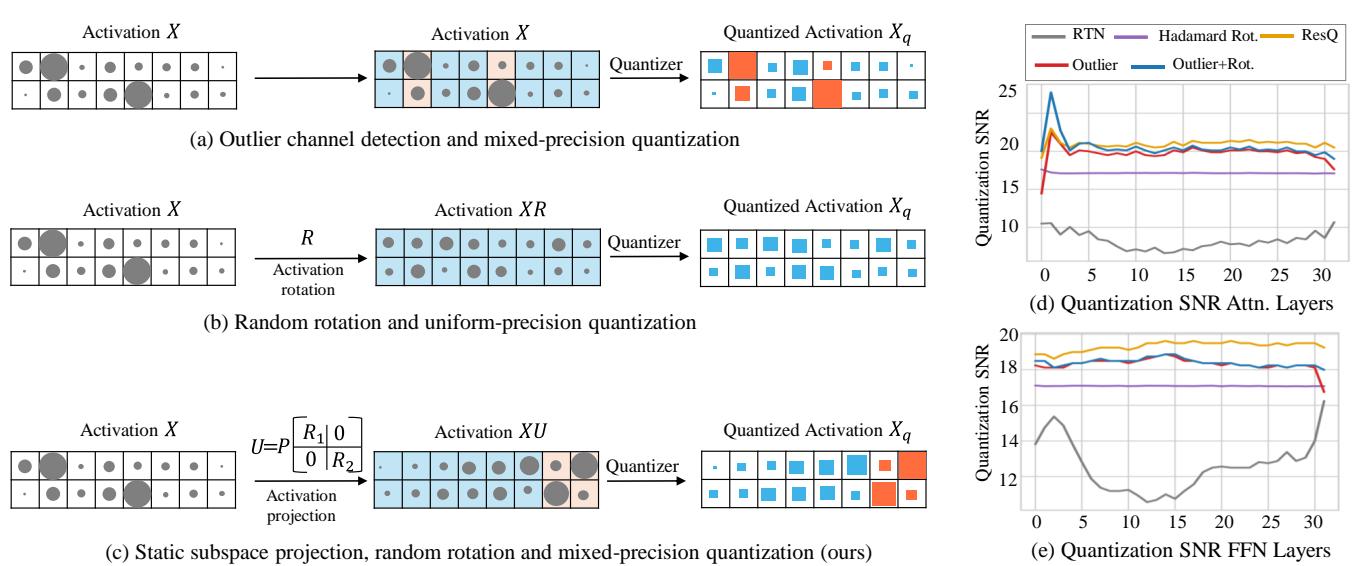
量化方法的比较: (a) 基于离群值的混合精度，(b) 基于旋转的方法，以及 (c) 结合了两者的 ResQ。

如上图 Figure 1 所示，现有的方法通常只选择其中一条路。 (a) 展示了离群值检测，特定的高幅度通道以橙色 (高精度) 保留。 (b) 展示了旋转，数据被打乱以变得均匀。

ResQ (c) 提出了一个问题: 为什么不双管齐下？更具体地说，为什么不使用比单纯的“幅度”更好的指标来决定哪些部分保留高精度？

核心方法: ResQ

ResQ 代表 Residual Quantization (残差量化) 。其核心理念是识别出一个包含最多信息 (方差) 的“低秩子空间”，将其保留在高精度，并将“残差” (其余部分) 降级为低精度。至关重要的是，它在这些子空间内使用了不变随机旋转 , 以进一步平滑数据。

分解

研究人员提出使用正交基 \(U\) 来分解输入激活值 \(X\) 和权重 \(W\)。他们将这个基分为两部分:

  • \(U_h\): 高精度子空间 (秩为 \(r\)) 。
  • \(U_l\): 低精度子空间 (秩为 \(d-r\)) 。

量化后的激活值 \(X_q\) 计算如下:

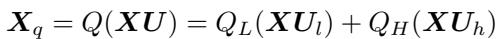
公式显示量化后的 X 被分解为低精度和高精度分量。

这个公式的意思是: 将 \(X\) 投影到低精度空间 (\(X U_l\)) 并进行激进量化 (\(Q_L\)) ，然后将 \(X\) 投影到高精度空间 (\(X U_h\)) 并进行温和量化 (\(Q_H\)) 。将它们相加，就得到了结果。

为什么正交性很重要

你可能会想，“拆分矩阵并进行乘法运算难道不会增加巨大的计算开销吗？”

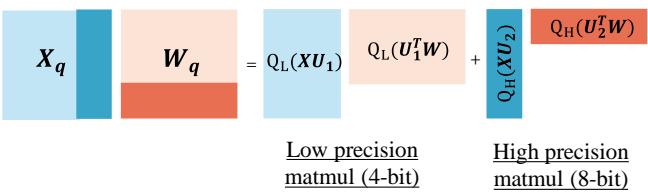
这就是数学优雅的地方。由于基 \(U\) 是正交的，矩阵乘法中的交叉项消失了。当你将量化后的激活值 \(X_q\) 乘以量化后的权重 \(W_q\) 时，运算可以被干净地分解:

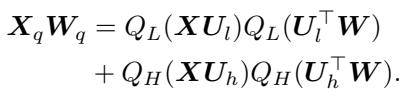
矩阵乘法分解显示交叉项消失，只留下低-低和高-高交互。

这意味着硬件只需要对大部分数据执行 4 位 GEMM (通用矩阵乘法) ，并对少量高精度部分执行 8 位 GEMM。两种精度之间没有混乱的交互。

下方的 Figure 2 展示了这种对硬件友好的流程。注意巨大的蓝色块 (4 位) 和细长的米色块 (8 位) 是如何分别处理，然后简单相加的。

混合精度操作数的矩阵乘法示意图。

秘诀: PCA 与最优性

这篇论文最重要的贡献在于他们如何选择高精度子空间 \(U_h\)。像 QUIK 这样的旧方法基于最大绝对值 (幅度) 来选择通道。ResQ 使用的是 主成分分析 (PCA) 。

作者证明了一个定理 (定理 4.2) ，表明为了最小化量化误差，你不应该寻找最大的值，而应该寻找最大的方差。

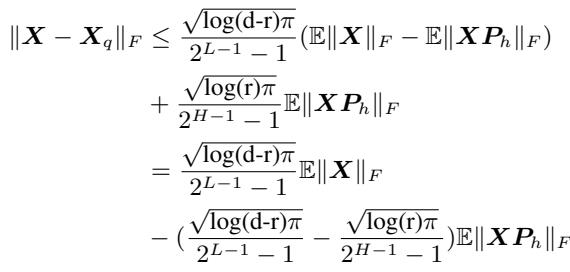
显示量化误差上界的公式。

上面的公式给出了误差的上界。为了使误差 (左侧) 尽可能小，你需要尽可能多地减去右侧的部分。这意味着最大化 \(\|XP_h\|_F\)。在线性代数中，能最大化投影数据 Frobenius 范数的投影 \(P_h\)，正是协方差矩阵 \(XX^T\) 的前几个特征向量。

简单来说: ResQ 运行一个快速的校准步骤 (使用 PCA) 来找到数据中波动最大的“方向”。它将这些方向分配给 8 位精度，而将那些枯燥、静态的方向分配给 4 位。

加入旋转

一旦通过 PCA 确定了子空间，ResQ 会在这些子空间内部应用随机旋转 (\(R_l\) 和 \(R_h\)) 。

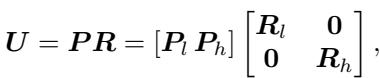
U 矩阵被定义为投影 (P) 和旋转 (R) 的乘积。

这种旋转确保了在 4 位组内没有单一通道是离群值，并且在 8 位组内数据也分布良好。

对分布的影响

这种复杂的数学运算真的改变了数据吗？是的，变化巨大。

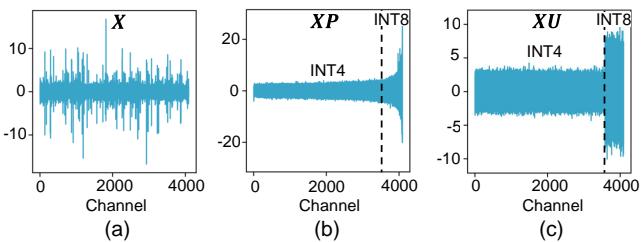
下方的 Figure 3 展示了激活值的分布。

  • (a) 基线是锯齿状且嘈杂的。
  • (b) 应用 PCA (\(XP\)) 后，通道按方差排序。你可以看到右侧 (高方差) 突然升高。
  • (c) 应用 ResQ (\(XU\)，包含旋转) 后，一切都变得平滑。“INT4”部分是平坦的，易于量化；“INT8”部分则承载了主要信息。

图表显示激活分布: 基线 vs. 投影后 vs. ResQ。

在 LLM 模块中的实现

在 Transformer 中实现这一点不仅仅是做一次矩阵乘法那么简单。为了避免降速，投影操作需要在可能的情况下融合到权重中。

作者为模型的不同部分定义了特定的投影矩阵:

  1. \(U_A\): 用于注意力和前馈 (FFN) 模块的输入。
  2. \(U_B, U_C\): 用于 KV 缓存中的 Value 和 Key 头。
  3. \(U_D\): 用于 FFN 中的巨型下投影 (down-projection) 。

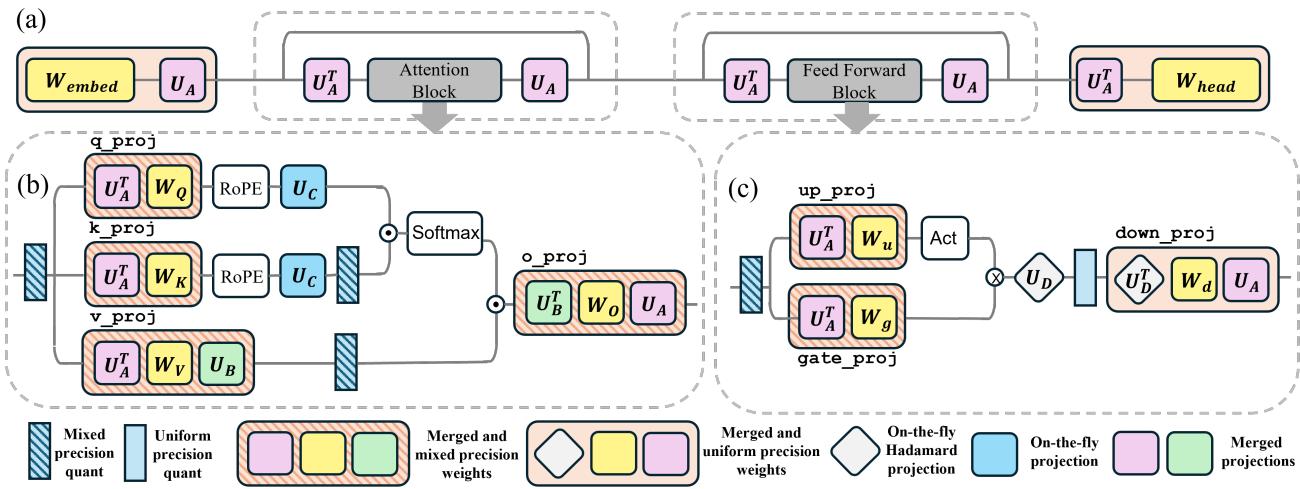
Transformer 模块示意图，显示 U_A, U_B, U_C 和 U_D 的应用位置。

关键工程技巧: 对于作用在 FFN 隐藏层维度 (非常巨大) 上的 \(U_D\)，进行全矩阵乘法太慢了。作者巧妙地选择 \(U_D\) 为一个 Hadamard 矩阵 。 Hadamard 变换可以使用快速专用内核 (快速 Walsh-Hadamard 变换) 计算，使得投影在计算上几乎是免费的。

实验与结果

研究人员在 Llama 2、Llama 3、Llama 3.2 和 Qwen2.5 系列上测试了 ResQ。设置通常是将权重、激活值和 KV 缓存全部量化为 4 位 (W4A4KV4) ，仅保留 1/8 的通道为 8 位。

困惑度和准确率

结果显示，ResQ 明显优于 SpinQuant、QuaRot 和 QUIK 等竞争方法。

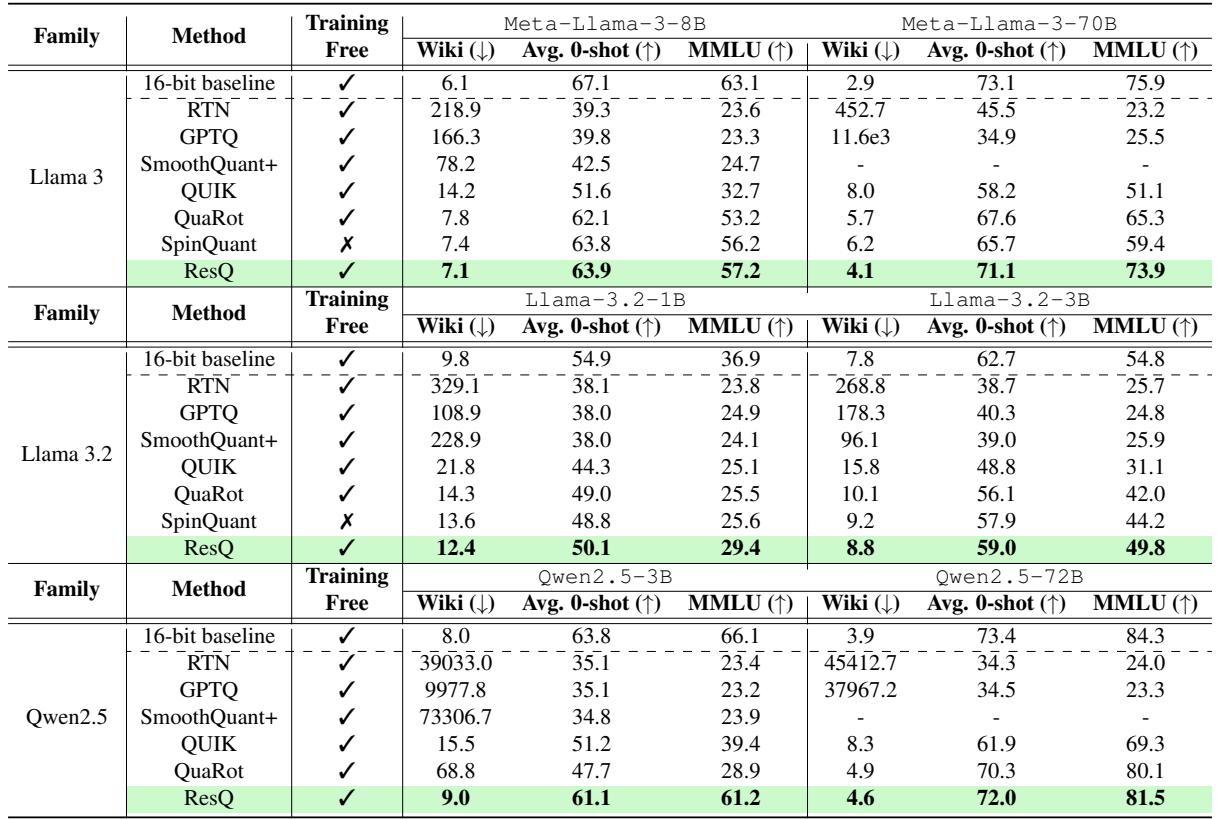
在 Table 1 中，请看 Meta-Llama-3-70B 这一列。

  • RTN (最近舍入) 完全破坏了模型 (困惑度 > 400) 。
  • GPTQ (仅权重) 失败了，因为它没有处理激活值。
  • SpinQuant (之前的 SOTA) 得到了 6.2 的困惑度。
  • ResQ 达到了 4.1 的困惑度 , 显著更接近 16 位基线。

表 1: Llama 模型在困惑度和准确率上的比较。

生成能力

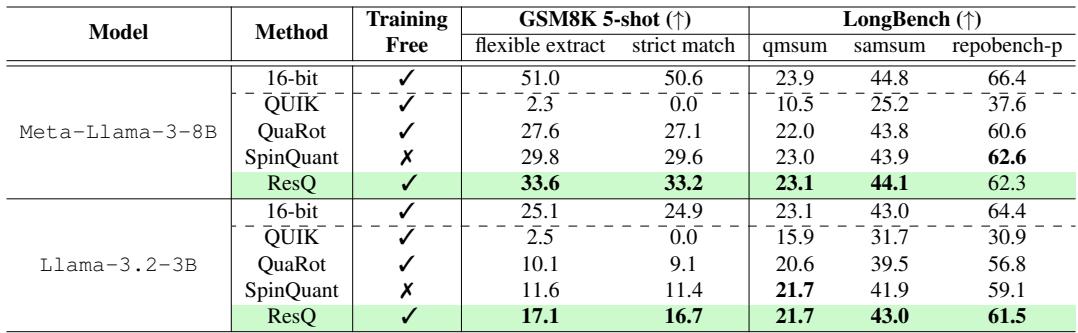
拥有良好的困惑度 (预测下一个词) 是一回事，但模型还能做数学和写代码吗？

Table 2 重点展示了在 GSM8K (数学) 和 HumanEval 类任务 (代码) 上的表现。对于 Llama-3-8B , ResQ 在 GSM8K 上得分 33.6% , 击败了 SpinQuant 的 29.8% 和 QUIK 的 2.3% (QUIK 在这里完全崩溃了) 。这证实了 ResQ 比其他 4 位技术更好地保留了模型的“推理”能力。

表 2: 在 GSM8K 和 LongBench 等生成任务上的表现。

可视化改进效果

为了直观地理解 为什么 ResQ 效果更好，我们可以查看信噪比 (SNR) 和实际的激活值。

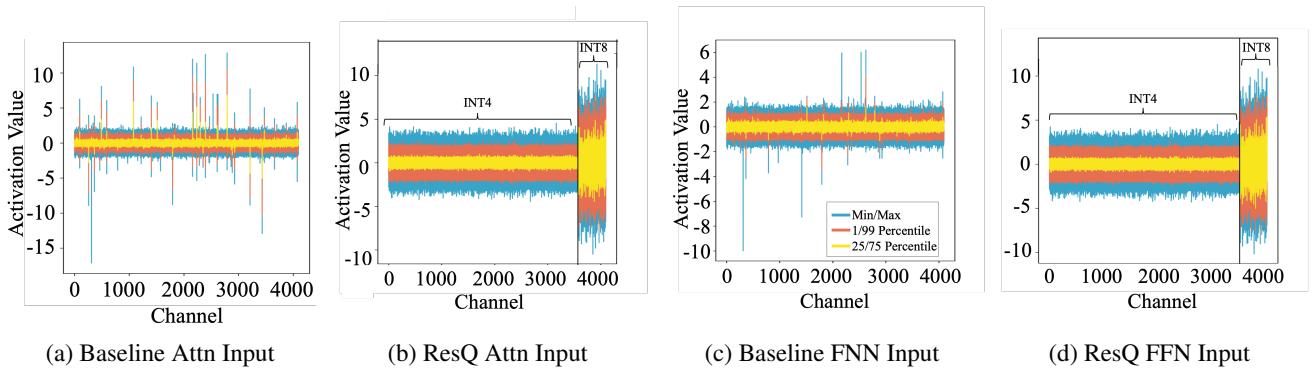
Figure 7 比较了输入激活值。

  • 上图 (基线) : 数值在 -15 到 +10 之间剧烈波动。
  • 下图 (ResQ) : 数值被严格控制，大部分停留在 -5 到 +5 之间。这个紧凑的范围对 4 位量化要“友好”得多。

注意力和 FFN 层的输入激活分布比较。

加速比

最后，“训练后量化” (PTQ) 的承诺是速度。ResQ 做到了吗？

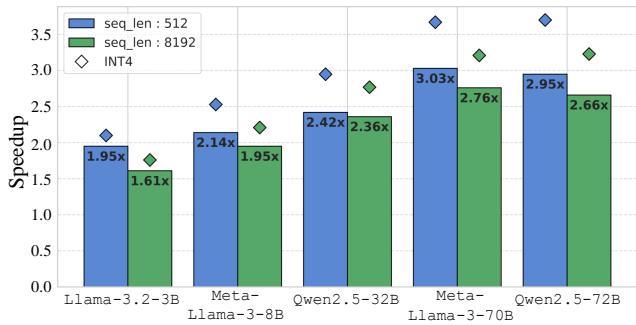
在 NVIDIA RTX 3090 上，ResQ 相比 16 位基线实现了高达 3 倍的加速 。 关键是，它仅比纯朴素的 INT4 内核慢约 14%。这意味着混合精度处理 (拆分矩阵) 和即时投影的开销，与减少内存带宽带来的收益相比是微不足道的。

条形图显示 ResQ 在 RTX 3090 上的加速比。

结论与启示

ResQ 代表了 LLM 量化领域的成熟。我们已经超越了简单的舍入 (RTN) 和静态离群值截断。我们正在进入一个量化能够“感知”数据结构的时代。

通过使用 PCA 在数学上将高方差的“信号”与低方差的“噪声”分离，ResQ 允许我们将“比特预算”花在最重要的地方。

核心要点:

  1. 不要只看幅度: 对于混合精度来说，方差 (PCA) 是比单纯的绝对值更好的重要性指标。
  2. 正交性很高效: 将矩阵分解为正交子空间允许在不进行复杂交叉计算的情况下实现混合精度。
  3. 旋转辅助量化: 即使在找到最佳子空间后，随机旋转也有助于平滑剩余的离群值。
  4. 4 位 W/A/KV 是可行的: 我们正在缩小与 16 位性能的差距，这使得在消费级硬件或更便宜的云实例上运行像 Llama-3-70B 这样的巨型模型成为可能。

随着 LLM 的不断增长，像 ResQ 这样优化推理阶段的技术，很可能会成为模型部署流程中的标准组件。