超越准确率——何时我们该停止改进算法，转而扩大准入范围？

在数据科学和公共政策领域，普遍存在一种假设: 更好的模型会带来更好的结果。我们花费无数时间调整超参数、收集更多特征，并不懈追求 AUC 或 \(R^2\) 那 0.01 的提升。这种逻辑听起来很有道理——如果我们能更准确地预测谁面临贫困、失业或辍学的风险，我们就能更有效地进行定向帮扶。

但是，如果瓶颈不在算法上呢？如果帮助那些处境最不利者的最佳方式不是更智能的 AI，而仅仅是增加预算以帮助更多的人呢？

这正是研究论文 “The Value of Prediction in Identifying the Worst-Off” (预测在识别最弱势群体中的价值) 所提出的核心问题。研究人员引入了一个严谨的框架来比较两种截然不同的政策杠杆: 改进预测与扩大准入 (筛选能力) ，从而挑战了对预测准确率的盲目追求。

通过理论建模和针对德国失业问题的海量真实案例研究，他们揭示了一个反直觉的真相: 在许多实际场景中，投资于“更聪明”的系统所带来的回报，往往不如简单地扩大覆盖范围。

问题: 资源受限环境下的分配

想象一下，你是一名负责社会项目的政策制定者。你的预算有限，只能为一小部分人口提供密集支持——比如说风险最高的前 10%。你的目标是识别出“处境最不利者” (例如，那些最有可能面临长期失业的人) 并进行干预。

你有两个主要手段可以调节以改进这个系统:

1. 改进预测: 投资于更好的数据和复杂的机器学习模型，以便更准确地对个人进行排名。
2. 扩大准入: 投资于更多的个案工作者或资源，以增加你可以筛选和帮助的人数 (例如，从帮助前 10% 增加到前 12%) 。

当前实证公共政策的趋势严重倾向于第一种选择。机构专注于风险评分的增量改进。然而，这些改进是有成本的——数据基础设施、技术债务和不透明性。这篇论文提供了缺失的框架，用于确定哪种投资实际上能提供更多的“价值”。

框架: 预测 vs. 准入

为了在数学上权衡这种取舍，作者定义了一个特定的问题设定。我们要面对一群人，他们有真实的福利结果 \(Y\) (例如未来的收入或就业时长) 。我们要识别出处境最不利的那部分人口 \(\beta\)。

然而，我们无法预知 \(Y\)。我们只有一个预测器 \(f(x) = \hat{Y}\)。 我们还有一个资源约束 \(\alpha\)，这是我们能够负担得起去筛选或治疗的人口比例。

系统的 价值 (Value) 被定义为我们成功筛选出真正属于处境最不利群体的概率。

在这里，\(t(\alpha)\) 和 \(t(\beta)\) 分别是筛选能力和目标高风险群体的阈值。简单来说就是: 在真正需要帮助的人中，我们的系统成功捕获了多大比例？

预测-准入比率 (PAR)

这就引出了这篇论文的核心贡献: 一个被称为 预测-准入比率 (Prediction-Access Ratio, PAR) 的新指标。这个指标告诉我们，与改进预测相比，扩大准入的相对“性价比”如何。

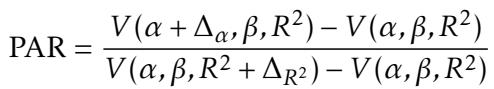
PAR 将小幅增加容量带来的边际价值收益 (\(\Delta_\alpha\)) 与小幅增加预测准确率带来的边际价值收益 (\(\Delta_{R^2}\)) 进行比较。

• 如果 PAR > 1: 扩大准入更有效。通过帮助稍多一点的人获得的价值，比让模型稍微变聪明一点获得的价值更多。
• 如果 PAR < 1: 改进预测更有效。你应该专注于数据质量和建模。

要做出一项经济决策，你只需将 PAR 与这些改进的相对成本进行比较。

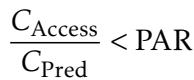
如果准入成本与预测成本的比率小于 PAR，你就应该购买更多的准入名额。

理论洞察: 高斯模型

为了建立直觉，作者首先使用简化的“玩具模型”来分析这个问题，其中结果和误差服从正态 (高斯) 分布。在这个纯净的数学世界中，预测器的质量完全由决定系数 \(R^2\) 捕获。

将策略可视化有助于我们理解其中的权衡。

在上方的 图 1 中，我们可以看到三种情况:

• (a) 左图: 基线。黑色曲线显示了给定真实结果 \(Y\) 时被筛选出来的概率。注意它不是一个完美的阶跃函数——一些需要帮助的人 (垂直线左侧) 被漏掉了，而一些不需要帮助的人被选中了。
• (b) 中图: 扩大准入 (\(\alpha\))。曲线向上移动。我们捕获了更多处境最不利者，仅仅是因为我们总体上筛选了更多的人。
• (c) 右图: 改进预测 (\(R^2\))。曲线变得更陡峭。系统区分需要帮助者和不需要帮助者的能力变强了，将概率质量向左移动。

问题是: 哪个阴影区域 (价值的增益) 更大？

预测的“第一公里和最后一公里”

最引人注目的理论结果之一是作者所谓的 “第一公里和最后一公里” 效应。

他们发现，在两种极端状态下，改进预测最有价值:

1. 第一公里: 当你几乎一无所知时 (\(R^2 \approx 0\))。从随机猜测转变为基本模型会有巨大的帮助。
2. 最后一公里: 当你已经非常准确，且你的能力与目标群体规模相匹配时 (\(\alpha \approx \beta\))。在这里，优化模型有助于完美分配。

然而，在混乱的“中间地带”——大多数现实世界系统运行的地方——扩大准入往往是赢家。

图 2 可视化了不同容量 (\(\alpha\)) 和准确率 (\(R^2\)) 下的 PAR。

• 红色/橙色区域 表示 PAR 很高 (>1)。这意味着扩大准入是主导策略。
• 注意左侧大片的红色区域。论文中的 定理 3.1 证明，当筛选能力稀缺 (\(\alpha\) 很小) 时，扩大准入的价值是压倒性的。如果你只能帮助 1% 的人，将其翻倍至 2% 的影响力远大于微调你的模型。
• 蓝色区域 (PAR < 1) 主要出现在预测极差 (底部) 或近乎完美 (右上角) 的时候。

结论是什么？除非你的模型是全新的或者是近乎完美的，否则你很可能处于运营能力比算法复杂性更重要的区域。

真实案例研究: 德国的长期失业问题

理论界限很有用，但在现实世界的复杂性中是否成立？为了找出答案，研究人员将他们的框架应用于来自德国联邦就业局的海量行政数据集。

任务: 预测长期失业 (Long-Term Unemployment, LTU)。 数据: 2010 年至 2017 年求职者、就业历史和福利的记录。 目标: 识别“处境最不利者”——定义为将失业超过 12 个月的人 (大约占人口的 15%，所以 \(\beta \approx 0.15\)) 。

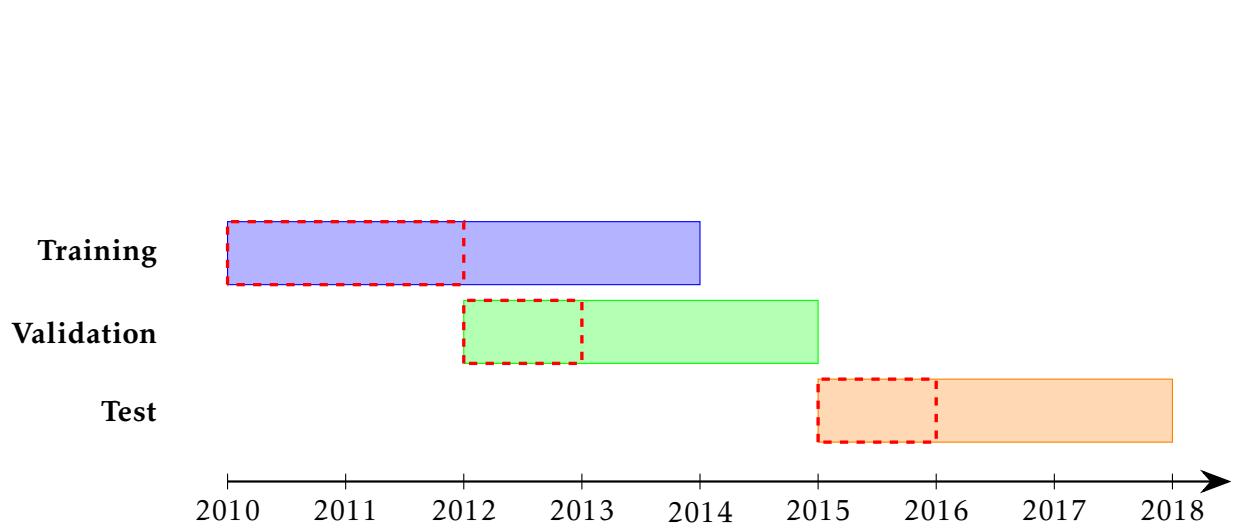
他们训练了一个梯度提升模型 (CatBoost) 来预测失业时长。该模型实现了大约 0.15 的 \(R^2\)。这听起来可能很低，但在人类行为高度不可预测的复杂社会结果预测中，这是标准水平。

结果 1: 准入的主导地位

实证结果几乎完美地反映了理论。

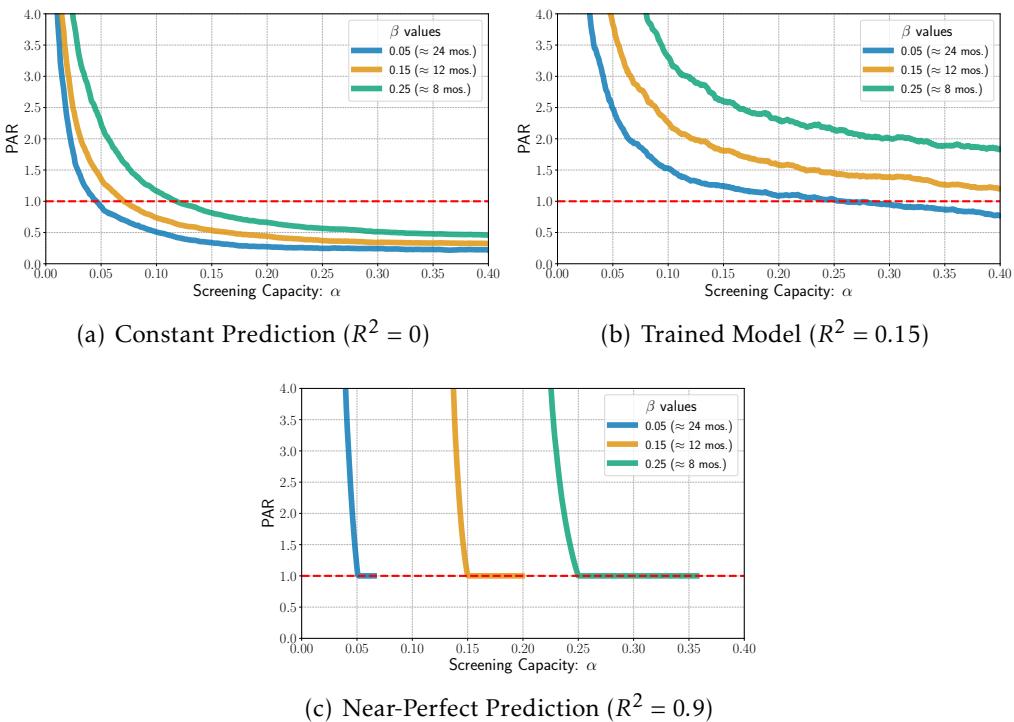
图 6 显示了基于真实测试数据计算出的 PAR。请看橙色线 (代表 12 个月的失业目标) 。在很宽的筛选能力范围内，PAR 始终高于 1.0 (红色虚线) 。

这证实了对于典型的社会预测系统 (\(R^2\) 适中) ，多筛选一个人的边际价值高于同等模型准确率提升的边际价值。

结果 2: 简单模型 vs. 复杂模型

政府面临的一个常见两难选择是: 使用透明、简单的模型 (如决策树或检查表) ，还是“黑盒”AI (如神经网络或梯度提升) 。黑盒通常更准确，但更难解释和维护。

作者对比了一个简单的 4 层决策树 和复杂的 CatBoost 模型。

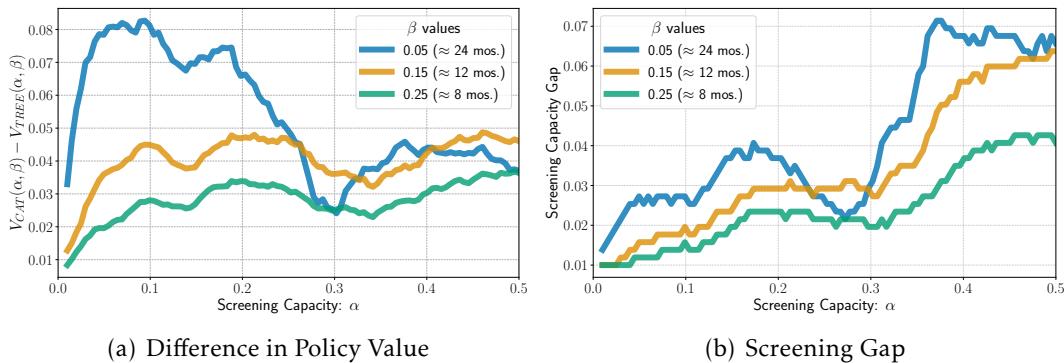
• 图 (a) 显示了政策价值的差异。复杂模型 (CatBoost) 确实更好 。 它识别出了更多处境最不利者。
• 图 (b) 改变了游戏规则。它提出了一个问题: 我们需要给决策树系统增加多少额外的能力，才能使其达到与 CatBoost 系统相同的性能？

答案出奇的小——通常只需增加 0.05 到 0.07 的筛选能力。

这为复杂性提供了一个具体的“价格标签”。政策制定者可以看着这个数据问: “构建、托管和解释一个复杂的 AI 系统更便宜，还是简单地雇佣足够的员工多筛选 5% 的人并使用简单的检查表更便宜？” 通常，后者不仅更便宜，而且更稳健、更透明。

结论: 别忘了“准入”这个杠杆

AI 在公共政策中的诱惑在于“优化”的承诺——用同样的资源做更多的事。这篇论文给这种优化热泼了一盆冷水。它提醒我们，预测是达到目的的手段，而不是目的本身。

给学生和从业者的关键启示:

1. 背景为王: 你不能仅凭准确率指标 (如 MSE 或 AUC) 来评估模型的价值。你必须在分配问题的背景下评估它: 我们试图寻找谁？我们能帮助多少人？
2. 稀缺陷阱: 如果你的项目规模很小 (低 \(\alpha\)) ，与扩大项目规模相比，改进模型的回报微不足道。
3. 中间地带: 在社会科学预测典型的“混乱中间地带” (\(R^2\) 在 0.15 到 0.50 之间) ，扩大准入通常是更优的政策手段。
4. 复杂性是有代价的: 在部署最先进的模型之前，计算一下“等效准入”。你是否可以通过使用更简单的模型并略微增加预算来获得相同的福利结果？

通过计算 预测-准入比率 (PAR) , 我们可以将对话从“我们要如何构建更好的模型？”转变为“我们要如何构建更好的系统？”——一个平衡预测的智慧与扩大准入的关怀的系统。