深度学习有一个迷人且稍微反直觉的特性: 如果你在相同的数据上训练两个相同的神经网络架构，它们将学会同样出色地完成任务，但它们的内部权重看起来会完全不同。

这种现象给 模型融合 (Model Fusion) 带来了巨大的挑战——模型融合是指在不访问原始训练数据的情况下，将多个已训练的模型合并为一个单一、更优模型的技术。如果你简单地对两个不同模型的权重进行平均 (这是联邦学习或模型集成中常用的技术) ，结果通常是一个性能低下的“损坏”模型。为什么？因为这些模型虽然在功能上相似，但在参数空间中并没有 对齐 (Aligned) 。

多年来，研究人员一直试图通过利用 置换对称性 (Permutation Symmetry) 来解决这个问题。他们对一个模型的神经元进行重新排序 (置换) ，使其与另一个模型相匹配。这对于像 MLP 或 CNN 这样的标准网络效果很好。然而，正如我们在这篇文章中将要探讨的，置换的刚性本质不足以应对 Transformer 复杂的高维几何结构。

在这篇对论文 “Beyond the Permutation Symmetry of Transformers: The Role of Rotation for Model Fusion” 的详细解读中，我们将探索一种开创性的方法，即从离散的置换转向连续的 旋转对称性 (Rotation Symmetry) 。 我们将看到在注意力机制内部旋转矩阵如何实现 Transformer 模型的理论最优对齐，从而显著改善模型融合的效果。

对称性问题

要理解旋转，我们首先需要理解当前标准的局限性: 置换。

MLP 中的置换

考虑一个简单的多层感知机 (MLP) 。网络由通过权重连接的层级神经元组成。如果你交换第 \(l\) 层中两个神经元的位置，然后交换第 \(l+1\) 层中相应的输入权重，网络的输出将保持完全不变。

在数学上，一个 MLP 层可以描述为:

MLP 层方程。

这里，\(\sigma\) 是一个逐元素的激活函数 (如 ReLU) 。这里的“对称性”由一个置换矩阵 \(P\) 定义。如果我们对权重应用置换 \(P\)，函数保持不变，因为我们可以对下一层应用逆置换。

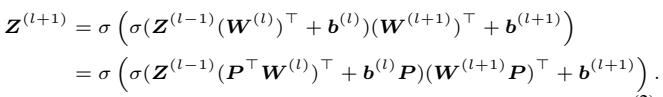
显示 P 被抵消的置换对称性方程。

这里的关键点是，对于 MLP 来说，“等价集 (equivalence set) ”——即产生完全相同函数的所有权重配置的集合——是由这些离散的交换定义的。

Transformer 的挑战

Transformer 的构造不同。虽然它们包含表现得像 MLP 的前馈网络 (FFN) ，但它们的核心力量来自于 自注意力层 (Self-Attention Layers) 。

在 FFN 中，逐元素的激活函数 (如 ReLU) 限制了我们要么只能交换神经元，因为任何其他线性变换都会被非线性激活破坏。

然而，自注意力依赖于非线性 (Softmax) 应用 之前 的线性矩阵乘积 (Query 乘以 Key) 。这种结构上的差异开启了更广泛的对称性类别的大门。本文作者认为，如果仅局限于交换行和列 (置换) ，我们就忽略了注意力机制连续的几何本质。

引入旋转对称性

这篇论文的核心贡献是 旋转对称性 在 Transformer 中的形式化。

与其仅仅交换索引，如果我们能旋转参数空间的整个坐标系会怎样？

注意力的几何学

让我们看看自注意力层的数学原理。注意力分数是通过 Query 矩阵 (\(X_Q\)) 和 Key 矩阵 (\(X_K\)) 相乘计算得出的。

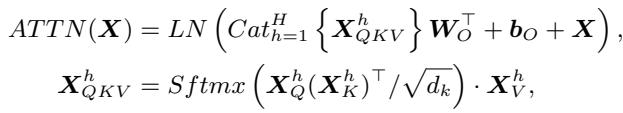
标准注意力机制公式。

现在，考虑一个旋转矩阵 \(R\)。旋转矩阵是正交的，意味着如果将其与它的转置相乘，你会得到单位矩阵 (\(RR^\top = I\)) 。

作者意识到我们可以将这个单位矩阵插入到注意力方程中而不改变结果。我们可以用 \(R\) 旋转 Queries，并用 \(R^\top\) “反向旋转” Keys。

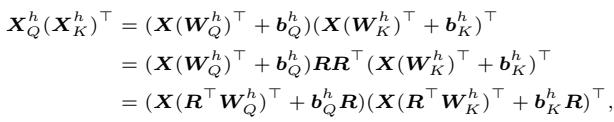
推导过程展示插入 R 和 R 的转置如何保持 Query-Key 乘积不变。

如上所示，内积保持完全相同。即使权重矩阵 \(W_Q\) 和 \(W_K\) 已经发生了变换，模型计算出的注意力分数也是完全一样的。

同样的逻辑也适用于 Value (\(V\)) 和 Output (\(O\)) 矩阵。我们可以旋转 Values 并反向旋转 Output 投影。

架构可视化

这为我们提供了一套新的规则，可以在不改变 Transformer 功能的情况下变换其权重。

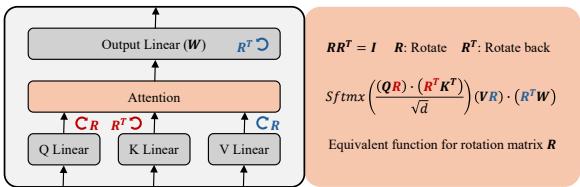
图 1. 自注意力层的旋转对称性。

如图 1 所示:

  1. Q-K 对: 我们对 Query 权重和 Key 权重应用旋转 \(R_{qk}^\top\)。因为其中一个在注意力操作中被转置，它们相互抵消。
  2. V-O 对: 我们对 Value 权重应用旋转 \(R_{vo}^\top\)，并对 Output 权重应用 \(R_{vo}\)。

这一发现意义重大，因为旋转是在 连续空间 中操作的。与离散的置换 (你要么交换神经元 1 和 2，要么不交换) 不同，旋转允许对模型参数的对齐进行平滑、无限的调整。

算法: 最优参数匹配

这为什么重要？因为 模型融合 (Model Fusion) 。

当我们想要合并两个模型 (比如模型 A 和模型 B) 时，我们通常会对它们的参数进行加权平均。然而，神经网络的损失地形 (loss landscape) 是非凸的。即使模型 A 和模型 B 都在低损失的解上，它们之间的“直线”平均通常会穿过一个高损失区域 (即“损失壁垒”) 。

我们需要在平均之前将模型 A 匹配 (match) (对齐) 到模型 B。我们希望找到一个旋转 \(R\)，使模型 A 的权重在数学上尽可能接近模型 B 的权重，同时不改变模型 A 的实际预测结果。

直觉

图 2 使用损失地形等高线图很好地展示了这一概念。

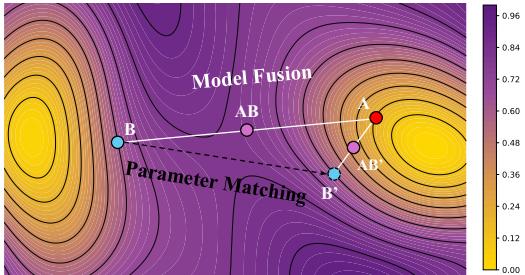
图 2. 参数匹配在损失地形上的直观示例。

  • A 和 B 是我们的原始模型。
  • AB 代表简单的合并。它落在一个高损失 (黄色/绿色) 区域。
  • AB’ 代表 参数匹配 后的合并。通过旋转模型 A 以与模型 B 对齐，合并后的模型落在一个深层的低损失盆地 (紫色) 中。

匹配的数学原理

作者将这种对齐公式化为一个优化问题。对于前馈网络 (FFN) ，由于 ReLU 激活函数的存在，他们仍然使用置换匹配。

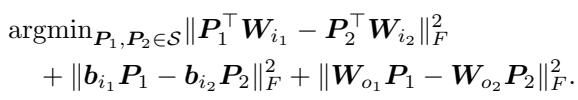
FFN 置换匹配的优化问题。

然而，对于注意力层，他们使用了新的旋转对称性。目标是最小化源模型 (1) 和锚点模型 (2) 权重之间的欧几里得距离 (Frobenius 范数) 。

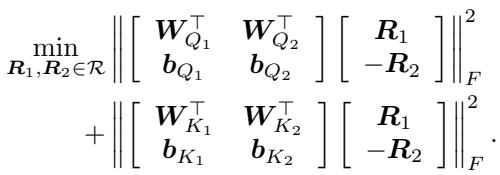
注意力旋转匹配的优化问题。

这看起来像是一个复杂的回归问题，但由于 \(R\) 被约束为正交旋转矩阵，这属于一类已知的问题，称为 正交普洛克路斯忒斯问题 (Orthogonal Procrustes Problem) 。

闭式解

值得注意的是，我们不需要梯度下降来找到最佳旋转。作者提供了一个定理，表明利用奇异值分解 (SVD) 存在一个闭式解。

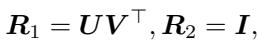
使用 SVD 的闭式解。

最优旋转 \(R\) 简单地等于 \(UV^\top\)，其中 \(U\) 和 \(V\) 来自权重矩阵乘积的 SVD。这使得匹配算法在计算上非常高效且数值稳定。

添加重缩放

作者更进一步。除了旋转，神经网络还表现出 重缩放对称性 (Rescaling Symmetry) (例如，将权重乘以 \(\alpha\) 并将下一层除以 \(\alpha\)) 。他们将其整合到算法中，求解一个标量 \(a\) 以进一步最小化距离。

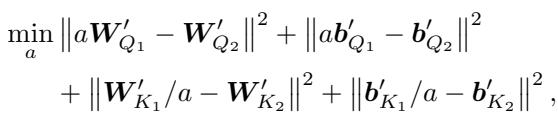
包含标量重缩放的优化问题。

实验结果

理论很完善，但实际效果如何？作者在不同领域测试了他们基于旋转的匹配算法。

自然语言处理 (NLP)

他们在情感分类和命名实体识别 (NER) 任务上微调了 RoBERTa 和 DeBERTa 模型。然后，他们使用三种不同的融合技术合并成对的模型:

  1. Simple: 直接平均。
  2. Fisher: 基于 Fisher 信息的加权平均。
  3. RegMean: 基于回归的合并。

在所有情况下，他们将基线融合与 + 匹配 (本文方法) 后的融合进行了比较。

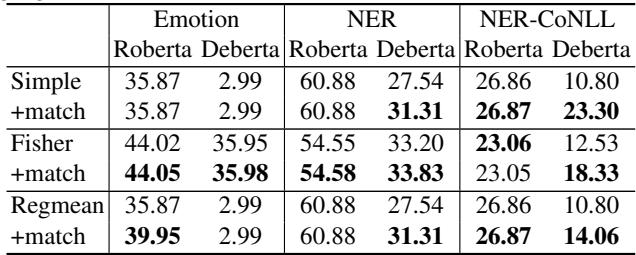
表 1. NLP 任务的实验结果。

表 1 的关键要点:

  • 一致的提升: +match 行几乎普遍优于基线。
  • 简单融合的显著改善: 看看 DeBERTa / Emotion 这一列。简单融合完全失败了 (准确率: 2.99) ，很可能是因为模型未对齐。经过匹配后，它跳回到了可用的性能水平。
  • 最先进水平 (SOTA) : 即使对于像 RegMean 这样的高级方法，添加旋转匹配也能挤出额外的性能。

计算机视觉

他们还在图像分类任务 (CIFAR-10) 上测试了视觉 Transformer (ViT) 。他们将旋转方法与最优传输 (OT) 基线进行了比较。

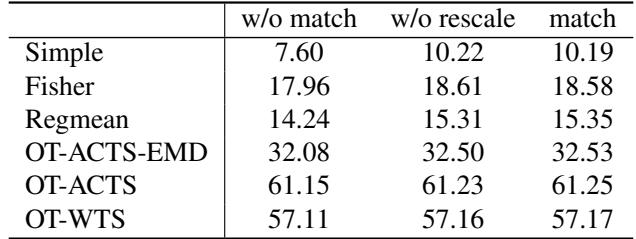
表 2. ViT 在图像分类上的实验结果。

表 2 中的结果加强了 NLP 的发现。基于旋转的匹配 (最右列) 始终产生最高的准确率。

消融实验: 什么最重要？

是注意力层中的旋转还是 FFN 中的置换对成功贡献最大？

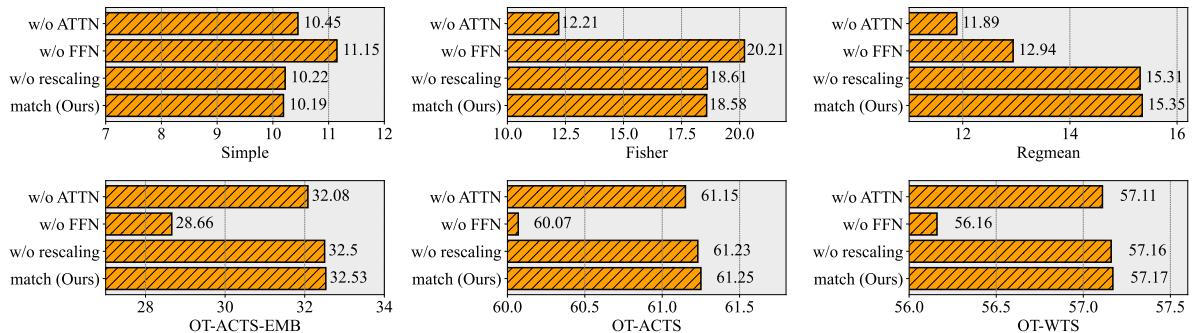
图 3. 比较无注意力匹配与无 FFN 匹配的消融研究。

图 3 揭示了一个有趣的细节。

  • 对于 Fisher 和 RegMean 合并，移除注意力匹配 (w/o ATTN，紫色条) 会导致性能显著下降。这证明了对齐连续的注意力空间对于这些高级合并方法至关重要。
  • 对于 OT-Fusion , FFN 匹配似乎更占主导地位，但本文的完整方法 (橙色条) 在所有情况下仍然是最好或并列最好的。

损失壁垒

为了从物理上证明模型在优化地形中“更接近”，作者绘制了模型 A 和模型 B 路径之间的损失。

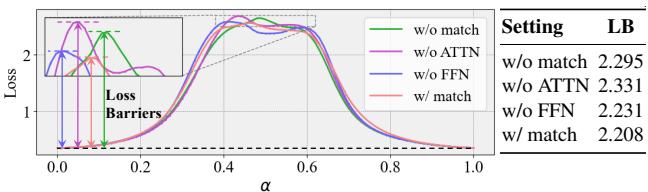
图 5. 显示壁垒降低的损失地形。

在图 5 中，绿线 (无匹配) 显示在模型之间移动时损失出现巨大的尖峰 (“壁垒”) 。红线 (匹配) 几乎是平坦的。这种“线性模式连通性 (Linear Mode Connectivity) ”是模型融合的圣杯——它意味着这两个模型实际上位于损失地形的同一个凸盆地中。

计算复杂度

有人可能会担心对每一层执行 SVD 会很慢。

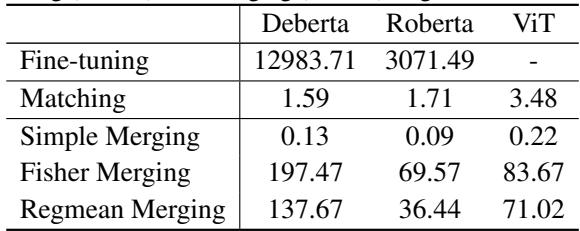
表 3. 运行时间分析。

表 3 消除了这些疑虑。匹配过程大约需要 1.5 到 3.5 秒——与微调模型所花费的小时数相比，这几乎可以忽略不计。这是一个高效的“即插即用”模块。

讨论: 效率与深度

作者调查了最后一个问题: 我们需要匹配每一层吗?

他们在使用 24 层 DeBERTa 模型的实验中，尝试只匹配特定的层子集。

图 6. 匹配层子集时的评估损失。

图 6(a) 显示了匹配 单个 层的影响。有趣的是，匹配较早的层 (索引 0-5) 比匹配较晚的层更能降低损失。

图 6(b) 证实了这一趋势。“尾部层匹配 (Tail-Layers Matching) ”曲线表明，匹配最后几层提供的好处非常少。只有当包含早期层 (“头部”层) 时，损失的下降 (改善) 才会加速。这表明 Transformer 的早期层在训练期间发散得更厉害，最需要对齐。

结论

这项研究标志着我们对 Transformer 几何结构的理解迈出了重要一步。通过将 旋转对称性 确定为置换对称性的连续推广，作者解锁了一种更强大的模型对齐方法。

关键要点:

  1. Transformer 是连续的: 将对齐限制在离散的置换上忽略了自注意力矩阵的几何性质。
  2. 旋转是最优的: 我们可以使用闭式解 (Procrustes/SVD) 来求解最佳对齐，而不是用离散求解器进行近似。
  3. 更好的融合: 通过旋转对齐模型可以大幅降低它们之间的损失壁垒，使得在朴素方法失败的情况下也能成功合并。
  4. 高效: 该算法快速、可扩展，并且可以作为现有融合技术的即插即用增强模块。

随着我们要迈向去中心化 AI 和联邦学习的未来，像这样能够将不同的模型缝合成一个连贯整体的技术，将变得越来越重要。

本文的完整代码可在 https://github.com/zhengzaiyi/RotationSymmetry 获取。