时间序列预测是人类试图解决的最古老的数学问题之一。从古代文明预测作物周期到现代算法在微秒间进行股票交易，目标始终如一: 利用过去来预测未来。然而，时间序列数据本质上是非确定性 (non-deterministic) 的。无论你有多少历史数据，未来永远不会是一个单一的、固定的点——它是一个可能性的分布。

近年来，大型语言模型 (LLM) 的成功促使研究人员将时间序列预测视为一个语言问题。如果我们可以预测句子中的下一个单词，难道我们不能预测序列中的下一个值吗？虽然这种方法已经取得了一些成果，但它从根本上迫使连续数据 (如温度或股票价格) 转变为离散的“token” (就像字典中的单词) 。这种转换往往导致精度的损失和上下文的缺失。

Sundial 应运而生，这是清华大学研究人员在 2025 年的一篇论文中介绍的一个新的时间序列基础模型家族。Sundial 提议摆脱离散的 token 化和僵化的参数假设。相反，它将时间序列视为原生的连续信号，并使用生成式建模 (generative modeling) ——特别是流匹配 (Flow Matching) ——来预测可能的未来。

在这篇文章中，我们将解构 Sundial。我们将探讨为什么当前的基础模型在处理连续数据时表现挣扎，Sundial 的“TimeFlow”机制是如何工作的，并查看实证证据，说明为什么这可能代表了预测领域的新技术前沿。

基础模型格局: 离散 vs. 连续

要理解 Sundial 为何重要，我们首先需要梳理当前时间序列基础模型 (TSFMs) 的格局。如下图所示，现有方法通常分为两类，而 Sundial 开辟了第三类:

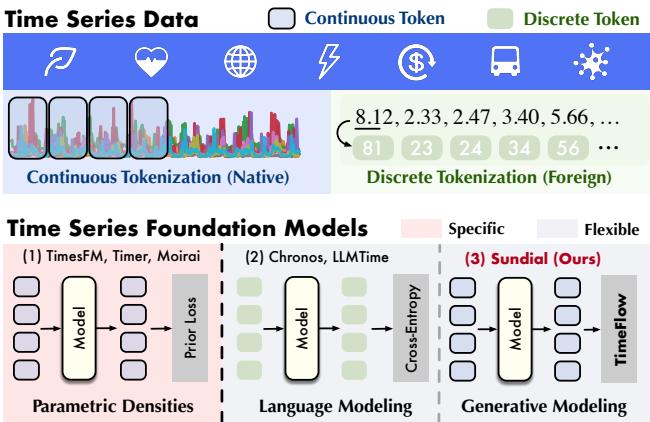
Figure 1: 时间序列基础模型的分类。

1. 参数化密度 (例如 TimesFM, Moirai)

这些模型在连续数据上运行，但假设输出遵循特定的概率分布 (如高斯分布或学生 t-分布) 。模型试图预测该分布的参数 (例如均值和方差) 。

  • 问题: 现实世界的数据是混乱且异质的。通过将预测强加于预定义的数学形状，这些模型通常会遭受“模式坍塌 (mode collapse) ”，即它们倾向于预测平均值，而无法捕捉复杂的多峰可能性。

2. 语言建模 (例如 Chronos, LLMTime)

这些模型将时间序列像文本一样处理。它们将数据离散化 (例如，将值 2.33 转换为 token ID #23) 。

  • 问题: 时间序列值具有数学关系 (2.33 接近 2.34) 。当你把它们变成离散的 token 时，你就失去了这种序数关系。此外，词汇表大小成为了瓶颈，并且量化过程中会丢失精度。

3. 生成式建模 (Sundial)

Sundial 引入了一种“原生”且“灵活”的方法。它保持输入数据连续 (不进行离散化) ，也不假设固定的输出分布。相反，它使用一种称为 TimeFlow 的技术，从头开始学习生成下一块 (patch) 数据的分布。

Sundial 架构

Sundial 不仅仅是一个标准的 Transformer；它是一个为处理时间序列数据的特殊性而设计的系统。让我们看看整体架构。

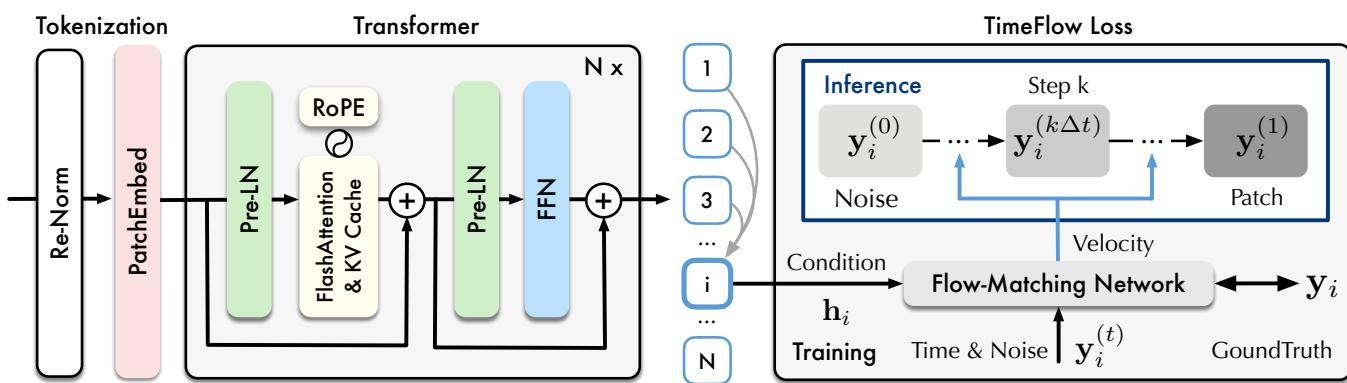
Figure 2: Sundial 的架构。

工作流程包含三个不同的阶段:

  1. Token 化 (Patching) : Sundial 不是逐点处理数据，而是将时间步聚合为“patch (补丁/块) ”。这捕捉了局部语义信息并减少了序列长度，使 Transformer 更高效。至关重要的是，这些 patch 是直接从其连续值嵌入的——不涉及量化。
  2. Transformer 骨干网络: 嵌入被输入到一个仅解码器 (decoder-only) 的 Transformer 中。作者采用了对扩展至关重要的现代优化技术:
  • RMSNorm & Pre-LN: 用于训练稳定性。
  • RoPE (旋转位置嵌入) : 为了更好地捕捉时间上的相对位置。
  • FlashAttention & KV Cache: 显著加快训练速度并降低推理内存使用。
  1. TimeFlow Loss: 这是模型的生成头，我们将在下一节详细介绍。

处理任意长度

基础模型的一个主要挑战是处理具有不同频率和长度的多样化数据集。Sundial 通过 重归一化 (Re-Normalization) 解决了这个问题。在处理之前，输入序列被归一化以减轻分布偏移 (非平稳性) 。然后，patch 嵌入层通过填充和掩码处理任意长度，确保模型可以消化从短期的天气模式到长期的金融历史记录等任何数据。

对于 patch \(\mathbf{x}_i\) 和二进制掩码 \(\mathbf{m}_i\) (指示填充) 的嵌入过程定义为:

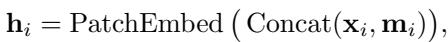
Equation 9: Patch 嵌入公式。

核心创新: TimeFlow Loss

Sundial 技术上最有趣的地方在于它如何学习预测未来。作者提出了基于流匹配 (Flow Matching) 概念的 TimeFlow Loss 。

什么是流匹配？

像扩散模型 (Diffusion Models) 这样的生成模型通过缓慢地向图像 (或数据) 添加噪声直到变成纯噪声，然后学习逆转该过程来工作。流匹配是一个更新、更高效的框架，它在简单的源分布 (如随机高斯噪声) 和复杂的目标分布 (实际数据) 之间创建一条直接的“路径” (或流) 。

想象一个代表随机噪声的粒子场。我们想要推动这些粒子，使它们重新排列成看起来像我们的目标数据。“速度场 (velocity field) ”描述了每个粒子在任何给定时间 \(t\) 需要以什么方向和速度移动才能到达目的地。

其基础数学依赖于一个常微分方程 (ODE) :

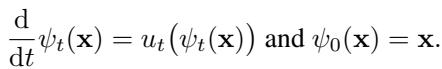
Equation 2: 控制流的 ODE。

这里，\(\psi_t\) 是数据在时间 \(t\) 的位置，\(u_t\) 是速度场。

用于预测的条件流匹配

在时间序列预测中，我们不仅仅是在生成随机数据；我们是在生成以过去为条件的未来。Sundial 训练一个网络来预测以 Transformer 学习到的历史表示为条件的速度场。

目标是最小化网络预测的速度 (\(u_t^{\theta}\)) 与将噪声转换为真实数据 (\(\mathbf{y}_i\)) 所需的理想速度之间的差异。

通用的条件流匹配 (CFM) 损失定义为:

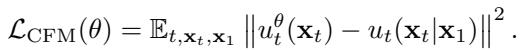
Equation 4: 条件流匹配损失。

通过采用高斯源和“最优传输 (Optimal Transport) ”路径 (噪声和数据之间最直、最高效的路径) ，这在数学上得到了简化。以历史表示 \(\mathbf{h}_i\) 为条件的 Sundial 训练目标变为:

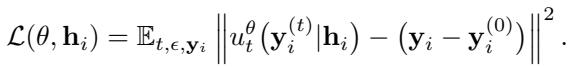
Equation 12: Sundial 损失函数。

这个神经网络被称为 FM-Net (流匹配网络) ，它接受三个输入:

  1. 当前步骤 \(t\) 的噪声数据。
  2. 时间步 \(t\) 本身。
  3. 历史表示 \(\mathbf{h}_i\) (来自 Transformer) 。

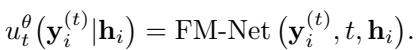
Equation 13: FM-Net 定义。

推理: 生成未来

训练完成后，Sundial 如何预测未来？它执行生成式预测 。

  1. 它从标准高斯分布中采样一个随机噪声向量 \(\mathbf{x}_0\)。
  2. 它使用训练好的 FM-Net 计算离散步骤的速度 (使用 ODE 求解器) 。
  3. 它迭代地更新噪声向量，有效地将其沿着流“推动”，直到它转变为预测的未来 patch。

时间步 \(\Delta t\) 的更新步骤如下所示:

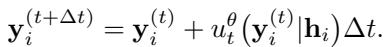
Equation 15: 推理更新步骤。

因为起点是随机噪声，多次运行此过程会生成多个不同的可能预测 。 这使得 Sundial 能够自然地量化不确定性，而无需假设不确定性看起来像钟形曲线。

构建 TimeBench: 万亿级数据集

基础模型的好坏取决于它的数据。为了训练 Sundial，研究人员策划了 TimeBench , 这是一个包含超过 1 万亿个时间点的庞大存储库。

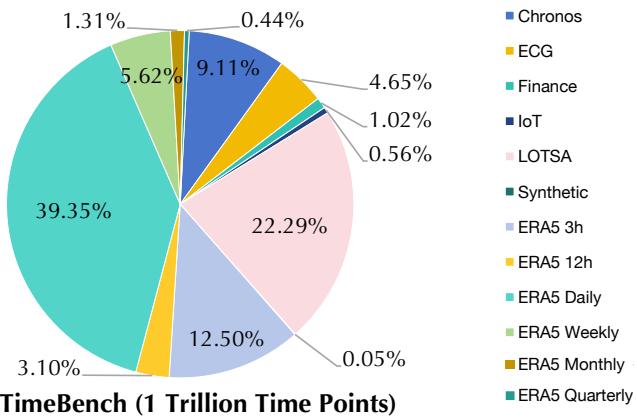
Figure 3: TimeBench 中的数据源。

如上图所示，数据高度多样化:

  • 现实世界数据: 金融、物联网传感器日志、心电图 (ECG) 和海量气象数据集 (ERA5) 。
  • 合成数据: 添加了一小部分 (1.31%) 的合成核，以增强模式的多样性和鲁棒性。

这种规模在时间序列工作中是前所未有的。表 4 (下) 详细列出了具体计数，显示 Sundial 的训练语料库使 Chronos (940 亿点) 或 Lag-Llama 等以前使用的模型相形见绌。

Table 4: TimeBench 统计数据。

实验结果

作者将 Sundial 与该领域目前的重量级模型进行了评估对比: Time-MoE, Timer, Moirai, Chronos, 和 TimesFM。他们在标准基准 (TSLib) 和概率基准 (GIFT-Eval, FEV) 上进行了测试。

1. 点预测 (零样本)

在 Time-Series-Library (TSLib) 基准测试中，Sundial 在“零样本 (zero-shot) ”设置下进行了测试——这意味着它从未在这些特定数据集上进行过训练。

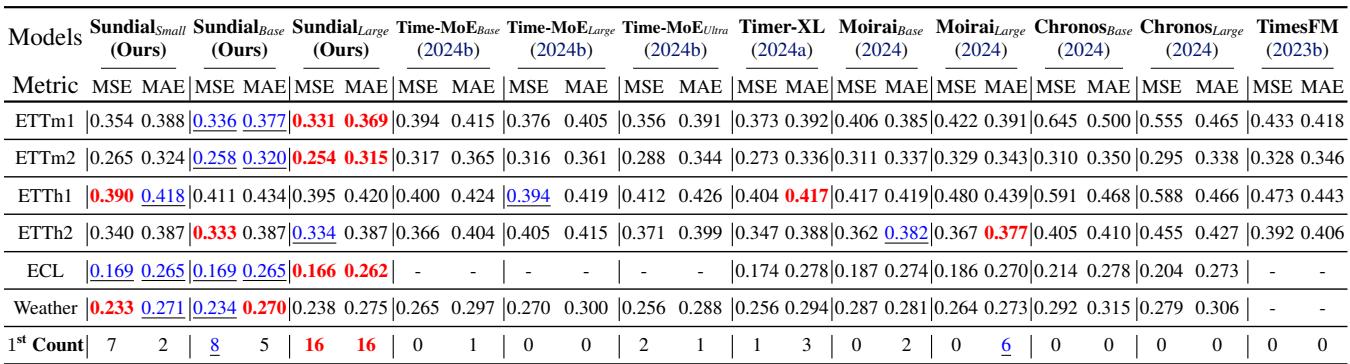
Table 1: TSLib 上的零样本预测结果。

Sundial 在天气和电力 (ECL) 等数据集上始终保持最低的误差 (MSE 和 MAE) 。值得注意的是，它优于 Time-MoE , 这是一个参数量大得多的模型 (24 亿 vs Sundial 的 4.44 亿) ，突显了生成式 TimeFlow 方法相对于单纯参数扩展的效率。

2. 概率预测

这是 Sundial 生成特性的亮点所在。通过采样多个潜在的未来，Sundial 可以估计预测的概率分布。

在 GIFT-Eval 基准 (23 个多样化数据集) 上评估时，Sundial 在 CRPS (连续排名概率评分) 方面取得了顶尖的性能，该指标衡量预测分布与现实的匹配程度。

Table 2: GIFT-Eval 上的概率预测结果。

同样，在 FEV 排行榜上，Sundial 在基础模型中名列前茅。它在取得这些成果的同时，保持了一个关键优势: 速度。

3. 推理速度

生成模型 (如扩散模型) 通常以慢著称，因为它们需要迭代去噪步骤。然而，流匹配通常比扩散更快，因为从噪声到数据的“路径”更直。

作者对 Sundial 进行了优化，使其具有实用性。如图 5 所示，Sundial 的推理速度比基于 LLM 的方法 (LLMTime) 快几个数量级，并且与专门的任务特定模型相比仍具有竞争力。

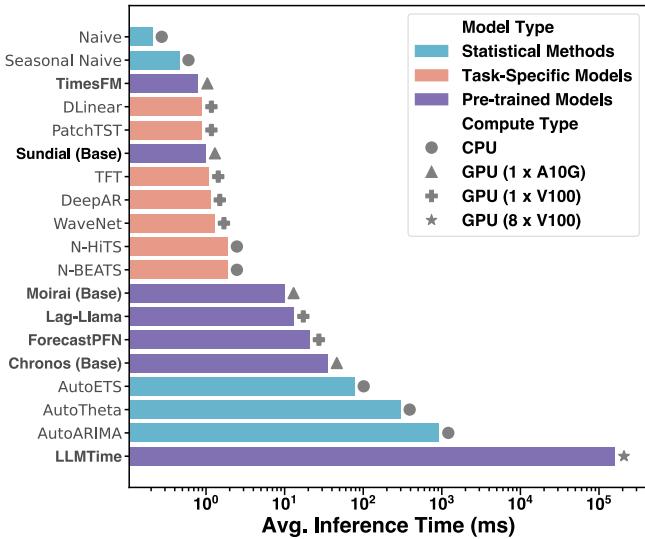
Figure 5: 推理时间评估。

4. 生成能力 vs. 回归

为什么要费力使用流匹配而不是仅仅使用标准的均方误差 (MSE) 损失？答案在于 模式坍塌 (Mode Collapse) 。

当模型最小化 MSE 时，为了稳妥起见，它倾向于预测所有可能未来的平均值。这导致了“模糊”、过于平滑的预测，丢失了时间序列的自然波动性。

图 14 中的对比令人震惊。左侧显示 Sundial (TimeFlow)，右侧显示使用 MSE 训练的相同架构。

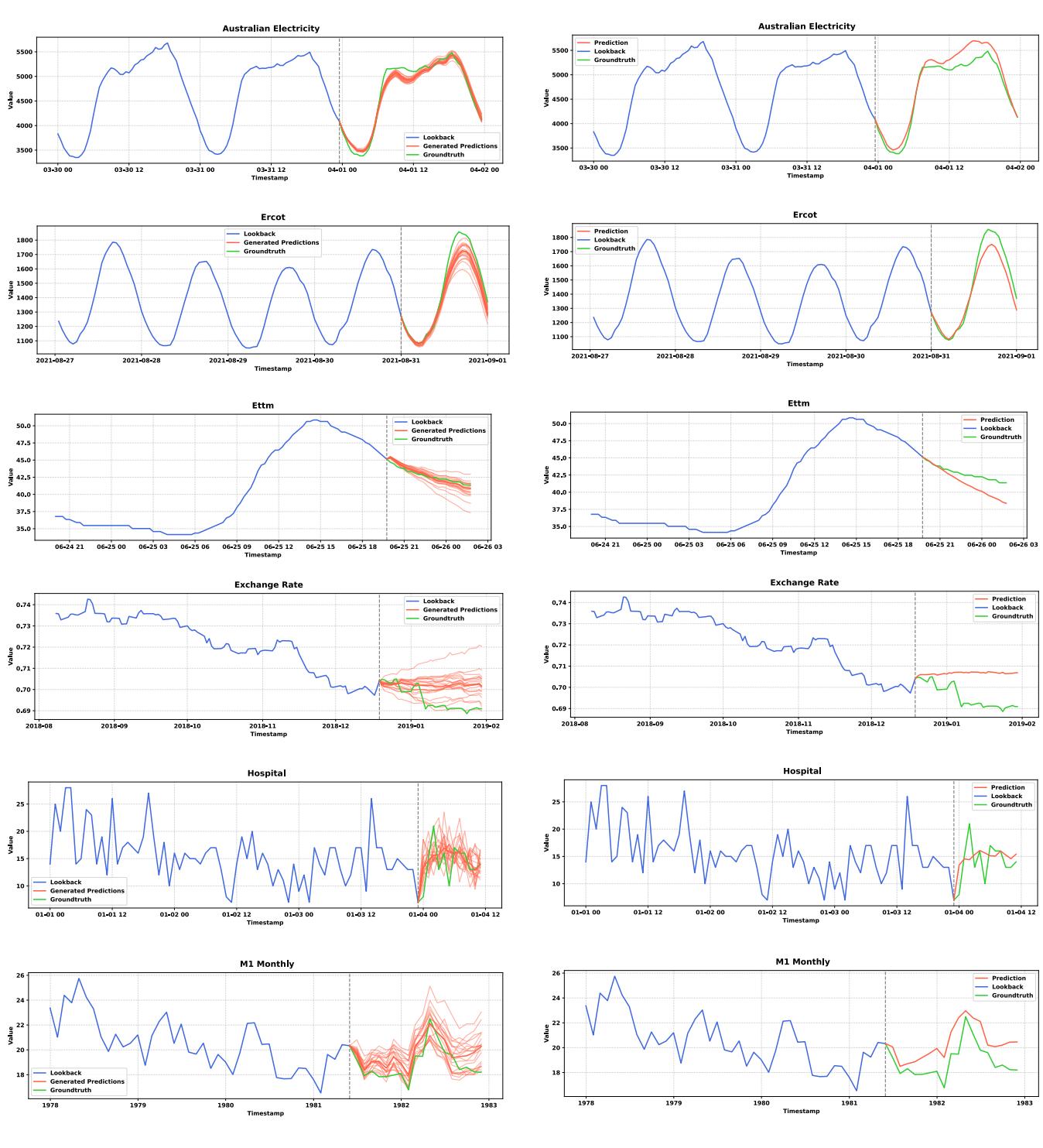
Figure 14: Sundial (左) vs. MSE 训练的模型 (右)。注意右侧过于平滑的预测。

请注意，MSE 预测 (右侧) 通常会收敛成一条平滑的直线 (均值) ，完全无法捕捉真实数据的锯齿状、振荡性质。Sundial (左侧) 生成了清晰、多变的预测，类似于数据的实际动态。

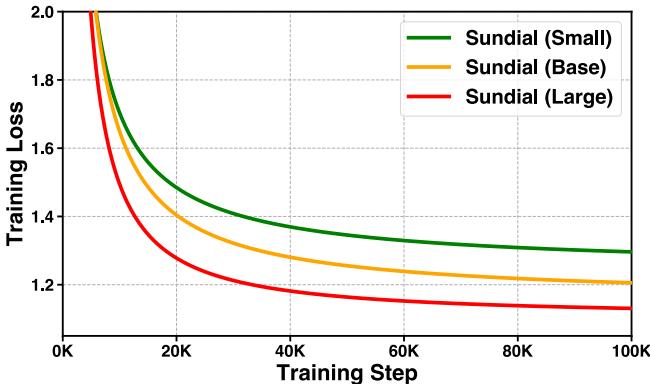
可扩展性和消融实验

该模型是否遵循缩放定律 (scaling laws) ？作者训练了小型 (32M) 、基础型 (128M) 和大型 (444M) 版本。训练曲线表明，仅仅增加模型大小就能带来更好的收敛和更低的损失，这表明我们尚未触及 TimeFlow 能力的天花板。

Figure 6: 显示缩放行为的训练曲线。

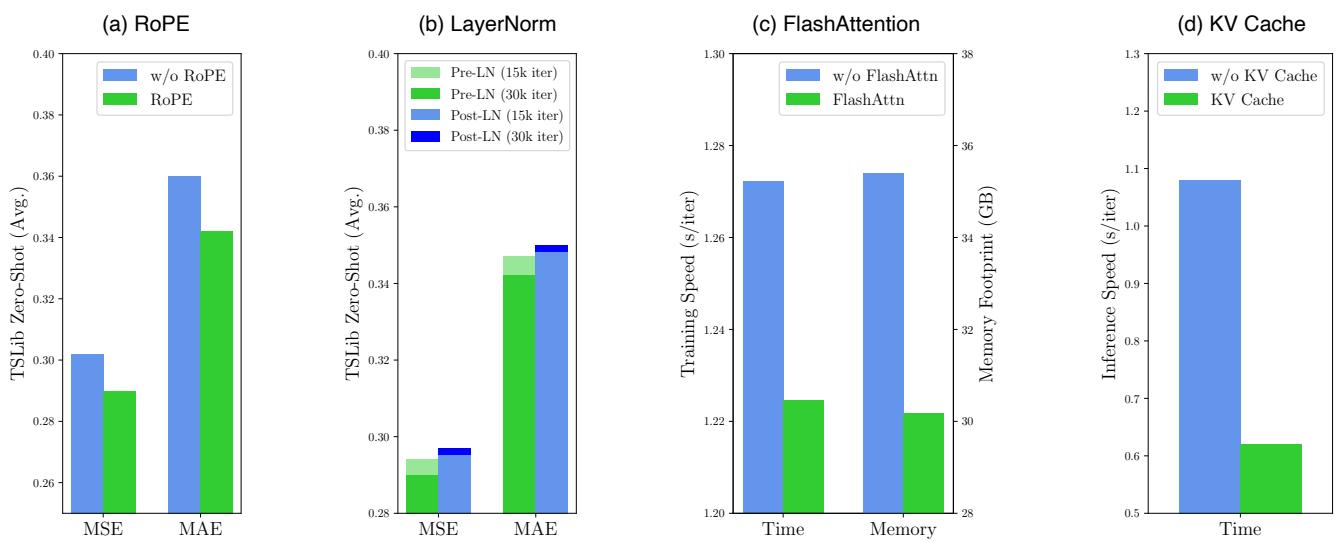
此外，消融研究证实了架构选择——特别是 RoPE 和 Pre-LN——对性能至关重要。有趣的是, FlashAttention 和 KV Cache 提供了巨大的加速 (减少了约 43% 的推理时间) ，而没有牺牲任何准确性。

Figure 9: 关于架构组件的消融研究。

结论

Sundial 代表了时间序列基础模型的“第三次浪潮”。通过拒绝语言模型的离散 token 化和统计深度学习的僵化参数假设，它提供了一种 原生的、灵活的替代方案 。

TimeFlow Loss (条件流匹配) 与海量、多样化的数据集( TimeBench )相结合，使 Sundial 能够捕捉未来固有的不确定性，而不会掩盖细节。它不仅提供预测，还提供可能未来的分布，使其成为不可预测环境中可靠决策的强大工具。

随着基础模型的不断发展，Sundial 证明了将连续数据视为连续数据——而不是强迫它说一种并非为其设计的语言——是一条值得追随的道路。