在机器学习的世界里，预测很少是最终目标。我们进行预测是为了采取行动 。 医生预测诊断结果是为了选择治疗方案；自动驾驶汽车预测行人的移动是为了转向；金融算法预测市场趋势是为了进行交易。

在低风险环境中，比如推荐电影，最大化预期效用是可以接受的。如果模型错了，用户只是浪费了两小时看了一部烂片——这虽然遗憾，但并非灾难性的。然而，在医学或机器人技术等高风险领域，错误的代价是不对称的。仅仅依赖“最可能”的结果可能是危险的。如果一个模型有 90% 的把握认为肿瘤是良性的，基于这个概率采取行动可能会最大化预期效用，但它忽略了那 10% 恶性可能带来的灾难性风险。

这就引出了一个基本问题: 当我们是风险厌恶型时，我们如何将不确定的预测与决策相结合?

在最近的一篇论文中，来自宾夕法尼亚大学的研究人员提出了一个严谨的框架，将不确定性量化与决策理论联系起来。他们介绍了风险厌恶校准 (Risk-Averse Calibration, RAC) , 这是一种证明了预测集 (潜在标签的集合，而非单点预测) 在数学上对风险厌恶型代理是最优的方法。

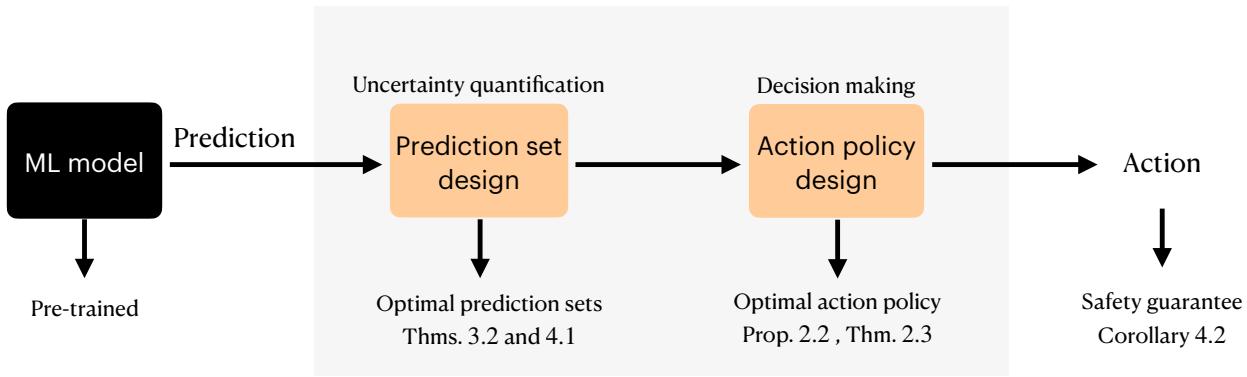
RAC 流程图: 面向高风险应用的预测与行动之间的接口。

如图 1 所示，目标是从原始的机器学习 (ML) 模型过渡到提供安全保证的最佳行动策略。这篇文章将剖析这项工作的决策理论基础，解释为什么预测集是表达风险厌恶的正确语言，并详细介绍 RAC 算法。

问题所在: 风险中性 vs. 风险厌恶

要理解这篇论文的贡献，我们首先需要定义场景。我们有:

  • 特征 (\(X\)): 输入数据 (例如，胸部 X 光片) 。
  • 标签 (\(Y\)): 真实结果 (例如，“肺炎”) 。
  • 行动 (\(A\)): 决策者可用的选择 (例如，“开抗生素”、“送回家”、“进一步检测”) 。
  • 效用 (\(u(a, y)\)): 一个函数，用于评分在真实标签为 \(y\) 的情况下采取行动 \(a\) 有多好。

风险中性代理

标准的机器学习方法通常假设代理是风险中性的。它们依赖于校准 (calibration) , 即模型输出一个概率向量 \(\hat{p}\)。如果一个模型是完美校准的，最优策略是选择最大化预期效用的行动:

\[ a^* = \text{argmax}_{a \in A} \mathbb{E}_{y \sim \hat{p}}[u(a, y)] \]

这在平均情况下效果很好。然而，当“最坏情况”不可接受时，“平均情况”是不够的。

风险厌恶代理

风险厌恶代理不仅仅关心平均值；他们关心的是风险价值 (Value at Risk, VaR) 。 他们想要一个保证。具体来说，他们希望找到一个效用证书 \(\nu(X)\)——即一个有保证的最低效用值——使得:

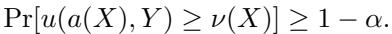
概率不等式显示效用大于或等于 nu 的概率为 1 减去 alpha。

简单来说: “以 \(1 - \alpha\) (例如 95%) 的概率，我保证我的行动效用至少为 \(\nu(X)\)。”

这篇论文的目标是找到一个行动策略 \(a(X)\) 和一个证书 \(\nu(X)\)，在满足安全约束的前提下，最大化这个有保证的效用。

为什么预测集是答案

历史上，不确定性量化通常依赖于共形预测 (Conformal Prediction, CP) , 它产生预测集 \(C(X)\)。这些是保证以高概率包含真实标签的子集:

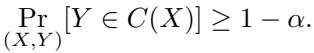
概率不等式显示 Y 在 C(X) 中的概率大于或等于 1 减去 alpha。

这篇论文的一个主要理论贡献是回答了这个问题: 为什么我们要使用预测集？

作者证明，对于风险厌恶型决策者, 预测集是一个充分统计量 (sufficient statistic) 。 这意味着，针对风险厌恶目标进行优化，在数学上等同于设计一个最优的预测集，然后对其应用特定的决策规则。

最大最小决策规则 (Max-Min Decision Rule)

如果你得到一个预测集 \(C(X)\)，并且知道它 (以高概率) 包含真实标签，你应该如何行动？

如果你是风险厌恶型的，你会假设环境是敌对的。你会查看集合 \(C(X)\) 内所有可能的标签，想象最坏的一个 (即对于给定的行动，效用最低的那个) ，然后选择在那种最坏情况下能带来最好结果的行动。

这在形式上被称为最大最小决策规则 :

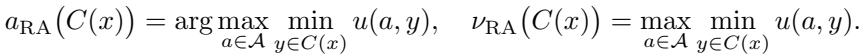
方程定义风险厌恶行动和效用为集合上最小效用的最大化参数。

作者证明了这个简单的规则是极小极大最优 (minimax optimal) 的。如果你只知道真实标签在 \(C(X)\) 内，这种策略可以保护你免受符合该知识的最坏数据分布的影响。

等价定理

论文中最引人注目的理论结果是一般决策问题 (RA-DPO) 与预测集优化问题 (RA-CPO) 之间的等价性。

作者表明，你不需要在所有可能的策略上解决复杂的优化问题。相反，你可以完全专注于设计“最佳”预测集——这里的“最佳”意味着最大化最大最小效用的集合——然后简单地应用最大最小规则。如果你构建了最优预测集，你就自动推导出了最优的风险厌恶策略。

设计最优预测集

我们已经确定我们需要预测集，并且知道一旦有了它们该如何行动。但并非所有的预测集都是生而平等的。我们可以通过每次都返回包含所有标签的集合 (例如，“诊断结果要么是健康，要么是肺炎，要么是 COVID”) 来满足覆盖率保证。这是安全的，但毫无用处——它的效用为零。

我们需要使集合尽可能小且信息量大，以最大化效用。论文将其表述为风险厌恶共形预测优化 (Risk Averse Conformal Prediction Optimization, RA-CPO) :

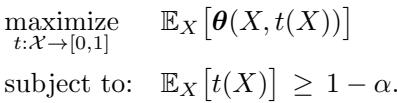
优化问题: 在预期覆盖率大于 1 减去 alpha 的约束下，最大化预期 theta。

为了解决这个问题，作者引入了该问题的一种新颖的重新参数化方法，涉及两个关键函数: \(\boldsymbol{\theta}\) 和 \(\boldsymbol{g}\)。

理解 \(\theta(x, t)\)

函数 \(\theta(x, t)\) 代表如果分配给我们 \(t\) 的“覆盖预算”，针对特定输入 \(x\) 可实现的最大风险厌恶效用。

想象一下，你被迫以概率 \(t\) 覆盖真实标签。你会选择那些最可能的标签集合，使其概率总和达到 \(t\)。然后，你会选择在该集合上最大化最小效用的行动。\(\theta(x, t)\) 就是由此产生的效用值。

最优集合的结构

利用对偶理论，作者展示了最优预测集具有特定的结构，该结构由单个标量参数 \(\beta\) 控制。

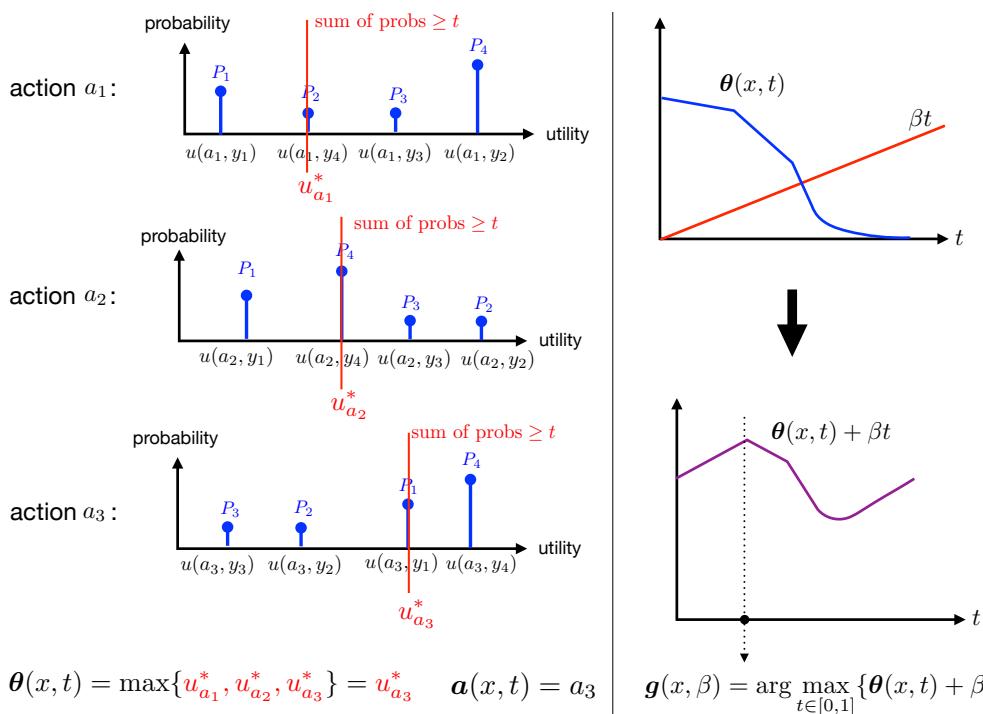
theta 和 g 函数的可视化演示。左图显示离散的行动和概率。右图显示 theta 与 t 的关系曲线。

如图 2 所示:

  1. 左图: 对于给定的覆盖概率 \(t\)，我们计算最佳的最坏情况效用 \(\theta(x, t)\)。
  2. 右图: 我们需要为每个特定输入 \(x\) 选择最优覆盖 \(t^*(x)\)。这是通过最大化 \(\theta(x, t) + \beta t\) 来确定的。

参数 \(\beta\) 充当覆盖的“价格”。它平衡了全局要求 (平均覆盖 95% 的情况) 与最大化效用的局部愿望。最优覆盖分配 \(t^*(x)\) 由函数 \(\boldsymbol{g}(x, \beta)\) 给出:

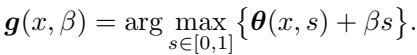
g(x, beta) 定义为 theta 加上 beta 乘以 s 的最大化参数。

这种理论表征非常强大，因为它将复杂的集合设计问题简化为寻找单个最优标量 \(\beta\)。

算法: 风险厌恶校准 (RAC)

理论假设我们知道真实的概率分布。在实践中，我们只有有限的数据集和一个输出估计概率 \(f_x\) 的“黑盒”模型 (如神经网络) 。

作者提出了风险厌恶校准 (RAC) , 这是一个有限样本算法，弥合了理论与实践之间的差距。RAC 的工作原理是将预训练模型作为基础，并校准参数 \(\beta\) 以确保有效的覆盖。

步骤 1: 估计函数

首先，RAC 使用模型的输出 \(f_x\) 来计算效用函数的经验版本，表示为 \(\hat{\theta}(x, t)\) 和 \(\hat{a}(x, t)\):

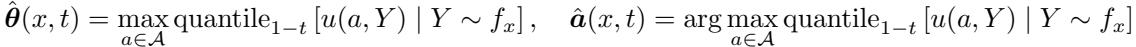
基于模型 f_x 分位数的 hat theta 和 hat a 的定义。

步骤 2: 校准 \(\beta\)

算法的核心是找到正确的 \(\beta\)。我们想要最小的 \(\beta\) (这鼓励更小、更有用的集合) ，同时仍然满足安全约束。

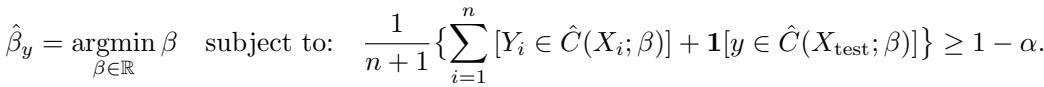
使用校准数据为特定标签 y 寻找 beta hat 的方程。

对于一个测试点 \(x_{\text{test}}\)，算法为每个可能的候选标签 \(y\) 计算一个特定的 \(\beta\)，实际上是在检查: “如果 \(y\) 是真实标签，我需要什么样的 \(\beta\) 才能确保我的集合是有效的？”

步骤 3: 构建集合

最后，预测集 \(C_{\text{RAC}}\) 包含所有在校准后的 \(\beta\) 下“合理”的标签 \(y\):

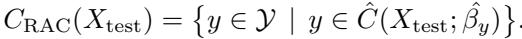
涉及 hat C 和 hat beta 的 RAC 预测集定义。

作者证明了一个关键定理: RAC 满足无分布边际覆盖 (distribution-free marginal coverage) 。

\[ \Pr[Y_{\text{test}} \in C_{\text{RAC}}(X_{\text{test}})] \ge 1 - \alpha \]

这意味着无论真实的底层数据分布如何，RAC 生成的集合都将以期望的概率 (例如 95%) 包含真实标签。因此，由此产生的决策策略满足效用上的安全保证。

实验: 医学与电影

为了展示 RAC 的有效性，作者在两个截然不同的领域进行了测试: 医学诊断 (高风险) 和电影推荐 (低风险但有明确的效用权衡) 。

医学诊断 (胸部 X 光片)

他们使用了 COVID-19 放射显影数据库，将图像分类为四类: 正常、肺炎、COVID-19 和肺部混浊。

他们定义了一个特定的效用矩阵来反映临床现实。例如，未能治疗肺炎 (不采取行动) 的效用为 0 (非常糟糕) ，而给健康人开抗生素的效用为 2 (糟糕，但比死亡好) 。

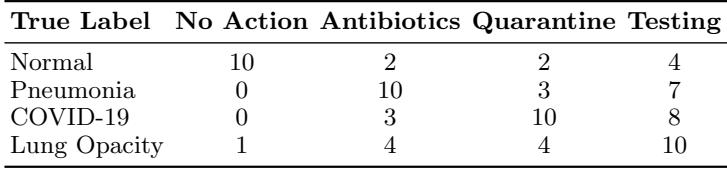
展示医学诊断中行动与真实标签对应效用值的表格。

结果

作者将 RAC 与几个基线进行了比较:

  1. 最佳响应 (Best Response) : 一种信任模型概率并最大化预期效用的标准方法。
  2. 共形预测 + 最大最小 (Conformal Prediction + Max-Min) : 使用标准共形评分 (如“Score-1”或“Score-2”) 构建集合，然后应用最大最小规则。

结果凸显了 RAC 的优势:

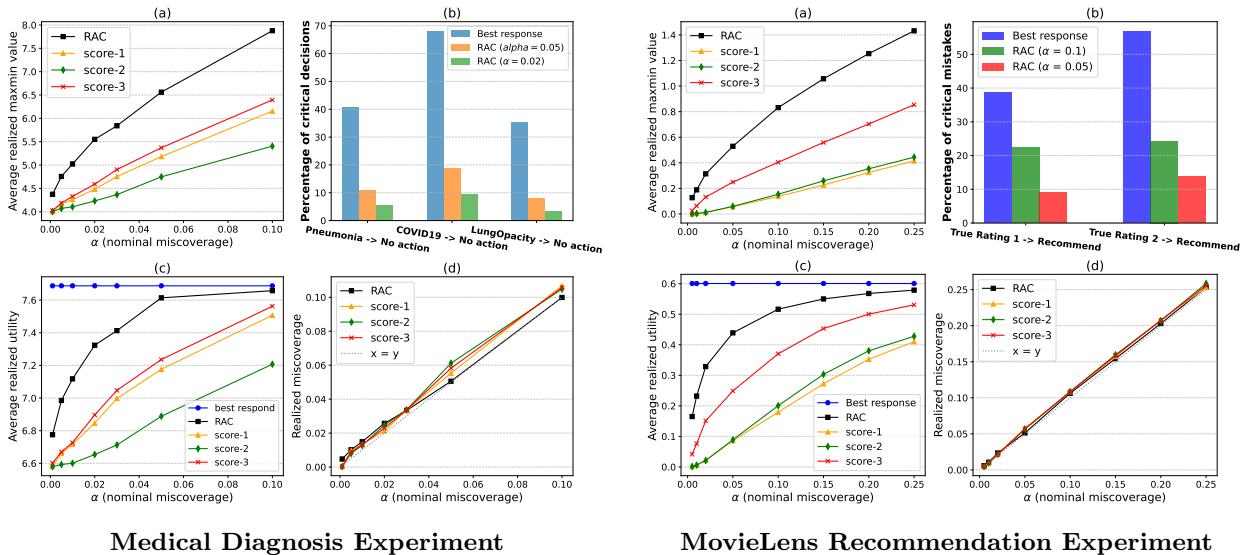
展示平均实现最大最小值、关键错误比例、平均效用和覆盖失效情况的图表。

图 3 的主要结论:

  • 图 (a): 在不同的风险水平 (\(\alpha\)) 下，RAC (黑色方块) 始终比其他共形方法实现更高的“效用证书” (最大最小值) 。这意味着它提供了更强的保证。
  • 图 (b) - 关键错误: 这是对安全性最重要的图表。“最佳响应”方法 (蓝色柱状图) ——忽略了预测集——犯了大量的关键错误。在 COVID-19 案例中，由于追求预期效用，它在超过 60% 的时间里建议“不采取行动”。RAC (橙色/绿色柱状图) 将这一错误率大幅降低 (低于 10%) 。
  • 图 (c): 虽然最佳响应方法在技术上具有较高的平均效用，但 RAC 优于其他安全 (基于预测集) 的方法。它找到了既安全又不过度保守的“最佳平衡点”。

实验证实，在高风险环境中简单地“信任模型” (最佳响应) 是危险的。标准的共形预测虽然安全，但可能效率低下。RAC 专门针对下游决策优化了集合结构，提供了两全其美的方案: 严格的安全性和高效用。

结论与启示

这篇论文建立了共形预测与决策理论之间的基础联系。它证明了预测集不仅仅是不确定性的启发式方法；它们是风险厌恶型决策的最优充分统计量。

通过使用风险厌恶校准 (RAC) ，医疗保健或自动驾驶等安全关键领域的从业者可以:

  1. 采用任何黑盒模型。
  2. 为其包裹一层严格的安全层。
  3. 生成最优行动策略，在最大化效用的同时，保证灾难性风险保持在用户定义的阈值以下。

虽然目前的工作侧重于边际保证 (总体平均) ，但该框架为未来扩展到群组条件或标签条件安全奠定了基础，推动我们更接近于在风险最高时可以信任的 AI 系统。