引言

如果你曾使用过 Transformer (当前 AI 革命背后的核心架构) ，你应该知道它们有一个独特的怪癖: 它们本质上是集合函数 (set functions) 。如果你给 Transformer 输入句子“The cat sat on the mat”或“mat on sat cat The”，其核心注意力机制处理它们的方式几乎完全相同。它没有内在的顺序或空间概念。

为了解决这个问题，我们使用 位置编码 (Position Encodings, PEs) 。 对于大语言模型 (LLMs) ，行业标准已变为 RoPE (旋转位置嵌入，Rotary Position Embeddings) 。 RoPE 对于 1D 文本序列非常有效。然而，当我们把 Transformer 推向机器人技术和计算机视觉领域时，我们要处理的不再仅仅是单词序列，而是 2D 图像、3D 点云以及在物理空间中移动的机器人肢体。

在这些更高维度中，我们该如何表示位置？简单地将 1D RoPE 硬套到 3D 中往往只能得到次优的结果。

在这篇文章中，我们将深入探讨一篇名为 “Learning the RoPEs: Better 2D and 3D Position Encodings with STRING” 的新论文。研究人员提出了 STRING , 这是一个统一的理论框架，不仅推广了 RoPE，还在视觉和机器人任务中显著提升了性能。

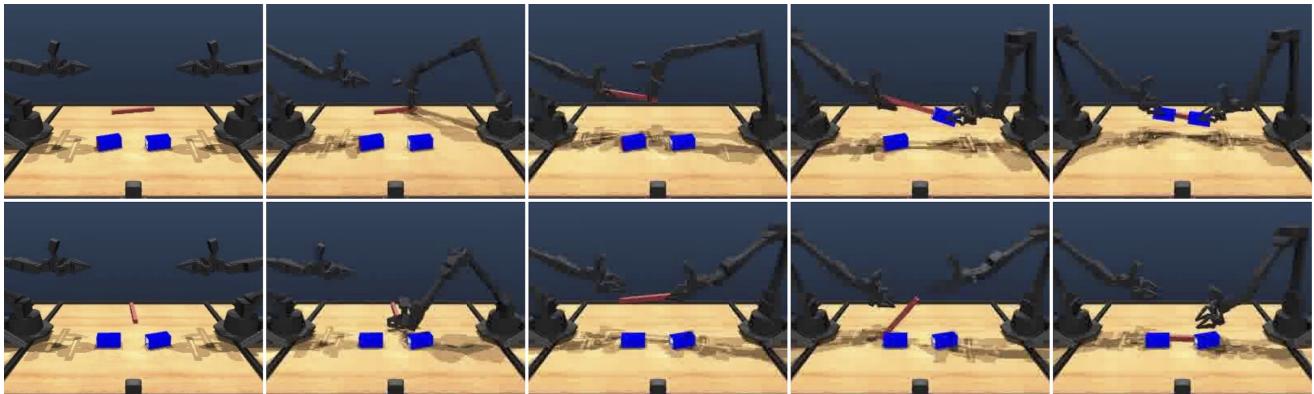
正如上图 1 所示，这种差异不仅仅是学术上的。在复杂的机器人操作任务中，使用 STRING 可能决定了机器人是成功堆叠积木，还是无助地胡乱挥舞。

背景: 为什么位置很重要

在理解 STRING 之前，我们需要了解它所处的背景。

在标准的 Transformer 注意力机制 (如下面的公式 1) 中，查询 (Query, \(\mathbf{q}\)) 和键 (Key, \(\mathbf{k}\)) 之间的相似度是通过点积计算的。

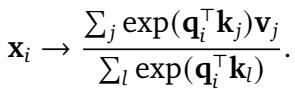
问题在于，无论 \(i\) 和 \(j\) 在序列中的位置如何，\(\mathbf{q}_i^\top \mathbf{k}_j\) 都会产生相同的标量结果。

RoPE 的崛起

为了解决这个问题，研究人员开发了旋转位置嵌入 (RoPE) 。与原始的“Attention Is All You Need”论文中将位置向量加到输入中不同，RoPE 根据位置 旋转 查询和键向量。

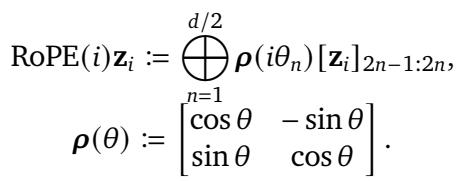
在数学上，RoPE 将向量乘以一个由旋转矩阵组成的块对角矩阵。RoPE 的“魔力”在于 平移不变性 (Translational Invariance) 。 两个 token 之间的注意力分数仅取决于它们之间的相对距离 (\(j - i\)) ，而不是它们的绝对位置。

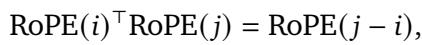
这一属性对于泛化至关重要。如果模型学会了识别句子开头的短语“deep learning”，平移不变性确保它也能识别句子末尾的该短语。

高维空间的问题

当研究人员将 RoPE 应用于 2D 图像或 3D 数据时，他们通常使用一种“分解”方法。他们独立处理 x、y 和 z 坐标，并分别对每个坐标应用 1D RoPE，实际上是将它们堆叠起来。

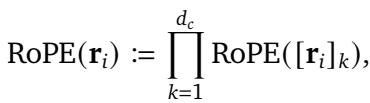
虽然这种方法效果尚可，但它在某种程度上是权宜之计。它假设空间维度之间的相互作用可以通过独立的旋转来简单建模。STRING 的作者认为，存在一种更通用、数学上更严谨的方法来处理位置，这种方法可以自然地扩展到任何维度。

核心方法: 介绍 STRING

STRING 代表 Separable Translationally Invariant Generalized Position Encodings (可分离平移不变广义位置编码) 。

该论文的核心洞察源于 李群理论 (Lie Group theory) 。 研究人员意识到 RoPE 只是更广泛变换类别中的一个特定实例。他们提出的问题是: 变换查询和键的最通用方式是什么，才能使它们的点积保持平移不变性？

通用公式

作者使用矩阵指数定义了 STRING。STRING 不使用固定的旋转矩阵，而是使用一组可学习的 生成元 (generators) (\(\mathbf{L}_k\))。

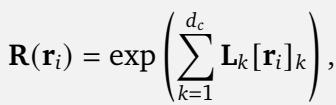
这里，\(\mathbf{r}_i\) 是位置向量 (可以是 1D、2D 或 3D) 。位置编码通过矩阵乘法应用:

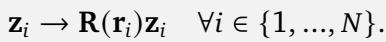
为了使其有效——具体来说，为了使编码 可分离 (分别独立应用于查询和键) 且具有 平移不变性——生成元 \(\mathbf{L}_k\) 必须满足特定属性。它们必须是 斜对称的 (skew-symmetric) (意味着 \(\mathbf{L}^\top = -\mathbf{L}\)) ，并且它们必须 对易 (commute) (乘法顺序不影响结果) 。

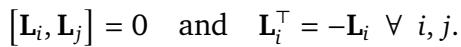
这为什么很酷? 作者证明了一个强有力的定理: STRING 是 (使用矩阵乘法的) 最通用的平移不变位置编码算法 。

这意味着 RoPE 实际上只是 STRING 的一种特定“风味”。如果你手动选择生成元 \(\mathbf{L}\) 使其看起来像特定的块对角矩阵，你就得到了 RoPE。但如果你从数据中 学习 这些生成元，你可以找到更适合特定任务 (如 3D 深度感知) 的位置编码。

提高效率: Cayley 和 Circulant STRING

你可能会想: “矩阵指数？听起来计算成本很高。” 你是对的。为每个 token 计算密集 \(d \times d\) 矩阵的指数对于训练大型模型来说太慢了 (\(O(d^3)\) 复杂度) 。

为了使 STRING 具有实用性，作者引入了两种高效变体，在保持理论优势的同时保持较低的计算开销。

1. “新基底中的 RoPE”技巧

作者证明，任何 STRING 编码都可以重写为夹在两个正交矩阵 \(\mathbf{P}\) 之间的 RoPE。

这意味着我们可以通过简单地采用标准 RoPE 并学习一个变换矩阵 \(\mathbf{P}\) 来实现 STRING，该矩阵在应用位置编码之前将数据旋转到更好的基底中。这非常高效，因为 RoPE 是稀疏的 (大部分为零) ，所以计算速度很快。

2. Cayley-STRING

参数化这个正交矩阵 \(\mathbf{P}\) 的一种方法是使用 凯莱变换 (Cayley Transform) 。 它避免了昂贵的矩阵求逆运算，并确保矩阵在训练期间保持正交。

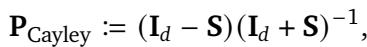
3. Circulant-STRING

另一种高效变体使用 循环矩阵 (Circulant Matrices) 。 循环矩阵由单个向量定义，其中每一行都是上一行的旋转版本。

由于其结构，循环矩阵的运算可以使用快速傅里叶变换 (FFT) 极其快速地计算 (\(O(d \log d)\)) 。这使得 Circulant-STRING 成为速度优先时的绝佳选择。

实验与结果

研究人员不仅停留在数学层面；他们在各种任务中测试了 STRING，范围从标准图像分类到复杂的机器人操作。

1. 通用视觉任务 (2D)

第一个测试场是标准计算机视觉。他们在 ImageNet (分类) 和 WebLI (图像-文本检索) 上测试了 STRING。

在 ImageNet 分类中，STRING 变体 (Cayley 和 Circulant) 优于标准 ViT 和 RoPE。虽然 ImageNet 上的提升幅度通常较小，但在某些配置中，STRING 提供了相对于常规 ViT 大于 1% 的绝对增益，且额外参数几乎可以忽略不计。

2. 3D 物体检测

当我们转向 3D 时，事情变得更有趣了。作者修改了 OWL-ViT 架构以预测 3D 边界框，而不仅仅是 2D 边界框。

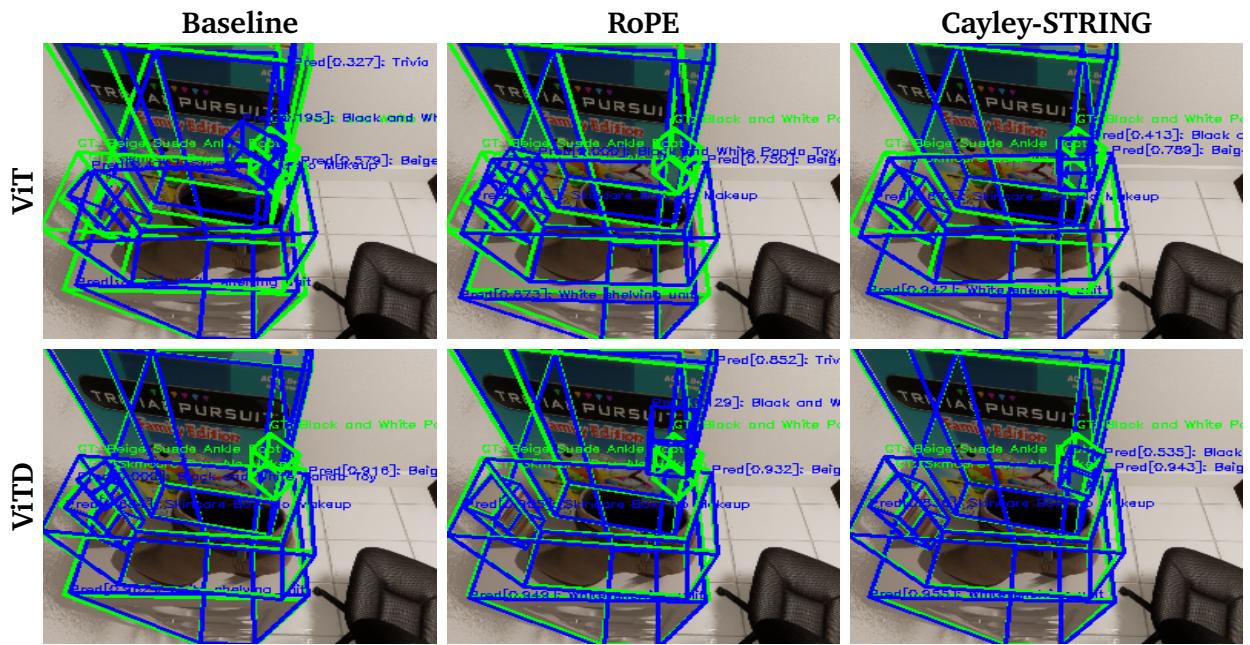
如上图 2 所示，Cayley-STRING 模型 (右栏) 生成的 3D 边界框 (蓝色) 比基线和 RoPE 更加紧致和准确。置信度分数通常也更能指示物体的存在。

在定量上，STRING 模型提供了显著的改进。对于带有深度输入的 Vision Transformer (ViTD)，Cayley-STRING 相比最佳 RoPE 变体提供了 2% 的相对提升 。 这表明学习到的基底使模型能够更好地解释 2D 像素与 3D 深度之间的关系。

3. 机器人技术: 终极测试

最令人信服的结果来自使用 ALOHA 仿真和真实世界 KUKA 机器人的机器人操作任务。机器人技术需要精确的空间推理——准确知道抓手相对于杯子的位置至关重要。

ALOHA 仿真

团队在 12 项灵巧操作任务上测试了模型，例如“HandOverBanana” (递香蕉) 、“DoubleInsertion” (双重插入) 和“MugOnPlate” (放杯子在盘子上) 。

他们比较了基线 Vision Transformer (ViT)、RoPE 和 STRING。结果非常明确:

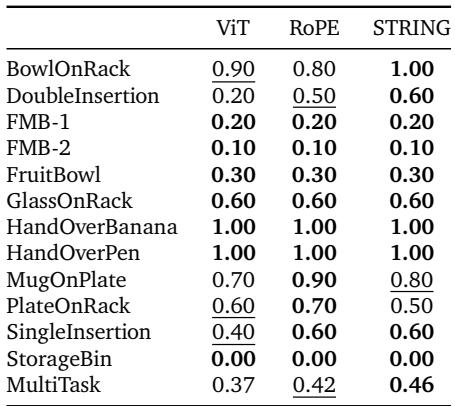
STRING (特别是 Cayley-STRING) 在 13 项任务中的 11 项 取得了最佳成功率。在“MultiTask”综合得分中，它以稳固的优势击败了 RoPE (0.46 vs 0.42) 。

此外，STRING 学得 更快。下图 4 显示了训练曲线。你可以看到浅蓝线 (STRING) 始终高于其他线，在训练过程中更早收敛到更高的成功率。

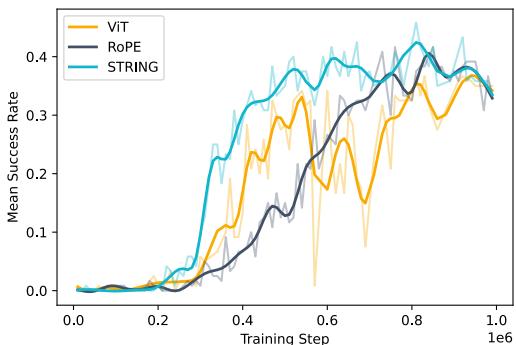
真实世界的鲁棒性

最后，团队将这些策略部署在真实的 KUKA 机械臂上。他们尝试了将 3D 深度数据输入模型的不同方法。

机器人技术中的常用技术是将深度转换为“表面法线图 (Surface Normal Maps, nmap) ”并将其作为图像输入。然而，深度传感器是有噪声的。研究人员发现，添加有噪声的法线图实际上 损害 了标准 2D 基线的性能 (成功率从 65% 降至 42%) 。

STRING 登场。 当他们使用 STRING 直接编码 3D 位置 (将图块提升至 3D) 时，性能跃升至 74% 。

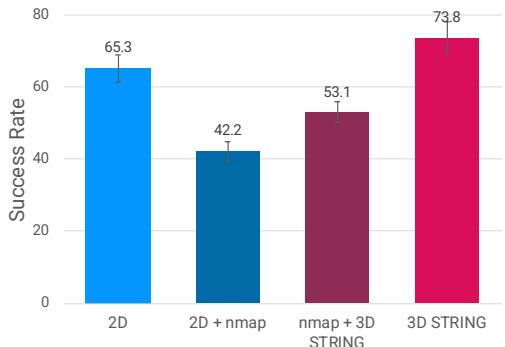
图 5 显示了这一巨大的差异。STRING 稳健处理 3D 坐标的能力使策略能够忽略那些会混淆标准卷积或基于 nmap 方法的传感器噪声。

他们还在 分布外 (Out-Of-Distribution, OOD) 场景中测试了机器人——改变光照、桌子高度或添加干扰物。

如图 6 所示，3D STRING 策略 (品红线) 比 2D 基线 (蓝线) 更具鲁棒性。在“大型干扰物 (Large Distractors) ”的情况下 (中间) ，2D 模型的性能崩溃，而 STRING 保持了高准确率。“桌子高度 (Table Height) ”的变化尤为说明问题——标准相机很难看出桌子低了 10 厘米，但具有深度感知的 STRING 编码策略可以轻松处理。

图 7 可视化了机器人在成功执行任务期间“看到”的内容 (RGB 和深度热力图) 。尽管环境杂乱，模型仍能有效地关注相关物体。

结论与启示

论文 “Learning the RoPEs” 提供了位置编码的一个引人注目的进化方向。通过退一步并透过李群理论的视角审视位置编码，作者推导出了 STRING : 一种理论上合理、计算高效且在实证上更优越的方法。

主要收获:

1. RoPE 是 STRING 的子集: 通过 学习 变换基底，我们可以做得比固定旋转更好。
2. 3D 很重要: 虽然 RoPE 对文本很有效，但 STRING 在机器人和 3D 感知等具有复杂空间几何结构的领域大放异彩。
3. 效率已解决: 通过 Cayley 变换和循环矩阵，我们可以在不拖慢模型速度的情况下获得这些好处。

对于具身智能和计算机视觉的学生及从业者来说，这代表着从临时的空间处理技巧向统一、可学习的几何方法转变。随着我们要求机器人在非结构化 3D 环境中执行越来越复杂的任务，像 STRING 这样的工具很可能会成为神经网络架构技术栈中的标准组件。