在当今的人工智能领域，我们很少从零开始训练模型。相反，我们站在巨人的肩膀上: 我们采用一个庞大的预训练模型 (如 Llama、Gemma 或 ResNet) ，并在特定数据集上对其进行“微调”，以执行特定任务，例如医疗诊断或数学推理。

然而，机器中存在一个幽灵。当模型学习新任务时，它们有一个糟糕的习惯，就是会抹去它们已经知道的内容。这种现象被称为灾难性遗忘 (Catastrophic Forgetting) 。 你教一个模型解决数学问题，突然它就忘记了如何构造语法正确的句子，或者失去了它的通用推理能力。

历史上，标准的解决方案是在新训练阶段“重放”旧数据。但是，如果你没有旧数据怎么办？在许多现实场景中，我们要么下载一个模型权重文件 (例如 Llama 3) ，但无法访问用于训练它的 PB 级专有互联网数据。我们处于一个数据不可知 (data-oblivious) 的设定中。

在最近的一篇论文中，研究人员提出了一种反直觉但强大的解决方案，称为 FLOW (Fine-tuning with Pre-trained Loss-Oriented Weighting，基于预训练损失导向权重的微调) 。他们的洞察颠覆了标准的机器学习智慧: 为了更好地记忆，我们不应该关注那些“困难”的例子来学得更快，而应该关注那些“简单”的例子。

问题所在: 微调的悖论

微调是一种微妙的平衡行为。理想情况下，我们希望同时实现两个目标:

  1. 可塑性 (Plasticity) : 模型必须更改其参数以学习新的下游任务。
  2. 稳定性 (Stability) : 模型必须保留预训练期间学到的表示，以维持通用能力。

当我们使用标准方法 (如最小化交叉熵损失) 进行微调时，优化算法会无情地更新参数以适应新数据。如果新任务的梯度指向与原始知识正交的方向，模型就会偏离其预训练状态。

“数据不可知”设定的约束

大多数现有的对抗灾难性遗忘的技术都假设你对预训练数据有所了解。

  • 重放方法 (Replay Methods) : 存储旧图像/文本的缓冲区并将其混合进去。 (如果你没有数据，这就不可能) 。
  • 正则化 (例如 EWC) : 惩罚对重要参数的更改。 (计算成本高昂，且通常需要旧数据的费雪信息矩阵) 。

FLOW 的作者解决了这个问题最困难的版本: 你只有预训练模型 (\(\theta^*\)) 和新数据集。除此之外别无他物。

核心方法: FLOW

研究人员提出的解决方案 FLOW 完全在样本空间中运行。它不需要修改模型架构或存储梯度。它只是问: 新数据集中的哪些样本是“安全”的学习对象？

直觉: 简单样本 vs. 困难样本

在标准的机器学习中，我们通常优先考虑“困难”样本——那些损失高的样本——因为它们包含最多的学习信号。如果模型预测错误，我们要纠正它。

FLOW 采取了相反的方法来减轻遗忘。

  • 简单样本 (Easy Samples) : 这些是微调集中的数据点，预训练模型在这些点上已经实现了低损失。它们与模型的现有知识一致。
  • 困难样本 (Hard Samples) : 这些是预训练模型具有高损失的数据点。积极地学习这些样本需要对模型参数进行显著更改，从而导致漂移。

假设很简单: 通过提高简单样本 (预训练损失低的地方) 的权重，我们引入了一种“监督偏差”，使梯度与预训练模型保持一致。

算法

FLOW 算法简洁优雅。它包含三个步骤:

  1. 推理: 将新的微调数据集通过冻结的预训练模型。
  2. 加权: 根据步骤 1 中产生的损失为每个样本分配一个权重 \(w_i\)。较低的损失获得较高的权重。
  3. 训练: 使用这些计算出的权重在新数据集上微调模型。

数学基础

为了推导最佳加权方案，作者将问题框架化为一个优化任务。我们希望找到一个权重分布 \(\pi\)，它偏向于具有低预训练损失 (\(f_i(\theta^*)\)) 的样本，同时保持一定程度的均匀性 (我们不想只在一个样本上训练) 。

这是通过最小化以下目标函数来实现的:

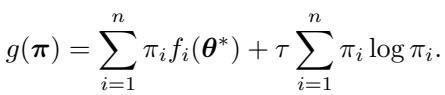
目标函数最小化方程。

在这里，第一项最小化预训练模型上的加权损失，第二项是负熵正则化 , 由温度参数 \(\tau\) 控制。这个熵项确保权重不会坍缩到一个点上。

使用拉格朗日乘数法求解此优化问题，可以得出第 \(i\) 个样本的最佳权重:

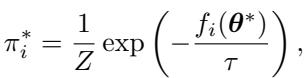
显示最佳权重计算的方程。

这个结果非常迷人，因为它看起来像一个 softmax 函数，但在指数内部有一个负号。这证实了权重 \(\pi^*_i\) 与预训练损失成反比。

与分布鲁棒优化 (DRO) 的对比

将 FLOW 与分布鲁棒优化 (DRO) 进行对比很有帮助。DRO 旨在通过关注最坏情况场景使模型具有鲁棒性。它的目标函数如下所示:

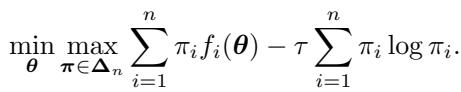
分布鲁棒优化方程，显示最大化。

注意对 \(\pi\) 的 max 操作。DRO 试图找到使损失最大化的权重，迫使模型在困难样本上改进。DRO 的解分配的权重与 \(\exp(f_i(\theta)/\tau)\) 成正比。

FLOW 做的恰恰相反。它通过坚持简单样本来最小化漂移。它实际上是在说: “让我们学习新任务，但让我们优先考虑那些不需要我们从根本上重写神经网络路径的数据点。”

实现 FLOW

在实践中，算法实现如下。对于数据集对 \((\mathbf{x}_i, \mathbf{y}_i)\):

  1. 计算权重: \(w_i = \exp\left(-\frac{f_i(\boldsymbol{\theta}^*)}{\tau}\right)\)。
  2. 计算加权损失:

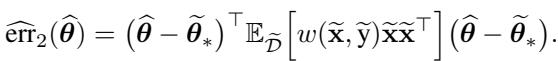
用于训练的最终加权损失函数方程。

  1. 最小化此损失以找到微调后的参数 \(\widehat{\theta}^*\)。

作者提供的一个关键启发式方法是温度 \(\tau\) 的选择。他们将 \(\tau\) 设置为预训练损失的中位数 。 这使得该方法本质上是无参数的，消除了昂贵的超参数调整需求。

理论分析: 为什么它有效

作者使用线性模型提供了严格的分析，以解释 FLOW 的几何效应。

在线性设置中，我们可以根据参数与最优解的距离来定义预训练任务 (\(\mathrm{err}_1\)) 和微调任务 (\(\mathrm{err}_2\)) 的总误差。

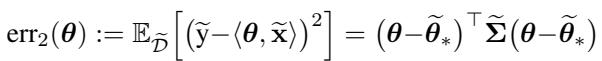
预训练任务的误差 1 定义。 微调任务的误差 2 定义。

当我们执行标准微调 (Vanilla FT) 时，模型会从预训练权重 (\(\theta^*\)) 迅速移向微调最优点 (\(\tilde{\theta}^*\)) 。分析表明，这种移动非常激进，不易阻挡。

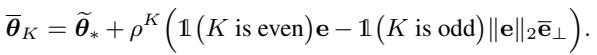
显示标准微调轨迹的方程。

然而，使用 FLOW 时，轨迹发生了变化。加权方案有效地改变了优化器“看到”的数据的协方差矩阵。加权协方差矩阵 \(\tilde{\Sigma}'\) 推导如下:

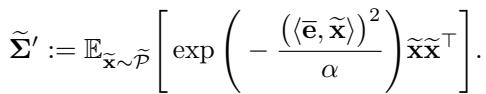
加权协方差矩阵方程。

通过一系列涉及该新矩阵特征向量的推导，作者表明 FLOW 阻滞了特定方向的学习。

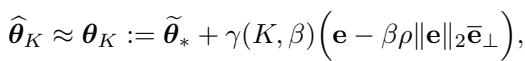
显示 FLOW 微调轨迹的方程。

具体来说，FLOW 阻滞了沿着误差向量 \(\mathbf{e}\) 方向的收敛。这种“阻滞”防止了模型过度拟合微调任务并破坏预训练的表示。它本质上起到了软刹车的作用，允许模型在不失去其特性的情况下进行适应。

实验与结果

作者在计算机视觉 (ResNet) 和大型语言模型 (Gemma, Llama) 上测试了 FLOW。结果一致表明，FLOW 在学习新任务和记住旧任务之间取得了卓越的平衡。

视觉任务 (ResNet-50)

团队在几个下游数据集 (如 CIFAR-10、Cars 和 Flowers) 上微调了 ResNet-50 模型 (在 ImageNet-1K 上预训练) 。他们测量了两件事:

  1. 目标准确率 (Target Accuracy) : 它在新数据集上表现如何？
  2. 预训练准确率 (Pre-training Accuracy) : 它在 ImageNet 上表现是否依然良好？

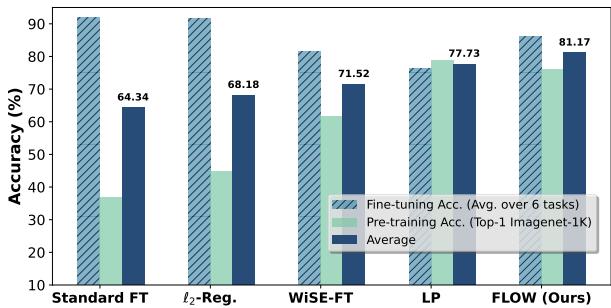
条形图比较 FLOW 与 Standard FT 和 L2 正则化等基线。

如上图 Figure 1 所示，标准微调 (FT) 实现了很高的目标准确率 (~87%) ，但破坏了预训练性能，从近 80% 降至 ~34%。

FLOW (红色条) 保持了 ~77% 的预训练准确率 (几乎没有变化！) ，同时在目标任务上仍达到了 ~85%。当你查看平均 (Average) 指标 (灰色条) 时，FLOW 是明显的赢家，优于 L2 正则化和 WiSE-FT。

为了可视化这种权衡，我们可以看下面的散点图。理想的方法应位于右上角 (高微调准确率，高 ImageNet 准确率) 。

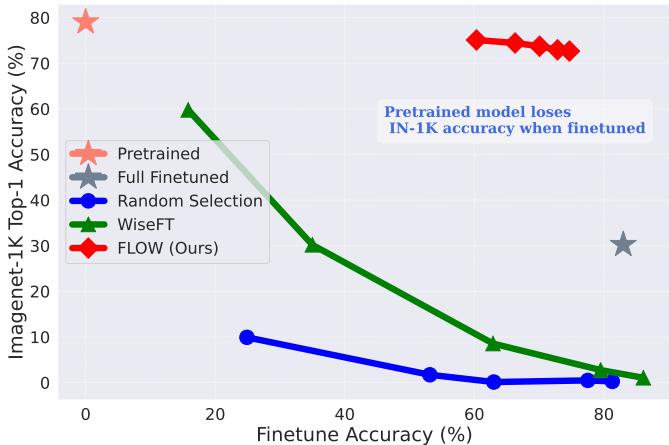
散点图显示微调准确率与预训练准确率之间的权衡。

标准微调 (向右下方移动的曲线) 获得了微调准确率，但在 ImageNet 准确率上崩溃了。FLOW (红色菱形) 在 Y 轴上保持得高得多，保持了鲁棒性。

语言模型 (LLMs)

LLM 的风险更高。作者在数学数据集 (MetaMathQA) 上微调了 Gemma 2B 和 Llama 3.2 3B，并测试了模型是否“忘记”了通用知识 (通过 MMLU 和 Commonsense QA 等基准测试) 。

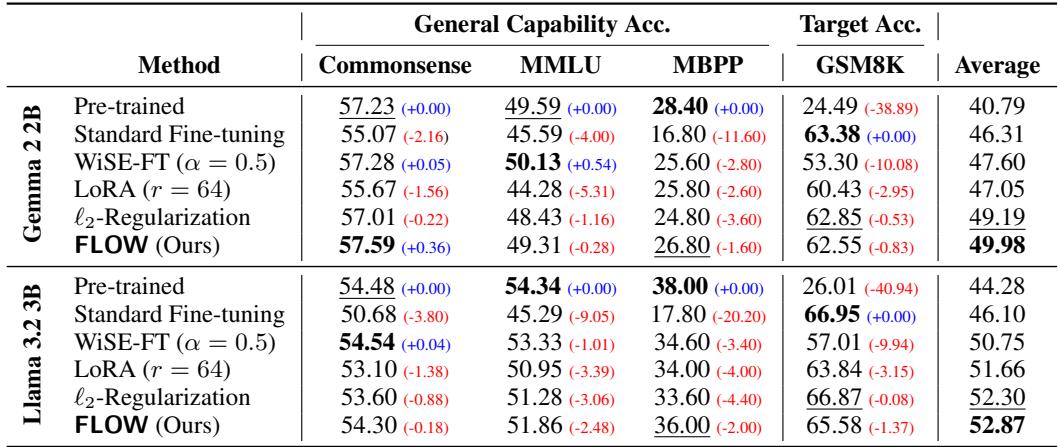
表格显示 FLOW 在 LLM 上与基线的性能对比。

Table 2 强调了结果:

  • 标准微调显著提高了数学 (GSM8K) 分数，但导致常识 (Commonsense) 和 MMLU 分数下降。
  • FLOW 实现的数学分数非常接近标准微调 (例如，在 Gemma 上为 62.55 vs 63.38) ，但保留了显著更多的通用能力 。
  • 在 Llama 3.2 上，FLOW 实际上在所有指标上实现了最高的平均分。

它与其他方法兼容吗？

FLOW 最有力的论据之一是它与其他方法正交 。 你可以将其与参数高效方法 (如 LoRA , 低秩适应) 或模型平均方法 (如 WiSE-FT )结合使用。

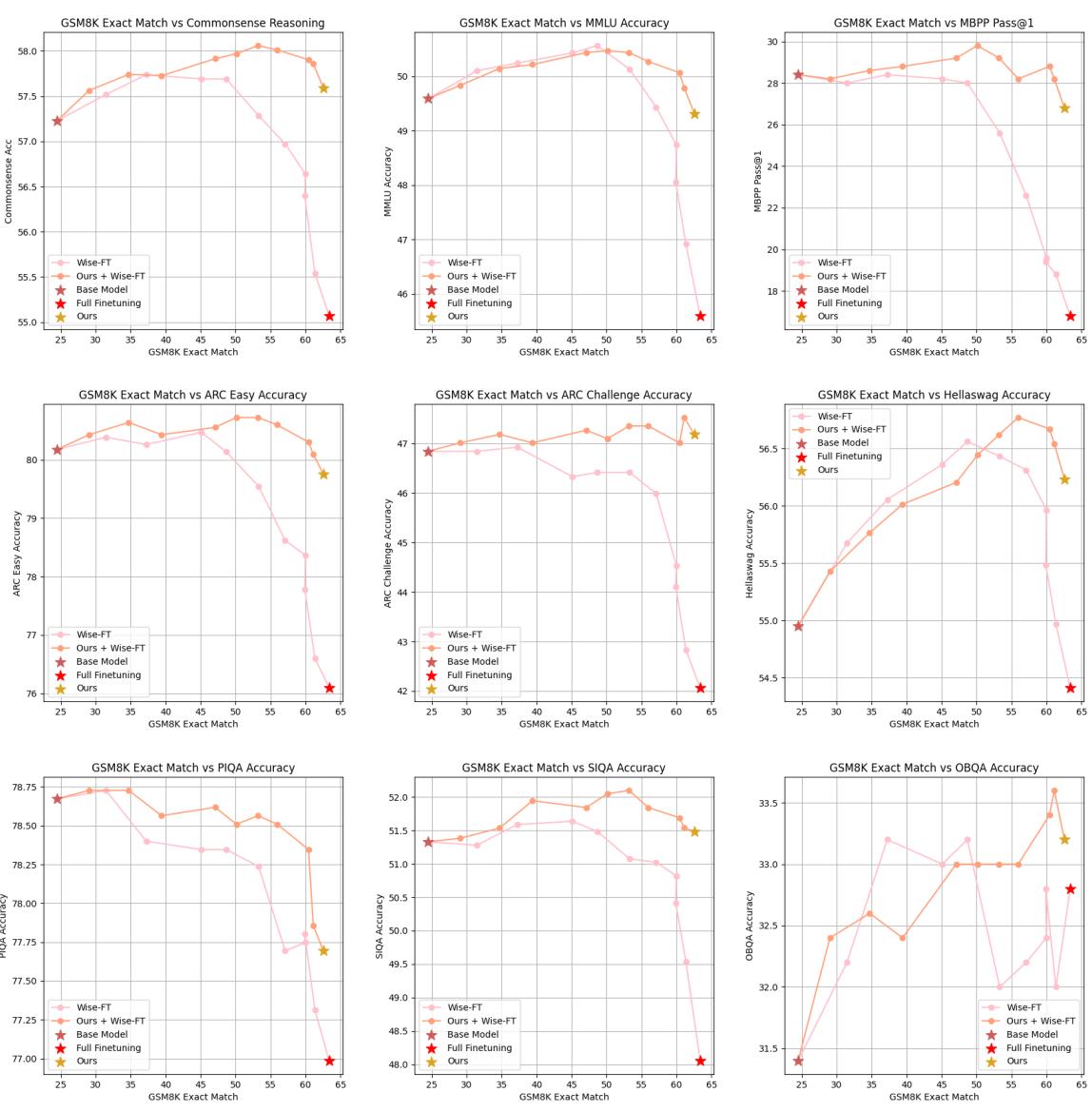
图表网格显示 FLOW 与 WiSE-FT 结合的效果。

Figure 4 展示了将 FLOW 与 WiSE-FT 结合 (橙色线) 通常比单独使用 WiSE-FT (粉色线) 产生更好的结果，将性能前沿进一步推向理想的右上角。

消融实验: 序列加权 vs. Token 加权

对于 LLM，“样本”可以定义为整个序列 (句子/段落) 或单个 Token。作者研究了哪种粒度效果最好。

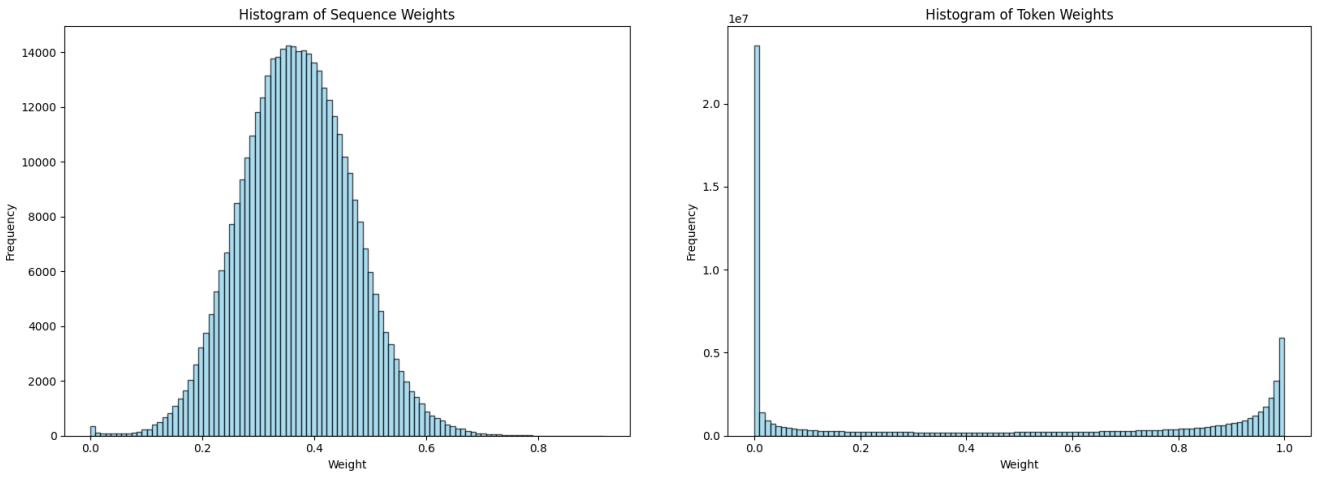
直方图比较序列权重与 Token 权重。

Figure 3 中的直方图揭示了一个关键见解。

  • 左侧 (序列权重) : 权重遵循良好的类高斯分布。权重具有多样性，允许模型有效地进行优先级排序。
  • 右侧 (Token 权重) : 分布极度偏斜。大多数 Token 的权重接近 0 或 1。这种二元行为过度正则化了模型，阻止了它有效地学习新任务。

因此, 序列级加权 (sequence-wise weighting) 是 LLM 的推荐方法。

FLOW 的代价

有什么代价吗？有的。通过上调简单样本的权重，我们隐式地下调了困难样本的权重。在新任务的背景下，“困难”样本通常是那些包含最新颖信息或边缘情况的样本。

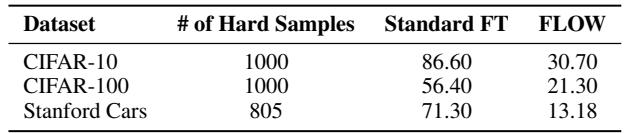
表格显示 FLOW 在困难样本上的表现。

如 Table 5 所示，与标准微调相比，FLOW 在新数据集的“困难样本”特定子集上表现不佳。这是经过计算的牺牲: 我们接受在新任务中最困难的离群点上表现稍差，以确保我们不会发生灾难性遗忘，丢失预训练模型的通用能力。

结论

这篇“上调简单样本权重”的论文为灾难性遗忘问题提供了一个令人耳目一新的视角。在一个痴迷于困难负样本 (hard negatives) 和疑难杂症的领域，FLOW 证明了稳定性来自于简单的路径。

通过简单地计算预训练损失并重新加权新数据，我们可以微调模型以学习新技巧而不忘记旧技巧。这对于“数据不可知”的 AI 来说是至关重要的一步，使我们能够安全地定制强大的开源模型，而无需访问科技巨头的专有数据宝库。

关键要点:

  • 概念: 上调预训练模型已经“理解” (低损失) 的样本权重。
  • 方法: 一个简单、无参数的加权方案 (\(\tau\) = 中位数损失) 。
  • 结果: 在无需访问旧数据的情况下，在视觉和语言模型中实现了最先进的遗忘缓解效果。
  • 实现: 易于添加到现有的训练循环中，并与 LoRA 和其他技术兼容。