在大数据时代，我们面临着一个悖论。一方面，我们需要聚合来自数百万用户设备——智能手机、可穿戴设备和物联网传感器——的信息，以了解群体趋势。另一方面，这些数据通常极具私密性。无论是薪资信息、健康指标，还是屏幕使用时间，用户 (以及法律) 都要求隐私保护。

如何在不收集原始数据的情况下，计算出简单的统计数据，例如薪资中位数或应用使用时长的第95百分位？

这就是分布式隐私分位数估计 (Distributed Private Quantile Estimation) 所面临的挑战。一篇新的研究论文《Lightweight Protocols for Distributed Private Quantile Estimation》 (分布式隐私分位数估计的轻量级协议) 提出了一种利用自适应算法的突破性方法。研究人员证明，通过顺序提问——即下一个问题取决于前一个答案——我们可以用比以前认为的少得多的用户来估计分位数。

在这篇文章中，我们将拆解这篇论文，探索如何结合本地差分隐私 (Local Differential Privacy, LDP) 、噪声二分查找 (Noisy Binary Search) 和洗牌技术 (Shuffling) 来高效地解决这个问题。

问题: 在看不见数值的情况下寻找中位数

假设我们有 \(n\) 个用户。每个用户持有一个秘密数字 \(x_j\)，该数字属于范围 \(\{1, \dots, B\}\)。例如，如果我们查看薪资，\(B\) 可能是 1,000,000。

我们的目标是找到这些值的中位数 (或任何其他分位数) 。在非隐私世界中，我们只需收集所有数字，对其排序，然后选取中间的一个。但在我们的场景中，我们无法看到原始数值。我们必须在本地差分隐私 (LDP) 下进行操作。

什么是本地差分隐私？

在 LDP 模型中，用户不信任服务器。用户不会发送原始数据 \(x\)，而是在其设备上运行一个随机机制 \(\mathcal{M}\) 并发送带有噪声的结果 \(y\)。

Pr[M_i(x)=y] <= e^epsilon * Pr[M_i(x’)=y].

上面的公式定义了 \(\varepsilon\)-LDP。直观地说，它保证了输出 \(y\) 不会过多地泄露关于输入 \(x\) 的信息。如果 \(\varepsilon\) (epsilon) 很小，隐私性就很高，但数据噪声很大。如果 \(\varepsilon\) 很大，数据准确，但隐私性较低。

实现这一点的标准工具是随机响应 (Randomized Response) 。 可以把它想象成在回答“是/否”问题之前抛硬币。如果是正面，你说真话；如果是反面，你随机回答。服务器虽然收到的是噪声答案，但如果有足够多的用户，它仍然可以估计出真实的统计数据。

目标: 经验累积分布函数 (CDF)

为了找到分位数，我们通常关注经验 CDF，记为 \(F_X(i)\)。这个函数告诉我们数值小于或等于 \(i\) 的用户比例是多少。

F_X(i) = 1/n * |{j in [n] | x_j <= i}|.

如果我们想找中位数，我们就是要找一个值 \(m\)，使得 \(F_X(m) \approx 0.5\)。

创新点: 自适应 vs. 非自适应

目前针对该问题的解决方案大多是非自适应的。这意味着服务器在收集任何数据之前就决定了它要问的所有问题。例如，它可能会问用户 1 关于范围 [0-100] 的问题，问用户 2 关于 [0-100] 的问题，问用户 3 关于 [100-200] 的问题。

研究人员指出了这里的一个主要局限: 非自适应协议效率低下。它们需要大量的用户 (与 \(\text{poly}(\log B)\) 成比例) 才能获得准确的结果，因为它们必须“盲目地”覆盖整个定义域。

研究人员提出了一种顺序自适应的方法。

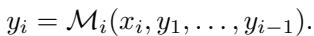
y_i = M_i(x_i, y_1, …, y_{i-1}).

如上式所示，在自适应协议中，发送给用户 \(i\) 的查询取决于从用户 \(1, \dots, i-1\) 收到的答案。这使得算法能够像“猜高低”游戏或二分查找一样，“聚焦”于中位数。

核心方法: 噪声二分查找

这篇论文的核心是将隐私中位数估计问题映射为噪声二分查找 (Noisy Binary Search) 。

在标准的二分查找 (就像在字典中查单词) 中，你会查看中间页。如果你的单词按字母顺序在后面，你就丢弃前半部分，查看后半部分的中间页。你会重复这个过程 \(\log B\) 次。

在隐私设置下，我们无法完美地检查“中间页”。我们可以问一个用户: “你的值是 \(\le m\) 吗？”用户会应用 LDP (添加噪声) 并回答“是”或“否”。由于噪声的存在，我们可能会得到错误的方向。

这将问题转化为在一组排序的硬币中寻找“好硬币”，这些硬币的正面朝上概率是未知的。我们正在寻找一个阈值 \(m\)，在这个阈值处，“是”的回答概率穿过 0.5。

挑战: 不放回采样

这里有一个微妙但关键的技术障碍。在标准的噪声二分查找理论中，我们假设我们可以多次抛同一枚硬币以获得更好的估计。在 LDP 用户设置中, 我们只能查询每个用户一次 。

我们从 \(1\) 到 \(n\) 遍历用户。随着我们消耗用户，剩余的用户池变小了。这意味着在每一步之后，剩余用户的真实中位数会发生轻微偏移。统计分布是非平稳的。

作者通过证明只要我们以随机顺序处理用户，分布就不会发生太大变化来解决这个问题。他们使用鞅 (Martingale) 来对变化的概率进行建模。

Pr[max |X_i| >= t] <= 2 exp(-t^2 n / 2).

通过应用 Azuma 不等式 (如上所示) ，他们证明了经验概率 (“抛硬币”) 的偏差是有界的。具体来说，他们证明了计数发生显著偏差的概率呈指数级下降。

Pr[max |p_j^t - p_j^0| >= alpha] <= 2 exp(-C log B / 2).

这个界限允许他们将偏移的分布视为对抗性噪声二分查找 (Adversarial Noisy Binary Search) 。 即使“硬币概率” (数值 \(\le m\) 的人数比例) 随着我们移除用户而波动，它们也会保持在一个有界范围 (\(\alpha\)) 内。

算法: BayeSS

研究人员利用了一种称为 BayeSS (贝叶斯筛选搜索) 的算法。BayeSS 不仅仅是简单的二分查找，它还维护一个关于中位数可能位置的概率分布 (一种信念) 。

  1. 它选择一个能有效分割这种信念质量的查询点。
  2. 它查询一个用户: “你的值 \(\le\) 查询点吗？”
  3. 它根据带噪声的回答更新信念。

通过将鞅分析与 BayeSS 相结合，作者得出了他们的第一个主要结果。他们可以仅使用以下数量的用户找到一个 \(\alpha\)-近似中位数:

\[O\left(\frac{\log B}{\varepsilon^2 \alpha^2}\right) \text{ 个用户。}\]

这比非自适应方法有了显著改进，后者需要乘以 \(\log B\) 的因子。

结果是一个中位数 \(\tilde{m}_q\)，它以高概率满足精度条件:

Pr[[F_X(m_q), F_X(m_q+1)] intersect (q - alpha, q + alpha) != empty] >= 1 - beta.

洗牌模型: 中间地带

纯 LDP 限制性很强 (噪声很大) 。一个流行的替代方案是洗牌模型 (Shuffle Model) 。 在这里，用户将他们带有噪声的消息发送给一个“洗牌器” (一个受信任的中介) ，洗牌器去除标识符并随机打乱消息顺序，然后再发送给分析器。

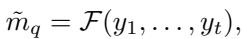
m_q = F(y_1, …, y_t).

洗牌通过“藏身于人群之中”来放大隐私。然而，洗牌需要一批消息才能起作用。你无法对单条消息进行洗牌。这与上述完全自适应的方法 (一次查询一个用户) 相冲突。

作者提出了一种混合方案: 多轮洗牌差分隐私 (Multi-Round Shuffle DP) 。 他们不是一次查询 1 个用户，而是查询一批用户。他们对这批数据进行洗牌，分析结果，然后决定下一批的查询。

他们利用洗牌放大 (Amplification by Shuffling) 的结果表明，隐私保证得到了显著提升。

Pr[(M_t(x_pi(i))) in S] <= e^epsilon * Pr[…] + delta.

这个公式表明，即使本地机制 \(\varepsilon_L\) 较弱 (较大) ，洗牌后的输出也能满足 \((\varepsilon, \delta)\)-DP。

洗牌模型的最终样本复杂度为:

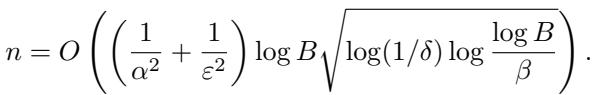
n = O((1/alpha^2 + 1/epsilon^2) log B sqrt(log(1/delta) log(log B / beta))).

该协议本质上运行的是“朴素”二分查找 (将定义域对半分割) ，但利用洗牌的隐私放大作用，使得每个用户所需的噪声大大减少，从而减少了所需的总用户数。

实验: 效果如何？

作者使用合成数据 (帕累托分布和均匀分布) 通过实验验证了他们的理论界限。他们将自己的自适应方法( DpBayeSS )与朴素噪声二分查找 (DpNaiveNBS) 以及一种最先进的非自适应方法分层机制 (Hierarchical Mechanism) 进行了比较。

成功率 vs. 隐私

在下图中，我们可以看到随着隐私预算 \(\varepsilon\) 增加 (x 轴) ，成功率 (y 轴) 的变化。请记住，\(\varepsilon\) 越高意味着噪声越小。

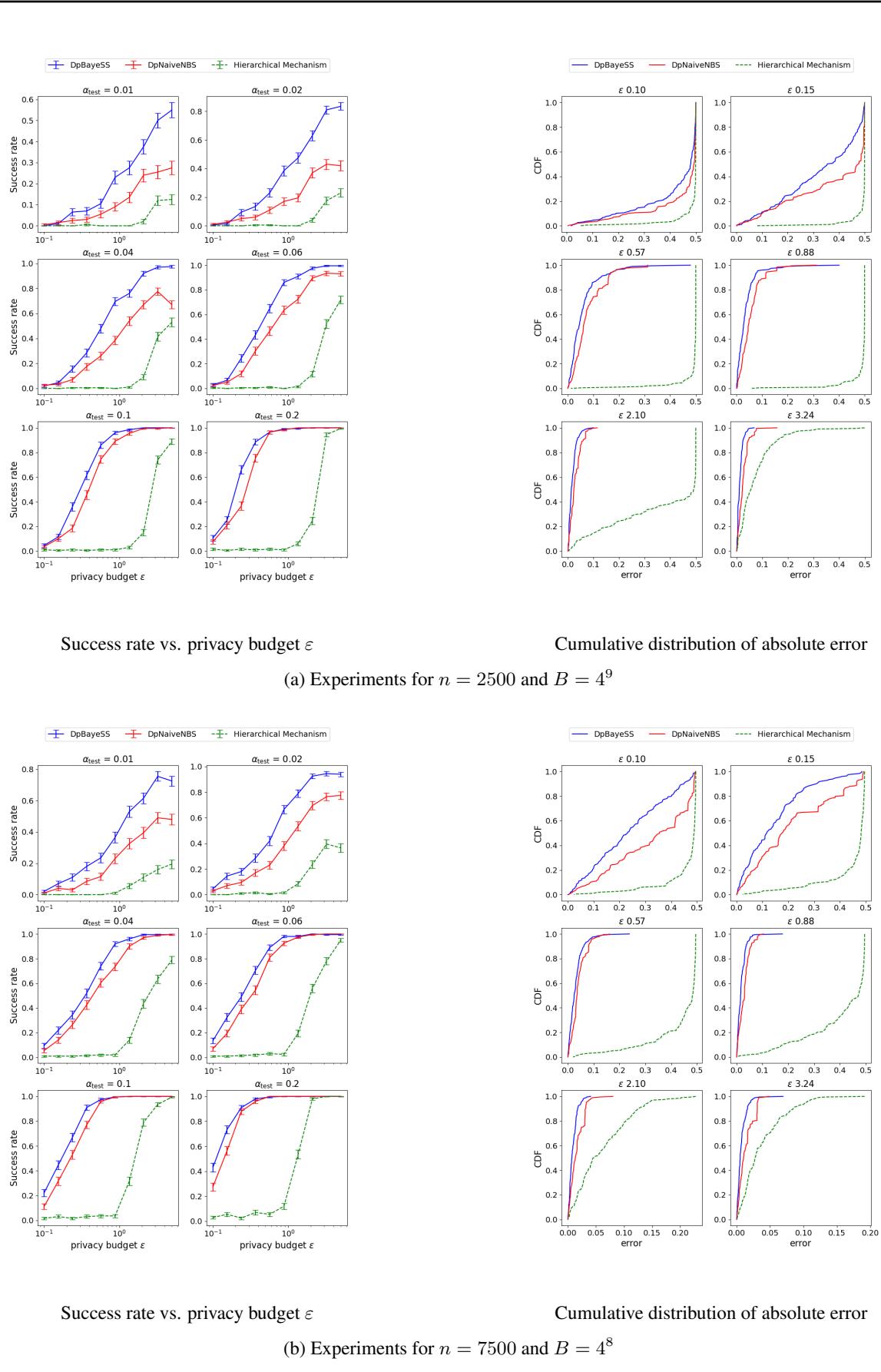
图 5 比较成功率。DpBayeSS (蓝色 +) 的表现始终优于 Naive (红色 x) 和 Hierarchical (绿色三角形) 。

蓝线 (DpBayeSS) 始终比红线 (Naive) 和绿线 (Hierarchical) 获得更高的成功率，特别是在高隐私 (低 \(\varepsilon\)) 区域。考虑到用户数量，分层机制通常无法返回有意义的中位数，这说明了非自适应性的“代价”。

跨域大小的稳定性

主要的理论主张之一是自适应方法随定义域大小 \(B\) 呈对数级扩展。

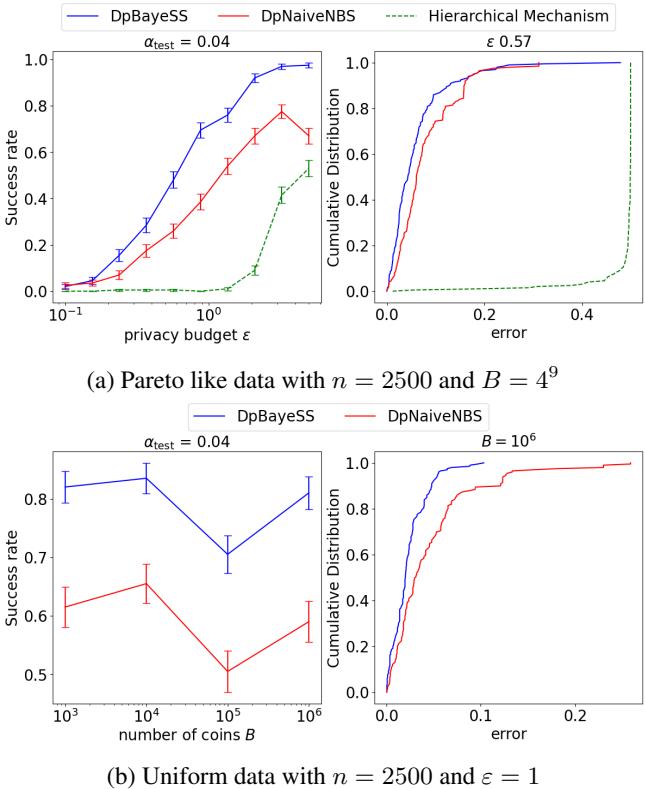
成功率 vs 硬币域大小 B。DpBayeSS (蓝色) 保持高于 Naive (红色) 。

在图 1 (上图) 中，左侧图表显示了随着定义域大小 \(B\) 从 \(10^3\) 增加到 \(10^6\)，成功率的变化。自适应 DpBayeSS (蓝色) 保持了较高的成功率，而 Naive 方法 (红色) 下降得更快。这证实了当可能值的范围很大时，自适应的“聚焦”能力至关重要。

下界: 理论极限

最后，这篇论文提出了一个基本问题: 自适应性真的必要吗? 一个巧妙的非自适应协议能否达到同样的效果？

作者证明了一个分离结果 (separation result) 。 他们通过数学推导表明，任何非自适应协议必须使用比最优自适应协议更多的用户 (多 \(\log B\) 倍) 。

他们通过将非自适应中位数问题与学习整个 CDF 的问题联系起来得出了这一结论，已知后者在样本复杂度方面更“难”。

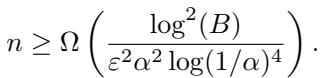
n >= Omega(log^2 B / (epsilon^2 alpha^2 log(1/alpha)^4)).

这个下界证明了他们的自适应算法所实现的效率提升不仅仅是一种改进——它们利用了交互的根本优势。

结论

《分布式隐私分位数估计的轻量级协议》中提出的研究为联邦分析迈出了重要一步。

  1. 最优性: 他们提供了一种自适应 LDP 算法，能以最优的用户数量 \(O(\log B)\) 找到中位数。
  2. 鲁棒性: 通过使用鞅论证，他们解决了“不放回采样”的实际问题，使理论上的二分查找适用于现实世界的用户池。
  3. 灵活性: 他们提供了一种洗牌 DP 变体，平衡了批处理的好处与洗牌带来的隐私放大。

对于隐私保护机器学习领域的学生和从业者来说，这凸显了一个关键教训: 交互性至关重要。 如果你的基础设施允许你顺序提问而不是一次性提问，你就可以用少得多的数据达到同样的精度——或者用同样的数据达到更高的精度——同时保持严格的隐私保证。