人多力量大: 集体如何从统计学上保证对 AI 平台的影响力

在现代数字生态系统中，用户与平台之间的关系通常被视为单行道: 平台提取数据、训练算法并主导结果。但是，当用户联合起来时会发生什么呢？

想象这样一个场景: 一群零工经济工作者希望影响算法以提高工资，或者一个消费者权益保护组织希望阻止推荐系统推广某种特定的有害产品。这就是 算法集体行动 (Algorithmic Collective Action) 的领域。

虽然操纵算法的概念 (通常被称为“数据投毒”) 并不新鲜，但以集体形式有效地进行操作涉及巨大的风险。如果你为了抗议而修改了你的数据，但算法却忽略了你，那么你付出代价却一无所获。为了让集体行动变得可行，群体需要一种方法在行动 之前 从数学上预测他们的成功率。

在这篇文章中，我们将剖析一篇引人入胜的论文 “Statistical Collusion by Collectives on Learning Platforms” (学习平台上的集体统计共谋) 。 研究人员开发了一个统计框架，使集体能够估算出他们可以对学习算法施加的确切影响力，从而有效地将数据投毒从一种暗黑艺术转变为一门可计算的科学。

核心问题: 风险与不确定性

当平台训练机器学习模型时，它依赖于大数定律。它假设个人用户是独立的，并且他们的数据反映了“基本事实 (ground truth) ”。集体通过协调他们的行为打破了这一假设。

先前的研究 (如 Hardt et al., 2023) 已经确定，如果一个群体足够大，他们确实可以控制平台。然而，该研究基于“无限数据”的假设——一个理想化的世界，在这个世界里我们知道所有事物的确切概率分布。

在现实世界中，集体拥有的数据是 有限的 。 他们不知道平台算法的确切内部运作方式，也不知道其余人口的确切构成。他们只有其成员汇集的数据。

本文的目标就是弥合这一鸿沟。研究人员提出的问题是: 一个集体如何利用自身有限的数据来设计策略，并以高概率保证其成功?

设定: 平台 vs. 集体

让我们先明确这场博弈中的参与者。

  1. 平台 (The Platform) : 部署一个分类器 (如垃圾邮件过滤器、招聘机器人或产品评分系统) 。它在一个大小为 \(N\) 的数据集上进行训练。它试图根据所看到的数据最小化误差。
  2. 人群 (The Population) : 普通用户和集体的混合体。
  3. 集体 (The Collective) : 一个大小为 \(n\) (其中 \(n < N\)) 的群体。他们希望使用策略函数 \(h\) 修改他们的数据点 \((x, y)\) 以实现特定目标。

平台看到的是普通用户的“干净”数据和集体的“被修改”数据的混合。然后，它根据这种混合分布更新其分类器 \(\hat{f}\)。

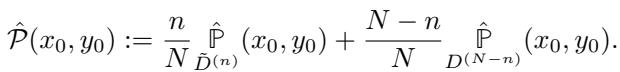
描述平台观察到的混合分布的公式。

这里，\(\hat{\mathcal{P}}\) 是平台看到的分布。它是集体修改后的数据 (\(\tilde{D}^{(n)}\)) 和普通用户数据 (\(D^{(N-n)}\)) 的加权平均值。

集体的力量在于比率 \(n/N\)。如果他们占用户群的 0.01%，他们就是噪音。如果他们占 10%，他们可能就是信号。挑战在于确定临界点究竟在哪里。

工具箱: 统计集中性

为了在不知道完整总体分布的情况下预测成功，集体依赖于 霍夫丁不等式 (Hoeffding’s Inequality) 。

简单来说，霍夫丁不等式允许我们界定观察到的平均值 (来自集体的数据) 与真实总体平均值之间的误差。研究人员定义了一个误差项 \(R_\delta(k)\)，它随着数据量 \(k\) 的增加而收缩。

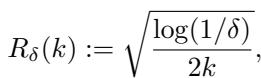
霍夫丁误差项 R_delta 的定义。

这个小小的方程是本文的动力引擎。它告诉集体: “根据你拥有的 \(n\) 个成员，你对世界的估计在 \(\pm R_\delta(n)\) 的范围内是准确的。” 这个误差项使得保证具有了“统计性”——它们以高概率 (至少 \(1-\delta\)) 成立。

目标 1: 信号植入 (Signal Planting)

最直接的影响形式是 信号植入 。 集体希望平台学习一条特定的规则: “每当你看到特征 \(X\)，就预测标签 \(Y^*\)。”

例如，一群用户可能希望强迫算法将某种特定类型的汽车 (比如 SUV) 评为“差 (Poor) ”，而不管其实际的安全功能如何。

策略

集体采用 特征-标签策略 (Feature-Label Strategy) 。 对于集体的每个成员，他们将数据点修改为具有目标特征 (“信号”) 和目标标签。

\[h(x, y) = (g(x), y^*)\]

其中 \(g(x)\) 转换特征 (例如，将“轿车”更改为“SUV”) ，\(y^*\) 是期望的标签 (例如，“差”) 。

保证

他们怎么知道这是否有效？研究人员推导出了 成功率下界 (Lower Bound on Success) 。 这个不等式允许集体代入他们的数字，看看他们是否会赢。

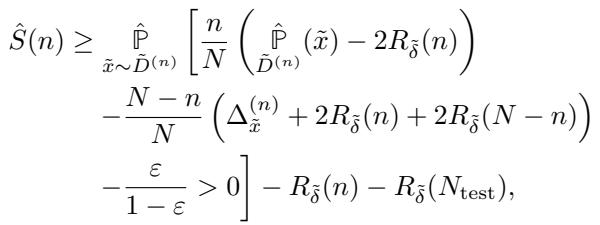
信号植入成功的下界不等式。

这个公式看起来可能很吓人，但让我们把它分解成一个关于 影响力 vs. 阻力 的故事:

  1. 集体的推动 (第一项) : \(\frac{n}{N} (\dots)\)。这代表了集体的力量。它随群体规模 (\(n\)) 扩展。有效植入信号的成员越多，这个值就越高。
  2. 人群的阻力 (第二项) : \(- \frac{N-n}{N} (\dots)\)。这代表了“干净”数据的反击。如果其余人群强烈地将该信号与 不同的 标签联系起来，这一项就会很大，从而使成功变得更加困难。
  3. “安全边际” (\(R_\delta\) 项) : 注意 \(R_\delta\) 项前的减号。因为集体依赖于有限的样本，他们必须保守。他们减去潜在的统计误差，以确保他们的预测在最坏的情况下也能成立。

如果这个方程的结果大于 0，集体实际上就“赢了”——平台很可能会采纳植入的规则。

仅特征策略 (Feature-Only Strategy)

有时，用户无法更改标签 (例如，在贷款申请中，结果“违约”或“已偿还”可能是固定的) 。他们只能更改他们的特征。论文为此提供了一个修正后的界限，尽管它自然要弱一些，因为集体的杠杆作用较小。

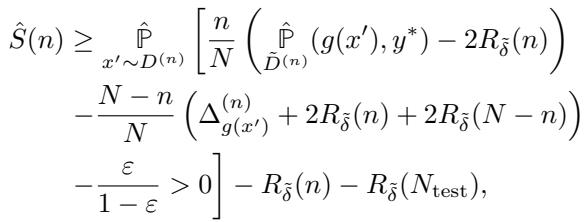
仅特征策略的下界不等式。

目标 2: 信号移除 (Signal Unplanting)

有时目标不是强迫产生特定的结果，而是 打破 现有的关联。这就是 信号移除 。

想象一个算法不公平地将特定的邮政编码与“高信用风险”联系起来。集体不一定想强行贴上“低风险”的标签 (这可能看起来很可疑) ；他们只是想阻止算法默认判定为“高风险”。

“朴素” vs. “自适应”策略

一种朴素的方法是只刷单一的、不同的标签。但一种更聪明的 自适应策略 (adaptive strategy) 会给模型制造更多的混乱。

集体将其成员分开。它使用一个小型的子小组 (\(n_e\)) 来分析数据并估计: 除了我们要隐藏的那个标签之外，最可能的标签是什么？

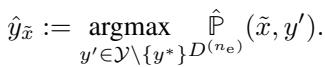
估计最佳替代标签的公式。

一旦他们确定了这个“次优”标签 (\(\hat{y}\)) ，其余的集体成员就将他们的数据切换到该标签。

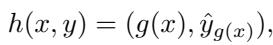
自适应移除策略函数。

这很聪明，因为它利用了数据的自然分布。它将模型推向一个原本就合理的结论，使得“移除”比试图强加一个完全不自然的标签要有效得多。

目标 3: 信号擦除 (Signal Erasing)

最后的目标是最微妙的: 信号擦除 。 在这里，集体希望平台对某种变化变得 具有不变性。如果我在照片中改变了发色，面部识别系统应该仍然能认出我。如果系统对某种变化存在偏见，集体就会采取行动擦除这种偏见。

目标是确保模型对修改后的特征 \(g(x)\) 的预测与对原始特征 \(x\) 的预测相同。

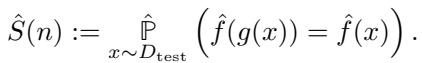
信号擦除成功的数学定义。

为了实现这一目标，集体实际上是在“填补空白”。他们观察修改后特征的标签分布，并策略性地注入数据，使条件概率分布看起来与原始特征完全相同。这需要大得多的集体规模，因为估计完整的分布 (以匹配它) 在统计成本上很高。

实验结果: 影响力的“阶梯”

研究人员使用合成的汽车评估数据集验证了这些界限。他们模拟了一个试图影响汽车评级平台的集体。结果揭示了影响力扩展的独特模式。

1. S型曲线与阶梯

在先前研究的无限数据极限中，影响力曲线看起来像平滑的 Sigmoid (S型) 函数。然而，对于有限的离散数据，研究人员发现了一种 阶梯状模式 。

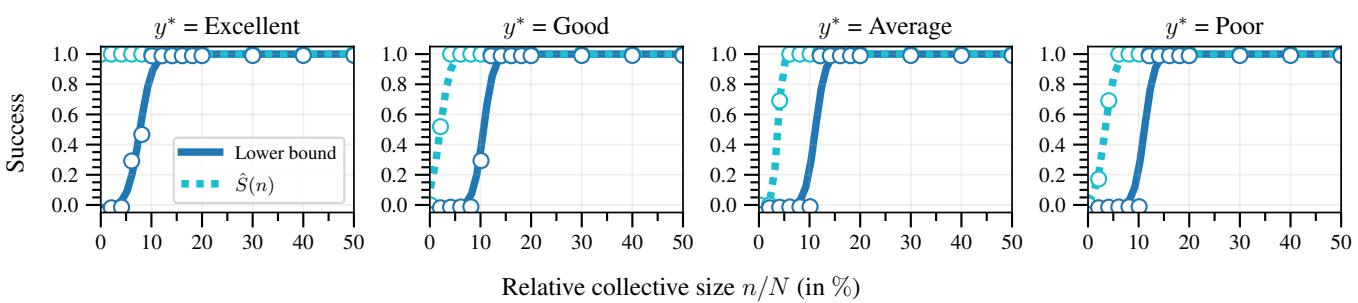
图 1 展示了信号植入的理论下界与真实成功率之间的比较。

看上面的图。

  • 虚线 (\(\hat{S}(n)\)): 这是实际的成功率。注意它在一段时间内保持为 0，然后突然上升。这表明小型集体几乎 没有 影响力，直到他们达到一个“临界点”，在那里他们克服了人群的阻力。
  • 实线 (下界) : 这是集体计算出的保守估计。它紧密跟踪真实的成功率，但保持在略低的位置。这证明了该框架是有效的: 集体可以安全地信任这个计算结果。

2. 绝对规模很重要

本文最深刻的见解之一是 相对规模 (\(n/N\)) 是不够的 。

如果一个集体代表了 10% 的人口，他们强大吗？

  • 如果 \(N=1,000\) 且 \(n=100\)，他们的统计误差 (\(R_\delta\)) 很高。他们的估计是模糊的。
  • 如果 \(N=1,000,000\) 且 \(n=100,000\)，他们的误差极小。

大型平台实际上对集体行动 更脆弱 , 因为集体行动具有更高的统计精度。

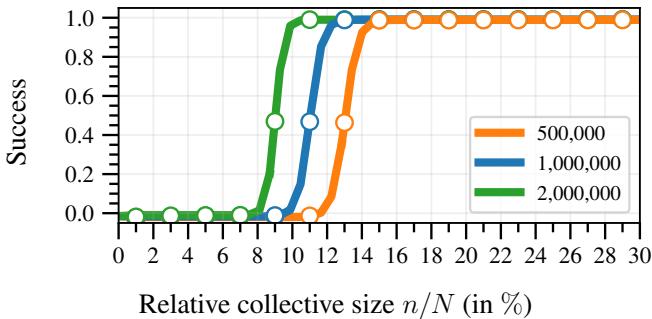
图 2 展示了增加总人口 N 如何收紧下界。

在图 2 中，你可以看到对于相同的相对百分比 (X轴) ，随着 \(N\) 的增加，曲线变得更陡峭并向左移动 (绿线 vs. 橙线) 。在大型平台上拥有 100,000 名用户的集体，比在小型平台上拥有 100 名用户的集体更有效，即使他们都占用户群的 10%。

3. 自适应移除策略胜出

实验还表明，用于移除信号的 自适应策略 (估计次优标签) 大大优于朴素策略。

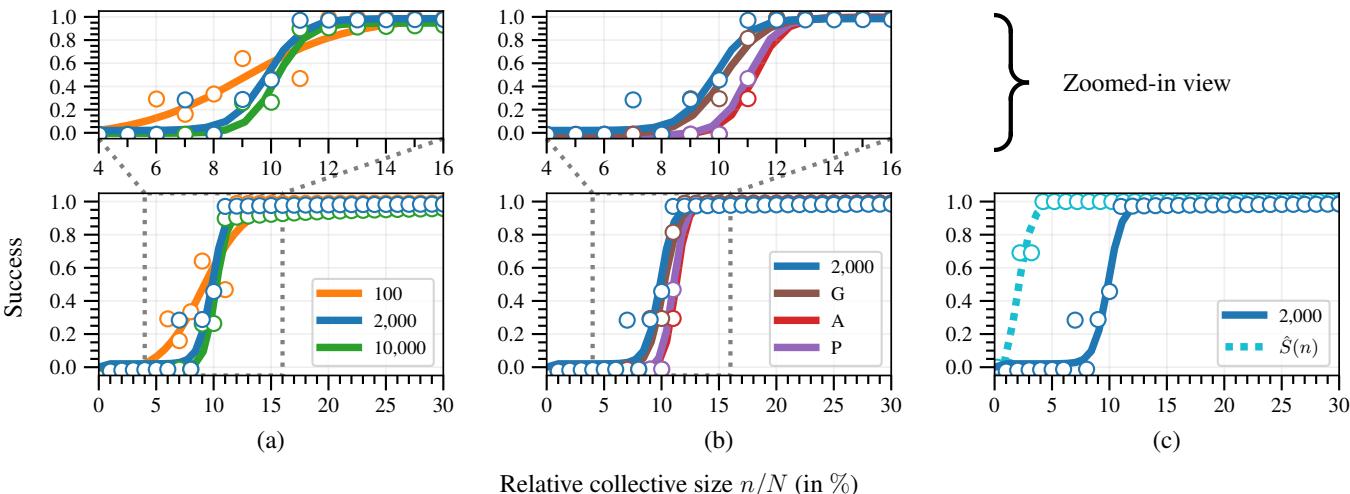
图 3 展示了信号移除的结果。

在图 3(b) 中，自适应策略 (蓝色) 比朴素策略 (盲目植入“好”、“中”或“差”) 以更小的集体规模取得了成功。图 3(a) 也强调了权衡: 如果你用太多的成员来 估计 策略 (\(n_e\)) ，你就没有足够的成员来 执行 它。这里存在一个最佳平衡点。

结论: 数字工会的未来

这项研究改变了对抗性机器学习的叙事。它从恶意黑客的“攻击”概念转向了协调用户的“谈判”概念。

通过提供一个统计框架，作者表明集体不需要盲目行事。他们可以:

  1. 汇集他们的数据。
  2. 计算他们想要改变的特征的具体“阻力”。
  3. 计算克服该阻力所需的确切成员数量。
  4. 以统计上的成功保证执行行动。

其影响是深远的。随着平台变得越来越大，它们在统计上变得更加稳定，但也更容易受到能够高精度估计平台行为的大型协调群体的攻击。这篇论文为未来的数字工会提供了数学蓝图。