Transformer 架构无疑彻底改变了深度学习。从 GPT-4 这样的大语言模型 (LLM) 到视觉模型，“Attention is All You Need” (注意力即一切) 的范式无处不在。然而，尽管它们取得了巨大的成功，我们在理解它们为何如此有效方面仍在努力追赶。一个专为机器翻译设计的机制，是如何变成通用的上下文学习器的？

目前最引人注目的一种理论将 Transformer 与联想记忆 (Associative Memory) ——特别是密集联想记忆 (DAM) 或现代 Hopfield 网络——联系在了一起。该观点认为，注意力机制不仅仅是“关注”序列的某些部分；它实际上是在执行能量最小化步骤以检索记忆。

在这篇文章中，我们将深入探讨 Smart、Bietti 和 Sengupta 的一篇论文，该论文完善了这一联系。他们引入了一个名为上下文去噪 (In-Context Denoising) 的框架。他们的发现既优雅又令人惊讶: 他们在数学和实证上证明了，单层 Transformer 可以充当贝叶斯最优去噪器，并且注意力操作恰好对应于特定能量景观上的单步梯度下降。

如果你是机器学习或物理学专业的学生，这篇论文架起了统计推断、深度学习架构和基于能量的模型之间的桥梁。

1. 设置: 什么是上下文去噪？

为了理解 Transformer 在做什么，作者将问题剥离到最基础的层面。与其预测莎士比亚十四行诗的下一个单词，不如让我们看一个基本的信号处理任务: 去噪 。

在标准的上下文学习 (ICL) 中，模型会被赋予一系列示例，并被要求预测新查询的输出。作者将其推广到无监督设置。

问题公式化

想象一个提示 (prompt) ，它由一系列从某个数据分布中抽取的“干净” Token \(X_1, \dots, X_L\) 组成。在序列的末尾，我们附加一个“查询” Token \(\tilde{X}\)，它是干净 Token \(X_{L+1}\) 的噪声腐蚀版本。

模型的目标很简单: 观察上下文 (干净的 Token) ，观察带噪声的查询，并预测原始的干净 Token \(X_{L+1}\)。

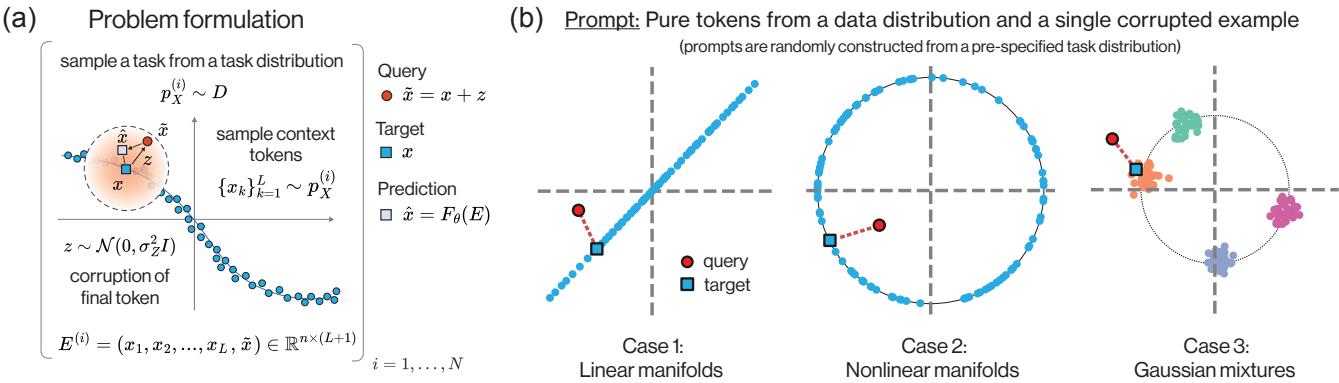
通用的上下文去噪任务的问题公式化。

如上图 Figure 1 所示，输入 \(E^{(i)}\) 包含干净的上下文和带噪声的查询。模型必须输出该查询的干净版本。

从数学上讲，目标是最小化模型预测与真实值之间的预期损失 (通常是均方误差) :

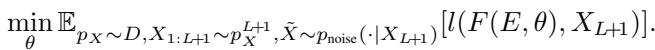
最小化目标方程。

这为何如此有趣？因为如果噪声是随机的，模型就不能简单地“死记硬背”答案。它必须观察上下文以理解数据分布的底层结构 (流形) ，然后将带噪声的查询投影到该结构上。

三个任务

作者在三种特定类型的数据分布上测试了这一点，代表了高维数据中常见的几何结构:

  1. 线性流形 (Linear Manifolds) : 数据点位于随机的低维子空间 (直线或平面) 上。
  2. 非线性流形 (Nonlinear Manifolds) : 数据点位于球面上。
  3. 高斯混合 (Gaussian Mixtures) : 数据点形成明显的聚类。

对于每个任务，上下文 Token 定义了该提示的特定几何形状 (例如，这条特定的线，或这些特定的聚类中心) 。模型必须学习去噪算法，以处理上下文中给出的任何线条或聚类排列。

2. 黄金标准: 贝叶斯最优去噪

在训练任何神经网络之前，我们需要一个基准。理论上“最好的”答案是什么？在统计学中，这就是贝叶斯最优 (Bayes Optimal) 预测器。对于均方误差损失，最优预测器是后验均值 (posterior mean) ——即在给定带噪观测值 \(\tilde{X}\) 和上下文的情况下，干净数据 \(X\) 的期望值。

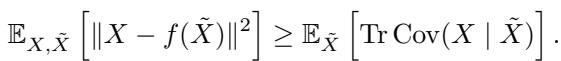
后验均值不等式方程。

作者推导出了上述三个任务的贝叶斯最优预测器的精确解析形式。这至关重要，因为它为我们提供了一个数学目标，用来与 Transformer 的行为进行对比。

线性情况: “收缩”投影

如果数据位于线性子空间 (如 3D 空间中的平面) 上，而你有一个平面外的噪点，最好的猜测是将该点正交投影到平面上。然而，由于存在噪声，我们也必须考虑不确定性。最优解是一个收缩投影 (shrunk projection) : 你投影该点，但也根据信噪比对其进行轻微缩放。

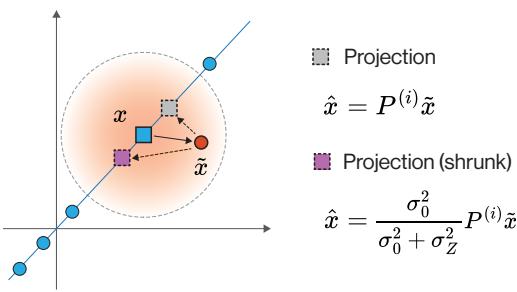
线性流形的基线估计器。

如 Figure 2 所示，投影 \(P^{(i)}\tilde{x}\) (灰色框) 将点放在线上。贝叶斯最优解 (紫色框) 将其缩放了一个因子 \(\frac{\sigma_0^2}{\sigma_0^2 + \sigma_Z^2}\)。

非线性与聚类情况

在非线性流形 (球面) 或聚类的情况下，事情变得有趣起来。最优答案不再是一个简单的矩阵投影，而是采取了上下文点的加权平均形式。

对于聚类情况 (高斯混合) ，最优预测器如下所示:

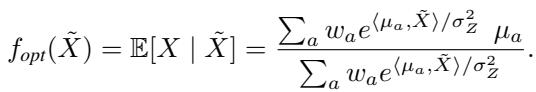
高斯混合模型的贝叶斯最优预测器。

仔细看那个方程。它根据点积 \(\langle \mu_a, \tilde{X} \rangle\) 的指数为每个分量计算一个权重，然后计算加权和。

这看着眼熟吗? 确实应该眼熟。这看起来极其类似 Transformer 中的 Softmax 注意力 (Softmax Attention) 机制。

3. Transformer 的解决方案

既然我们知道了数学上的理想情况，让我们来看看架构。作者研究了一个带有单个注意力头的单层 Transformer 。

标准 Softmax 注意力层预测输出 \(\hat{X}\) 的方程为:

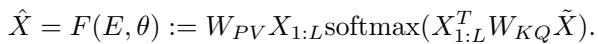
Softmax 注意力方程。

这里:

  • \(X_{1:L}\) 是上下文 Token (充当 Value \(V\) 和 Key \(K\)) 。
  • \(\tilde{X}\) 是查询 (充当 Query \(Q\)) 。
  • \(W_{PV}\) 和 \(W_{KQ}\) 是可学习的权重矩阵。

“顿悟”时刻

比较上面的 Transformer 方程和之前推导出的聚类/球面情况的贝叶斯最优解:

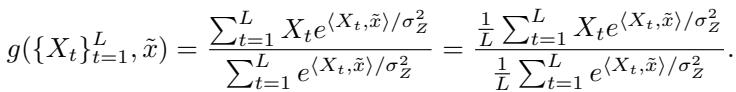
比较贝叶斯最优形式的方程。

结构是完全相同的。

  • 贝叶斯解使用 \(e^{\langle X_t, \tilde{x} \rangle / \sigma_Z^2}\) 计算权重。
  • Transformer 使用 \(\text{softmax}(X_t^T W_{KQ} \tilde{x})\) 计算权重。

如果 Transformer 将其权重矩阵 \(W_{KQ}\) 和 \(W_{PV}\) 设置为缩放的单位矩阵 , 它就能精确地恢复贝叶斯最优估计器。具体来说，即 \(W_{KQ} \approx \frac{1}{\sigma_Z^2} I\) 且 \(W_{PV} \approx I\)。

实证验证: 它们真的能学到这个吗？

理论很美好，但一个随机初始化的 Transformer 真的能通过梯度下降学会成为贝叶斯最优去噪器吗？

作者在三个任务上训练了单层 Transformer。结果显示在 Figure 3 中。

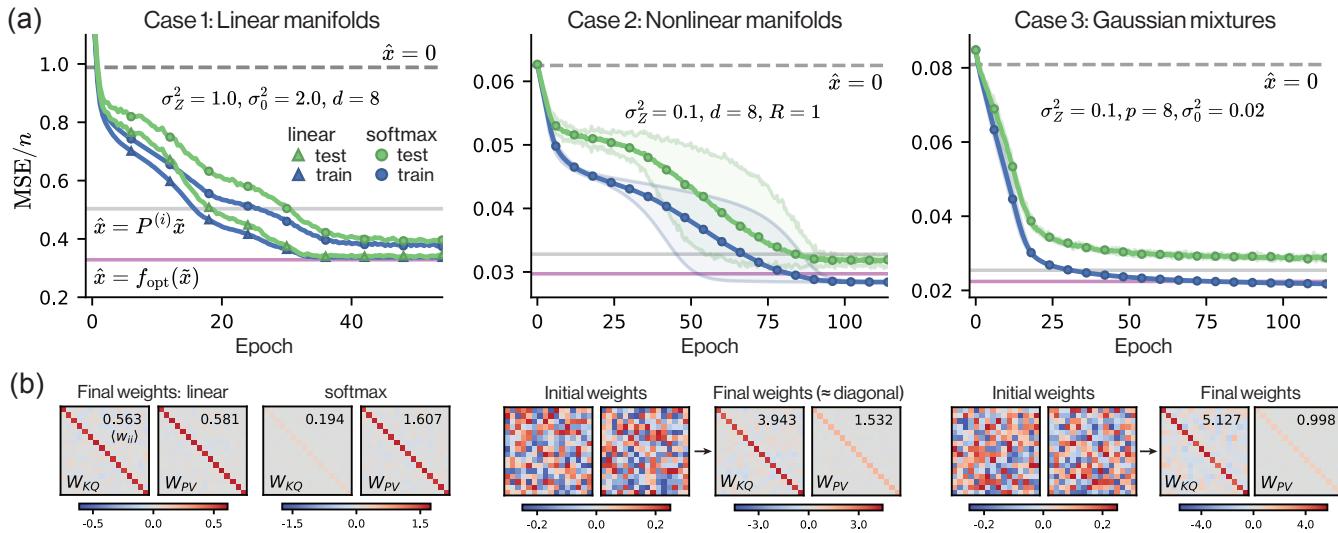
训练动态和学习到的权重。

图 (a) 显示了损失曲线。粉色线是理论上的贝叶斯最优损失。圆圈 (Softmax 注意力) 几乎完美地收敛到了这条最优线。

图 (b) 显示了学习到的权重。这是确凿的证据。矩阵 \(W_{KQ}\) 和 \(W_{PV}\) 不是杂乱无章的数字，它们是对角矩阵 。 对于线性情况，它们的乘积收敛于理论缩放因子。对于非线性情况，它们接近贝叶斯最优公式所需的单位矩阵结构。

这证实了对于这些去噪任务，单个自注意力层自然演变成了最优统计估计器。

鲁棒性与上下文长度

作者进一步探索了这个学习到的估计器有多“聪明”。随着上下文变多，它会变得更好吗？

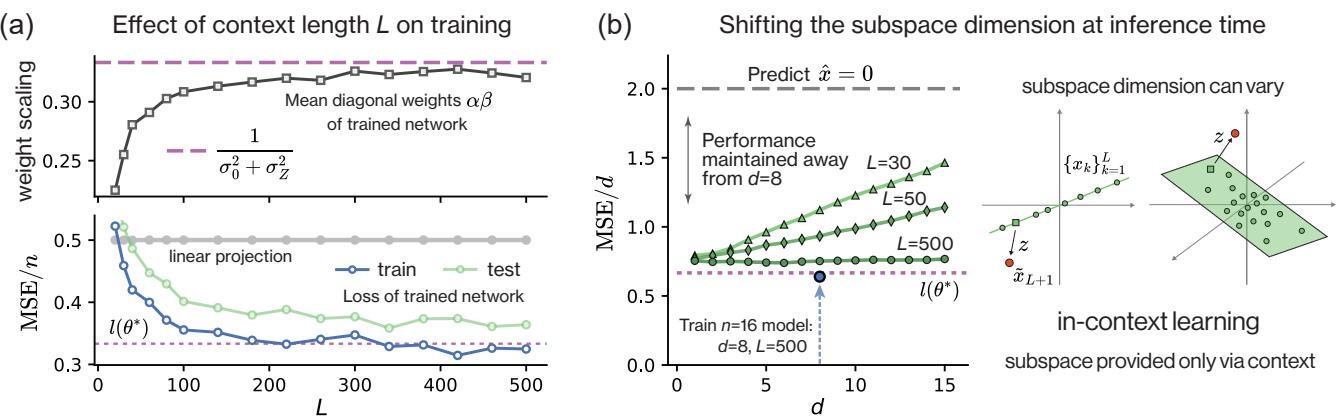
上下文长度的收敛性。

Figure 4(a) 显示，随着上下文长度 \(L\) 的增加，训练网络的权重 (方块) 和性能 (三角形/圆圈) 渐近趋向于理论最优值。

此外, Figure 4(b) 展示了关于上下文学习 (In-Context Learning) 的一个非凡之处。一个被训练用于去噪 8 维子空间的模型，在推理时可以成功地对不同维度的子空间进行去噪，只要它有足够的上下文 Token 来识别该子空间。模型不仅仅记住了“8 维子空间”，它还学会了投影的算法。

4. 物理学联系: 密集联想记忆

我们已经确定 Transformer 充当了贝叶斯去噪器。现在，让我们将其与论文的第二个主要贡献联系起来: 联想记忆 (Associative Memory) 。

经典的 Hopfield 网络将记忆存储为能量景观中的不动点 (极小值) 。要检索记忆，你从一个噪声模式开始，在能量景观上迭代地“下坡”，直到你击中一个记忆。

现代 Hopfield 网络 (密集联想记忆) 使用更陡峭的能量函数 (通常涉及指数) ，从而大幅增加了存储容量。

上下文感知能量景观

作者基于上下文 Token \(X_{1:L}\) 和状态向量 \(s\) 定义了一个特定的能量函数 \(\mathcal{E}\):

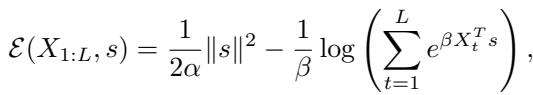
能量函数方程。

这个能量函数有两部分:

  1. 一个二次项 \(\frac{1}{2\alpha}\|s\|^2\) (保持状态有界) 。
  2. 一个 Log-Sum-Exp 项 (“现代 Hopfield”项) ，将状态拉向上下文 Token。

注意力 = 单步梯度下降

如果我们对这个能量函数关于 \(s\) 求梯度，并执行单步梯度下降 (GD) 更新，我们会得到什么？

让我们看看论文中推导出的更新规则:

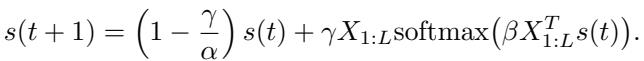
梯度下降更新规则。

如果我们将状态 \(s(0)\) 初始化为我们的噪声查询 \(\tilde{x}\) 并设置步长 \(\gamma = \alpha\)，第一项 \((1 - \frac{\gamma}{\alpha})s(t)\) 就消失了。我们剩下:

\[ s(1) = \alpha X_{1:L} \text{softmax}(\beta X_{1:L}^T \tilde{x}) \]

这正是我们要找的注意力层方程！

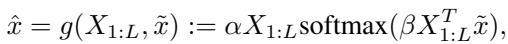
注意力方程的比较。

为什么只是一步？

标准的 Hopfield 网络通常迭代直到收敛 (许多步) 。为什么 Transformer 只做一步？

论文认为，对于去噪 , 你不希望收敛到单个记忆。如果你有一个噪声输入，收敛到最近的记忆 (一个“硬”决策) 可能是错误的。 贝叶斯最优策略是找到后验均值——即可能记忆的加权混合。

作者在 Figure 5 中精美地展示了这一点。

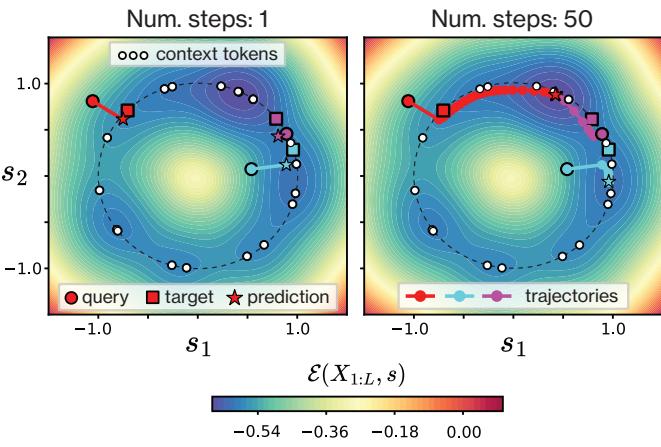
能量景观可视化。

  • 左图: 显示了 1 步后的结果 (注意力) 。星星 (预测) 从红圆圈 (查询) 向上下文 Token 簇移动，正好落在目标 (方块) 上。它找到了加权中心。
  • 右图: 显示了如果你继续迭代 (标准 Hopfield 检索) 会发生什么。点漂移到能量井的更深处，有效地“吸附”到特定的上下文 Token 上。虽然这对精确检索很有用，但这实际上对去噪来说更糟，因为它忽略了上下文分布所代表的不确定性。

这提供了一个强有力的直觉: 单个注意力层构建了一个依赖于上下文的能量景观，并沿着梯度采取一个最优步骤来估计后验均值。

5. 分析损失景观

为了进一步确认 Transformer 确实找到了这个特定的解，作者分析了训练目标的损失景观。通过将权重固定为缩放的单位矩阵 (\(\alpha I\) 和 \(\beta I\)) ，他们绘制了均方误差 (MSE) 作为 \(\alpha\) 和 \(\beta\) 的函数图像。

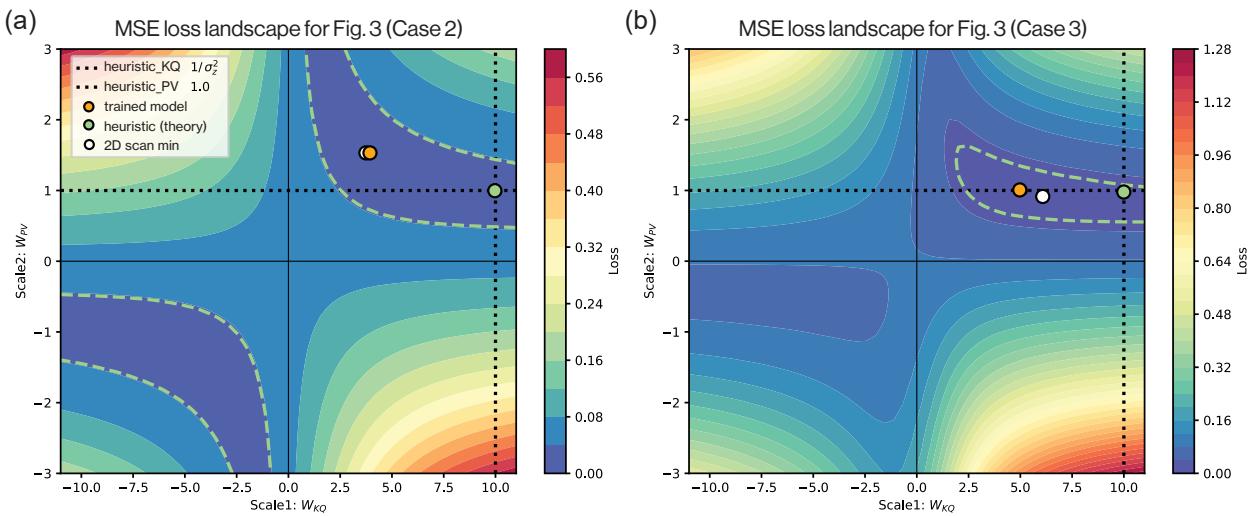
损失景观可视化。

Figure 6 展示了这些景观。

  • 绿点是理论上的贝叶斯最优设置。
  • 橙点是训练好的 Transformer 最终所在的位置。
  • 白点是景观的数值最小值。

注意它们都位于同一个低损失的“山谷”中。蓝色山谷宽阔的双曲线形状表明 \(\alpha\) 和 \(\beta\) 之间存在关系 (乘法权衡) 。这解释了为什么模型能可靠地找到解: 最优解的“吸引域 (basin of attraction) ”非常巨大。

6. 进阶: 扭曲的几何结构

最后，作者提出了一个问题: 如果世界不是各向同性的呢？如果数据被某个变换矩阵 \(A\) 拉伸或旋转了怎么办？

\[ E = (AX_{1:L}, A\tilde{x}) \]

在这种情况下，简单的单位矩阵权重就不起作用了。最优权重需要编码变换的几何结构:

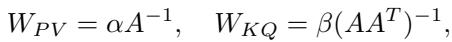
结构化权重方程。

权重 \(W_{PV}\) 和 \(W_{KQ}\) 应该变为变换相关矩阵的逆矩阵。

值得注意的是，单层 Transformer 也能学会这一点。

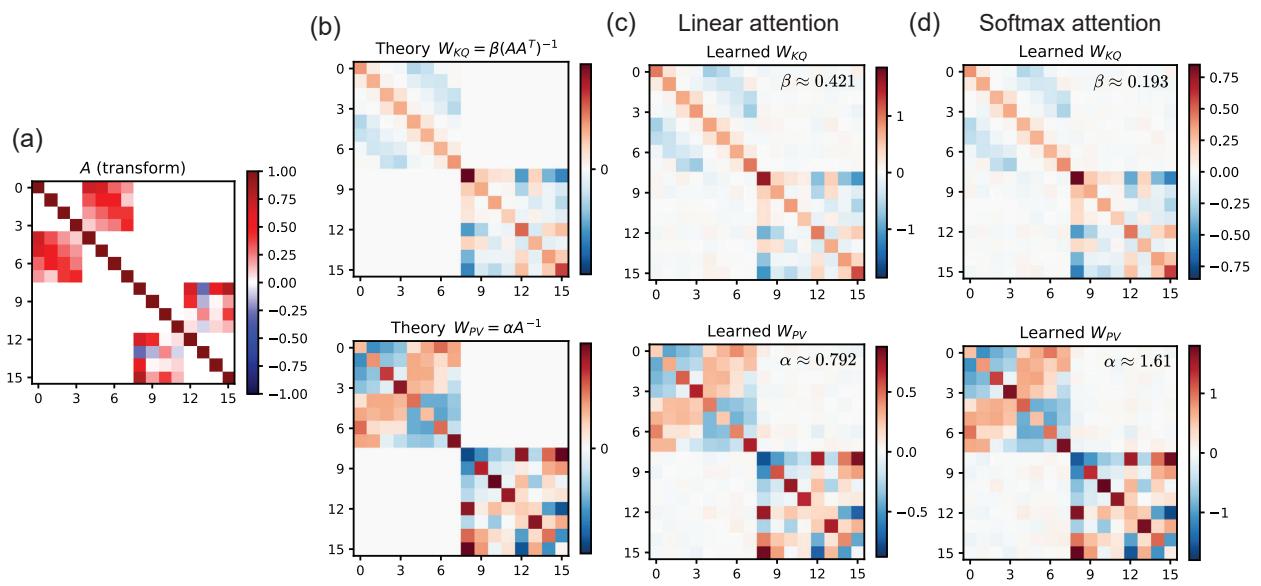
结构化权重可视化。

在 Figure 8 中:

  • 图 (a) 显示了变换矩阵 \(A\)。
  • 图 (b) 显示了理论上的最优权重 (结构化的，非对角的) 。
  • 图 (c) 和 (d) 分别显示了线性注意力和 Softmax 注意力层实际学到的权重。它们恢复了撤销变换 \(A\) 所需的复杂结构。

这证明了 Transformer 不仅仅是在对附近的点进行平均；它还在学习执行平均操作所在的度量空间。

结论

Smart 等人的这篇论文为 Transformer、贝叶斯推断和联想记忆提供了一个严谨、统一的视角。

以下是关键要点:

  1. Transformer 是去噪器: 自注意力机制的一个基本能力是上下文去噪。
  2. 最优性: 单层足以实现线性流形和球面流形的贝叶斯最优估计器。
  3. 机制: 学习到的权重自然收敛到实现此最优估计的配置 (缩放的单位矩阵) 。
  4. 能量解释: 注意力操作在数学上等同于在上下文定义的能量景观上进行单步梯度下降。查询初始化了下降过程，而单步更新将其移动到后验均值。

这项工作有助于揭开“黑盒”的神秘面纱。当 Transformer 处理提示词时，它不仅仅是在匹配模式；它是在根据上下文动态构建能量景观，并执行推断步骤以找到最可能的补全。它架起了向量空间中干净、几何的世界与深度学习中混乱、高维的现实之间的桥梁。