如果你在过去十年中一直关注深度学习的发展轨迹，你可能对 Rich Sutton 的文章《苦涩的教训》 (The Bitter Lesson) 并不陌生。其核心论点很简单: 从历史上看，长期以来唯一真正重要的技术就是扩大计算规模。人类的智慧——手工设计的特征或编码的领域知识——最终都会被基于海量计算训练出的庞大模型所碾压。

但是，如果我们可以利用人类知识来改进我们扩展计算的方式呢？

这就是研究论文**“Flopping for FLOPs: Leveraging Equivariance for Computational Efficiency”**背后的核心问题。作者挑战了这样一个观点: 即引入几何先验 (如对称性) 实际上会“透支”计算预算。相反，他们提出了一种构建神经网络的方法，既能尊重对称性 (特别是镜像对称性) ，又能将每个参数的浮点运算次数 (FLOPs) 削减一半。

在这篇文章中，我们将深入探讨这是如何实现的。我们将探索等变性 (Equivariance) 的数学原理，如何对线性层进行块对角化，以及如何调整像 Vision Transformers (ViT) 和 ConvNeXts 这样的现代架构，仅仅通过理解“蝴蝶在镜子中看起来还是一样的”这一事实，就能让它们运行得更快。

对称性与规模的问题

在计算机视觉中，我们知道物体通常无论方向如何都保持其身份。一只面向左边的猫与一只面向右边的猫属于同一个类别。

图 1: 常见的图像分类任务对翻转 (水平镜像) 具有不变性。在我们的实现中，这种不变性是通过等变网络层强制执行的，从而将所需的浮点运算 (FLOPs) 减半。

标准的神经网络，如普通的 ResNet 或 ViT，并不天生“知道”这一点。它们必须通过观察成千上万只面向左边的猫和成千上万只面向右边的猫来学习它。这就参数而言是低效的 (权重需要存储两种方向的信息) 。

为了解决这个问题，研究人员开发了等变神经网络 (Equivariant Neural Networks) 。 这些网络将对称性硬编码到架构中。它们保证如果你变换输入 (例如旋转或翻转它) ，内部特征会以可预测的方式进行变换。

从历史上看，这存在一个陷阱。虽然等变网络是参数高效的 (它们需要更少的权重来学习相同的任务) ，但它们通常是计算繁重的。在许多实现中，强制执行对称性需要权重共享，这会导致密集的计算。你可能在参数上节省了内存，但在 FLOPs (浮点运算次数) 和挂钟时间 (wall-clock time) 上付出了代价。

“Flopping for FLOPs” 背后的研究人员提出了一个问题: 我们能否设计一种实际上能减少计算负担的等变网络？

核心解决方案: 翻转 (Flopping) 与块对角化

本文主要解决的对称性是水平镜像，作者将其风趣地称为**“Flopping” (翻转)** 。

其直觉是停止将特征视为通用的数字，开始将其视为具有几何“类型”。当你观察神经网络中的特征图时，作者建议将通道分为两组不同的组:

  1. 不变特征 (Invariant Features, \(x_1\)) : 当输入图像被翻转时，这些特征保持不变。
  2. (-1)-等变特征 ((-1)-Equivariant Features, \(x_{-1}\)) : 当输入图像被翻转时，这些特征的符号会翻转 (乘以 -1) 。

这种看似简单的区分对于构成 Transformers 和 MLPs 计算主体的线性层 (密集矩阵乘法) 有着深远的影响。

效率的数学原理

让我们看一个标准的线性层。通常，你有一个输入向量 \(x\) 和一个权重矩阵 \(W\) 来产生输出 \(y\)。如果 \(W\) 是一个密集矩阵，每个输入都与每个输出相连。

然而，如果我们强制执行等变性，我们就在建立规则。我们希望不变输出 (\(y_1\)) 仅依赖于保持不变性的交互。

如果一个不变特征与一个 (-1)-等变特征交互，结果是 (-1)-等变的 (数学上类似于 \(正 \times 负 = 负\)) 。因此，除非权重为零，否则不变输出不能由 (-1)-等变输入形成。

这种限制迫使权重矩阵变为块对角 (block-diagonal) 形式。

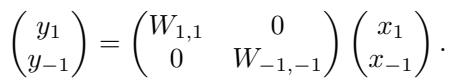
显示权重矩阵块对角分解的方程。

在上面的方程中:

  • \(W_{1,1}\) 将不变输入映射到不变输出。
  • \(W_{-1,-1}\) 将 (-1)-等变输入映射到 (-1)-等变输出。
  • 非对角块 (即将不变映射到等变，反之亦然) 必须为零 。

为什么这能节省计算量

这就是奇迹发生的地方。一个大小为 \(N \times N\) 的标准矩阵乘法大约需要 \(N^2\) 次运算。

通过将特征平均分割 (一半不变，一半等变) 并将非对角线强制为零，我们执行了两个大小为 \((N/2) \times (N/2)\) 的较小矩阵乘法。

\[ 2 \times \left( \frac{N}{2} \right)^2 = 2 \times \frac{N^2}{4} = \frac{N^2}{2} \]

我们刚刚将 FLOPs 削减了一半。

这一结果源于舒尔引理 (Schur’s Lemma) , 这是表示论中的一个基本定理。它本质上是说，不同类型的不可约表示 (irreps) 之间的线性映射必须为零。通过根据这些 irreps (对称和反对称特征) 对网络进行参数化，计算节省自然随之而来。

构建架构

如何在实践中实现这一点？我们不能仅仅将此逻辑应用于黑盒；我们需要调整现代视觉架构的具体层。

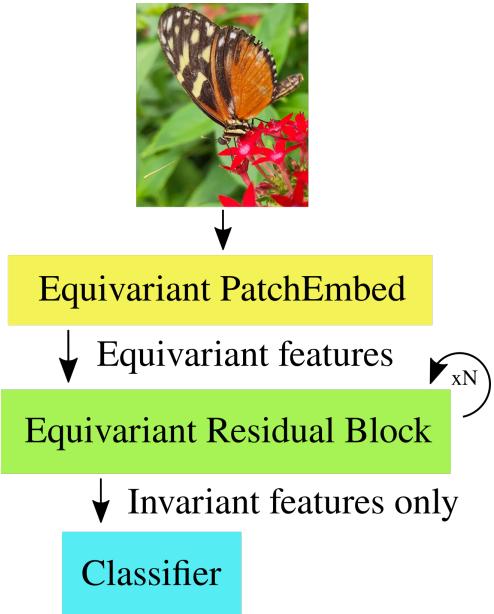
图 3: 示意图。我们的架构遵循基本的几何深度学习蓝图。

上面的示意图展示了“几何深度学习蓝图”。我们从等变嵌入开始，通过等变块处理特征，最后将它们坍缩为分类器的不变特征 (因为最终标签“猫”不应该翻转) 。

1. Patch Embedding (分块嵌入)

一切始于输入图像。为了进入我们的等变流程，我们需要将原始 RGB 像素转换为我们的两种特征类型: 不变特征和 (-1)-等变特征。

我们使用修改后的 Patch Embedding 层来做到这一点。

图 2: Patch embedding 层示意图，显示了对称和反对称滤波器。

如图 2 所示，作者对卷积滤波器实施了约束:

  • 对称滤波器: 产生不变特征。
  • 反对称滤波器: 产生 (-1)-等变特征 (当底层补丁翻转时，它们会翻转符号) 。

这创建了特征流的初始分割。

2. 非线性激活 (GELU)

线性层很容易块对角化，但神经网络需要像 GELU 或 ReLU 这样的非线性激活函数才能发挥作用。你如何将非线性应用于应该翻转符号的特征？如果你只是对负数应用 ReLU，它会变成零，从而破坏对称性信息。

作者通过变换特征来解决这个问题。他们暂时混合不变部分 (\(x_1\)) 和等变部分 (\(x_{-1}\)) 以移动到“空间”域 (\(s\) 和 \(t\)) ，在那应用非线性，然后再变换回来。

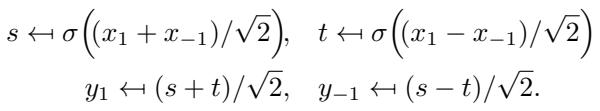
等变激活函数的方程。

虽然这看起来比标准的 GELU(x) 稍微复杂一些，但与线性层获得的节省相比，计算成本微乎其微。

3. 注意力机制 (Attention)

对于 Vision Transformers (ViT)，自注意力机制 (Self-Attention) 至关重要。作者通过将查询 (Queries, \(q\)) 和键 (Keys, \(k\)) 分割为对称和反对称部分来调整这一点。

点积 (决定注意力分数) 变为:

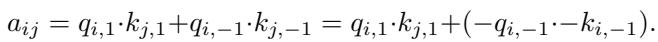
等变注意力机制的方程。

注意这一项 \((-q_{i,-1}) \cdot (-k_{j,-1})\)。因为两项都翻转符号，负号相互抵消，结果注意力分数 \(a_{ij}\) 保持不变。这确保了无论图像方向如何，注意力图都描述了补丁之间的关系。

调整现代骨干网络

作者不仅仅提出了一个理论模块；他们调整了三种最流行的计算机视觉架构: ResMLP、ViT 和 ConvNeXt 。

ResMLP

ResMLP 是一种几乎完全由线性层 (MLP) 组成的架构。由于作者的方法将线性层计算量减少了 50%，ResMLP 受益巨大。

残差块结构被修改以尊重特征分割:

显示 ResMLP 块结构的方程。

因为 ResMLP 是如此依赖密集计算，所以“Flopping”技术在这里带来了最显著的加速。

ConvNeXt

ConvNeXt 是现代化的卷积网络。ConvNeXt 中的繁重工作由深度卷积 (depthwise convolutions) 和随后的 \(1 \times 1\) 卷积 (数学上等同于线性层) 完成。

\(1 \times 1\) 卷积得到了块对角化处理 (节省 50%) 。对于深度空间卷积，作者在对称和反对称核之间交替使用。

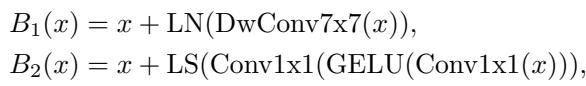
显示 ConvNeXt 块结构的方程。

虽然他们没有编写自定义 GPU 内核来完全优化深度层 (使用 Winograd 算法处理对称性) ，但在逐点层 (pointwise layers) 上的减少仍然使标准实现受益匪浅。

实验: 它有效吗？

FLOPs 的理论减少是显而易见的，但这能转化为性能吗？有时，限制网络为等变网络会迫使它学习“更差”的特征，从而降低准确性。

作者在 ImageNet-1K 上测试了他们的等变模型 (\(\mathcal{E}\)) 与标准基线的对比。

FLOPs 与参数

首先，让我们看看缩放属性。

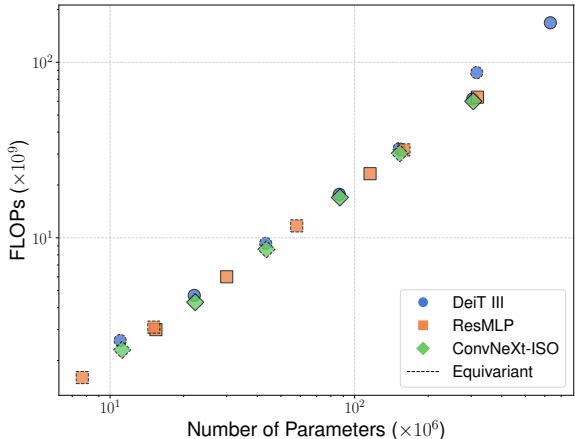
图 4: FLOPs 按模型大小缩放。比较 FLOPs 数量与模型中的参数数量。

在标准网络中，FLOPs 和参数通常呈线性比例。图 4 中的虚线代表等变模型。你可以看到它们在效率格局中占据了独特的位置，在保持较大模型参数数量的同时，大幅降低了计算需求。

准确率与计算量

对于任何效率论文来说，最关键的图表是准确率与计算量 (FLOPs) 之间的权衡。

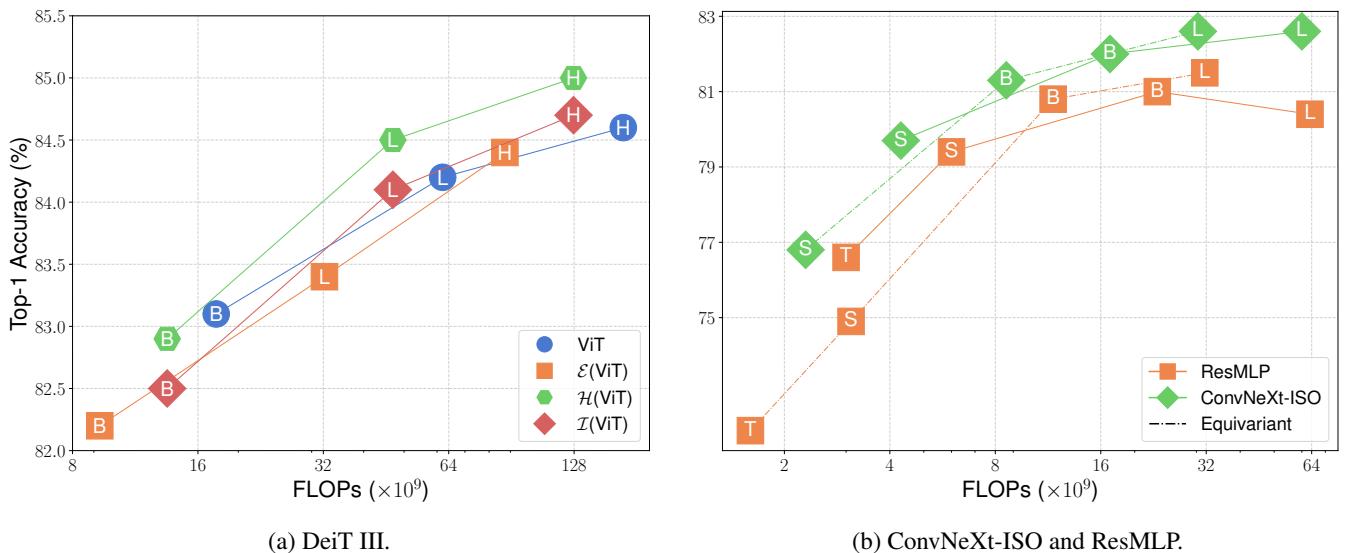
图 5: ImageNet-1K 上的验证准确率与模型复杂度的关系。

在图 5 中，查看 ConvNeXt-ISO 和 ResMLP 的图表 (底部) 。在相同的准确率下，等变模型 (黑色虚线) 始终出现在基线模型的左侧。这意味着它们以显著更少的计算量实现了可比的结果。

对于 DeiT III (ViT) (顶部图表) ，结果同样令人信服。等变版本 (\(\mathcal{E}(ViT)\)) 实现了与基线非常接近的准确率，但 FLOPs 只有基线的一小部分。例如，\(\mathcal{E}(ViT-L)\) (Large) 的计算预算大约相当于标准 ViT-B (Base) ，但实现了更高的准确率。

吞吐量 (实际速度)

FLOPs 是一个理论指标。现实世界的速度 (每秒图像数) 取决于内存带宽和 GPU 内核实现。

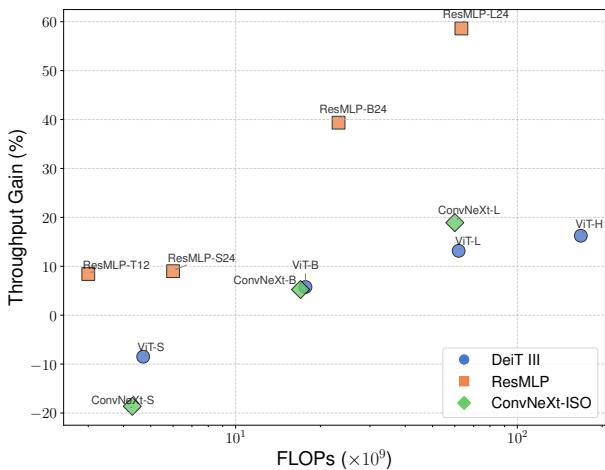
图 6: 基于模型大小的吞吐量增益。

图 6 显示了“吞吐量增益”。

  • ResMLP (橙色) : 显示出巨大的增益 (快达 60%) 。由于 ResMLP 由大型矩阵乘法主导，块对角化立即得到了回报。
  • ViT 和 ConvNeXt: 随着模型尺寸的增加，增益也在增加。对于小模型 (Small/Tiny) ，管理特征分割的开销略微超过了数学上的收益。但随着模型规模扩大 (Large/Huge) ，矩阵乘法占据主导地位，等变模型的运行速度明显快于标准模型。

关键要点

“苦涩的教训”表明我们应该停止试图耍小聪明，直接扩展计算规模。这篇论文提供了一个“甜蜜”的反驳: 在对称性上耍小聪明允许我们更有效地扩展计算。

以下是 “Flopping for FLOPs” 所取得成就的总结:

  1. 块对角效率: 通过将特征分解为不变和 (-1)-等变类型，密集线性层被拆分为两个较小的块，使 FLOPs 减半。
  2. 通用适用性: 这不仅仅适用于小众架构。它适用于 ViTs、MLPs 和 ConvNets。
  3. 可扩展性: 随着模型变大，效率增益会变得更好。这使其成为基础模型时代的一项有前途的技术。
  4. 无“对称性税”: 与以前增加计算密度的等变方法不同，这种方法在保持可比准确率的同时减少了计算密度。

通过硬编码“翻转的图像仍然是同一张图像”这一知识，我们不仅节省了模型学习这一事实的成本——我们还节省了 GPU 计算它的成本。