引言

扩散模型已经从根本上改变了生成式人工智能的版图。从 DALL-E 到 Stable Diffusion，从高斯噪声生成高保真图像的能力简直如同魔法一般。然而，标准扩散模型有一个特定的局限性: 它们通常假设从标准高斯分布 (纯噪声) 过渡到数据分布 (图像) 。

但是，如果你不想从噪声开始呢？如果你想从一个特定分布过渡到另一个特定分布呢？考虑一下图像恢复: 你想从“低质量” (LQ) 分布——模糊、有雨点或被遮挡的图像——过渡到“高质量” (HQ) 分布。这需要一种扩散桥接 (Diffusion Bridge) 。

现有的方法试图通过使用一种称为 *Doob h-变换 (Doob’s h-transform) * 的数学技术，在两个固定端点之间建立桥梁来解决这个问题。虽然在数学上是合理的，但这些方法往往过于强硬地迫使模型击中目标，导致生成的图像出现不自然的伪影、模糊或过度平滑。

UniDB 登场了，这是论文 “UniDB: A Unified Diffusion Bridge Framework via Stochastic Optimal Control” 中提出的一种新颖框架。这项研究不仅将扩散桥接视为一种统计变换，更将其重新构想为一个随机最优控制 (Stochastic Optimal Control, SOC) 问题。通过这样做，作者不仅将现有方法统一在一个理论框架下，还引入了一个“可调节”的惩罚系数，显着提高了图像质量。

在本文的深度解析中，我们将探讨 UniDB 如何利用控制理论来修复以往扩散桥接方法的缺陷，从而统一图像恢复的数学基础。

背景: 扩散桥接问题

要理解 UniDB，我们首先需要了解它所解决的局限性。标准扩散模型依赖于一个添加噪声的前向过程和一个去除噪声的反向过程。

控制前向过程的方程通常是一个随机微分方程 (SDE) :

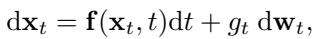
在这里，\(\mathbf{f}\) 是漂移项 (确定性的推动力) ，\(g_t\) 是扩散项 (随机噪声) 。在许多标准模型中，漂移项是线性的:

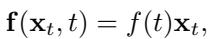
Doob h-变换的局限性

当我们想要连接两个特定的分布时 (例如，将模糊照片转换为清晰照片) ，我们需要对扩散过程进行条件化处理，使其从 \(\mathbf{x}_0\) 开始，并保证到达 \(\mathbf{x}_T\)。

历史上，研究人员使用 Doob h-变换 。 该技术修改了 SDE 的漂移项，强制路径击中特定的终端点 \(\mathbf{x}_T\)。修改后的前向过程如下所示:

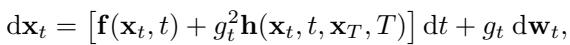
项 \(\mathbf{h}(\mathbf{x}_t, t, \mathbf{x}_T, T)\) 是添加到漂移项中的额外“力”，以确保粒子准确落在目标上。虽然这在理论上行得通，但 UniDB 的作者指出了一个关键缺陷: 它太僵化了。

通过强制轨迹精确匹配端点 (硬约束) ，模型通常不得不在状态空间中做出“不自然”的移动，导致局部模糊和失真。它缺乏为了换取更平滑、更逼真的图像轨迹而牺牲一点点端点精度的灵活性。

核心方法: 基于随机最优控制的 UniDB

UniDB 的主要贡献在于将视角从简单的概率变换转变为随机最优控制 (SOC) 。

在 SOC 中，我们扮演“控制器”的角色。我们要引导一个系统 (图像生成过程) 从起始状态到达目标状态。然而，我们需要为施加控制 (能量) 支付“代价”，如果我们错过了目标，还需要支付“惩罚”。

可视化差异

下图完美地展示了 UniDB 与传统 Doob 方法背后的直觉差异。

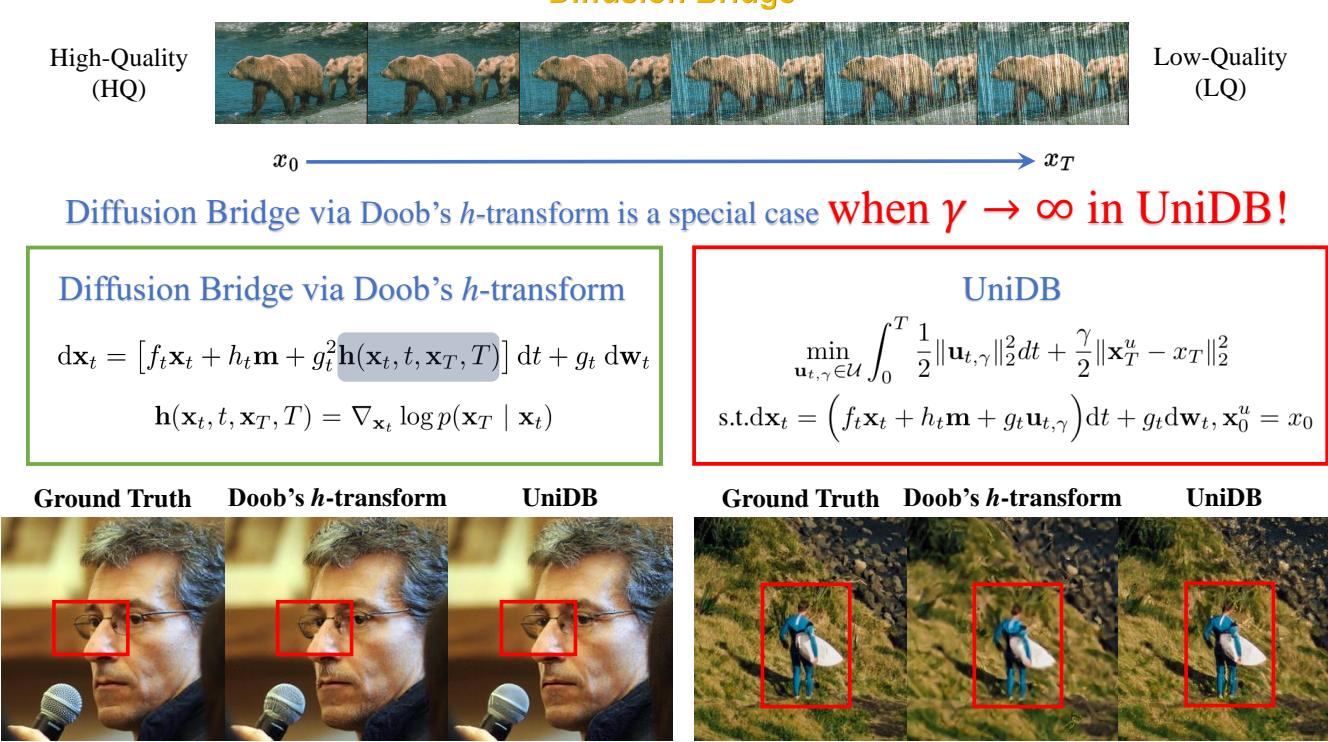
在绿色框中 (Doob h-变换) ，路径是被强制的。在红色框中 (UniDB) ，路径是经过优化的。你可以看到在图底部的示例图像中，UniDB 的输出 (红色) 恢复了细微的纹理 (如麦克风网格或草地) ，而 Doob 的方法 (绿色) 则将这些细节模糊化了。

构建优化问题

UniDB 将扩散桥接定义为一个优化问题。我们希望找到一个控制函数 \(\mathbf{u}_{t, \gamma}\)，以最小化特定的成本函数:

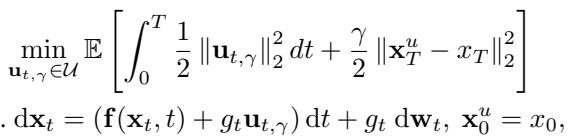
让我们拆解这个方程，因为它是论文的核心:

1. 积分项 (\(\int \frac{1}{2} \|\mathbf{u}\|^2 dt\)): 这代表“控制成本”。它实际上是在惩罚模型对图像轨迹进行剧烈、高能量的改变。我们希望路径是平滑且“容易”穿越的。
2. 终端项 (\(\frac{\gamma}{2} \|\mathbf{x}_T^u - x_T\|^2\)): 这就是“终端惩罚”。它根据最终生成的图像 \(\mathbf{x}_T^u\) 与目标真实图像 \(\mathbf{x}_T\) 之间的距离来惩罚模型。
3. 系数 \(\gamma\): 这是一个神奇的数字。它控制着权衡。高 \(\gamma\) 意味着“不惜一切代价击中目标！”低 \(\gamma\) 意味着“专注于平滑的路径，即使稍微偏离目标也没关系。”

该系统受制于以下线性 SDE:

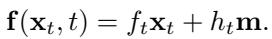
这种设置允许作者推导出最优控制器的闭式解 (closed-form solution) 。 因为系统是线性的且成本是二次的 (线性二次高斯控制问题) ，我们可以解析地求解它。

最优控制器

通过应用庞特里亚金极大值原理 (最优控制中的一个基本定理) ，作者推导出了最优控制输入 \(\mathbf{u}^*_{t, \gamma}\) 的精确公式:

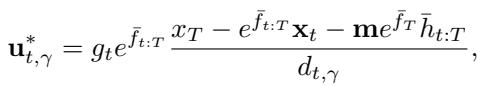
这个方程看起来可能很吓人，但它说明了一个道理。最优推动力 (\(\mathbf{u}^*\)) 取决于当前状态 \(\mathbf{x}_t\)、目标 \(\mathbf{x}_T\) 以及参数 \(\gamma\) (隐藏在项 \(d_{t, \gamma}\) 中) 。

“顿悟”时刻: 统一理论

这是论文最重要的理论贡献。作者证明了传统方法 (Doob h-变换) 实际上只是 UniDB 的一个特例 。

具体来说，如果你采用 UniDB 框架并让惩罚系数 \(\gamma\) 趋向于无穷大 (\(\gamma \to \infty\)) ，UniDB 控制器在数学上就变得与 Doob h-变换完全相同。

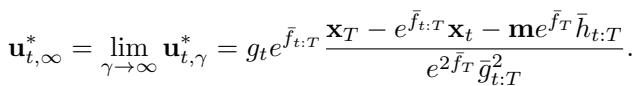
这就解释了为什么以前的方法会有质量问题。通过隐含地设置 \(\gamma = \infty\)，以前的模型实际上是在解决一个为了端点的无限严格性而忽略“控制成本” (平滑度) 的优化问题。这迫使 SDE 采取“昂贵” (不自然) 的路径来满足硬约束，从而导致了前图中看到的伪影。

作者正式提出，具有有限 \(\gamma\) 的最优控制器比无限情况产生更低的总成本 (平滑度和准确性的更好平衡) :

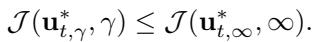
通过将 \(\gamma\) 视为一个超参数而不是一个固定的无穷大值，UniDB 获得了生成更高质量图像的灵活性。

实现: UniDB-GOU

为了验证这一理论，作者将 UniDB 应用于 广义 Ornstein-Uhlenbeck (GOU) 过程。GOUB (GOU Bridge) 是目前最先进的图像恢复方法之一。通过用 UniDB 框架升级 GOUB，他们创建了 UniDB-GOU 。

UniDB-GOU 的前向 SDE 如下所示:

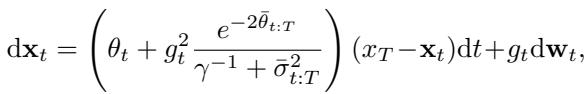
注意包含 \(\gamma^{-1}\) 的项。如果 \(\gamma \to \infty\)，则 \(\gamma^{-1} \to 0\)，这个方程就坍缩回标准的 GOUB 方程。但是有了有限的 \(\gamma\)，漂移项得到了调节，防止了在端点附近“力”变得过于极端。

训练目标

我们实际上如何训练神经网络来学习这个呢？作者推导出了一个基于转移概率的损失函数。网络预测分数 (对数密度的梯度) ，损失函数衡量“后验均值” (数学上我们应该在的地方) 与“预测均值” (网络认为我们在的地方) 之间的差异。

训练目标公式如下:

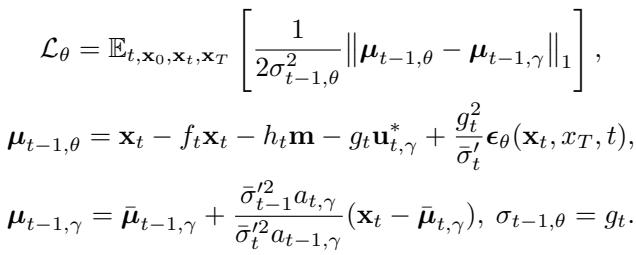
这看起来很复杂，但在功能上，它与标准的扩散训练非常相似，只是修改了系数 (\(a_{t, \gamma}\) 和 \(\bar{\mu}_{t, \gamma}\)) 以考虑控制参数 \(\gamma\)。这意味着 UniDB 可以通过极少的代码修改集成到现有的代码库中。你只需要替换掉系数公式即可。

实验与结果

研究人员在三个主要的图像恢复任务上评估了 UniDB:

1. 图像超分辨率 (将小图像放大 4 倍) 。
2. 图像去雨 (去除雨痕) 。
3. 图像修补 (填充图像的缺失部分) 。

定量分析

下表总结的结果表明，UniDB 始终优于 GOUB、IR-SDE 和 DDRM 等基线模型。

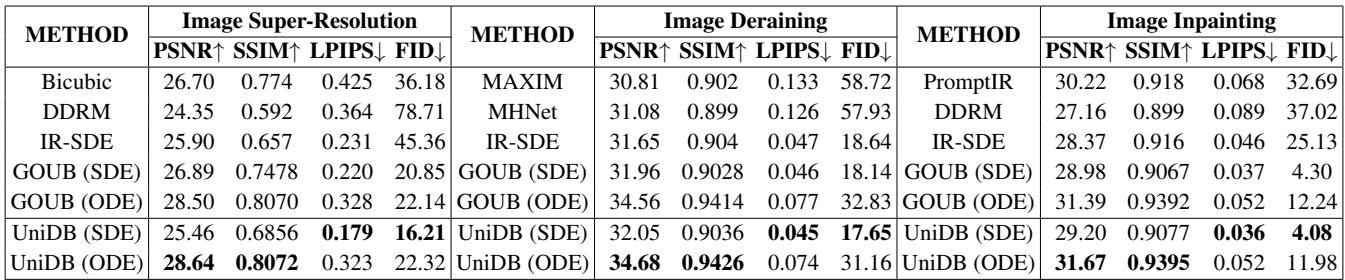
重点关注的指标:

• PSNR/SSIM: 越高越好。这些指标衡量信号保真度。UniDB 在这方面取得了最高分。
• LPIPS/FID: 越低越好。这些指标衡量感知质量 (图像对人类来说看起来有多“真实”) 。UniDB 在 FID 上显示出显著下降，表明纹理更加逼真。

视觉分析

数据虽好，但在图像生成中，眼见为实。

超分辨率 (4x)

在下图中，将“GOUB”列与“UniDB”列同“Ground Truth” (GT) 进行对比。

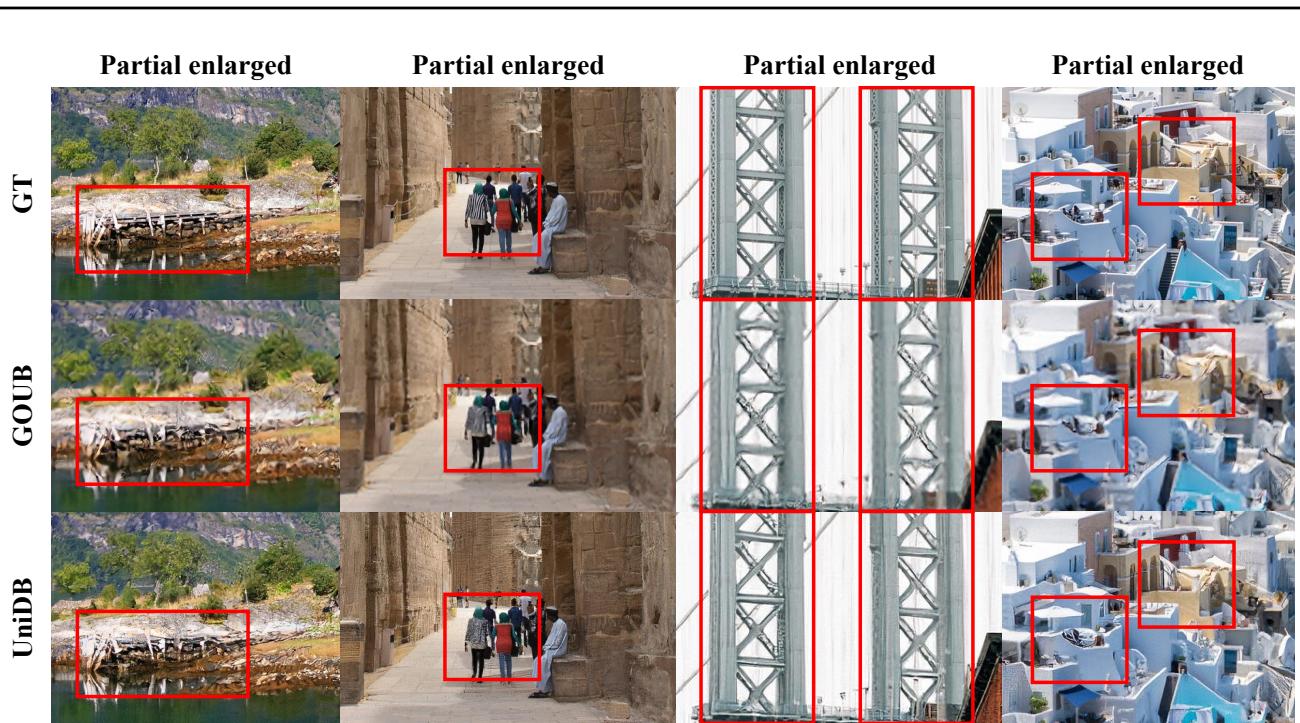
仔细观察红色的放大框。GOUB 经常让纹理变得略显浑浊或过度平滑。UniDB 恢复了清晰的边缘和特定的纹理，与 Ground Truth 更加吻合。

去雨和修补

同样的趋势也适用于去除雨水和填充面部。

在修补任务 (右侧) 中，观察面部特征。UniDB 生成的眼睛和鼻子在结构上是一致且清晰的，而以前的方法有时会产生“梦幻般”模糊的特征。

Gamma 消融实验

论文中最有趣的部分之一是对 \(\gamma\) 的分析。既然 \(\gamma\) 控制着“平滑度”和“准确性”之间的平衡，那就应该有一个“最佳点”。

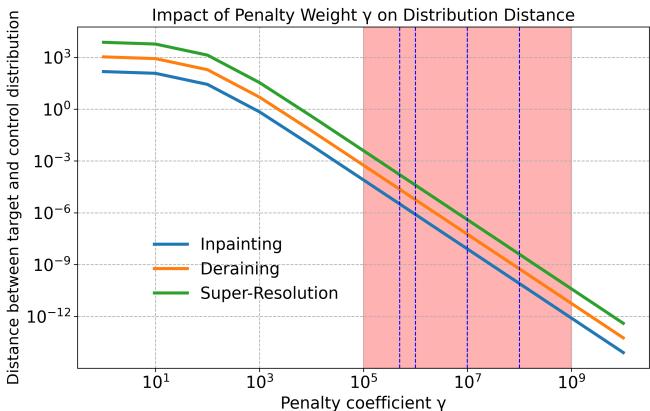
该图绘制了生成分布与目标分布之间的距离。

• 随着 \(\gamma\) 增加 (向右移动) ，距离减小 (模型更准确地击中目标) 。
• 然而，作者发现超过某一点 (大约 \(10^7\) 或 \(10^8\)) 后，感知质量 (FID) 开始下降，即使数学上距离更小了。
• “最佳点” (红色阴影区域) 代表一个有限的 \(\gamma\)，在这里模型足够准确，但保留了生成自然、高频细节的自由度。

结论与启示

UniDB 代表了对扩散桥接理论理解的重大进步。通过随机最优控制的视角重新构建问题，作者:

1. 统一了领域: 展示了 Doob h-变换和各种其他桥接模型 (VP, VE, GOU) 都是单一控制框架的特例。
2. 找出了伪影的根本原因: 将模糊和失真归因于以前方法中隐含的“无限惩罚”。
3. 提供了实用的解决方案: 引入了可调节的 \(\gamma\) 参数，通过极少的代码更改即可改善超分辨率、修补和去雨的结果。

对于学生和研究人员来说，UniDB 提供了一个有力的教训: 有时，放宽硬约束 (如精确的端点匹配) 可以带来全局更好的解决方案。通过像试图平稳飞行的飞行员那样思考，而不是像试图强制点匹配的数学家那样思考，我们可以构建更好的生成模型。

UniDB 的代码已经开源，供那些希望尝试这一新框架的人使用，它有望成为条件图像生成任务的新标准。