如果你曾经使用过 ChatGPT 或任何现代大型语言模型 (LLM) ，你就已经与自回归模型 (Autoregressive Model, ARM) 有过交互。这些模型以一种非常特定的方式生成文本: 从左到右，逐个 token (词元) 生成。它们非常成功，但也非常僵化。它们必须完全根据之前的内容来决定接下来的内容。

但是，如果“下一个”token 并不是最容易预测的那个呢？如果句子的结尾比中间更容易猜到呢？

这时就要请出掩码扩散模型 (Masked Diffusion Models, MDMs) 了。与其自回归的“表亲”不同，MDM 可以按任意顺序生成 token。它们的工作原理是逐步填充受损序列中的空白 (即“去掩码”/unmasking) 。

很长一段时间以来，人们的共识是: MDM 虽然有趣，但在语言建模方面通常不如 ARM。它们更难训练，而且往往困惑度 (perplexity) 表现更差。然而，一篇引人入胜的新论文 *“Train for the Worst, Plan for the Best” (做最坏的训练打算，做最好的推理规划) * 颠覆了这一说法。研究人员提出，正是让 MDM 难以训练的因素——缺乏固定顺序——恰恰使它们在推理时成为了更优秀的推理者。

在这篇文章中，我们将深入探讨这篇论文。我们将探索为何 MDM 面临如此残酷的训练环境，这种复杂性如何让它们能够“规划”生成策略，以及推理过程中一个简单的改变如何让它们在数独等逻辑谜题上大获全胜，并显著超越标准的自回归模型。

1. 背景: 双模型记

要理解这篇论文的贡献，我们首先需要区分离散生成建模中的两种主导范式。

僵化的专家: 自回归模型 (ARMs)

ARM 基于一个简单的原则运作: 顺序至关重要 。 具体来说，是左到右的顺序。当训练 ARM 时，它学习的是在给定历史 \(x_{0}, \dots, x_{i-1}\) 的情况下预测下一个 token \(x_i\)。

在数学上，这将序列 \(x\) 的概率分解为条件概率的乘积:

\[ p(x) = \prod_{i=1}^{L} p(x_i | x_{ 这意味着在训练期间，模型只需要解决 \(L\) 个特定的问题 (预测第 1 个 token，第 2 个，……，第 \(L\) 个) 。这种方式高效且稳定，这也是为什么像 LLaMA 和 GPT 这样的模型都采用这种构建方式。

灵活的通才: 掩码扩散模型 (MDMs)

MDM 采取了不同的方法。它们被训练用来逆转一个噪声过程。在离散世界 (如文本) 中，“噪声”通常意味着掩盖 (masking) token。

前向过程: 我们从干净的数据 \(x_0\) 开始。我们逐渐通过用特殊的 [MASK] token (表示为 0) 替换原始 token 来破坏数据。在时间 \(t=0\) 时，我们要么拥有原始句子。在时间 \(t=1\) 时，我们拥有一个纯掩码序列。

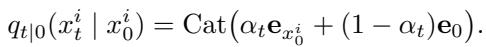
MDM 的前向过程方程。

在这里，\(\alpha_t\) 控制噪声调度。随着 \(t\) 从 0 到 1，一个 token 被掩盖的概率逐渐增加。

逆向过程: MDM 的目标是学习逆向操作: 给定一个部分被掩盖的序列 \(x_t\)，预测被掩盖 token 的原始值。

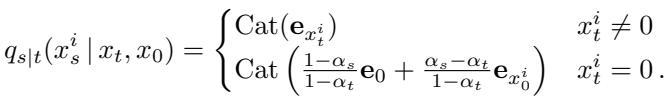
描述 token 如何被去掩码的逆向过程方程。

这里至关重要的区别在于组合数学 (combinatorics) 。 ARM 看到长度为 \(L\) 的序列并学习 \(L\) 次转换。然而，MDM 可能会看到被掩盖和未被掩盖 token 的任意组合。实际上，它必须学会如何在给定任意子集的情况下预测任何其他子集。

2. 为最坏的情况训练: 复杂性的负担

论文作者首先调查了一个紧迫的问题: 为什么 MDM 比 ARM 更难训练?

事实证明，MDM 的灵活性在训练期间是以高昂的代价换来的。因为 MDM 不知道在生成数据时会被要求使用哪种顺序，所以它必须学会处理所有顺序。

顺序无关 vs. 顺序感知

论文使用 \(\pi\)-learners (排列学习器) 的概念将这种区别形式化。

  • ARM: 使用固定的恒等排列 (从左到右) 。它是顺序感知 (Order-Aware) 的。
  • MDM: 实际上是对所有可能的排列进行平均。它是顺序无关 (Order-Agnostic) 的。

研究人员证明，与顺序感知训练相比, 顺序无关训练对于许多数据分布来说在计算上是难以处理的 。

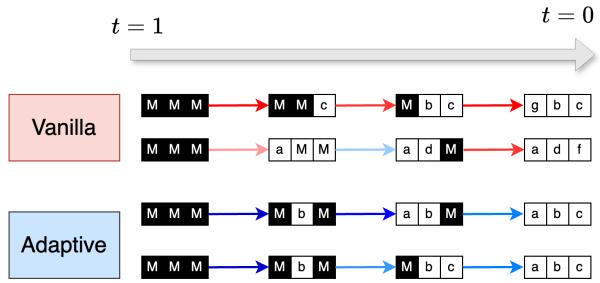
可视化 MDM 训练复杂性与推理灵活性。

如上图 1 的上半部分所示，训练一个 MDM 就像强迫一个学生学会随机地从中间、结尾或开头开始解决数学证明题。其中一些子问题是非常难的。

“潜变量与观测值”理论

为了从数学上证明这一点，作者引入了潜变量与观测值 (Latents-and-Observations, L&O) 分布模型。想象一个分两步生成的数据集:

  1. 潜变量 (隐藏种子) : 首先，生成随机的“种子”数字。
  2. 观测值 (结果) : 然后，根据这些种子使用一个函数 (例如哈希或逻辑规则) 计算可见的数字。

不对称性:

  • 如果你按照“自然”顺序 (种子 \(\rightarrow\) 观测值) 生成，任务很简单。你只需要运行函数即可。
  • 如果你按照“错误”顺序 (观测值 \(\rightarrow\) 种子) 生成，你必须反转函数。如果函数很复杂 (像哈希函数) ，这在计算上是不可能的。

ARM 如果按自然顺序训练，只会面临简单的任务。而 MDM 由于是在随机掩码上训练的，会频繁遇到“错误”顺序的子问题 (试图从观测值推测种子) 。

实证证据

作者不仅用数学，还用真实模型验证了这一理论。他们比较了以固定顺序 (ARM) 与随机顺序 (MDM) 学习文本的“难度” (似然度) 。

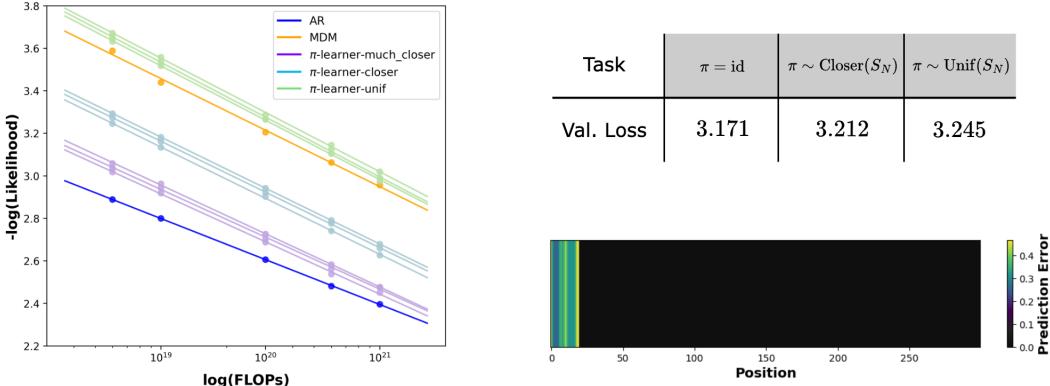
图表显示 MDM 似然度滞后和任务误差不平衡。

在图 2 (左) 中，我们可以看到这种复杂性的代价。在相同的计算预算 (FLOPs) 下，橙色线 (MDM) 的似然度 (负对数似然度较高) 始终比蓝色线 (ARM) 差。

图 2 (右) 的热力图则更具揭示性。它显示了“任务误差不平衡”。深色区域代表简单的任务 (观测值位置) ，而浅色区域代表困难的任务 (潜变量位置) 。MDM 在分布的“困难”部分挣扎得很厉害——而这些部分正是 ARM 凭借其固定顺序可以直接跳过的。

3. 做最好的规划: 自适应推理的力量

到目前为止，掩码扩散模型的前景看起来很黯淡。它们被迫学习难以处理的问题，并且在性能指标上受挫。那为什么还要费心研究它们呢？

这里蕴藏着论文的第二个、具有变革性的洞见: 你不必在推理时使用随机顺序。

虽然 MDM 在训练期间被迫学习困难的问题，但它同时也学会了简单的问题。在推理时，我们可以自由选择生成路径。我们可以“规划”我们的路线，避开难以处理的悬崖，坚持走在简单的山谷中。

摆脱随机性

标准 (朴素/Vanilla) MDM 推理模仿训练噪声过程: 它随机地去掩码 token。这是低效的，因为它冒着在模型准备好之前就要求其解决困难子问题 (如猜测种子) 的风险。

自适应推理 (Adaptive Inference) 改变了游戏规则。我们不再随机选择一组 token 进行去掩码，而是询问模型: “你对哪些 token 最有信心？”

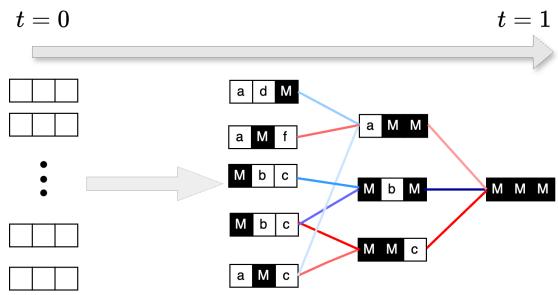
比较朴素推理路径和自适应推理路径。

如上图所示，朴素推理可能会选择一条需要尽早猜测困难 token 的路径 (例如 M \(\rightarrow\) b) 。而自适应推理则引导生成路径首先通过最简单的转换。

策略: 最高概率 vs. 边际

作者建议使用一个预言机 (Oracle) \(\mathcal{F}(\theta, x_t)\) 来选择接下来去掩码哪些 token。他们测试了两种主要策略:

  1. 最高概率 (Top Probability) : 去掩码模型赋予单个值最高概率的 token。

    \[ \mathcal{F} = \text{Top } K (\max_j p_\theta(x^i=j | x_t)) \]

    *问题: * 有时模型会“自信地犯错”，或者在两个非常可能的选项之间分配高概率 (例如，“猫坐在[垫子/帽子]上”) 。

  2. 最高概率边际 (Top Probability Margin，胜出者) : 去掩码最佳猜测与次佳猜测之间差距最大的 token。

    \[ \mathcal{F}(\theta, x_t) = \text{Top } K \left( |p_\theta(x^i = j_1 | x_t) - p_\theta(x^i = j_2 | x_t)| + \epsilon \right) \]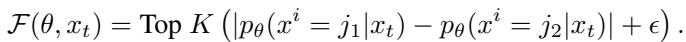

    最高概率边际的公式。

这种策略偏好模型没有歧义的 token。如果模型认为“垫子”和“帽子”的概率各占 50%，边际为 0，所以它会等待。如果它认为“垫子”是 99% 而“帽子”是 1%，边际很高，它就会去掩码它。

4. 实验结果: 碾压逻辑谜题

自适应推理的理论优势是巨大的，而在逻辑谜题上的实证结果更是令人震惊。

作者在数独 (Sudoku) 和斑马难题 (Zebra Puzzles/爱因斯坦谜题) 上测试了模型。这些是完美的测试平台，因为它们有一个“逻辑”解答顺序，而这个顺序很少是从左到右的。在数独中，无论格子在什么位置，你都会先解决可能性最少的那个格子。

数独对决

作者比较了三位竞争者:

  1. ARM (标准) : 从左到右训练。
  2. ARM (教师强制) : 明确地使用最优解答顺序进行训练 (这是巨大的优势) 。
  3. MDM (自适应) : 正常 (随机) 训练，但在推理时使用最高概率边际策略。

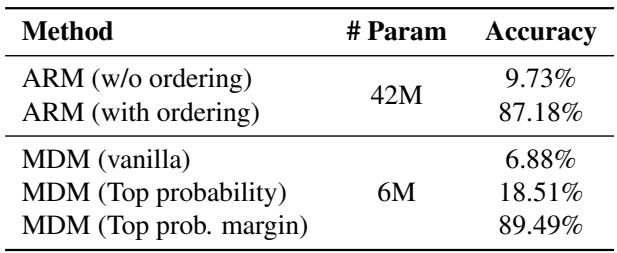
表格比较数独准确率。

注: 上表 (论文中的表 2) 显示了准确率的飞跃。

结果令人震惊:

  • 朴素 MDM: < 7% 准确率。 (随机猜测对逻辑题很糟糕) 。
  • ARM (标准) : ~10% 准确率。 (从左到右对数独来说很糟糕) 。
  • ARM (最优顺序) : 87.18% 准确率。 (知道顺序有帮助) 。
  • MDM (自适应边际) : 89.49% 准确率。

关键结论: MDM 从未被明确教过数独规则或正确的操作顺序，却即时自行找出了比经过正确顺序明确监督的 ARM 更好的解答顺序。

斑马难题

结果在需要复杂关系推理的斑马难题上也成立。

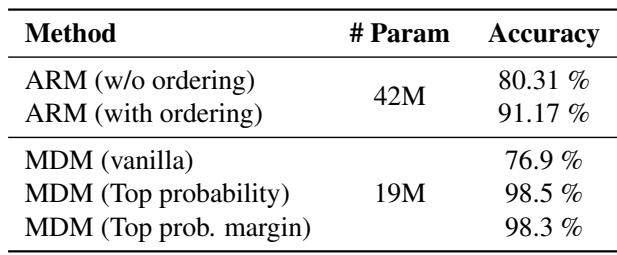
表格比较斑马难题准确率。

如表 3 所示，采用自适应推理的 MDM 达到了 98.3% 的准确率，超过了最佳 ARM 基线 (91.17%) 。

泛化到文本和数学

虽然逻辑谜题是亮点，但作者也展示了该技术适用于标准的大型语言模型。他们将自适应推理应用于 LLaDa 8B , 一个大型掩码扩散模型。

表格显示在 LLaDa 8B 上的表现。

在诸如 HumanEval (代码) 和 GSM8K (数学) 等困难推理任务上，自适应“最高概率边际”策略始终优于朴素推理。例如，在 HumanEval-Multi 上，性能从 16.5% (朴素) 跃升至 25.4% (边际) 。

我们在纯生成指标中也看到了这种好处。

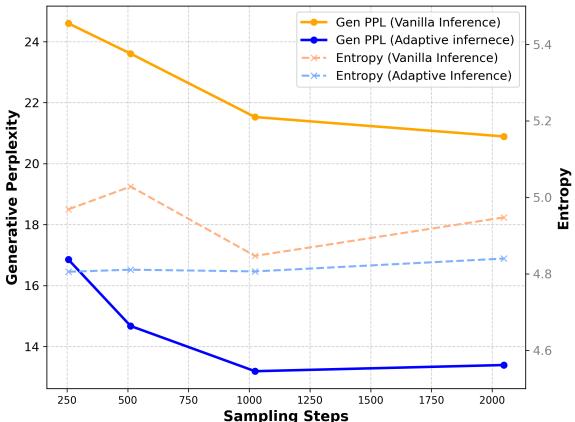
生成困惑度图表。

图 3 显示，与朴素推理 (橙色线) 相比，自适应推理 (蓝色线) 显著降低了困惑度 (衡量“惊奇”或错误的指标) ，在保持多样性的同时，有效地匹配了自回归模型的文本质量。

5. 结论: 未来是非顺序的

论文“Train for the Worst, Plan for the Best”为掩码扩散模型的“复杂性-灵活性悖论”提供了一个解决方案。

  1. 训练复杂性: 是的，MDM 面临比 ARM 更难的训练任务，因为它们必须学会从观测值预测变量 (“困难”方向) ，而不仅仅是按顺序生成变量。
  2. 推理灵活性: 然而，这种穷尽式的训练赋予了它们对数据的“整体”理解。它们知道序列所有部分之间的联系。
  3. 自适应能力: 通过使用像最高概率边际这样的策略，我们可以为每一个特定输入动态构建最佳生成路径。

最深刻的发现是 MDM 可以在没有监督的情况下发现最优推理路径 。 在数独中，模型自然地学会了先填最简单的数字，这种策略纯粹源于对其自身不确定性的统计特性。

这表明，对于需要规划、逻辑和非线性推理的任务，从左到右自回归模型的统治地位可能即将终结。通过为最坏的掩码情况进行训练，MDM 具备了独特的能力，可以为得出最佳解决方案进行规划。