解锁 AI 智能体的系统 2 思维: 蒙特卡洛树扩散

想象一下你在下一盘复杂的国际象棋。有时候，你会凭直觉瞬间走出一招——这是一种快速的模式匹配。而其他时候，你会靠在椅背上，推演未来几步的棋局，权衡各种选择，放弃糟糕的路径，并在触碰棋子前优化你的策略。

在认知科学中，这些通常被称为 系统 1 (快速、直觉性) 和 系统 2 (缓慢、深思熟虑) 思维。

在 AI 规划领域，扩散模型 (Diffusion Models) ——DALL-E 和 Midjourney 背后的技术——最近已成为出色的“系统 1”规划器。它们可以一次性生成复杂的轨迹。然而，它们在“系统 2”推理方面却很吃力。如果你给标准的扩散模型更多的时间去思考，它未必会变得更聪明；它只会生成另一个随机的猜测。

这篇博文将探讨一种名为 蒙特卡洛树扩散 (Monte Carlo Tree Diffusion, MCTD) 的新框架。该方法架起了扩散模型的生成能力与蒙特卡洛树搜索 (MCTS) 的战略深度之间的桥梁。通过阅读本文，你将了解我们如何最终让扩散规划器通过“思考”更长时间来产生更好的规划，从而解决难倒标准模型的复杂长视界任务。

问题: 当直觉不够用时

扩散模型通过将轨迹生成视为去噪问题，彻底改变了规划领域。扩散规划器不是一次预测一个动作 (这会导致误差累积) ，而是一次性生成整个路径。

轨迹通常表示为一个包含状态 \(s\) 和动作 \(a\) 的矩阵 \(\mathbf{x}\):

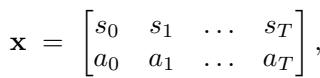
轨迹矩阵表示。

模型 \(p_{\theta}(\mathbf{x})\) 学习将这个矩阵从随机高斯噪声去噪为可行的规划。为了让智能体真正解决任务 (如到达目标) ，采样过程由一个估计轨迹价值或回报的函数 \(J_{\phi}(\mathbf{x})\) 进行引导:

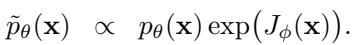
引导扩散采样的方程。

虽然这种方法有效，但它有一个上限。像 Diffuser 这样的标准扩散规划器提供的“推理时扩展性 (inference-time scalability) ”非常有限。如果模型未能在巨大的迷宫中找到路径，即使让它运行两倍的步数，通常收益也微乎其微。它缺乏一种结构化的方式来探索解空间、修剪糟糕的想法并优化好的想法。它缺乏推理能力。

解决方案: 蒙特卡洛树扩散 (MCTD)

为了解决这个问题，研究人员将目光投向了 蒙特卡洛树搜索 (MCTS) 。 MCTS 是 AlphaGo 成功的幕后推手。它通过模拟未来的结果来构建搜索树，使智能体能够将计算资源集中在有希望的路径上。

MCTD 结合了这两个世界。它将扩散去噪过程重新构想为一种树结构搜索。

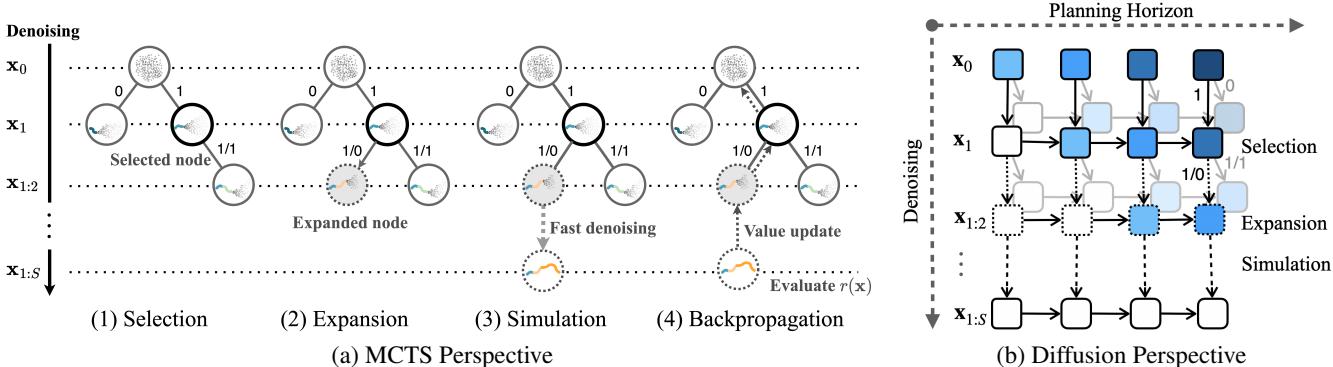
蒙特卡洛树扩散 (MCTD) 的两个视角。(a) MCTS 视角展示了树的生长。(b) 扩散视角展示了这如何映射到随时间和规划视界的去噪过程。

如上图 1 所示，MCTD 在两个轴上运行:

  1. 规划视界 (水平) : 在任务中随时间向前推进。
  2. 去噪深度 (垂直) : 将规划的质量从噪声优化为清晰。

通过融合这些概念，MCTD 实现了三项关键创新，使其能够随着算力的增加而扩展智能。

创新 1: 去噪即树的展开 (Tree-Rollout)

传统的 MCTS 逐个状态地构建树。如果一个规划需要 500 步，树就会变得极深 (\(Depth=500\)) ，难以处理。

MCTD 通过将轨迹 \(\mathbf{x}\) 分解为一系列 子规划 (sub-plans) (例如，每段 50 步) 来解决这个问题。搜索树中的节点不是单个状态，而是这些子规划。这使得树变得更浅且更易于管理。

规划器使用一种“半自回归”的方法。它生成第一个子规划，将其锁定，然后以第一个子规划为条件生成下一个子规划。在数学上，这将整个轨迹的概率近似为子规划的乘积:

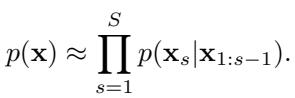
分解为子规划的概率。

这允许智能体逐块构建规划，但每一块都是由扩散模型生成的连贯片段。

创新 2: 引导等级作为“元动作 (Meta-Actions) ”

在标准的搜索树 (如国际象棋) 中，分支 (边) 代表离散的移动 (例如“兵走到 E4”) 。但在机器人技术中，动作空间是连续且无限的。你不可能对每一个可能的电机扭矩进行分支。

MCTD 引入了一个绝妙的抽象概念: 元动作 。

树的分支不再基于物理动作，而是基于 引导等级 (Guidance Levels) 。 在树的每一步，智能体决定 如何 使用扩散模型:

  • 无引导 (NO_GUIDE，探索) : 从先验中采样。这相当于问模型: “这里物理上合理的轨迹是什么？”，而不强迫它通过目标。这鼓励了多样性。
  • 引导 (GUIDE，利用) : 使用奖励函数进行采样。这相当于问: “给我找一条回报高的路径。”

通过动态地在这两种模式之间切换，搜索树平衡了探索新的可能性和优化有希望的路径。现在的条件概率包含了这个引导调度 \(\mathbf{g}\):

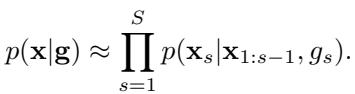
以引导元动作为条件的概率。

创新 3: 跳跃式去噪 (Jumpy Denoising) 作为快速模拟

在 MCTS 中，每当你添加一个新节点，你需要“模拟”到最后，看看它是否是一个好的位置。对于扩散模型来说，生成一个完整的规划既慢又昂贵。

MCTD 使用 跳跃式去噪 (基于 DDIM) 来进行模拟步骤。一旦创建了一个节点 (子规划) ，系统需要猜测轨迹的其余部分是什么样子的。它不进行高质量的慢速生成，而是运行一个“快进”版本，跳过许多去噪步骤:

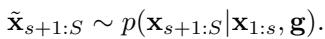
快速跳跃式去噪模拟的方程。

这提供了对规划最终质量的一个快速、粗略的估计 (\(\tilde{\mathbf{x}}\)) ，这足以指导搜索，而不会耗尽所有的计算预算。

MCTD 算法实战

MCTD 遵循经典的 MCTS 四步循环，并针对生成模型进行了调整。

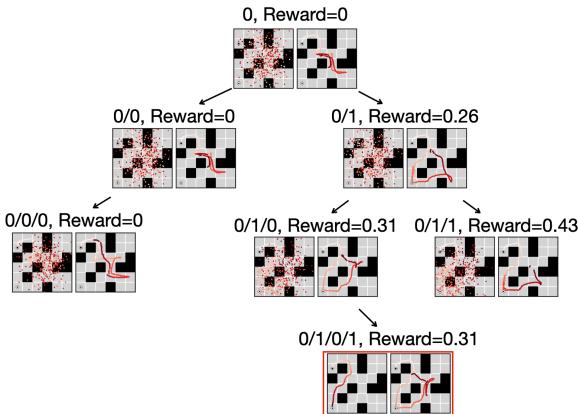
MCTD 树搜索过程的可视化。节点显示噪声规划变得清晰。分支代表引导选择。

  1. 选择 (Selection) : 算法遍历当前的树。它使用置信区间上界 (UCB) 来选择最有希望且尚未完全探索的节点。它在具有高价值的节点 (利用) 和访问较少的节点 (探索) 之间取得平衡。
  2. 扩展 (Expansion) : 一旦到达叶节点，算法就会扩展树。它使用扩散模型生成一个新的子规划。它选择一个“元动作” (引导或无引导) 来决定如何生成这个新片段。
  3. 模拟 (Simulation) : 为了评估这个新的部分规划，使用 跳跃式去噪 完成轨迹的其余部分。这是对剧集结束的一次快速、近似的展开。
  4. 反向传播 (Backpropagation) : 评估模拟出的完整规划的质量 (例如，“我们到达目标了吗？”) 。这个值会回传到树上，更新所有父节点的统计信息。

该算法通过生长这棵树来进行有效的“思考”。随着迭代次数的增加，它会找到更好的分支并放弃死胡同。

展示 MCTD 循环的算法 1 伪代码。

实验结果

添加这种“系统 2”结构真的有帮助吗？研究人员在具有挑战性的基准测试 (如 OGBench) 上测试了 MCTD，其中包括长视界迷宫导航和机器人操作。

1. 长视界迷宫

对规划最直接的测试就是复杂的迷宫。当视界很长时，标准扩散模型经常陷入局部最优或“臆想”出穿过墙壁的路径。

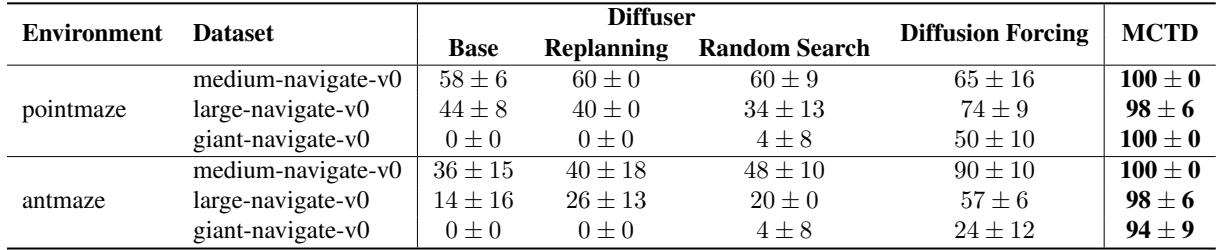
Pointmaze 和 Antmaze 上的成功率。MCTD 在巨型地图上始终达到近 100% 的成功率。

如表 1 所示, MCTD 在“巨型 (Giant) ”迷宫上实现了近乎完美的成功率 (94-100%) , 而标准的 Diffuser 甚至“Diffusion Forcing” (一个强大的基线) 都惨遭失败。

视觉对比阐明了原因:

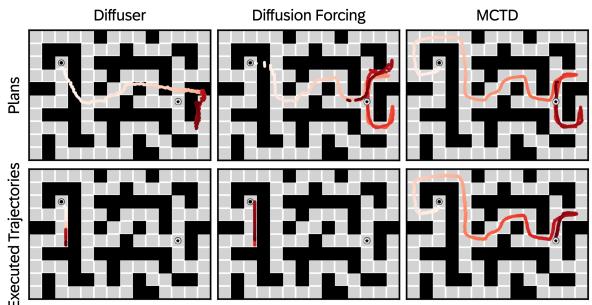
规划对比。Diffuser 和 Diffusion Forcing 未能找到有效路径。MCTD 成功导航了复杂的结构。

在图 2 中，你可以看到基线 (Diffuser) 产生了断开或无效的路径。MCTD 通过系统地搜索和修剪，找到了一条通往目标的连贯路径。

2. 机器人操作

研究人员还在操作多个立方体的机械臂任务上测试了 MCTD。这很难，因为它需要不同的阶段: 移动立方体 A，然后移动立方体 B。

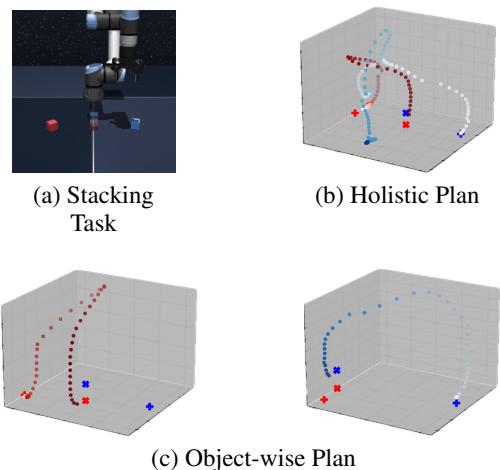
机械臂任务插图和轨迹可视化。

MCTD (特别是名为 MCTD-Replanning 的变体) 展示了处理多物体排序的强大能力。树搜索使其能够分离子目标 (移动不同的立方体) ，而不是试图将所有动作混合到一个纠缠不清的规划中。

机械臂操作的成功率。

3. 视觉规划 (部分可观测性)

当机器人只能看到像素时，这种方法还能奏效吗？团队创建了一个“视觉点迷宫 (Visual Pointmaze) ”，其中的输入是图像而不是坐标。这产生了 部分可观测性——机器人不知道它确切在哪里，只知道它看到了什么。

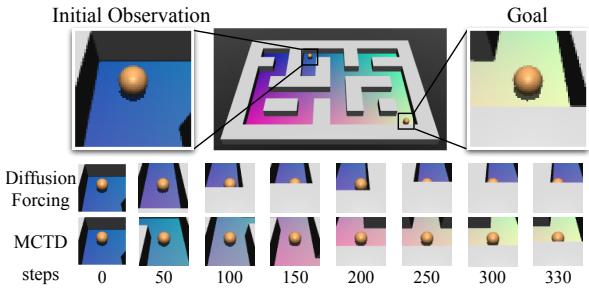
视觉点迷宫任务。上行: Diffusion Forcing 卡住了。下行: MCTD 找到了目标。

结果 (下表 3) 表明，MCTD 在这个更困难的设置中明显优于基线。树搜索有助于管理视觉观测中固有的不确定性。

视觉点迷宫结果表。

4. “思考更久”的力量

MCTD 的核心主张是 推理时扩展性 。 如果我们给模型更多的时间思考 (更多的去噪步骤/预算) ，它的表现会更好吗？

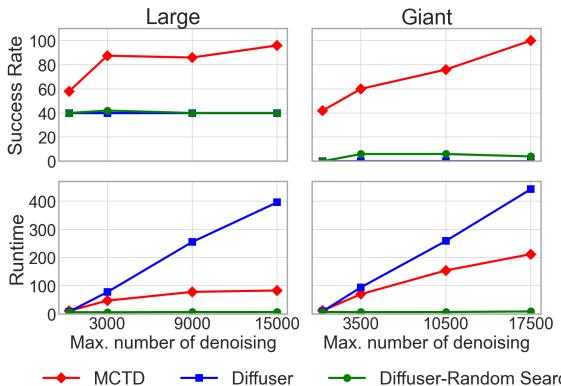
显示成功率和运行时间与去噪步骤预算关系的图表。MCTD 曲线及上升；其他保持平坦。

图 6 可能是最重要的结果。

  • Diffuser (橙色/绿色) : 即使增加计算预算，成功率也保持平坦。它触碰到了性能天花板。
  • MCTD (蓝色) : 随着预算增加，成功率稳步攀升，在巨型迷宫上接近 100%。

这证明了 MCTD 有效地将计算转化为智能，这是系统 2 推理的一个标志。

消融研究: 什么起作用？

研究人员进行了多项消融研究，以了解哪些组件驱动了成功。

  • 贪婪搜索 vs. 树搜索: 简单的贪婪搜索 (每一步从 \(K\) 个选项中选最好的) 在巨型地图上失败了 (0% 成功率) 。回溯和维护完整树的能力至关重要 (表 4) 。 显示贪婪搜索在巨型地图上成功率为 0% 的结果。

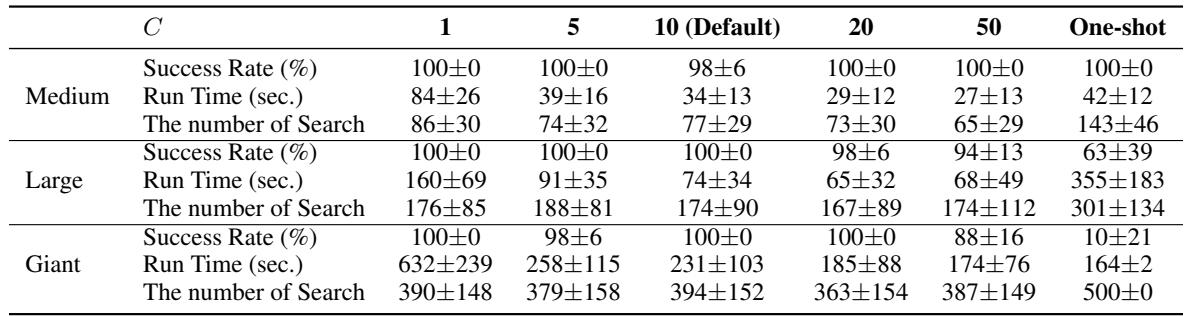
  • 跳跃式去噪比例: 模拟应该有多“跳跃”？如果太快 (One-shot) ，准确性会下降 (巨型地图上 10% 成功率) 。如果太慢 (\(C=1\)) ，运行时间会激增。平衡的比例 (\(C=10\)) 提供了最佳的权衡。 跳跃式去噪消融研究展示了速度与准确性之间的权衡。

结论

蒙特卡洛树扩散代表了 AI 规划向前迈出的重要一步。通过将 MCTS 结构化的、深思熟虑的搜索与扩散模型的生成能力相结合，它解决了“推理时扩展性”问题。

MCTD 允许智能体:

  1. 通过将规划分解为可管理的子树来 对长视界进行推理 。
  2. 使用引导等级作为元动作来 平衡探索与利用 。
  3. 利用跳跃式去噪进行快速模拟，从而 高效地思考 。

这个框架让我们离通用智能体更近了一步，这些智能体不仅能对环境做出反应，还能真正地规划、推理并适应以解决复杂问题。未来的工作包括让搜索更快，并自动学习元动作，为能力更强的系统 2 智能体铺平道路。