引言

如果你曾经训练过深度学习模型，那你很可能使用过 Adam 或 AdamW。这些自适应优化器是现代 AI 的引擎，驱动着从简单的分类器到大规模大语言模型 (LLM) 的一切。它们的工作原理是“运行时 (on-the-fly) ”适应损失函数的几何形状，根据训练过程中遇到的梯度来调整步长。

但这里有一个引人深思的问题: 为什么我们要把神经网络视为黑盒优化问题?

我们知道 Transformer 或 ResNet 的结构。是我们设计了它们。与其强迫优化器盲目地发现问题的几何结构，如果我们*先验地 (a priori) *将几何结构直接融入优化过程，会怎么样呢？

这就是这篇引人入胜的论文 《Training Deep Learning Models with Norm-Constrained LMOs》 (基于范数约束 LMO 训练深度学习模型) 的前提。研究人员提出了一族算法，不再局限于标准的梯度下降，而是转向基于线性最小化预言机 (Linear Minimization Oracles, LMOs) 的方法。

其结果就是 SCION , 一个具备以下特点的优化器:

  1. 通常优于 Adam 和 Muon。
  2. 允许超参数 (如学习率) 从微小模型完美迁移到巨大模型。
  3. 内存高效，只需存储一组权重和梯度。

在这篇文章中，我们将剖析这种方法背后的数学原理，解释为什么“范数约束”优化是一个颠覆性的改变，并看看其令人印象深刻的实证结果。

背景: 学习的几何学

要理解这篇论文的重要性，我们需要重新思考我们如何计算更新。

欧几里得 vs. 非欧几里得

标准的随机梯度下降 (SGD) 假设是欧几里得几何。它沿着负梯度的方向迈出一步。然而，神经网络的参数空间是复杂的。一个权重矩阵的微小变化可能会对输出产生巨大影响，而另一个矩阵的巨大变化可能毫无作用。

像 Adam 这样的自适应方法试图使用二阶矩估计来归一化这些更新。但还有另一种方法: 改变范数。

我们可以使用更能反映矩阵结构的范数，如谱范数 (Spectral Norm) 或无穷范数 (Infinity Norm) , 而不是使用标准的欧几里得距离 (L2 范数) 来衡量更新的“大小”。

线性最小化预言机 (LMO)

这篇论文中算法的核心原语是 LMO。

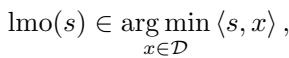
线性最小化预言机 (LMO) 的定义。

简单来说，如果你有一个约束集 \(\mathcal{D}\) (想象一个形状，比如球体或盒子) ，LMO 会接收一个方向向量 \(s\) (比如梯度) ，并找到该形状中与 \(s\) 的内积最小的点。

如果集合 \(\mathcal{D}\) 是一个由半径 \(\rho\) 定义的范数球:

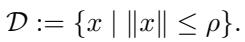
范数球约束集的定义。

那么 LMO 会找到该球体上指向最速下降方向最强烈的“角落”或边界点。

传统上，LMO 用于受限优化的条件梯度 (Frank-Wolfe) 方法——即你必须将参数保持在特定区域内。这篇论文做了一件聪明的事: 它将这一逻辑应用于无约束的深度学习问题。

方法: uSCG 和 SCION

作者介绍了两个主要的算法框架: uSCG (无约束随机条件梯度) 和 SCG (受限版本) 。

无约束 SCG (uSCG)

通常，Frank-Wolfe 算法使用凸组合 (加权平均) 来更新参数。uSCG 改变了这一点。它利用 LMO 来确定更新的方向和尺度，但像 SGD 一样将其直接添加到当前权重中。

这是 uSCG 的更新规则:

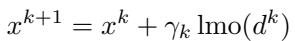
无约束 SCG (uSCG) 的更新规则。

这是使用动量计算“梯度” \(d^k\) 的方法:

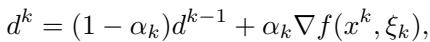
梯度方向的动量更新规则。

这种方法的强大之处在于 LMO 对更新进行了归一化 。 因为 LMO 总是返回范数球 \(\mathcal{D}\) 边界上的一个点，无论梯度是大是小，更新的幅度都由半径 \(\rho\) 固定。这使得算法对梯度消失或梯度爆炸具有极强的鲁棒性。

事实证明，许多现有的“奇异”优化器实际上只是选择了不同范数的 uSCG 的特定实例！

表格显示 uSCG 如何统一 Normalized SGD、SignSGD 和 Muon 等方法。

如表 1 所示，如果选择欧几里得球，你就复现了 Normalized SGD。如果选择最大范数 (无穷球) ，你就得到了 SignSGD。如果选择谱球，你会得到非常类似于最近的 Muon 优化器的东西。

SCION: 深度学习的算子范数

这篇论文最重要的贡献是 SCION (基于算子范数的随机条件梯度) 。

神经网络由将输入转换为输出的层组成。一层权重矩阵 \(W\) 的“大小”不应该仅仅是其平方项的总和 (Frobenius 范数) 。一个更好的衡量标准是该矩阵能将向量“拉伸”多少。这就是算子范数 (Operator Norm) 。

作者建议使用特定的算子范数来定义更新的几何形状。

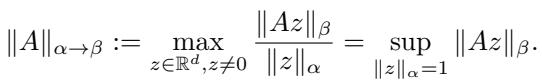
算子范数的定义。

通过选择输入范数 \(\alpha\) 和输出范数 \(\beta\)，我们可以推导出不同层的特定 LMO。

谱范数 (RMS \(\to\) RMS)

对于隐藏层，作者推荐使用谱范数 (具体来说，是从 RMS 范数到 RMS 范数的映射) 。谱范数的 LMO 涉及计算梯度的奇异值分解 (SVD) 。

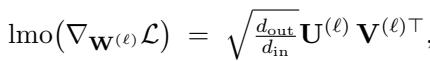
使用 SVD 的谱范数 LMO。

为什么要用谱范数？因为它控制了层的利普希茨常数 (Lipschitz constant) 。它确保无论层有多宽，流经网络的信号都不会爆炸或消失。这对于特征学习至关重要。

混合组合: ColNorm, Spectral, 和 Sign

不同的层有不同的作用。作者建议采用混合配置:

  1. 输入层: 使用 ColNorm (列归一化) 或谱范数。
  2. 隐藏层: 使用 谱范数 (Spectral Norm) 。
  3. 输出层: 使用 符号 (Sign) 更新 (无穷范数) 。

表 2 总结了这些选择及其相应的更新规则 (LMO) 。

不同算子范数及其关联 LMO 的表格。

“杀手级特性”: 零样本超参数迁移

深度学习中最令人头疼的问题之一就是调整学习率。你在一个小模型上调整好了，但当你扩展到一个更大的模型 (层更宽) 时，最佳学习率会发生偏移。你必须重新调整，这非常昂贵。

SCION 解决了这个问题。

因为更新是通过谱范数归一化的 (它内在也考虑了维度 \(d_{in}\) 和 \(d_{out}\)) ，最佳超参数可以在不同模型宽度之间完美迁移 。

这不仅仅是理论。看看在 NanoGPT 上的实验结果:

NanoGPT 上的超参数迁移结果。

在图 1 中，观察 “Scion” 和 “Unconstrained Scion” 的图表。从 64M 到 1B 参数的模型宽度曲线完美重合。最佳学习率 (曲线的最低点) 对于所有模型大小完全相同。

将其与 Adam (左上) 进行比较，在 Adam 中，随着模型变宽，最佳学习率会发生漂移。这意味着你可以在廉价的小模型上调整 SCION，然后立即使用相同的设置训练一个巨大的模型。

理论保证

虽然我们不会深入探讨证明细节，但这篇论文提供了严格的收敛性保证。

对于 uSCG , 非凸问题 (如深度学习) 的收敛速率推导如下:

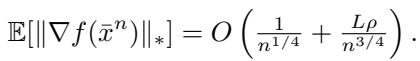
带有消失动量的 uSCG 收敛速率。

这个 \(O(n^{-1/4})\) 的速率与随机非凸优化的最佳收敛速率相匹配。

分析中的一个关键见解是 uSCG 不需要知道利普希茨常数 。 在标准的 SGD 中，如果步长相对于曲率 (利普希茨常数) 过大，就会发散。因为 uSCG 通过 LMO 对更新进行了归一化，所以步长具有鲁棒性。

实验与结果

作者在各种任务上对比了 SCION 与 AdamW 和 Muon (最近一种类似的基于谱的优化器) ，包括训练 GPT 模型和视觉 Transformer (ViT) 。

1. NanoGPT 性能

在训练 NanoGPT (一个标准的 Transformer 基准) 时，SCION 实现了比 AdamW 更低的验证集损失，并且匹敌或击败了 Muon。

至关重要的是，SCION 更节省内存。其实观只需要存储一组权重和一组梯度 (可以使用半精度) 。它消除了 Adam 中所需的二阶矩累加器，节省了大量的 GPU 显存。

2. 批量大小鲁棒性

随着训练规模的扩大，我们通常希望使用更大的批量大小以便在更多 GPU 上并行化。然而，许多优化器在批量较大时会变得不稳定或泛化能力变差。

SCION 对大批量大小表现出了卓越的鲁棒性。

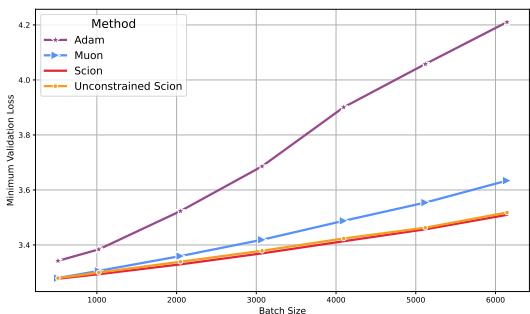
批量大小敏感性对比。

在图 2 中，你可以看到随着批量大小增加 (x 轴) ，Adam (紫色) 的验证集损失显著恶化。Muon (蓝色) 也有所恶化。然而，SCION (红色和橙色) 即使在非常大的批量下也能保持较低的损失。

3. ImageNet 训练

这种优势也延伸到了计算机视觉领域。在 ImageNet 上训练视觉 Transformer (ViT) 时，SCION 达到目标精度的 epoch 数比基线减少了 30% 。

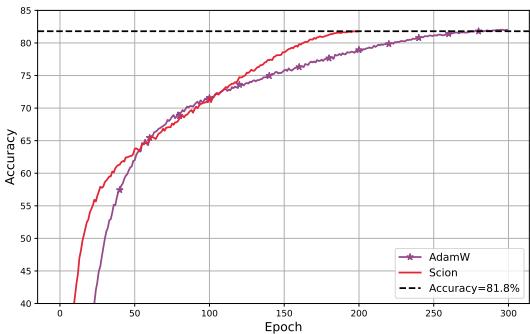
ImageNet 上 ViT 训练的结果。

由于 SCION 支持更大的临界批量大小，它还带来了 >40% 的实际运行加速 。

4. 扩展至 30 亿 (3B) 参数

为了证明该方法的可扩展性，他们训练了一个 30 亿参数的 GPT 模型。

3B 参数模型的验证集损失表。

如表 5 所示，与 Adam 和 Muon 相比，无约束 SCION 实现了最低的验证集损失。

实现: 实践中如何运作

实现 SCION 出奇地简单。对于谱范数层，我们需要计算 LMO，这需要梯度矩阵的最大奇异向量。计算完整的 SVD 太慢了，所以作者使用了 Newton-Schultz 迭代——一种在 GPU 上非常高效的 SVD 逼近迭代方法。

这是无约束 SCION 的通用算法:

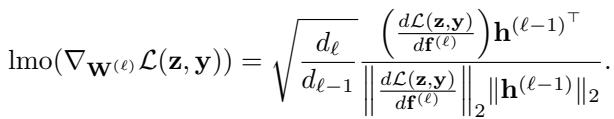
算法 3: 无约束 SCION。

注: 上图显示了 LMO 计算的细节，但算法循环很简单: 获取梯度 -> 更新动量 -> 计算 LMO (归一化) -> 更新权重。

我们还需要确保网络被正确初始化，以便在开始时范数是平衡的。作者建议使用特定的初始化策略 (如半正交初始化) 来匹配谱约束。

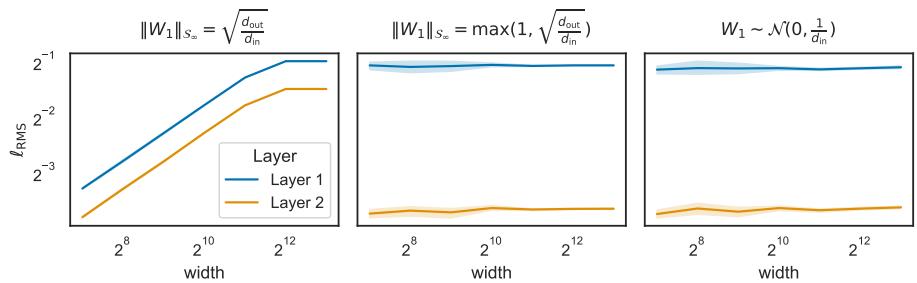
初始化时的坐标检查。

图 4 显示，使用正确的谱缩放 (中间和右侧图) ，无论宽度如何，激活值都保持稳定，而不正确的缩放 (左侧) 会导致信号爆炸或消失。

结论

论文《Training Deep Learning Models with Norm-Constrained LMOs》为替代占主导地位的 Adam 提供了一个令人信服的选择。通过退一步审视神经网络的几何结构，作者设计了 SCION , 这是一种具备以下特点的优化器:

  • 几何感知: 它使用适合深度网络架构的谱范数和算子范数。
  • 尺度不变: 它解决了超参数缩放问题，允许从模型到大模型的零样本迁移。
  • 高效: 它节省内存，并且对大批量大小具有鲁棒性。

随着我们继续训练越来越大的模型，自适应优化器的“黑盒”方法可能会达到其极限。像 SCION 这样先验地尊重模型结构的方法，代表了深度学习优化进化的下一个逻辑步骤。

如果你正在训练 Transformer 或大型 ConvNet，SCION 绝对值得一看——特别是如果你想节省超参数调整的时间，并从你的 GPU 中榨取更多性能。