引言

在当前的深度学习领域，我们正目睹着两种基本属性之间的一场激烈角逐: 并行化 (parallelization) 与表达能力 (expressivity) 。

一方面，我们拥有 Transformer 和像 Mamba 这样的状态空间模型 (SSMs) 。这些架构之所以占据主导地位，是因为它们在训练期间具有高度的可并行性。你可以输入一段文本序列，利用 GPU 同时处理所有 token。然而，这其中存在一个隐患。从理论上讲，这些模型属于一个特定的复杂性类别 (具体为 $TC^0$) ，无法完全解决内在的顺序问题，例如在有限状态机 (FSM) 中跟踪状态或解决复杂的奇偶校验问题。它们受限于“深度”。

另一方面，我们拥有经典的循环神经网络 (RNNs) 。RNN 顺序处理数据，逐步更新隐藏状态。这使得它们在状态跟踪问题上具有极强的表达能力——理论上它们可以模拟 FSM 能处理的任何算法。但是，它们的训练速度极其缓慢，因为你无法并行化这种顺序依赖关系 (第 $t$ 步必须等待第 $t-1$ 步完成) 。

这就引出了一个根本性的问题: 为了获得训练速度，我们必须牺牲进行顺序推理的能力吗?

一篇新的研究论文《Implicit Language Models are RNNs: Balancing Parallelization and Expressivity》 (隐式语言模型即 RNN: 平衡并行化与表达能力) 给出的答案是否定的。研究人员提出了隐式 SSM (Implicit SSMs) 。通过迭代一个变换直到其收敛到一个“不动点 (fixed point) ”，这些模型在训练时表现得像可并行的 Transformer，但在推理时却像无限深度的非线性 RNN。

如下图所示，结果令人震惊。当标准模型如 Mamba2 无法泛化到更长的序列或解决复杂的逻辑谜题 ($S_5$) 时，隐式 Mamba2 无论序列长度如何都能保持准确性。

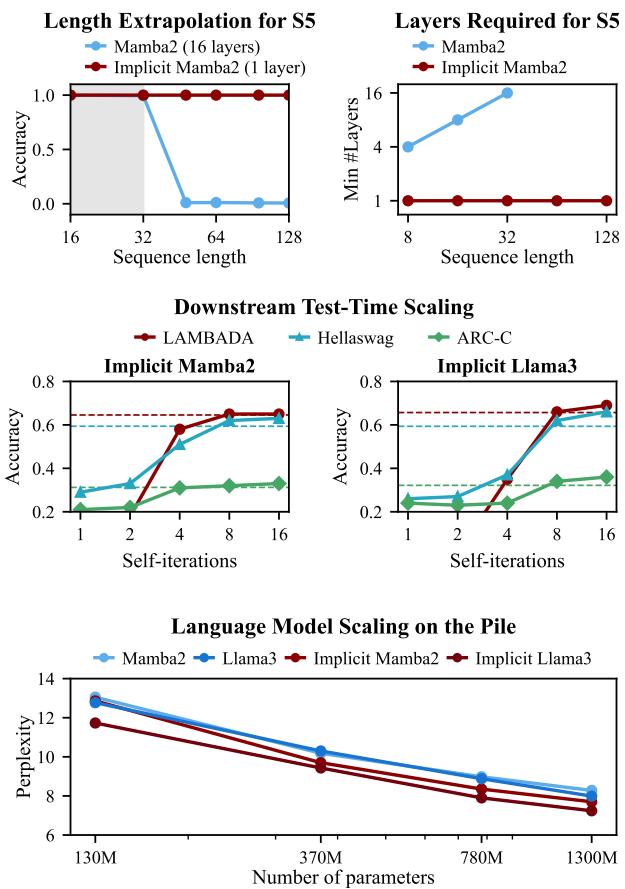
$左上: 解决 \$S _ { 5 }\$ 单词问题所需的最少层数。右上: 长度泛化比较。中间: 下游任务准确率。底部: 语言模型扩展。$

在这篇文章中，我们将剖析这篇论文，了解隐式模型的工作原理、其“无限”深度背后的数学原理，以及它们是如何扩展以训练拥有 13 亿参数的大型语言模型 (LLM) 的。

背景: 状态的错觉

要理解为什么隐式模型是必要的，首先需要了解当前架构的局限性。

显式模型的局限性

大多数现代语言模型都是“显式”的。这意味着它们由固定的层堆叠组成 (例如，Llama-2-7B 有 32 层) 。当一个 token 通过网络时，它会经历有限且预定次数的非线性变换。

最近的理论工作表明，这种有限的深度为计算能力设定了上限。具体来说，Transformer 和 SSM 在状态跟踪方面表现挣扎。想象一个问题，你需要跟踪一个物体在 100 次移动序列中在盒子 A、B 和 C 之间的位置。如果逻辑要求严格基于前一个状态来更新状态，标准的并行模型往往会失败，或者所需的层数随输入长度线性增加。

经典的 RNN 没有这个问题，因为它们的状态是顺序演变的。然而，正如前面提到的，我们要么不再使用它们，因为它们在现代硬件上无法扩展。

深度均衡模型 (DEQs)

研究人员从深度均衡模型 (DEQs) 中汲取了灵感。不同于标准网络 $y = f_3(f_2(f_1(x)))$，DEQ 隐式地定义其输出。它提出的问题是: “向量 $z^*$ 是什么，使得如果我再次将其通过网络运行，它不会发生变化？”

在数学上，我们寻找函数 $F_\theta$ 的不动点 $z^*$:

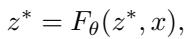
DEQ 的不动点方程。

找到这个 $z^*$ 通常涉及一遍又一遍地迭代函数 (自迭代) ，直到数值稳定。这意味着网络的“有效深度”会适应输入的难度。简单的输入收敛得快；困难的输入则需要更长时间。

核心方法: 隐式 SSM

研究人员提议将状态空间模型 (特别是 Mamba2) 的架构与 DEQ 的无限深度理念相结合。

架构

在标准的 SSM 中，隐藏状态 $h_t$ 使用线性递归进行更新: $h_t = \Lambda h_{t-1} + u_t$。这种线性特性使得 SSM 可以并行化 (使用并行扫描等算法) 。但这同时也是限制其表达能力的原因。

隐式 SSM 通过引入“深度”变量 $s$ 修改了这一点。我们在时间 $t$ 上处理序列，但在每个时间步，我们也在深度 $s$ 上“垂直”迭代直到收敛。

更新规则变成了不动点迭代:

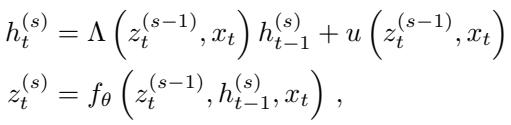
隐式 SSM 迭代方程。

这里:

$t$ 是时间步 (序列位置) 。
$s$ 是迭代步 (深度) 。
$h_t^{(s)}$ 是隐藏状态。
$z_t^{(s)}$ 是层输出 (或“思维”向量) 。

注意，转移矩阵 $\Lambda$ 和输入 $u$ 现在依赖于上一次迭代的输出 $z_t^{(s-1)}$。这将状态演变与深度迭代耦合在了一起。

两种运行模式: “二元性”

该论文最重要的贡献之一是定义了两种截然不同的计算这些不动点的方法。这种二元性使得模型能在不同场景下保持高效。

1. 同时模式 (Simultaneous Mode，最适合训练) 在这种模式下，我们一次性迭代整个序列。我们更新所有 token ($t=1$ 到 $T$) 的第 $s=1$ 次迭代，然后是所有 token 的 $s=2$，依此类推。因为底层的 SSM 核心是可并行化的，所以每次迭代 $s$ 都很快。这使得模型可以在 GPU 上高效训练。

2. 顺序模式 (Sequential Mode，最适合推理) 在这种模式下，我们完全解出 token $t=1$ 的不动点 (循环 $s$ 直到收敛) ，然后将最终状态传递给 $t=2$，解出 $t=2$，依此类推。这表现得完全像一个 RNN。

下图可视化了这种美妙的二元性。“同时”模式 (A) 允许轨迹在收敛期间相互作用，而“顺序”模式 (B) 则一次处理一个 token。

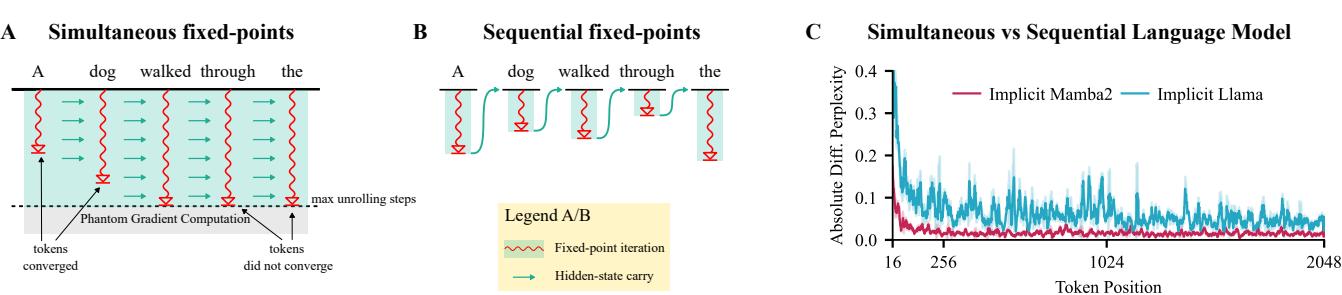
A: 迭代整个序列的同时模式。B: 逐个 token 迭代的顺序模式。C: 两种模式之间的困惑度差异。

面板 C 中的图表证实了两种模式产生的结果几乎相同 (困惑度差异极低) ，证明它们在功能上是等效的。

理论证明: 它就是 RNN

为什么要这么麻烦？研究人员提供了一个定理，证明在收敛时 (当 $s \to \infty$) ，SSM 的线性限制消失了。

在极限情况下，不动点变量 $h^*$ 和 $z^*$ 满足:

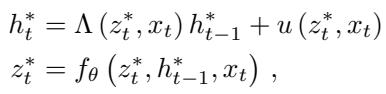
不动点极限方程。

研究人员推导了状态 $h_t^*$ 相对于前一个状态 $h_{t-1}^*$ 的雅可比矩阵 (变化率) 。在标准 SSM 中，这个雅可比矩阵是对角的且线性的。在隐式 SSM 中，雅可比矩阵变为:

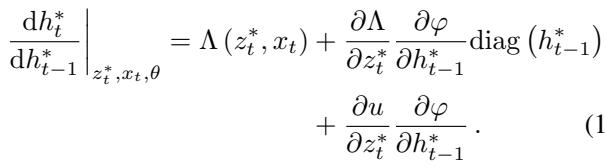
状态到状态的雅可比方程。

这个方程表明转移是非线性且非对角的。状态演变依赖于隐藏状态与输入之间复杂的相互作用。通俗地说: 隐式 SSM 在理论上已经将自己转变为一个非线性 RNN , 从而获得了解决令标准 Transformer 束手无策的复杂状态跟踪问题的计算能力。

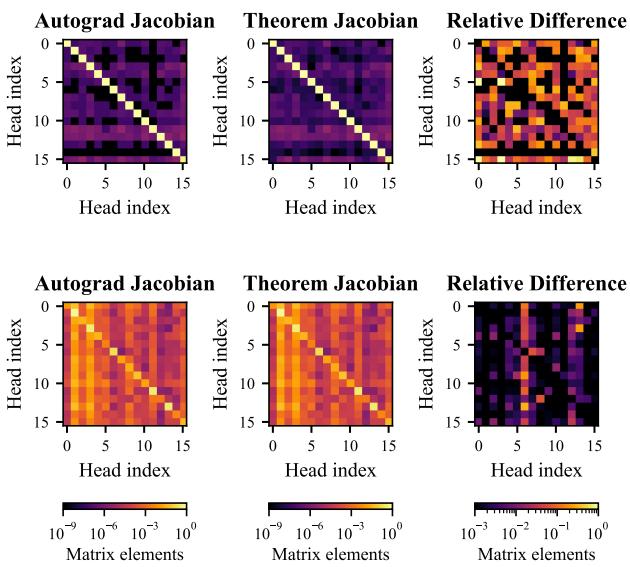
我们可以可视化这种非线性。下方的热图对比了通过自动微分 (Autograd) 得出的梯度与上述理论公式得出的梯度。非对角元素 (彩色图案) 的存在证实了模型正在学习复杂的状态依赖关系。

对比 Autograd 和定理公式的状态到状态雅可比热图。

使用幻影梯度 (Phantom Gradients) 训练

训练一个具有“无限”深度的模型听起来非常消耗内存。如果你展开一个循环 100 次，通常需要存储所有 100 步的激活值来执行反向传播。这会让最大的 GPU 内存也崩溃。

为了解决这个问题，作者利用了幻影梯度 (Phantom Gradients) 。这项技术依赖于隐函数定理。它指出，你不需要通过达到不动点的路径进行反向传播；你只需要计算最终不动点处的梯度。

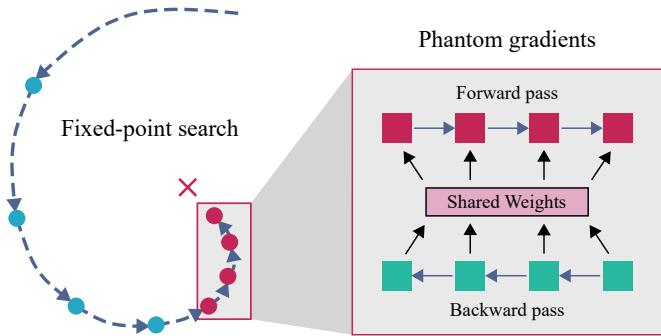
不动点迭代和幻影梯度示意图。

如上所示，前向传播迭代直到收敛 (左侧循环) ，但反向传播 (右侧) 只考虑解处的少量固定步骤 ($k$) 。这将内存使用与迭代次数解耦，允许模型在不消耗额外内存的情况下根据需要进行“思考”。

实验与结果

理论很完善，但实际效果如何？作者在合成逻辑谜题和大规模语言建模上测试了该模型。

1. $S_5$ 单词问题

这是一个专门设计用来难倒 Transformer 的基准测试。它涉及计算对称群 $S_5$ 的排列组合。这需要严格的、非交换的状态跟踪。

随着序列变长，标准 Mamba2 模型在完成此任务时会失败。它们仅仅是因为耗尽了用于跟踪状态变化的“层”。

然而，隐式 Mamba2 表现出色。下图 (左面板) 显示了在分布外 (OOD) 数据上的高准确率。中间面板特别有趣: 它表明你只需要在训练期间对迭代次数设定一个很小的上限 (例如 8 次迭代) ，就能学会通用算法，从而在测试时泛化到更难的问题。

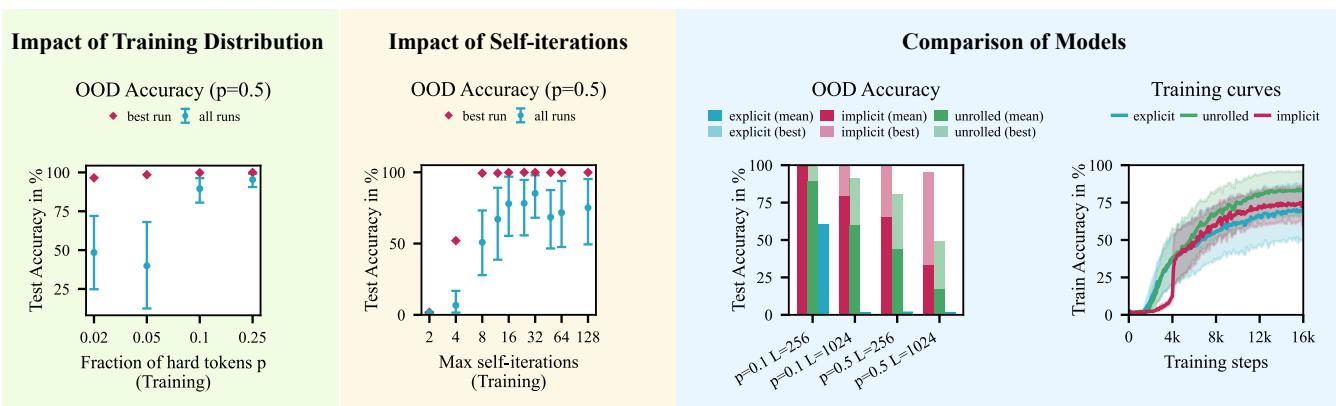
隐式与显式模型的 OOD 准确率和训练曲线比较。

右面板将隐式方法与“展开的” Mamba (即简单地堆叠层) 进行了比较。隐式 Mamba (红色) 比展开版本收敛得更快且更可靠。

2. 大规模语言建模 (13亿参数)

研究人员并未止步于玩具问题。他们在 Pile 数据集的 2070 亿个 token 上训练了高达 13 亿参数的隐式 Mamba2 和隐式 Llama 模型。这是迄今为止训练的最大的隐式模型。

长度外推 语言模型最理想的特性之一是能够在短序列上训练并在长序列上表现良好。标准模型在处理超过其训练窗口的序列时，通常会出现困惑度 (错误率) 爆炸。

下方的图 4 展示了长度外推能力。即使 token 位置远远超出了训练上下文 (灰色阴影区域) ，隐式模型 (红色和深红色) 仍能保持稳定、较低的困惑度。标准 Mamba2 (浅蓝色) 则显著退化。

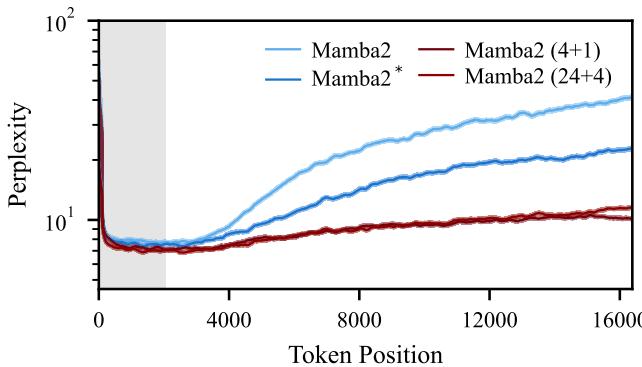
每 token 困惑度的长度外推性能。

下游推理 在常识推理任务 (如 LAMBADA、HellaSwag 和 ARC) 上，隐式模型通常优于其显式基线模型。

有趣的是，作者还使用了 CatbAbI 数据集——一个关于长故事推理的基准测试 (例如，“Fred 去厨房之前在哪里？”) 。

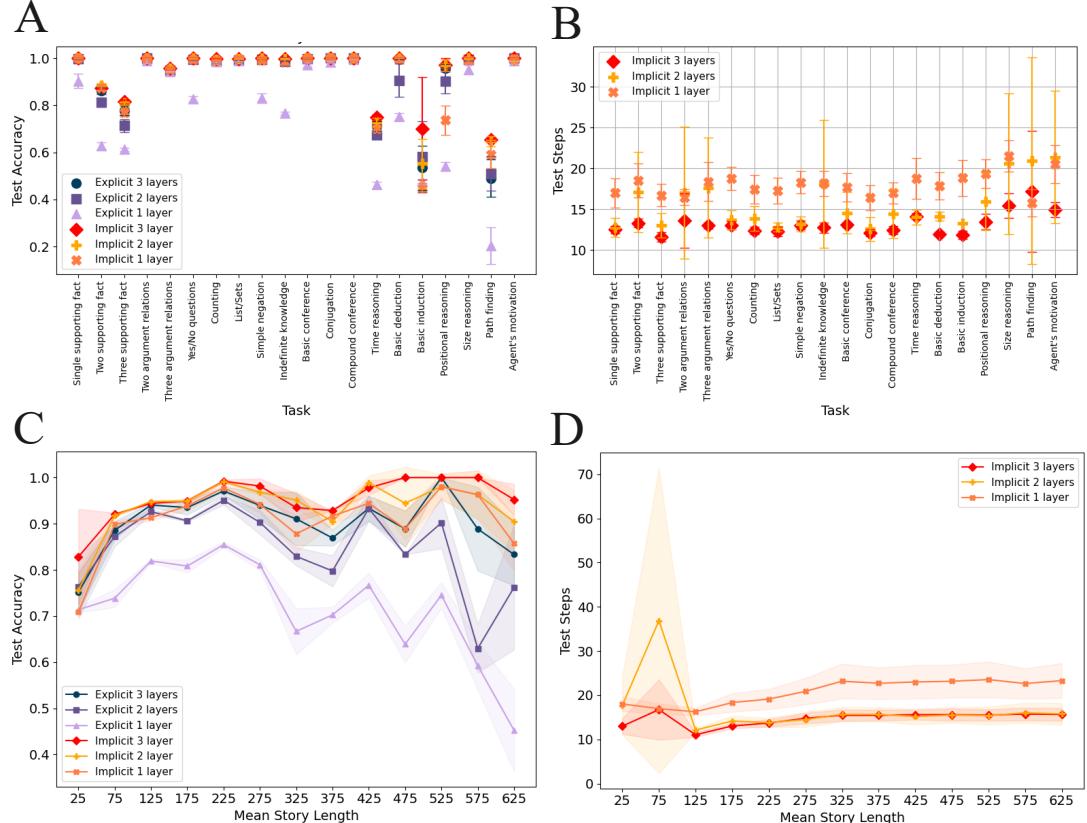
隐式 SSM 在 CATBABI 上的小规模推理优势。

图 13 中的面板 (c) 显示，随着故事长度的增加，隐式 Mamba2 (红色) 的准确率保持完美，而显式 Mamba2 (蓝色) 则崩溃了。面板 (d) 揭示了代价: 隐式模型会自动增加其迭代次数 (“Test Steps”) 来应对增加的难度。这就是实际运行中的自适应计算 (Adaptive Compute) ——当问题变难时，模型会思考更久。

结论与启示

论文《Implicit Language Models are RNNs》弥合了深度学习中的一个重大分歧。多年来，我们要么选择 Transformer/SSM 的训练效率，要么选择 RNN 的状态跟踪能力。这项工作表明，通过将模型层构建为不动点迭代，我们可以两者兼得。

关键要点:

隐式 SSM 就是 RNN: 通过自迭代，线性 SSM 获得了 RNN 的非线性状态转换能力。
二元性: 你可以在“同时模式” (并行/快速) 下训练，并在“顺序模式” (低内存/类 RNN) 下进行推理。
自适应计算: 模型自然地对更难或更长的序列使用更多的计算迭代，解决了困扰 Transformer 的长度泛化问题。
可扩展性: 这不仅仅是理论；借助幻影梯度确保内存效率，它在 13 亿参数规模上依然有效。

这种方法预示着未来的大型语言模型将不仅仅是静态的预测器，而是动态系统，能够对困难的提示进行“沉思”直到收敛出一个连贯的答案，同时保留大规模预训练所需的效率。

两全其美：隐式模型如何弥合 Transformer 与 RNN 之间的鸿沟

引言