在机器学习和统计学的世界里，我们经常渴望两件相互矛盾的事情: 一致性和隐私。

一方面，我们需要可复现性 (Reproducibility) 。 如果我今天在某个数据集上运行分析，而你明天在同一数据集上运行相同的分析，我们应该得到相同的结果。这是科学方法的基石。

另一方面，我们越来越需要差分隐私 (Differential Privacy, DP) 。 为了保护个体数据点，算法必须是随机的。如果一个算法是完全确定性的，它就有可能泄露其训练所用的具体输入信息。此外，像随机梯度下降 (SGD) 这样的标准训练方法本身就是设计成注入噪声以提高泛化能力的。

这就造成了一种张力。我们如何在算法的稳定性 (产生一致的输出) 与数学上必须的随机性之间取得平衡？

Max Hopkins 和 Shay Moran 最近发表的一篇论文《The Role of Randomness in Stability》 (随机性在稳定性中的作用) 探讨了这个基础性问题。他们不只是将随机性视为“噪声”，而是将其视为一种可以测量的计算资源——就像时间或内存一样。作者提出了一个深刻的问题: 为了实现算法稳定性，我们到底需要多少随机比特——也就是需要抛多少次硬币?

在这篇文章中，我们将深入探讨他们的发现。我们将探索确定性稳定性与随机可复现性之间的联系，这与差分隐私有何关系，以及这些概念最终如何解决不可知 PAC 学习 (Agnostic PAC Learning) 中的一个主要开放问题。

1. 稳定性动物园: 背景设定

在测量随机性之前，我们需要定义我们所说的“稳定性”是什么。这篇论文探索了一系列的稳定性概念，从弱的确定性保证到强的随机性保证。

全局稳定性: 确定性的天花板

想象一个算法 \(\mathcal{A}\)，它接收一个数据集 \(S\) 并生成一个模型。如果 \(\mathcal{A}\) 是确定性的，我们可能希望即使数据集 \(S\) 发生轻微变化 (例如，从相同的底层分布 \(D\) 中提取，但样本不同) ，它也能生成相同的模型。

我们将全局稳定性 (Global Stability) 定义为算法在两次独立的数据集抽取 \(S\) 和 \(S'\) 上输出完全相同结果的概率。

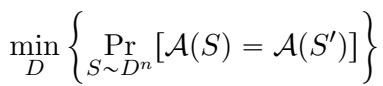
Formula for Global Stability optimization over distributions.

在这里，我们寻找的是在所有可能的数据分布 \(D\) 上的最小碰撞概率。

然而，这有一个陷阱。事实证明，对于任何非平凡的统计任务，确定性算法不可能做到完全的全局稳定。实际上，“全局稳定性”参数普遍被限制在 \(1/2\)。

为什么会有这个上限? 直观地说，想象一个分类问题，数据分布从“主要是 A 类”转变为“主要是 B 类”。在这个转变的某个点上，最优模型必须从预测 A 切换到预测 B。在这个确切的临界点上，确定性算法必须有效地“选边站”。如果它选择 A，它对 B 来说就是错的，反之亦然。这种不可避免的翻转造成了不稳定性。

这引出了“高频项 (Heavy Hitter) ”的定义。如果对于每个分布，都存在一个特定的输出 (一个“高频项”) ，其出现的概率至少为 \(\eta\)，我们就说该算法是 \(\eta\)-全局稳定的。

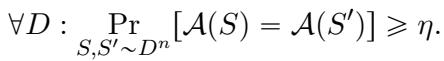
Formula showing heavy hitter global stability probability greater than eta.

可复现性: 引入共享随机性

既然确定性算法的稳定性上限是 \(1/2\)，我们如何实现近乎确定的可复现性这一科学理想呢？答案在于可复现性 (Replicability) 。

可复现性允许算法使用内部随机性，但有一个转折: 这种随机性在不同运行之间是共享的。可以把它想象成与算法一起发布的随机数生成器“种子”。

如果给定两个独立的数据集 \(S\) 和 \(S'\) 以及一个共享的随机字符串 \(r\)，算法的输出以高概率相同，那么该算法就是 \(\rho\)-可复现的:

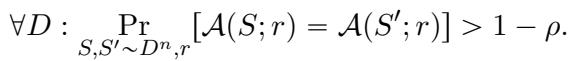
Formula for replicability with shared randomness r.

这是一个强得多的保证。它允许我们突破 \(1/2\) 的障碍。但这以此为代价: 我们需要生成并共享那个随机字符串 \(r\)。这引出了论文的核心度量指标: 证书复杂度 (Certificate Complexity) 。

证书复杂度 (\(C_{Rep}\)) 简单来说就是实现高可复现性 (具体来说，优于 \(1/2\)) 所需的最小随机比特数 (\(r\) 的长度) 。

差分隐私 (DP)

最后，我们有差分隐私。如果当我们改变输入 \(S\) 中的单个数据点时，算法的输出分布没有太大变化，那么该算法就是 \((\varepsilon, \delta)\)-DP 的。

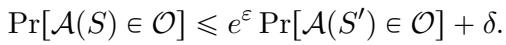
Standard definition of Differential Privacy inequality.

像可复现性一样，DP 本质上需要随机性。论文引入了DP 复杂度 (DP Complexity) , 用于计算在解决任务的同时满足此隐私定义所需的随机比特数。

2. 核心洞察: 从弱到强的提升定理

Hopkins 和 Moran 工作的核心在于“弱”概念的全局稳定性 (不需要随机性但概率低) 与“强”概念的可复现性 (具有高概率但需要随机性) 之间的一个惊人的等价性。

他们证明了一个 “从弱到强”提升定理 (“Weak-to-Strong” Boosting Theorem) 。 该定理指出，使算法可复现所需的随机比特数，实际上是由你在确定性条件下能达到的最佳稳定性决定的。

等价性

作者推导出了一个紧密的界限，将全局稳定性复杂度 (\(C_{Glob}\)) 和证书复杂度 (\(C_{Rep}\)) 联系起来。

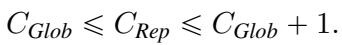
Inequality showing Global Complexity is roughly equal to Replicability Complexity.

这个等式意义深远。它表明全局稳定性和证书复杂度本质上是同一种资源。 如果你有一个确定性算法能以概率 \(\eta\) 命中正确答案，你可以使用大约 \(\log(1/\eta)\) 个随机比特将其提升为完全可复现。

提升是如何工作的 (阈值技巧)

你是如何神奇地将一个“弱”高频项 (例如出现概率为 10% 的输出) 转化为一个“强”可复现输出 (使用共享随机性出现概率为 99% 的输出) 的呢？

作者采用了一种涉及离散化舍入 (discretized rounding) 或随机阈值 (random thresholds) 的技术。

第一步: 估计概率 首先，在新鲜数据上多次运行弱全局算法，以估计每个可能输出假设的经验概率质量。比如说，假设 \(y_1\) 出现的概率是 12%，\(y_2\) 是 8%，依此类推。

第二步: 随机阈值 我们需要一致地选择一个假设。我们不能只选 max (最大值) ，因为如果两个假设的概率相近 (例如 12% 对 12.1%) ，微小的采样噪声会让 max 在它们之间反复横跳，从而破坏可复现性。

相反，我们使用共享随机性来选择一个随机阈值 \(t\)。

第三步: 选择 我们选择经验概率超过阈值 \(t\) 的第一个假设。

为什么这行得通? 这种方法唯一失效的情况是，某个假设的真实概率与随机阈值 \(t\) 非常接近。在这种情况下，采样噪声可能会导致经验估计值在不同运行中分别落在 \(t\) 的上方或下方。

但这里有个巧妙之处: 因为阈值 \(t\) 是随机选择的，所以它落在“危险区域” (紧挨着假设真实概率的区域) 的概率很低。

作者用一个“阈值过程”来说明这一点。

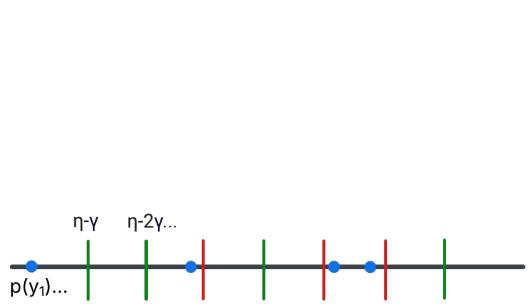
Diagram of the thresholding procedure with heavy hitters and thresholds.

在上图中:

  • 蓝点代表“高频项”假设的概率。
  • 垂直线代表可能的随机阈值 (由随机比特决定) 。
  • 绿线是“安全”阈值——它们离任何蓝点都足够远，噪声不会导致翻转。
  • 红线将是“不安全”阈值。

通过仅使用少量随机比特来选择一个绿色阈值，我们确保算法的两次运行 (在 \(S\) 和 \(S'\) 上) 将一致同意哪个假设越过了线。

这项技术证明了你可以“购买”稳定性。其代价正好是 \(\log(1/\eta)\) 比特，其中 \(\eta\) 是你的高频项出现的频率。

3. 将稳定性与隐私联系起来

在确立了可复现性和全局稳定性是同一枚硬币的两面之后，作者转向了差分隐私 (DP) 。

DP 通常更复杂，因为它取决于样本量 \(n\) 和置信度 \(\beta\)。作者定义了用户级 DP (User-Level DP) , 即我们要保护的是整个用户的数据集而不是单行数据。这简化了数学推导并加强了联系。

稳定性 \(\to\) DP

作者表明，如果你有一个全局稳定的算法，你可以用极少的额外随机性使其具有差分隐私。

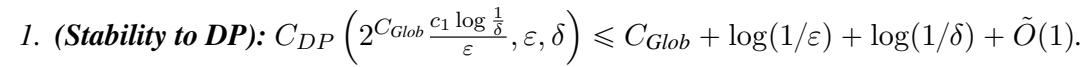
Inequality showing Stability implies DP with logarithmic overhead.

这个转换包含三个步骤:

  1. 高频项 (Heavy Hitters) : 使用全局稳定算法找到一系列可能的输出。
  2. DP 选择 (DP Selection) : 使用标准的隐私机制 (如指数机制) 从列表中选择一个假设。
  3. 有界支撑集 (Bounded Support) : 关键是，确保算法总是从一个小的、固定的集合 (支撑集) 中输出结果。

作者证明，任何具有小支撑集的分布都可以用极少的随机比特来近似。这使得他们能够构建一个在随机性方面极其高效的 DP 算法。

DP \(\to\) 稳定性

反过来成立吗？如果一个算法是差分隐私的，是否意味着它是全局稳定的？

是的。论文利用了一个叫做完美泛化 (Perfect Generalization) 的概念。事实证明，任何具有足够隐私性的算法也是“完美泛化”的，这意味着它在特定数据集上的输出分布与其在总体上的输出分布看起来非常相似。

如果输出分布是稳定的，它必须有“高频项” (频繁出现的输出) 。正如我们在第 2 节中学到的，如果你有高频项，你就拥有全局稳定性。

因此，这个闭环完成了:

  1. 全局稳定性 \(\approx\) 可复现性 (通过提升)
  2. 全局稳定性 \(\leftrightarrow\) 差分隐私 (通过高频项和 DP 选择)

4. 解决不可知 PAC 学习问题

上述理论机制不仅仅是为了展示。作者将其应用于学习理论中一个具体的开放问题: 不可知 PAC 学习 (Agnostic PAC Learning) 。

设定

  • PAC 学习: “概率近似正确 (Probably Approximately Correct) ”学习。我们要一种能以高概率输出低误差分类器的算法。
  • 不可知 (Agnostic) : 我们不假设数据完美契合我们的模型类 (例如，我们试图用直线拟合非完全线性的数据) 。我们只想要尽可能好的拟合。
  • 问题: 在不可知设定下，学习一个假设类 \(H\) 需要多少随机性？

先前的工作已经确定，在“可实现 (Realizable) ”设定 (存在完美模型) 下，随机性复杂度由 Littlestone 维度 (\(d\)) 控制。然而，尚不清楚这是否适用于更难的不可知设定。

结果

作者证明, 不可知 PAC 学习在随机性有界的情况下是可能的 , 当且仅当 Littlestone 维度是有限的。

具体来说，他们提供了一个学习器，其证书复杂度 (随机比特) 随维度 \(d\) 变化，并随误差 \(\alpha\) 呈对数增长。

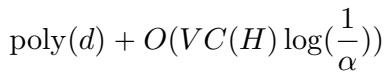
Complexity bound for certificate complexity in agnostic learning.

这里，\(VC(H)\) 是 VC 维度 (一种通常小于 Littlestone 维度的复杂度度量) 。\(O(\log(1/\alpha))\) 这一项是关键的胜利——它表明随着我们要求更高的精度，随机性成本增长得非常缓慢。

算法: 归约、提升、剪枝

他们是如何做到这一点的？他们将新的“稳定性提升”定理与一种归约技术结合起来。

  1. 可实现列表稳定学习器 (Realizable List-Stable Learner) : 他们从一个现有的针对较简单 (可实现) 情况的算法开始。该算法输出一个候选假设的列表。
  2. 不可知归约 (Agnostic Reduction) : 他们在许多未标记的样本上运行这个可实现学习器，以生成一个巨大的潜在假设池。
  3. 剪枝 (Pruning) : 这个池太大了。他们使用一个新的标记数据集来测试这些假设，并“剪掉”那些误差高的假设。
  4. 高频项 (Heavy Hitter) : 他们论证最优假设会频繁出现在这个剪枝后的列表中。
  5. 注入随机性 (Randomness Injection) : 最后，他们应用稳定性提升 (阈值) 技巧，使用共享随机性从这个列表中挑选出一个特定的假设。

这一逻辑链将一个混乱的、不可知的学习问题转化为一个干净、可复现的算法，并使用了精确数量的随机性。

5. 结论与启示

论文《The Role of Randomness in Stability》为算法稳定性提供了一个统一的视角。

对于学生和从业者来说，主要的收获是:

  1. 随机性是一种资源: 我们可以精确量化稳定性需要多少比特的随机性。它不是无限的；通常只是问题难度的对数级。
  2. 等价性: 确定性稳定性 (寻找高频项) 和随机可复现性 (对输出达成一致) 在计算上是等价的。你可以用少量的随机性将前者升级为后者。
  3. 隐私联系: 差分隐私与这些概念密切相关。如果你能私密地解决一个问题，你就能稳定地解决它，反之亦然。
  4. 学习理论: 该框架解决了不可知学习的随机性复杂度问题，证明即使数据充满噪声，高效、稳定的学习也是可能的。

这项工作有助于揭开机器学习中随机性这一“黑盒”的神秘面纱。它告诉我们，虽然我们无法消除隐私和稳定性对抛硬币的需求，但我们可以计算它们、优化它们，并确切地理解我们用每一个比特买到了什么。