收紧边界——利用新界限改进稀疏变分高斯过程

高斯过程 (Gaussian Processes, GPs) 是概率建模领域的“瑞士军刀”。它们提供了灵活性、非参数曲线拟合能力，以及最重要的——有原则的不确定性量化。然而，它们有一个众所周知的“阿喀琉斯之踵”: 可扩展性。标准 GP 的计算成本随着数据点数量的三次方 (\(O(N^3)\)) 增长，这使得它们在处理超过几千个数据点的数据集时变得不切实际。

十多年来，解决这个问题的标准方案一直是稀疏变分高斯过程 (Sparse Variational Gaussian Process, SVGP) 。 该方法由 Titsias 在 2009 年提出，通过使用“诱导点 (inducing points)”和变分推断，将复杂度降低到了 \(O(NM^2)\)，其中 \(M\) 是少量的诱导点。它已成为 GPflow 和 GPyTorch 等主流 GP 库中的默认设置。

但问题在于: 为了使数学计算易于处理，标准 SVGP 对诱导点和训练数据之间的关系做了一个基本假设。多年来，这一假设被认为是必要的。一篇新的研究论文 《稀疏变分高斯过程的新界限》(New Bounds for Sparse Variational Gaussian Processes) 对这一现状提出了挑战。作者证明，我们可以放宽这一假设，推导出一个严格更紧的证据下界 (ELBO)，并在不增加计算复杂度类别的情况下实现更好的预测性能。

在这篇文章中，我们将拆解 SVGP 的推导过程，找出近似可以改进的确切时刻，并逐步推导这个新的、更紧致的界限。

背景: 标准 SVGP 配方

为了理解这项创新，我们需要先建立基准。高斯过程在函数 \(f\) 上放置了一个分布。给定输入数据 \(\mathbf{X}\)，函数值 \(\mathbf{f}\) 服从由核函数 \(k\) 定义的多元正态分布:

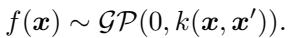
在回归设置中，我们观测到带有噪声的目标值 \(\mathbf{y}\)。我们的目标值和潜在函数值的联合概率为:

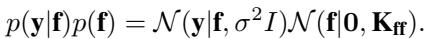
学习超参数 (如长度尺度和信号方差) 涉及最大化对数边际似然 \(\log p(\mathbf{y})\)。然而，计算它需要对协方差矩阵 \(\mathbf{K}_{ff} + \sigma^2 \mathbf{I}\) 求逆，这正是可怕的 \(O(N^3)\) 瓶颈的根源。

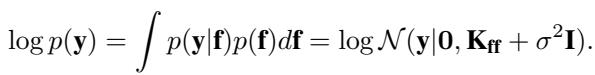
变分方法

为了扩展规模，SVGP 引入了诱导变量 \(\mathbf{u}\)。这些是在一组 \(M\) 个位置 \(\mathbf{Z}\) 上的函数值，这些位置与训练数据 \(\mathbf{X}\) 不同。其核心思想是，这 \(M\) 个点足以概括函数，从而预测剩余的 \(N\) 个点。

我们用这些诱导变量来增强模型。SVGP 框架的一个关键部分是如何定义数据 \(\mathbf{f}\) 和诱导变量 \(\mathbf{u}\) 的联合分布。我们将联合先验写为 \(p(\mathbf{f}, \mathbf{u}) = p(\mathbf{f}|\mathbf{u})p(\mathbf{u})\)，其中 \(p(\mathbf{f}|\mathbf{u})\) 是条件高斯分布。

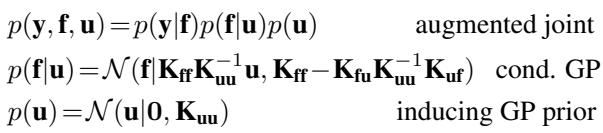
在变分推断中，我们用一个更简单的分布 \(q(\mathbf{f}, \mathbf{u})\) 来近似真实的后验 \(p(\mathbf{f}, \mathbf{u} | \mathbf{y})\)。然后，我们最小化 \(q\) 与真实后验之间的 Kullback-Leibler (KL) 散度，这等价于最大化证据下界 (ELBO)。

标准假设: 在原始的 SVGP 方法 (Titsias, 2009) 中，变分后验以一种非常特定的方式进行分解:

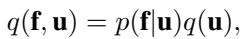
在这里，\(q(\mathbf{u})\) 是我们优化的自由变分分布 (通常是高斯分布) 。然而, \(p(\mathbf{f}|\mathbf{u})\) 是精确的条件先验 。

这个选择很方便，因为它使得在推导过程中各项可以很好地相互抵消，从而得到计算效率高的界限。由此产生的“塌缩 (collapsed)”界限 (其中 \(q(\mathbf{u})\) 已被求出最优解) 如下所示:

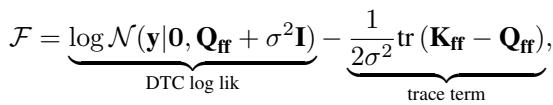
这个公式对于任何实施过 SVGP 的人来说应该都很熟悉。第一项是数据拟合项 (使用 Nyström 近似 \(\mathbf{Q}_{ff}\)) ，第二项是正则化迹项。

局限性

限制 \(q(\mathbf{f}, \mathbf{u}) = p(\mathbf{f}|\mathbf{u})q(\mathbf{u})\) 意味着给定诱导点 \(\mathbf{u}\)，训练点 \(\mathbf{f}\) 的行为完全遵循先验。来自观测数据 \(\mathbf{y}\) 的信息仅通过 \(\mathbf{u}\) 流入 \(\mathbf{f}\)。

但这真的是最优的吗？如果我们知道真实的后验 \(p(\mathbf{f}|\mathbf{u}, \mathbf{y})\)，它会像先验 \(p(\mathbf{f}|\mathbf{u})\) 吗？通常不会。真实的后验会结合来自 \(\mathbf{y}\) 的信息来调整 \(\mathbf{f}\) 和 \(\mathbf{u}\) 之间的相关性。通过强制我们的近似使用先验条件，我们限制了模型的表达能力，导致界限较松，并可能导致有偏的超参数学习 (通常表现为高估观测噪声) 。

核心方法: 放宽条件

研究人员提出了一种方法，通过用参数化分布 \(q(\mathbf{f}|\mathbf{u})\) 替换固定的先验 \(p(\mathbf{f}|\mathbf{u})\) 来收紧界限。

1. 分析精确后验

为了设计更好的近似，让我们看看精确条件后验 \(p(\mathbf{f}|\mathbf{u}, \mathbf{y})\) 实际上是什么样子的。如果我们能使用这个精确分布，KL 散度将消失，我们的近似将是完美的。

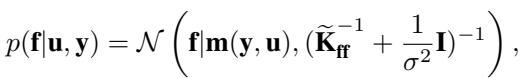
在这个方程中，\(\widetilde{\mathbf{K}}_{ff} = \mathbf{K}_{ff} - \mathbf{Q}_{ff}\)。均值 \(\mathbf{m}(\mathbf{y}, \mathbf{u})\) 很复杂，但协方差结构是关键。精度矩阵 (逆协方差) 是 \((\widetilde{\mathbf{K}}_{ff}^{-1} + \frac{1}{\sigma^2}\mathbf{I})\)。

我们可以使用矩阵恒等式重写这个精确后验的协方差:

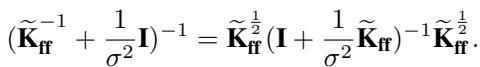
这个结构给了我们一个提示。由于数据项 \(\frac{1}{\sigma^2}\) 的存在，精确后验协方差比先验协方差“更小” (精度更高) 。标准 SVGP 实际上忽略了条件部分方差的这种减少。

2. 新的变分族

论文提出了一种新的 \(q(\mathbf{f}|\mathbf{u})\) 形式，它模仿精确后验的结构，但在计算上保持易处理。具体来说，他们引入了一个变分参数的对角矩阵 \(\mathbf{V} = \text{diag}(v_1, \dots, v_N)\)。

提出的分布是:

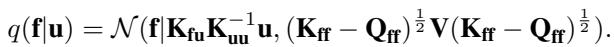
这一选择背后的逻辑如下:

1. 均值: 它保持与先验相同的均值 \(\mathbf{K}_{fu}\mathbf{K}_{uu}^{-1}\mathbf{u}\)。这使得期望值易于计算。
2. 协方差: 它用对角矩阵 \(\mathbf{V}\) 替换了精确后验中的逆项 \((\mathbf{I} + \dots)^{-1}\)。

这引入了 \(N\) 个新参数 (\(v_1\) 到 \(v_N\)) 。如果 \(V = I\) (单位矩阵) ，我们就恢复了标准 SVGP。如果优化 \(V\) 能让我们降低方差，我们就能得到更紧的界限。

3. 推导新界限

有了这个新的 \(q(\mathbf{f}|\mathbf{u})\)，ELBO 的推导就发生了变化。我们现在必须计算我们新的 \(q(\mathbf{f}|\mathbf{u})\) 和先验 \(p(\mathbf{f}|\mathbf{u})\) 之间的 KL 散度。

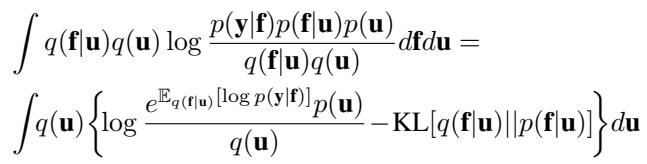
推导涉及两个主要部分:

1. KL 项: 由于两个分布都是高斯分布且均值相同，KL 散度显著简化。它仅取决于对角矩阵 \(\mathbf{V}\) 的迹和行列式。 \[ \text{KL} = \frac{1}{2}\sum_{i=1}^N (v_i - \log v_i - 1) \]
2. 期望对数似然: 这一项因新的协方差结构而改变。

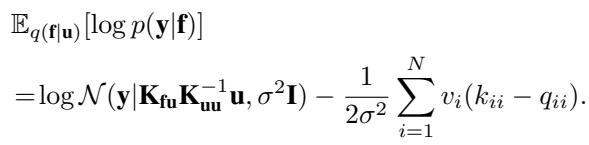
结合这些，我们得到一个依赖于 \(\mathbf{u}\)、超参数和我们新参数 \(v_i\) 的目标函数。

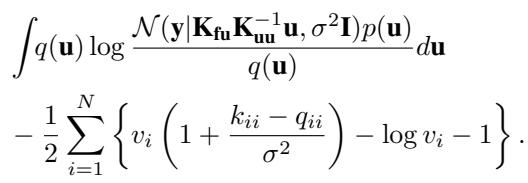
4. “塌缩”后的更紧界限

这里是最优雅的部分。我们实际上不需要使用梯度下降来寻找 \(v_i\)。上述界限相对于 \(v_i\) 是凹函数。我们可以求导，令其为零，并解析地找到最优的 \(v_i^*\):

当我们把这个最优 \(v_i^*\) 代回界限 (并且像标准 SVGP 那样解出最优的 \(q(\mathbf{u})\)) 时，我们得到了新的塌缩界限 :

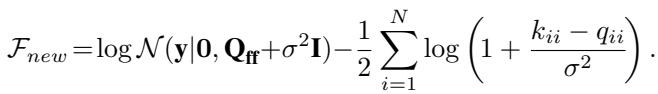
让我们将其与旧界限进行比较:

• 旧迹项: \(-\frac{1}{2\sigma^2} \sum (k_{ii} - q_{ii})\)
• 新对数项: \(-\frac{1}{2} \sum \log(1 + \frac{k_{ii} - q_{ii}}{\sigma^2})\)

利用不等式 \(\log(1+x) \le x\)，我们可以在数学上证明新项总是大于或等于旧项。由于我们是在最大化下界, 新界限严格更紧 (更好) ，只要诱导点没有完美地解释数据 (即当 \(k_{ii} - q_{ii} > 0\) 时) 。

本质上，新方法将近似误差的线性惩罚替换为对数惩罚，这更加宽容，且在数学上更接近真实的边际似然。

高效训练

SVGP 的优势之一是它能够使用随机梯度下降 (小批量) 进行训练，使其能够扩展到数百万个数据点。新方法会破坏这一点吗？

不会。未塌缩界限 (我们将 \(q(\mathbf{u})\) 保留为待优化的变分参数) 同样受益于 \(v_i\) 的解析解。

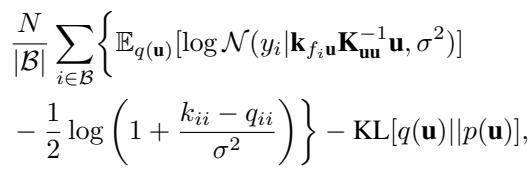
这个方程看起来很复杂，但在结构上与 GPflow 等软件中使用的标准随机 ELBO 完全相同，只是标量正则化项发生了变化。

• 复杂度: 复杂度仍然由诱导点的矩阵运算主导，\(O(M^3)\) 或 \(O(NM^2)\)，取决于具体实现。
• 存储: 我们不需要存储 \(N\) 个参数 \(v_i\)；它们是根据当前的核超参数和诱导点实时计算的。

扩展: 非高斯似然

如果我们进行分类或建模计数 (泊松回归) 怎么办？在这些情况下，似然 \(p(y|f)\) 不是高斯的，我们无法轻易地积分掉所有项。

标准方法使用求积法或蒙特卡洛采样来计算期望对数似然。新方法仍然适用，但为每个数据点优化一个独特的 \(v_i\) 变得昂贵，因为最优 \(v_i\) 不再有闭式解。

作者提出了一个折衷方案: 使用球形 \(\mathbf{V} = v\mathbf{I}\)。我们学习一个单一的标量 \(v\) 来调整所有数据点的方差。

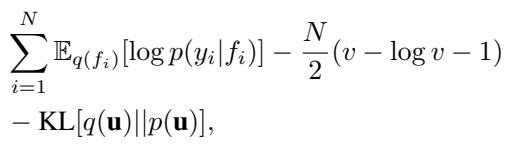
这仅向优化过程引入了一个额外的参数 (\(v\))，在保持效率的同时，仍然提供了比标准公式 (实际上强制 \(v=1\)) 更紧的界限。

实验与结果

论文在几个数据集上验证了新界限。

1. Snelson 1D 回归 (视觉证明)

Snelson 数据集是 GP 的经典“Hello World”。它有一个数据密度变化的复杂函数。

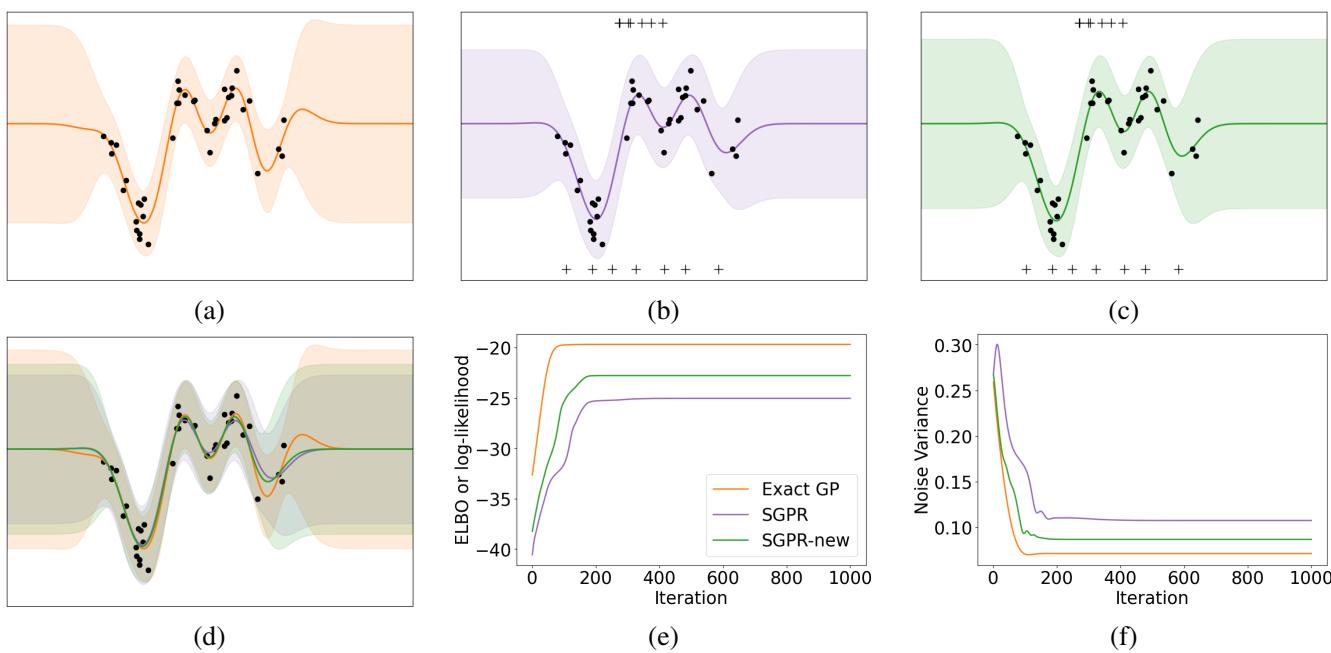
• 图 (a): 精确 GP (基本事实) 。
• 图 (b): 标准 SGPR (旧界限) 。注意预测方差有些膨胀。
• 图 (c): SGPR-new (提议的方法) 。方差更紧，并且与精确 GP 更加吻合。
• 图 (f): 此图显示了训练期间学习到的噪声方差 \(\sigma^2\)。标准 SGPR (紫色) 收敛到较高的噪声值，以补偿其较松的界限。新方法 (绿色) 收敛到较低的噪声值，几乎与精确 GP (橙色) 相同。

这证实了假设: 新界限减少了“欠拟合”偏差，即 SVGP 倾向于高估观测噪声。

2. 中等规模基准测试

作者比较了 UCI 回归数据集 (Pol, Bike, Elevators) 上的方法。

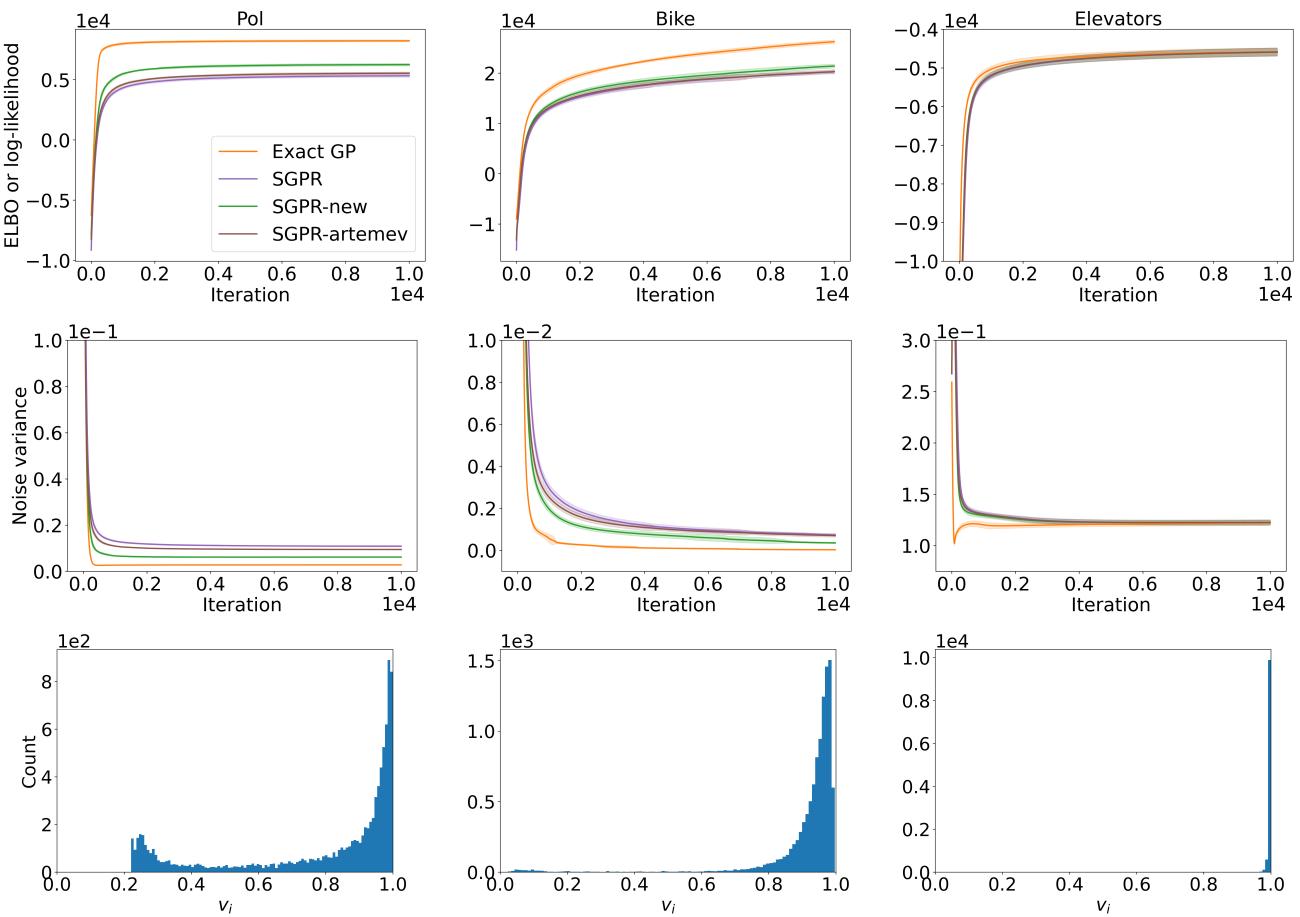
在图 2 中，我们看到了优化轨迹。

• 顶行 (ELBO): 绿线 (SGPR-new) 始终比标准方法获得更高的 ELBO。
• 底行 (直方图): 这显示了最优 \(v_i\) 值的分布。如果标准 SVGP 是最优的，所有 \(v_i\) 都应该是 1.0。事实上它们聚集在 0.8-0.9 左右，表明标准近似确实太松了，新参数正在积极修正协方差。

结果表加强了这一点:

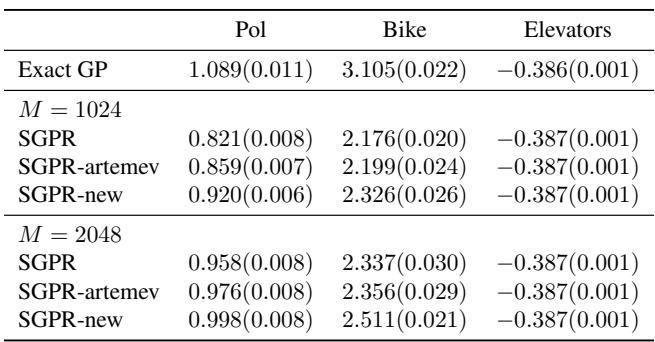
提议的方法 (SGPR-new) 实现了更高的测试对数似然，表明泛化能力更好。

3. 大规模与泊松回归

对于精确 GP 无法处理的大型数据集 (数百万个点) ，将新界限的随机版本与标准 SVGP 进行了比较。

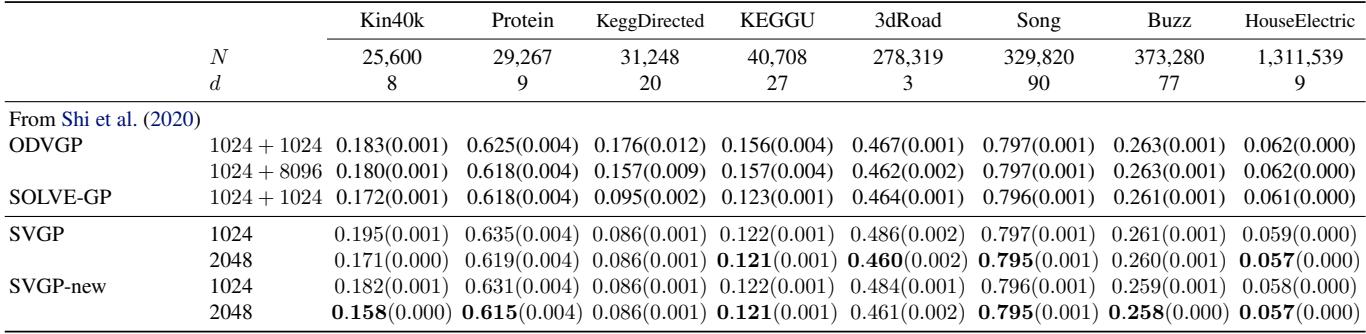
在像“HouseElectric” (130 万个点) 这样的数据集上，新方法始终略微领先于标准 SVGP 和其他基线。

最后，对于泊松回归 (计数数据) ，他们使用了标量 \(v\) 近似。

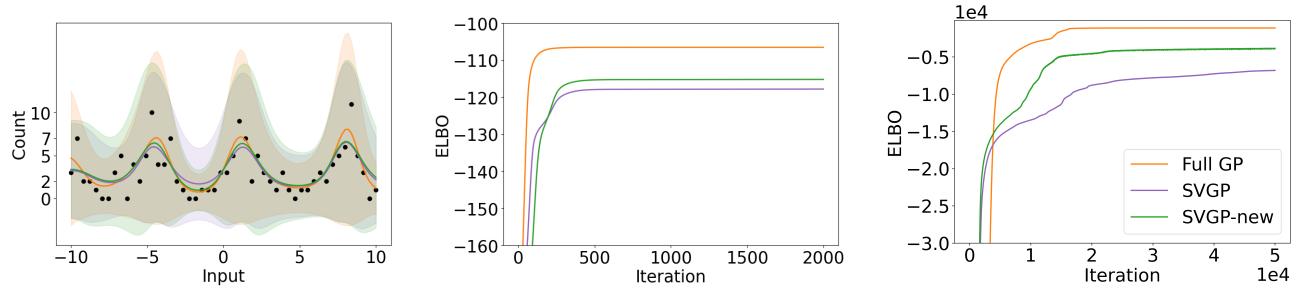
左图显示了计数数据的拟合情况。绿线 (New) 比紫线 (Standard SVGP) 更好地跟踪了橙线 (Full GP) 。ELBO 图 (中/右) 显示了明显的差距，证明即使是单个标量参数 \(v\) 也能显著提高非共轭似然的近似质量。

结论

这篇论文的贡献对高斯过程社区来说是一顿实实在在的“免费午餐”。通过放宽 \(q(\mathbf{f}|\mathbf{u}) = p(\mathbf{f}|\mathbf{u})\) 这一僵化的假设，作者推导出了一个新的界限，它:

1. 严格更紧: 数学上被证明是模型证据的更好下界。
2. 相同复杂度: 它符合相同的 \(O(NM^2)\) 计算类别。
3. 易于实现: 对于回归案例，它只需要更改损失函数中的一项 (迹项 \(\to\) 对数项) 。

对于学生和从业者来说，这一结果强调了质疑变分推断中“标准”假设的重要性。变分族的一个微小变化就可以在不需要更昂贵硬件的情况下，带来模型准确性和超参数学习的显著提升。随着 GP 软件库采用这些界限，我们可以预期稀疏 GP 将默认变得稍微更准确和鲁棒。