引言

在快速发展的生成式 AI 领域，我们经常被迫在速度、质量和训练稳定性之间做出选择。多年来，生成对抗网络 (GANs) 提供了快如闪电的单步生成能力，但饱受训练不稳定性 (即著名的“模式崩溃”) 的困扰。随后，扩散模型 (Diffusion Models) 的出现彻底改变了这一领域，带来了稳定的训练过程和惊人的图像质量，但代价巨大: 采样速度缓慢，需要数十甚至数百个迭代步骤来对单张图像进行去噪。

生成式建模的“圣杯”是将两个世界的精华结合起来: GAN 的单步生成速度，以及扩散模型的训练稳定性和生成质量。

来自麻省理工学院的研究人员提出了一种新颖的框架，或许正是我们寻找的答案。它被称为 混合分数训练 (Score-of-Mixture Training, SMT) 。 这种方法允许从头开始训练高质量的单步生成模型，既不需要对抗性训练的不稳定性，也不需要一致性模型 (Consistency Models) 中模拟概率流 ODE 的复杂性。

在这篇深度文章中，我们将探讨 SMT 的工作原理、其背后的数学直觉，以及它如何利用巧妙的“混合”概念来稳定学习过程。

生成模型的格局

为了理解 SMT 为何重要，我们首先需要看看它在当前生成模型格局中的位置。

1. GANs (生成对抗网络) : 训练一个生成器来欺骗判别器。它们最小化 Jensen–Shannon 散度 (JSD) 。虽然速度快 (单步) ，但对抗性的极小极大博弈很难稳定。
2. Diffusion Models (扩散模型) : 学习逆转噪声过程。它们使用去噪分数匹配 (Denoising Score Matching, DSM) 来学习“分数” (即数据分布的梯度) 。训练非常稳定，但生成过程缓慢。
3. Consistency Models (一致性模型) : 试图通过将轨迹上的点映射回原点，将缓慢的扩散过程“蒸馏”为单步。虽然前景广阔，但从头训练这类模型时，对噪声调度 (noise schedules) 的选择非常挑剔。

SMT 的作者提出了第四条路径。他们的目标是利用分数匹配直接最小化统计散度，从而消除了对判别器 (如 GANs) 或迭代积分 (如 Diffusion) 的需求。

如表 1 所示，SMT (及其蒸馏变体 SMD) 占据了一个独特的位置: 它提供稳定的单步生成，且无需预训练模型 (尽管如果有的话也可以利用) 。

核心直觉: 混合分数 (Score of Mixtures)

这就论文的核心创新在于将关注点从标准散度转移到一类称为 \(\alpha\)-偏态 Jensen–Shannon 散度 (\(\alpha\)-skew Jensen–Shannon Divergence, \(\alpha\)-JSD) 的散度上。

\(\alpha\)-JSD 的数学原理

标准的扩散蒸馏通常最小化反向 KL 散度。GANs 最小化标准 JSD。\(\alpha\)-JSD 是一个广义的家族，它在这些散度之间进行插值。

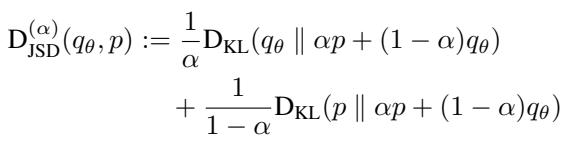
直觉如下:

• 当 \(\alpha \to 0\) 时，它的行为类似于 前向 KL 散度 (模式覆盖，mode-covering) 。
• 当 \(\alpha \to 1\) 时，它的行为类似于 反向 KL 散度 (模式寻找，mode-seeking) 。
• 当 \(\alpha = 0.5\) 时，它就是 GANs 中使用的标准 JSD。

通过在一定范围的 \(\alpha\) 值上最小化这种散度，模型既可以学习覆盖数据的多样性，又可以生成清晰、高质量的模式。

梯度与“分数”

为了训练神经网络生成器，我们需要计算该散度相对于生成器参数 (\(\theta\)) 的梯度。研究人员推导出了一个有趣的关系: \(\alpha\)-JSD 的梯度取决于 混合分布的分数 。

“分数”函数 \(\mathbf{s}(\mathbf{x})\) 简单来说就是对数概率密度相对于数据的梯度: \(\nabla_\mathbf{x} \log p(\mathbf{x})\)。它指向数据更有可能存在的方向。

生成器更新的梯度如下所示:

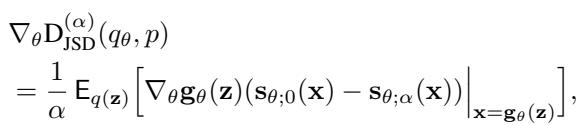
注意这一项 \((\mathbf{s}_{\theta;0}(\mathbf{x}) - \mathbf{s}_{\theta;\alpha}(\mathbf{x}))\)。

• \(\mathbf{s}_{\theta;0}(\mathbf{x})\) 本质上是生成 (伪造) 分布的分数。
• \(\mathbf{s}_{\theta;\alpha}(\mathbf{x})\) 是 混合分布 的分数: \(\alpha p(\mathbf{x}) + (1-\alpha)q_\theta(\mathbf{x})\)。

这告诉我们，要更新生成器，我们不需要一个判别器来说“是/否”。相反，我们需要一个能够估计真实数据和生成数据 混合 后分数的模型。

混合分数训练 (SMT) : 从头训练

SMT 框架通过在两个任务之间交替来创建一个稳定的训练循环:

1. 分数估计: 训练一个网络来估计真实分布和生成分布混合后的分数。
2. 生成器更新: 使用这些估计的分数将生成器的输出推向真实数据分布。

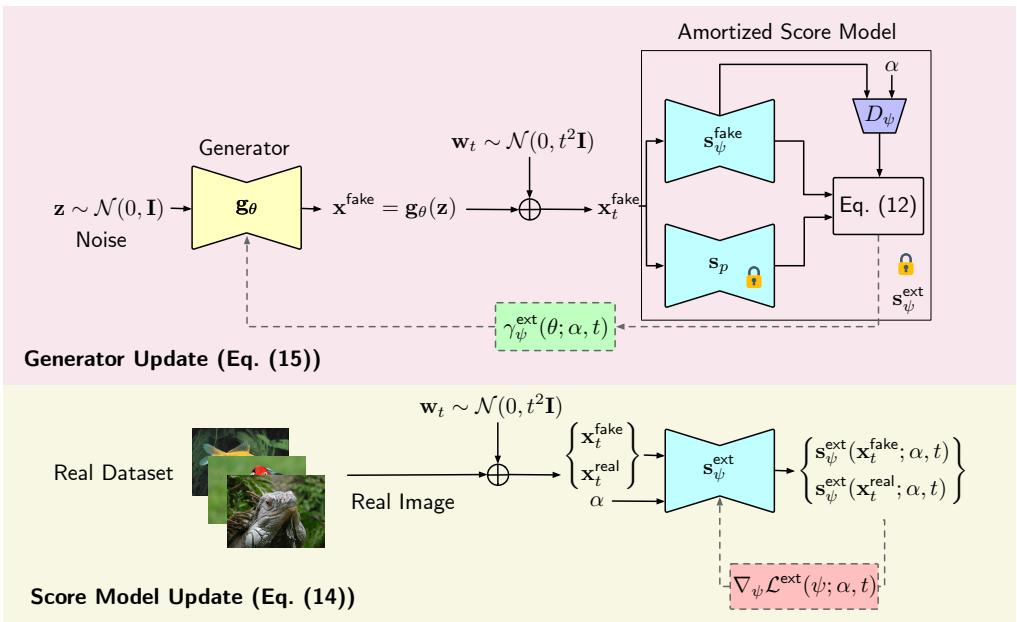
架构

为了高效实现这一点，作者引入了 摊销分数模型 (Amortized Score Model) 。 他们没有为每个可能的混合权重 \(\alpha\) 训练单独的模型，而是训练一个单一的神经网络 \(\mathbf{s}_\psi(\mathbf{x}; \alpha, t)\)，该网络将 \(\alpha\) 和噪声水平 \(t\) 作为输入。

这创建了一个高效的系统。分数模型学习了真实分布和生成分布在不同噪声水平下如何重叠的几何结构。

训练循环

让我们通过可视化来了解整个过程。

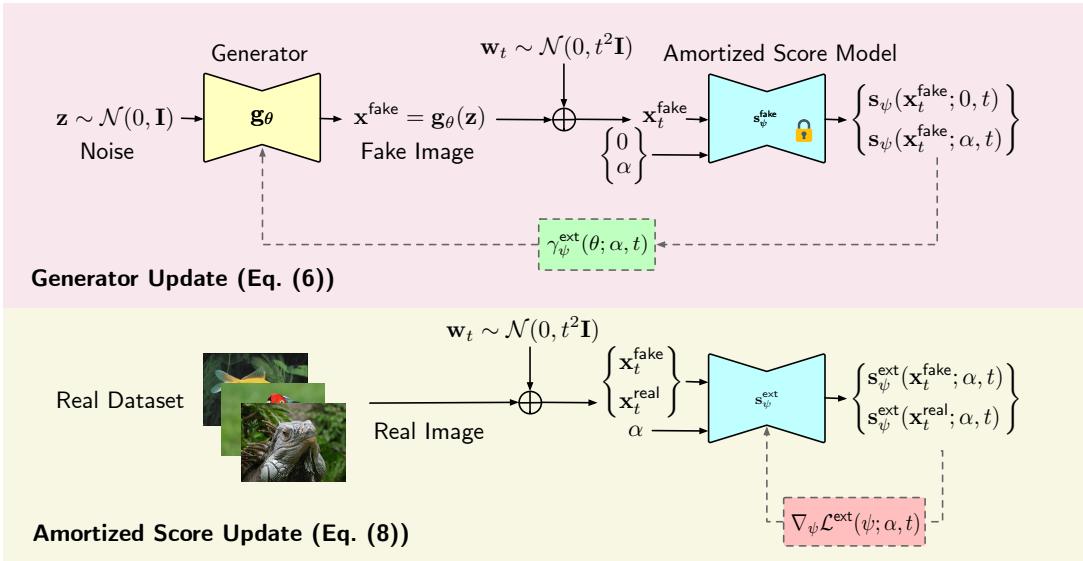
在底部路径 (分数更新) 中: 我们获取真实图像和生成图像 (由当前模型生成) 。我们通过要求分数模型学习混合分布的分数来隐式地混合它们。这是使用标准的去噪分数匹配 (DSM) 完成的，众所周知 DSM 非常稳定。损失函数如下所示:

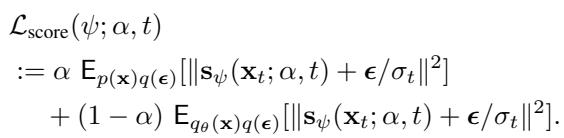
在顶部路径 (生成器更新) 中: 我们冻结分数模型。我们生成伪造图像，添加噪声，然后根据“纯”生成分数和“混合”分数之间的差异计算梯度。这个梯度会微调生成器的参数 \(\theta\)，使得生成的分布更接近真实分布。

生成器更新使用了从 \(\alpha\)-JSD 梯度推导出的近似值:

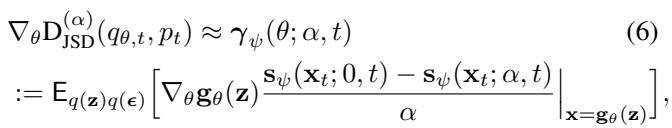
这种方法避免了 GANs 的“极小极大”不稳定性，因为分数模型始终试图最小化回归损失 (它预测噪声的能力如何) ，这比在零和博弈中试图击败生成器要容易得多。

自适应加权

显著提升性能的一个实现细节是梯度的加权方式。作者引入了一个特定的加权项 \(w(\mathbf{x}_t, \mathbf{x}, \alpha, t)\)，以确保训练信号在整个过程中保持强劲且稳定。

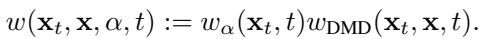
这种加权将标准的扩散权重与特定于混合几何结构的项结合起来，确保 \(\alpha \to 0\) 或 \(\alpha \to 1\) 的极端情况都不会对学习产生非生产性的主导影响。

混合分数蒸馏 (SMD)

如果你已经有一个强大的预训练扩散模型 (如 Stable Diffusion 或 ImageNet 模型) 怎么办？你不想从头学起，只想将那个缓慢的模型蒸馏成一个快速的单步生成器。

这就是 混合分数蒸馏 (SMD) 发挥作用的地方。

在 SMD 中，我们将预训练模型视为真实数据的“基准 (ground truth) ”分数 \(\mathbf{s}_p(\mathbf{x})\)。因为我们要真实数据的显式表示，所以不需要“盲目”地学习混合分数。我们可以显式地分解混合分数:

在这里，\(D_{\theta;\alpha}\) 的作用有点像判别器——它表示真实数据与生成数据之间的概率比。

在 SMD 框架中:

1. 我们学习一个 生成分数模型 \(\mathbf{s}_{\psi}^{\text{fake}}\) (当前生成器分布的分数) 。
2. 我们学习一个 判别器 \(D_\psi\) (密度比) 。
3. 我们利用预训练的教师模型 \(\mathbf{s}_p\) 将它们结合起来得到混合分数。

这种显式参数化允许非常高效的蒸馏。生成器利用预训练模型作为向导来最小化 \(\alpha\)-JSD，仅需其他方法的一小部分算力即可达到最先进的结果。

实验与结果

作者在两个标准基准上测试了 SMT 和 SMD: ImageNet 64x64 和 CIFAR-10 。 使用的指标是 FID (Fréchet Inception Distance) ，数值越低越好。

定量性能

结果非常令人印象深刻。如表 2 所示，SMT (从头训练) 在 ImageNet 64x64 上实现了 3.23 的 FID。这优于一致性训练 (CT) ，且与参数量翻倍的“iCT-deep”模型相当。

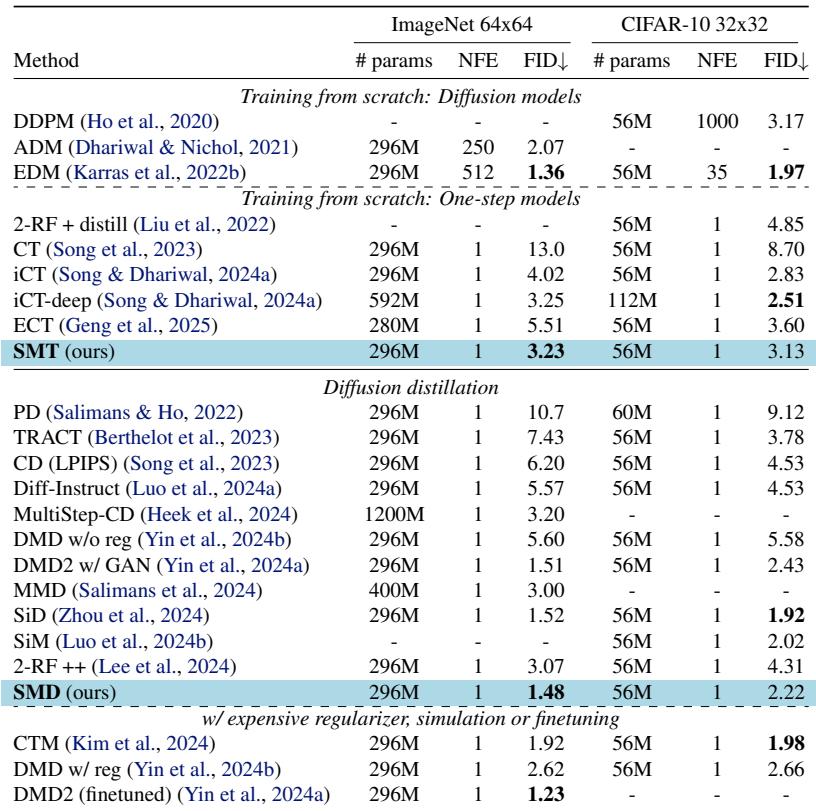
对于蒸馏 (SMD) ，结果甚至更强。SMD 在 ImageNet 64x64 上实现了 1.48 的 FID。这击败或媲美了复杂的方法，如一致性轨迹模型 (CTM) 和分布匹配蒸馏 (DMD2) ，同时实现起来更简单。

训练稳定性

论文的主要主张之一是稳定性。在 GANs 中，损失曲线经常剧烈震荡。在一致性模型中，调整噪声调度非常棘手。

作者可视化了 SMT 的训练动态。

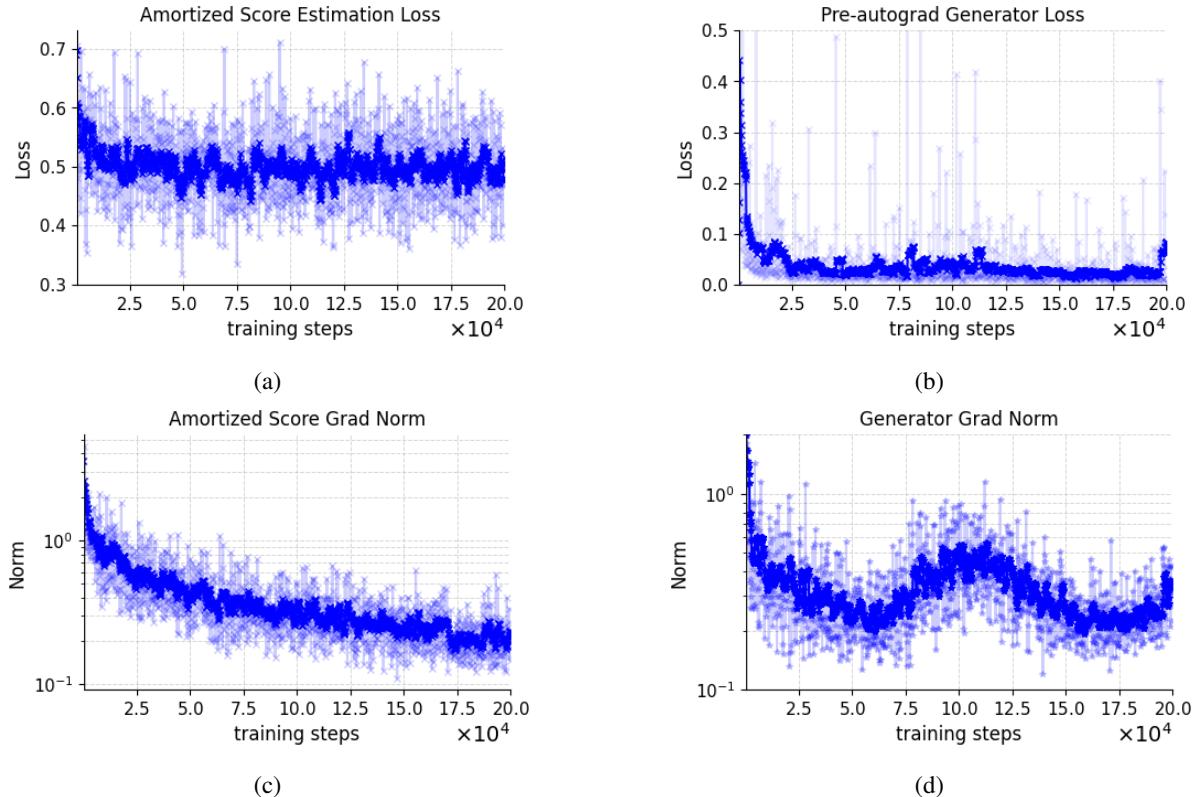
图 8 中的曲线显示了平滑、稳定的收敛。损失没有爆炸，梯度范数也保持健康。这证实了通过 DSM 估计混合分数能为生成器提供稳健的信号。

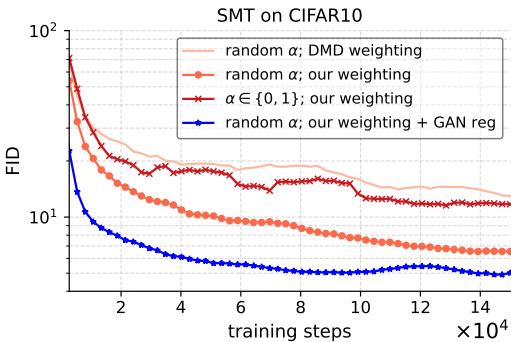
此外，观察训练过程中的 FID 演变可以看出，该方法随着时间的推移持续提高样本质量，没有出现对抗性训练中常见的 erratic 行为。

视觉质量

数据很好看，但图像效果如何呢？

以下是 SMT 模型 (从头训练) 在 ImageNet 上的样本。对于一个不依赖预训练骨干网络的单步模型来说，其多样性和保真度都非常出色。

以下是 SMD 模型 (蒸馏) 在 CIFAR-10 上的样本。图像清晰，与训练数据难以区分。

潜在空间插值

一个好的生成模型不应该只是死记硬背训练数据；它应该学习一个有意义的潜在空间。作者通过在随机噪声向量之间进行插值来证明了这一点。

在 图 6 中，你可以看到不同图像之间的平滑过渡 (例如，顶行的狗改变姿势) 。这表明生成器已经学习了数据流形的结构化且连续的表示。

结论

“混合分数 (Score-of-Mixture) ”框架代表了生成建模向前迈出的重要一步。它成功地将高质量样本的生成与迭代扩散过程的计算负担解耦，同时也没有屈服于 GANs 的不稳定性。

主要收获:

• 简单性: SMT 使用分数估计直接最小化统计散度 (\(\alpha\)-JSD) 。
• 稳定性: 通过利用去噪分数匹配，它避免了对抗性极小极大优化的陷阱。
• 灵活性: 它既适用于从头训练 (SMT) ，也适用于蒸馏重型预训练模型 (SMD) 。
• 性能: 它在标准基准测试中实现了最先进或极具竞争力的单步生成结果。

对于学生和研究人员来说，这篇论文在信息论 (散度) 的几何洞察与现代基于分数的深度学习的实践力量之间架起了一座桥梁。它表明，快速生成的未来可能不需要新的架构，而是需要更好地理解我们如何比较和混合概率分布。