在机器学习理论的世界里，二分类和三类及以上分类之间往往存在着明显的差异。虽然我们在各个领域都能看到这种情况，但最近一篇题为 “Statistical Query Hardness of Multiclass Linear Classification with Random Classification Noise” (随机分类噪声下多类线性分类的统计查询困难性) 的论文，凸显了在从噪声数据中学习时，两者在复杂度上的巨大鸿沟。

多类线性分类 (Multiclass Linear Classification, MLC) 是教科书式的经典问题: 给定高维空间中的数据点，我们能否找到线性边界将它们分为 \(k\) 个不同的类别？当标签是干净的 (完全准确) 时，我们可以有效地解决这个问题。但当我们引入 随机分类噪声 (Random Classification Noise, RCN)——即标签根据噪声矩阵随机翻转时——情况就变得复杂了。

对于二分类 (\(k=2\)) ，我们在几十年前就知道，即使有噪声，我们也能有效地解决这个问题。然而，这项新研究抛出了一枚重磅炸弹: 一旦增加到 \(k=3\) (三类) ，对于一类被称为统计查询 (SQ) 算法的广泛算法而言，这个问题在计算上变得极其困难。

在这篇深入的文章中，我们将拆解这一结果背后的数学原理和直觉。我们将探讨研究人员如何构建一个特定的“陷阱”——一种数据和噪声的分布，除非你确切知道去哪里寻找，否则它看起来在统计上与纯噪声一模一样。

问题: 带噪声的多类线性分类

让我们定义一下设置。我们要学习一个分类器 \(f : \mathbb{R}^d \to [k]\) (其中 \([k] = \{1, \dots, k\}\)) 。在线性情况下，分类器由 \(k\) 个权重向量 \(w_1, \dots, w_k\) 定义。输入 \(x\) 被分配给使点积 \(w_i \cdot x\) 最大的标签 \(i\)。

在现实世界中，标签很少是完美的。 随机分类噪声 (RCN) 模型对此进行了形式化。我们假设存在一个“真实”分类器 \(f^*\)。然而，学习者永远看不到真实的标签 \(y^* = f^*(x)\)。相反，他们看到的是一个受损的标签 \(y\)。

这种破坏由一个噪声矩阵 \(H \in [0, 1]^{k \times k}\) 控制。如果真实标签是 \(i\)，观察到的标签变为 \(j\) 的概率为 \(H_{ij}\)。

在二分类情况 (\(k=2\)) 下，像感知机 (Perceptron) 或修正的支持向量机 (SVM) 这样的算法可以有效地处理这种噪声。噪声虽然有效地“压缩”了信号，但并没有破坏分离超平面的方向。这篇论文的研究人员提出了一个问题: 这种好运在 \(k \ge 3\) 时还能延续吗?

答案是明确的: 不能 。

SQ 模型与困难性

为了证明一个问题是“困难的”，理论计算机科学家经常使用 统计查询 (SQ) 模型 。

在标准的机器学习中，算法观察单个样本 \((x, y)\)。而在 SQ 模型中，算法不允许查看单个样本。相反，它必须查询关于分布的统计属性。例如，算法可能会问: “\(x_1 y\) 的平均值是多少？”或者“\(x_2 > 0\) 且 \(y=1\) 的概率是多少？”。预言机 (Oracle) 会以一定的容差 \(\tau\) 回答这些查询。

我们为什么关心 SQ 困难性？因为我们使用的几乎所有标准算法——梯度下降、期望最大化 (EM)、主成分分析 (PCA)、标准矩方法——都可以作为 SQ 算法来实现。如果一个问题是 SQ 困难的，这意味着几乎所有标准技术都无法有效地解决它。

该论文证明，对于 \(k \ge 3\) 的带 RCN 的 MLC 问题，SQ 算法需要 超多项式复杂度 (super-polynomial complexity) 。 简单来说: 随着数据维度的增加，计算成本爆炸式增长，以至于问题实际上变得无法解决。

核心方法: 构建不可能的分布

这篇论文的核心是一个构造性证明。作者创建了一个特定的“最坏情况”场景，这在技术上是一个多类线性分类问题，但在统计上与随机噪声无法区分。

为了实现这一点，他们将 学习 (Learning) 问题归约为 假设检验 (Hypothesis Testing) 问题。

1. 归约为假设检验

学习的目标是找到一个误差接近最优误差 (\(\text{opt}\)) 的假设 \(\hat{h}\)。作者定义了一个相关的 相关性检验问题 (Correlation Testing Problem) 。

算法面对一个分布 \(D\)，被要求在两种现实之间做出决定:

1. 零假设 (Null Hypothesis): 标签 \(y\) 的生成完全独立于 \(x\)，遵循基于噪声矩阵行 \(h_k\) 的固定分布。 (纯噪声) 。
2. 备择假设 (Alternative Hypothesis): 标签 \(y\) 是由特定的带 RCN 的 MLC 实例生成的。 (存在信号) 。

如果算法不能有效地无法区分这两种情况，它当然也无法学习分类器。如果数据对算法来说看起来像纯噪声，它就无法找到决策边界。

检验逻辑依赖于假设的误差分解。对于多类假设 \(h\)，误差可以写成:

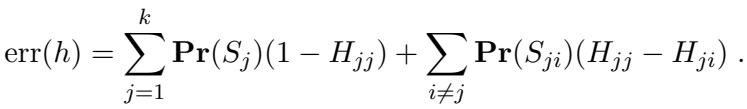
这里，\(S_j\) 是真实标签为 \(j\) 的区域。关键的见解是，如果我们能创造一种情况，使得“备择”假设下 \(y\) 的边缘分布看起来与“零”假设完全一样，算法就会感到困惑。

具体来说，他们寻找一个条件，即噪声矩阵的最后一行 \(h_k\) 是其他行的 凸组合 (convex combination) 。 这是数学上的“伪装”。如果第 \(k\) 类的噪声轮廓看起来像是第 \(1\) 到 \(k-1\) 类噪声轮廓的混合物，算法就很难分辨它看到的是第 \(k\) 类还是其他类的混合。

从数学上讲，如果我们满足这个条件，看到标签 \(y=i\) 的概率表现如下:

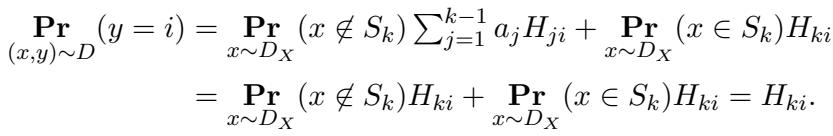
这个等式本质上是说: “无论我们是否在区域 \(S_k\) 中，看到标签 \(i\) 的概率都是 \(H_{ki}\)。”这在边缘分布层面上完全掩盖了 \(x\) 和 \(y\) 之间的依赖关系。

2. 隐藏方向分布

为了使检验问题变得困难，作者使用了一种涉及 隐藏方向分布 (Hidden Direction Distributions) 的技术。

他们假设数据 \(x\) 在所有方向上都是标准高斯分布，除了一个特定的、秘密的方向 \(v\)。沿着这个方向 \(v\)，数据遵循一个精心设计的 一维分布 \(A\)。

• 在与 \(v\) 正交的方向上，数据是高斯噪声。
• 标签 \(y\) 仅取决于投影 \(v \cdot x\)。

SQ 算法需要“找到” \(v\)。但是，如果一维分布 \(A\) 看起来与高斯分布非常相似 (就其统计矩而言) ，算法就必须搜索指数级数量的方向，才能找到那个数据不仅仅是高斯噪声的方向。

3. “尖峰状”边缘分布

这就是构造变得巧妙的地方。作者需要沿着这条一维线为不同的类别 (\(S_1, S_2, \dots\)) 定义区域。

他们定义了分布 \(A_1, \dots, A_{k-1}\)，分别对应于真实标签为 \(1, \dots, k-1\) 时的数据分布。

• 这些分布支撑在不相交的区间上 (因此类别是可分的) 。
• 关键是，它们匹配标准高斯分布的前 \(m\) 阶矩。

下图展示了 \(k=3\) 时的情况。

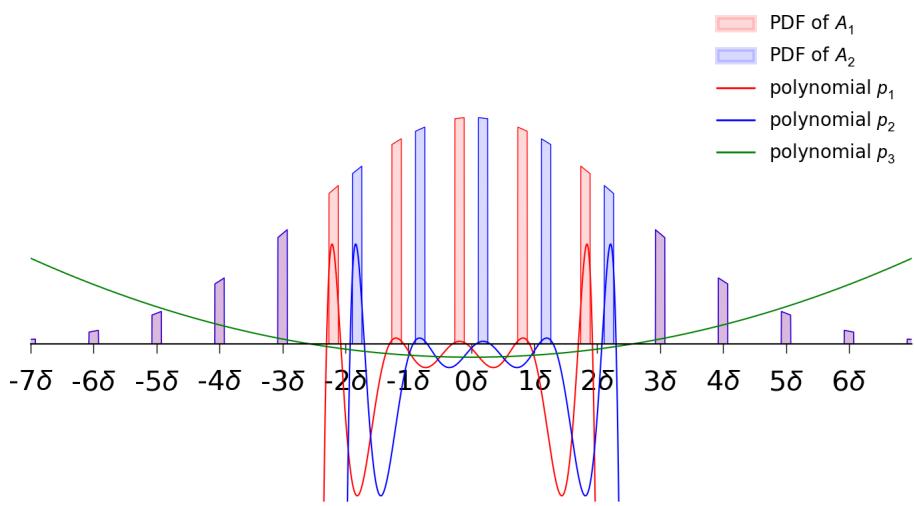
在图 1 中，注意那些“尖峰” (区间) 。红色区间 (\(J_1\)) 是真实标签为 1 的地方。蓝色区间 (\(J_2\)) 是真实标签为 2 的地方。其他地方 (间隙) 的真实标签是 3。

作者通过取一个高斯分布并将其切成区间来构建这些分布 \(A_i\)。

• \(A_1\) 在一组区间上为正，在其他地方为零。
• \(A_2\) 是 \(A_1\) 的平移版本。
• 在这些区间并集 (\(I_{in}\)) 之外，分布是相同的。

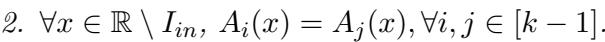
通过精心选择这些区间的宽度和间距，他们确保 \(A_1\) 和 \(A_2\) 的矩与标准高斯几乎完全相同。这意味着简单的统计数据 (均值、方差、偏度等) 无法区分这种“尖峰状”分布和平滑的高斯钟形曲线。

4. 混合信号

拼图的最后一块是这些基础分布如何转化为观察到的噪声数据。

回想一下“伪装”条件: 噪声矩阵的第 \(k\) 行是其他行的混合。当我们观察以 观察到的 标签 \(y=i\) 为条件的数据分布时，我们得到的是一个混合分布。

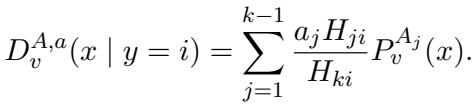
因为基础分布 \(A_j\) 是矩匹配高斯分布的，所以它们的任何混合 也 是矩匹配高斯分布的。

下图可视化了条件分布 \(D|_{y=1}, D|_{y=2}, D|_{y=3}\)。即使真实区域是截然不同的 (图 1 中的红/蓝尖峰) ，以噪声标签为条件的 观察 分布却有显著重叠，并且看起来“像高斯一样”。

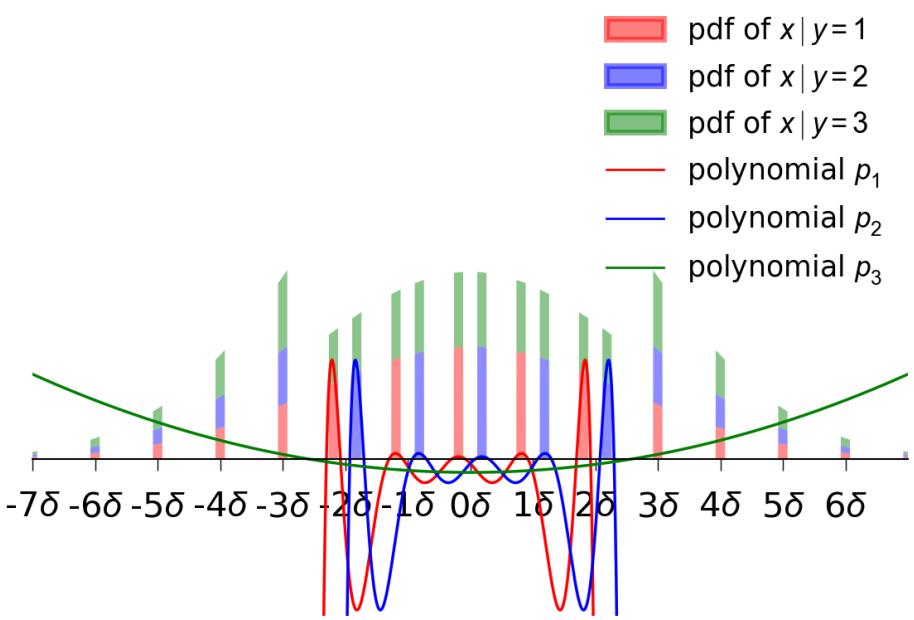
因为这些条件分布匹配高斯分布的矩，它们相对于高斯分布的 成对相关性 (pairwise correlation) 极小。

成对相关性的数学界限依赖于卡方散度:

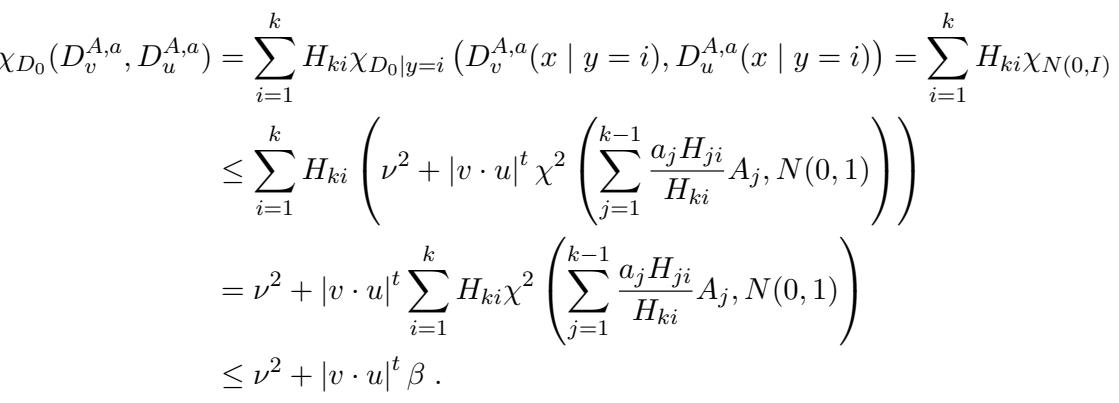
这个推导 (式 29) 本质上证明了构建的噪声分布与纯噪声之间的统计“距离”是微小的 (\(\tau\))。在 SQ 模型中，如果相关性被 \(\beta\) 界定，且所需的查询容差为 \(\tau\)，则所需的查询次数与相关性的倒数成比例。由于相关性呈指数级小 (归功于匹配了许多矩) ，复杂度变得超多项式级。

实验与结果: 困难性定理

论文提出了三个主要的理论结果，逐步关上了 MLC 带 RCN 问题高效算法的大门。

结果 1: 学习到 opt + ε 的困难性 (k=3)

第一个结果针对的是标准的学习目标: 找到一个误差接近最优可能误差 (\(\text{opt}\)) 的分类器。

作者构建了一个特定的 \(3 \times 3\) 噪声矩阵 \(H\):

注意第三行 \((0.3, 0.3, 0.4)\) 正好是前两行的平均值: \(\frac{1}{2}(0.6, 0, 0.4) + \frac{1}{2}(0, 0.6, 0.4)\)。这完美地满足了凸组合条件。

定理: 对于这个矩阵，任何学习到误差为 \(\text{opt} + \epsilon\) 的 SQ 算法都需要超多项式时间 (具体为 \(d^{\tilde{\Omega}(\log d)}\)) 。

这个结果令人震惊，因为噪声率之间的间隔 (\(\min |H_{ii} - H_{ij}|\)) 是一个常数 (\(0.1\))。即使噪声分离良好，\(k=3\) 的结构也允许这种“伪装”效应隐藏真实的分类器。

结果 2: 近似的困难性

也许我们不需要最优误差。我们能不能只得到一个“足够好”的分类器？也许是在最优误差的一个常数倍以内？

作者将构造推广到了更大的 \(k\)。他们设计了一个 \(k \times k\) 矩阵，其中最后一行是前 \(k-1\) 行的平均值。

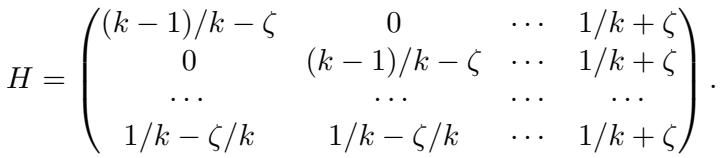
定理: 对于任何常数 \(C > 1\)，存在一个噪声矩阵 (其中 \(k \approx C\)) ，使得找到一个误差为 \(C \cdot \text{opt}\) 的分类器是 SQ 困难的。

这扼杀了高效近似算法的希望。随着类别数量的增加，问题不仅变得难以完美解决；它变得根本难以解决。

结果 3: 难以超越随机猜测

棺材上的最后一颗钉子是“随机猜测”下界。如果你有 \(k\) 个类别并且你均匀随机地猜测，你的误差是 \(1 - 1/k\)。我们至少能做得比这更好吗？

论文表明，对于大的 \(k\) 和特定的噪声矩阵 (其中对角线上的“信号”很弱，\(O(1/poly(d))\)) ，生成一个误差优于 \(1 - 1/k\) 的假设是 SQ 困难的。

启示: 在这些噪声多类设置中，如果依赖标准的统计查询，复杂的算法可能并不比简单的随机猜测器表现得好多少。

结论

这篇论文对多类分类的复杂性进行了发人深省的审视。它揭示了一个根本性的不连续性:

• 二分类 (\(k=2\)): 噪声很讨厌，但是可解的。单个超平面的几何结构足够稳健，RCN 无法完全掩盖信号。
• 多类分类 (\(k \ge 3\)): 噪声可以模仿信号。多个决策边界与特定噪声矩阵之间的几何相互作用，允许一个类别的“噪声”分布完美地模拟另一个类别 (或它们的混合) 的分布。

作者证明了 带随机分类噪声的多类线性分类是 SQ 困难的 。 这表明，在不假设数据分布或噪声矩阵结构具有更强条件的情况下，对于一般情况下的这个问题，不存在高效的、抗噪声的算法。

对于学生和从业者来说，这强调了一个至关重要的教训: 来自二分类的直觉并不总能推广。从 2 到 3 的跨越不仅仅是数字的增加；它是结构复杂性的飞跃。在处理带噪声的多类数据时，标准的线性方法可能会失败，不是因为代码写错了，而是因为问题本身在根本上就是困难的。