引言: 长上下文注意力的悖论

Transformer 架构彻底改变了自然语言处理领域，但它隐藏着一个众所周知的秘密: 在大规模应用时效率极其低下。罪魁祸首就是自注意力机制 (Self-Attention) 。在标准形式下，序列中的每一个 token 都要关注其他所有的 token。如果你将输入文档的长度加倍，计算成本不仅仅是加倍——而是变为原来的四倍。这就是臭名昭著的 $O(n^2)$ 复杂度。

多年来，研究人员都知道这种密集 (dense) 注意力通常是浪费的。当你阅读一本书时，你不会为了理解当前的句子而同时关注每一页上的每一个词。你会关注几个关键的上下文线索。用机器学习的术语来说，注意力概率分布通常是 稀疏的 (sparse) ——在少数相关的 token 上出现峰值，而其余部分则是接近于零的噪声。

虽然数学上优雅的“稀疏注意力”机制 (如 $\alpha$-entmax) 可以将这些噪声归零，但它们面临着一个实际的悖论: 在 GPU 上实现它们通常会让模型变慢，而不是变快。 标准硬件针对密集矩阵乘法进行了优化，而弄清楚忽略什么所需的逻辑，通常比直接计算所有内容还要耗时。

ADASPLASH 应运而生。

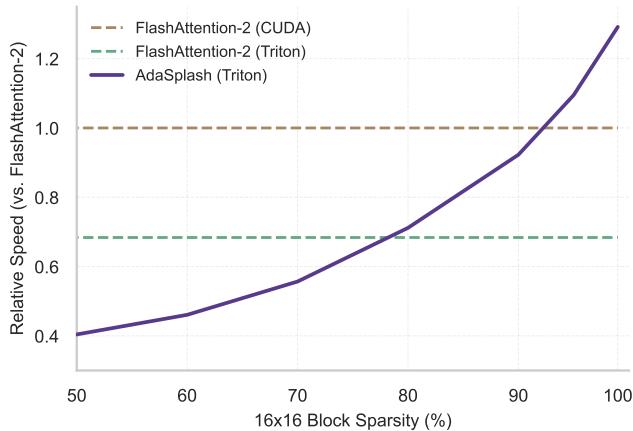
图 1. 非因果注意力运行时间 (Fwd+Bwd) 与输入稀疏度的函数关系。虽然高度优化的 FlashAttention-2 在不同稀疏度水平下保持恒定的运行时间，但 ADASPLASH 有效地利用了稀疏性来获得加速，最终随着稀疏度的增加优于 FlashAttention-2。

如图 1 所示，ADASPLASH 是一种新的算法和硬件实现，它终于将稀疏性的理论优势与硬件现实结合了起来。与以往稀疏性反而成为计算负担的方法不同，ADASPLASH 实际上随着注意力变得越稀疏而越快，最终甚至超越了高度优化的 FlashAttention-2。

在这篇文章中，我们将解构 ADASPLASH 论文。我们将探讨“真正”稀疏性背后的数学原理、用于高效计算的算法技巧，以及允许 Transformer 跳过噪声并专注于重要内容的自定义 GPU 内核。

1. 背景: Softmax 的问题

要理解为什么需要 ADASPLASH，我们首先需要看看标准的注意力机制。Transformer 的核心是点积注意力 (dot-product attention) :

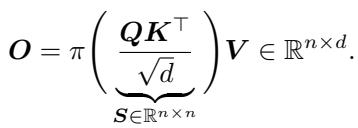
$()\nO = \\pi \\bigg ( \\underbrace { \\frac { Q K ^ { \\top } } { \\sqrt { d } } } _ { S \\in \\mathbb { R } ^ { n \\times n } } \\bigg ) V \\in \\mathbb { R } ^ { n \\times d } .\n[$

这里，$Q, K, V$ 分别是查询 (Query) 、键 (Key) 和值 (Value) 矩阵。函数 $\pi$ 通常代表 softmax 变换。

Softmax 问题

Softmax 旨在将分数转换为总和为 1 的概率。然而，softmax 有一个特殊的性质: 它永远不会产生零值。 即使一个 token 完全不相关，softmax 也会给它分配一个微小的非零概率 (例如 $0.00001$) 。

在短序列中，这可以忽略不计。但在长序列 (例如 32k 或 100k token) 中，成千上万个微小的数值累积起来会导致两个问题:

噪声: 相关的信号被无关 token 的“长尾”稀释了。
计算浪费: GPU 必须加载并计算每一个 token 对的交互，即使是那些无关紧要的。

硬件瓶颈

最近, FlashAttention 彻底改变了我们计算标准注意力的方式。它认识到瓶颈不仅仅是算术运算 (FLOPs) ，还有内存带宽 (HBM 读/写) 。FlashAttention 通过“分块 (tiling) ”计算解决了这个问题——将 $Q, K, V$ 的小块加载到快速的片上 SRAM 中，计算注意力，然后只写回结果，而无需在慢速内存中显式生成巨大的 $N \times N$ 注意力矩阵。

然而，FlashAttention 假设的是密集的 softmax。如果我们想使用稀疏注意力来节省时间，我们需要一种方法在数学上将概率强制为零，并需要一个知道如何高效跳过这些零的硬件内核。

2. 数学基础: $\alpha$-entmax

为了用允许零值的东西替代 softmax，作者利用了 $\alpha$-entmax 变换。这是 softmax 的一种推广，它将分数向量映射到概率分布，但有一个关键的区别: 它是稀疏的。

$]\n\\alpha \\mathrm { - e n t m a x } \\left( s \\right) = \\left[ ( \\alpha - 1 ) s - \\tau \\mathbf { 1 } \\right] _ { + } ^ { 1 / \\alpha - 1 } ,\n[$

在这个方程中:

$[\cdot]_+$ 是 ReLU 函数 (保持数值为正) 。
$\tau$ 是一个归一化阈值。
$\alpha$ 控制稀疏性。
如果 $\alpha \to 1$，它的行为像 softmax (密集) 。
如果 $\alpha = 2$，它就变成了 sparsemax , 这是高度稀疏的。
中间值 (例如 $\alpha = 1.5$) 提供了一种平衡。

关键的结论是，如果分数 $s_i$ 足够低 (具体来说，如果 $(\alpha - 1)s_i \le \tau$) ，概率将变为 精确的零 。

计算障碍

理想情况下，我们只需应用这个公式。但有一个陷阱: 我们不知道 $\tau$。必须精确选择阈值 $\tau$，使得产生的概率之和正好为 1。找到 $\tau$ 需要找到该方程的根:

$]\nf ( \\tau ) = \\sum _ { i } \\left[ ( \\alpha - 1 ) s _ { i } - \\tau \\right] _ { + } ^ { 1 / ( \\alpha - 1 ) } - 1 .\n[$

我们需要找到使 $f(\tau) = 0$ 的 $\tau$。这是一个隐式方程，必须对注意力矩阵的每一行进行迭代求解。如果这个求解过程很慢，整个注意力机制就会比标准 softmax 还要慢，这就违背了初衷。

3. 创新点 1: 混合 Halley-Bisection 算法

现有的实现通常使用 二分法 (Bisection) 算法来查找 $\tau$。二分法的工作原理是定义一个范围 (下界和上界) 并反复将其减半。

$]\nB _ { f } ( \\tau ) = \\left{ \\begin{array} { l l } { ( \\tau _ { \\mathrm { l o } } , \\tau ) } & { \\mathrm { i f ~ } f ( \\tau ) < 0 , } \\ { ( \\tau , \\tau _ { \\mathrm { h i } } ) } & { \\mathrm { o t h e r w i s e } , } \\end{array} \\right.\n[$

虽然可靠，但二分法是线性收敛的。它需要多次迭代才能获得精确值。在高速 GPU 内核中，每次迭代都会消耗宝贵的周期来读取数据。

Halley 法

为了加速这一过程，作者建议使用 Halley 法 (Halley’s Method) 。与盲目将范围减半的二分法不同，Halley 法利用曲线的斜率 (导数) 和曲率 (二阶导数) 信息，对零点位置做出有根据的猜测。

更新规则如下所示:

$]\nH _ { f } ( \\tau ) = \\tau - \\frac { 2 f ( \\tau ) f ^ { \\prime } ( \\tau ) } { 2 f ^ { \\prime } ( \\tau ) ^ { 2 } - f ( \\tau ) f ^ { \\prime \\prime } ( \\tau ) } ,\n[$

获得导数的计算成本很低，因为它们只是对输入分数的求和:

$]\n\\begin{array} { l } { { f ^ { \\prime } ( \\tau ) = - { \\displaystyle \\frac { 1 } { \\alpha - 1 } } \\sum _ { i } \\left[ ( \\alpha - 1 ) s _ { i } - \\tau \\right] _ { + } ^ { 1 / ( \\alpha - 1 ) - 1 } , } } \\ { { f ^ { \\prime \\prime } ( \\tau ) = { \\displaystyle \\frac { 2 - \\alpha } { ( \\alpha - 1 ) ^ { 2 } } } \\sum _ { i } \\left[ ( \\alpha - 1 ) s _ { i } - \\tau \\right] _ { + } ^ { 1 / ( \\alpha - 1 ) - 2 } . } } \\end{array}\n[$

混合方法

当 Halley 法奏效时，它的速度极快 (立方收敛) ，但如果初始猜测偏差太远，它可能会不稳定。为了兼顾两者的优点，作者引入了 混合 Halley-Bisection 算法。

尝试进行 Halley 更新。
检查新的 $\tau$ 是否落在当前有效范围内。
如果是，保留它 (快速跳跃) 。
如果否，回退到二分法步骤 (保证安全性) 。

结果是达到机器精度所需的迭代次数大幅减少。

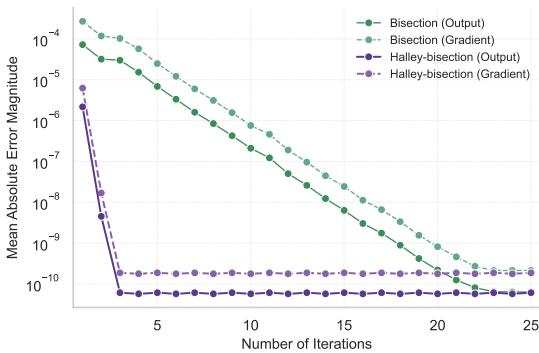
$图 2. Halley-bisection 与 Torch 的二分法在不同迭代次数下的平均绝对误差幅度比较，针对 \$\\alpha = 1.5\$ 的精确解进行测量$

如图 2 所示，基于 Halley 的方法 (紫色/红色线) 仅需几次迭代就将误差降至零，而标准二分法 (蓝色/橙色线) 则拖延得更久。

4. 创新点 2: ADASPLASH 内核

拥有快速的数学公式是一回事；让它在 GPU 上快速运行是另一回事。作者使用 Triton 实现了 ADASPLASH，这是一种专为编写高性能 GPU 内核而设计的语言。

核心策略反映了 FlashAttention 的思想: 分块 (Tiling) 。输入矩阵 $Q$ 和 $K$ 被分成块。这些块从 HBM (高带宽内存) 加载到 SRAM (快速缓存) 。

具有块稀疏性的前向传播

该算法按步骤进行:

分块计算 $\tau$: 函数 $f(\tau)$ 是可加的。这意味着我们可以计算不同 $K$ 块的部分和，并将它们聚合以找到阈值 $\tau$。

$]\nf ( \\pmb { \\tau } _ { i } ) = \\sum _ { j = 1 } ^ { T _ { c } } f ( \\pmb { \\tau } _ { i } ; \\pmb { S } _ { i } ^ { ( j ) } )\n[$

动态块掩码 (Dynamic Block Masking) : 这是一个颠覆性的改变。一旦为查询行块 ($Q_i$) 找到了近似的 $\tau$，算法就会检查哪些键块 ($K_j$) 实际上会导致非零概率。

如果一个块的注意力分数都低于阈值 $\tau$，则在 $\alpha$-entmax 之后整个块将为零。算法会在二进制掩码矩阵 $M$ 中标记这一点:

$]\nM _ { i j } = \\left{ \\begin{array} { l l } { 1 } & { \\mathrm { i f } \\ \\exists _ { i ^ { \\prime } \\in \\mathbb { Z } ( i ) , j ^ { \\prime } \\in \\mathcal { I } ( j ) } : S _ { i ^ { \\prime } , j ^ { \\prime } } > \\tau _ { i ^ { \\prime } } , } \\ { 0 } & { \\mathrm { o t h e r w i s e } , } \\end{array} \\right.\n[$

指针增量查找表: 利用掩码 $M$，ADASPLASH 构建了一个查找表。当计算最终输出 $O = PV$ 时，内核会查询这张表。

如果 $M_{ij} = 0$，内核会 跳过加载 值块 ($V_j$) ，并完全跳过矩阵乘法。
这实际上是根据数据动态地对计算进行剪枝。

反向传播 (训练)

训练需要计算梯度。ADASPLASH 将反向传播拆分为单独的内核以进行高效处理。它利用了 $\alpha$-entmax 函数 Jacobian 矩阵的稀疏性:

$]\n\\frac { \\partial \\alpha \\mathrm { - e n t m a x } ( s ) } { \\partial s } = \\operatorname { D i a g } ( \\pmb { u } ) - \\frac { \\pmb { u } \\pmb { u } ^ { \\top } } { \\Vert \\pmb { u } \\Vert _ { 1 } } ,\n[$

因为前向传播存储了块掩码 $M$ (或查找表) ，反向传播也可以跳过那些被归零的块的梯度计算。这在训练期间带来了巨大的节省。

$]\n\\begin{array} { l } { { \\displaystyle d { \\pmb Q } _ { i } = \\sum _ { j = 1 } ^ { n } U _ { i j } \\left( d P _ { i j } - \\delta _ { i } \\right) { \\pmb K } _ { j } } } \\ { { \\displaystyle d { \\pmb K } _ { j } = \\sum _ { i = 1 } ^ { n } U _ { i j } \\left( d P _ { i j } - \\delta _ { i } \\right) { \\pmb Q } _ { i } } } \\end{array}\n()$

如上面的梯度方程所示，计算仅在有效交互上迭代，忽略了稀疏零值。

5. 实验与结果

这种复杂的架构真的值得吗？作者在合成基准测试和现实世界的 NLP 任务中对 ADASPLASH 进行了测试。

效率基准测试

最引人注目的结果是运行时间的比较。

$图 3. 计算非因果注意力的算法效率，以越来越长的序列长度的平均训练步时间表示。我们对基于 \$\\alpha\$-entmax 的方法 (Bisection 和 ADASPLASH) 使用 \$\\alpha = 1.5\$。$

在图 3 中，请看紫线( AdaSplash (Triton) )。

可扩展性: 虽然标准 PyTorch 实现 (蓝色) 在 8k 序列长度时就会因内存溢出 (OOM) 而崩溃，但 ADASPLASH 可以优雅地扩展到 64k。
速度: 在高稀疏度水平下，它明显快于标准的 FlashAttention-2 (Triton 实现) 。请注意，标准 FlashAttention (CUDA) 在短序列上稍快，因为它是高度优化的 C++ 代码，但随着序列长度 (以及稀疏度) 的增加，ADASPLASH 缩小了差距并最终获胜。

现实世界性能

光快还不够；模型还必须准确。研究人员将 ADASPLASH 集成到了 RoBERTa、ModernBERT 和 GPT-2 中。

检索任务 (BEIR)

对于单向量检索，识别准确的相关信息至关重要。稀疏注意力在此大放异彩。

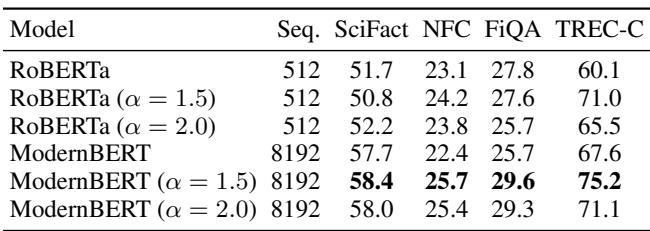
表 1. 单向量检索模型在 BEIR 基准测试不同任务上的结果 (nDCG@10)

ModernBERT 配合 $\alpha=1.5$ (使用 ADASPLASH) 始终优于密集的 ModernBERT 基线。稀疏性可能有助于模型过滤掉检索文档中的噪声。

长文档分类

在 ECtHR 数据集 (法律判决预测) 上，处理长上下文的能力至关重要。

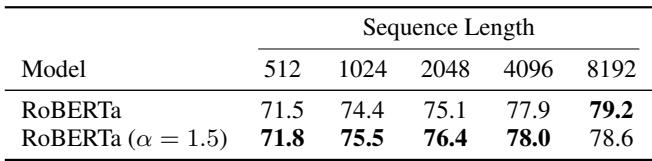
$表 2. 使用 softmax 和 \$\\alpha\$-entmax 注意力的长文档分类性能 (\$F_1\$ micro)。$

ADASPLASH (RoBERTa $\alpha=1.5$) 达到或超过了标准 RoBERTa 的性能，特别是在较长序列长度 (8192) 下。

关键是，看看资源使用情况:

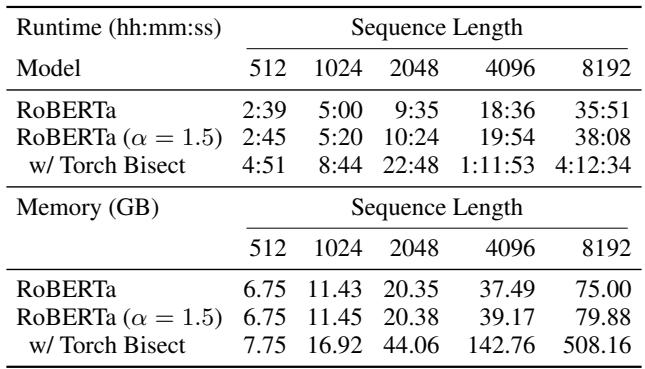
表 3. 长文档分类的每 epoch 运行时间 (时:分:秒) 和峰值内存使用量 (GB) …

标准二分法 (做稀疏注意力的旧方法) 在序列长度 8192 时，跑一个 epoch 需要 4 小时 12 分钟 。 ADASPLASH 只需要 38 分钟 。这是一个巨大的可用性差异。

语言建模 (GPT-2)

最后，在生成式建模 (GPT-2) 上的测试:

表 4. GPT-2 语言建模结果…

稀疏模型在 HellaSwag 上的验证损失和准确率均略优于密集基线，且运行时间和内存使用量几乎相同。

可视化稀疏性

模型真的学会变稀疏了吗？

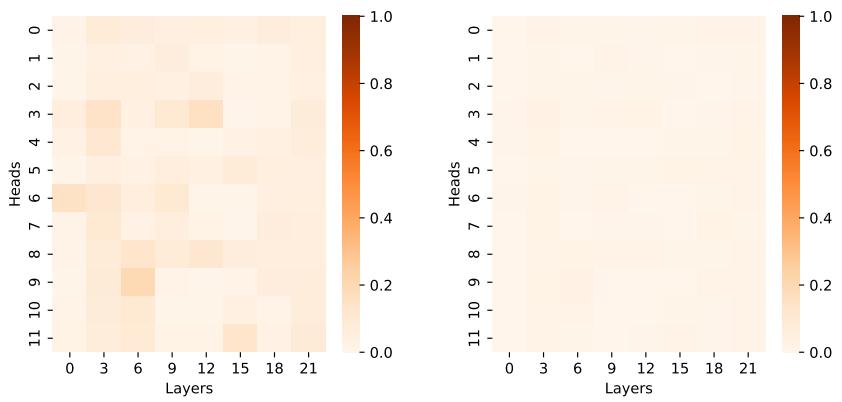
$图 4. GPT-2 的非零注意力分数比率 (\$\\alpha = 1.5\$)。$ $图 5. ModernBERT-base 非局部层的非零比率，\$\\alpha = 1.5\$ (左) 和 \$\\alpha = 2.0\$ (右) 。$

是的。上面的热图显示了非零分数的比率。在 ModernBERT (图 5) 中，我们看到了极高的稀疏性 (深红色表示高密度，浅色表示稀疏) 。许多注意力头仅有极少数活跃连接，证明 ADASPLASH 跳过的计算量确实是巨大的。

结论: 未来是稀疏的

ADASPLASH 论文代表了 Transformer 效率向前迈出的重要一步。多年来，社区都知道注意力是稀疏的——我们不需要看清一切才能理解某些东西。然而，我们的硬件 (GPU) 和软件 (密集内核) 迫使我们无论如何都要处理这些零。

ADASPLASH 通过以下方式打破了这个循环:

更快地解决数学问题: 使用混合 Halley-Bisection 算法快速找到稀疏阈值。
优化硬件: 使用带有块掩码的自定义 Triton 内核，从物理上跳过无关数据的计算。

其意义令人兴奋。通过消除稀疏注意力的计算惩罚，ADASPLASH 为在更长上下文上训练模型打开了大门，而无需庞大的 H100 集群。它将稀疏性从一种理论上的美好设想转变为一种实际的加速策略。

我们能让注意力机制既稀疏又快速吗？深入解读 ADASPLASH

引言: 长上下文注意力的悖论