在大型语言模型 (LLM) 飞速发展的宇宙中，模型的来源 (provenance) 已成为一个棘手的问题。随着每周有成千上万的模型涌现于 Hugging Face，一个关键问题随之而来: 这个模型究竟从何而来?

“SuperChat-7B” 究竟是从头开始训练的模型，还是仅仅给 Llama 2 换了个名字并做了微调？某家初创公司是真正创新出了一种高效架构，还是仅仅对一个更大的模型进行了剪枝？

这不仅仅是学术上的好奇心。它对知识产权、版权执行和安全审计有着巨大的影响。如果一个模型是在严格的非商业许可下发布的，而另一家公司发布了一个“新”模型，且该模型实际上只是原始模型的权重排列版本，我们该如何证明这一点？

在一篇题为 “Independence Tests for Language Models” (语言模型的独立性测试) 的精彩论文中，来自斯坦福大学的研究人员提出了一个严格的统计框架来回答这些问题。他们不只是将模型权重视为数字，而是将其视为法医调查中的证据。

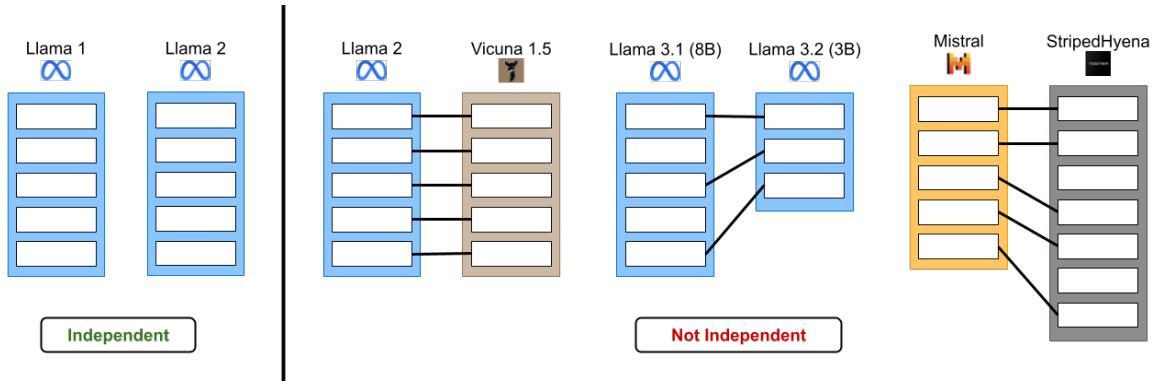
图示展示了各种大型语言模型 (LLM) 之间的独立关系。在左侧标记为“独立”的部分，两个 Llama 模型 (Llama 1 和 Llama 2) 显示为独立的实体，彼此之间没有连接。在中间部分，标记为“非独立”，Llama 2 通过线条连接到 Vicuna 1.5，表明存在相互依赖关系。再向右在“非独立”下方，Llama 3.1 (8B) 和 Llama 3.2 (3B) 之间有连接线，表示它们不是独立的。最后，在最右侧，Mistral 和 StripedHyena 通过多条线相互连接，加强了它们的非独立状态。

如图 1 所示，目标是区分真正独立的模型 (从不同的随机种子开始训练) 和那些共享血统的模型 (微调、剪枝或合并) 。

核心问题: 定义独立性

对于计算机而言，两个神经网络不过是两列巨大的数字 (参数) 。即使两个模型在完全相同的数据集上使用完全相同的架构进行训练，如果它们从不同的随机种子 (初始化) 开始，它们的最终权重看起来也会完全不同。

研究人员将其公式化为一个假设检验问题。 零假设 (\(H_0\)) 是这两个模型 \(\theta_1\) 和 \(\theta_2\) 是独立的。

\[ H _ { 0 } : \theta _ { 1 } \perp \theta _ { 2 } , \]

如果我们能以极低的 p 值 (例如 \(p < 0.05\) 或更低) 统计性地拒绝这一假设，我们就有了强有力的证据表明这些模型是相关的。

该论文在两种不同的设置下解决了这个问题:

  1. 受限设置 (The Constrained Setting) : 假设模型共享架构和标准的训练过程。
  2. 非受限设置 (The Unconstrained Setting) : 这是一个“狂野西部”般的场景，架构可能不同，或者对手主动试图隐藏模型的血统。

表 1: 受限设置与非受限设置的特征对比。

设置 1: 受限设置

假设你有两个在结构上看起来完全相同的模型——比如都是 Llama-7B 架构。你怀疑模型 B 是模型 A 的微调版本。

你可能会试图直接相减它们的权重并计算欧几里得距离 (L2 范数) 。如果距离很小，它们就是相关的，对吧？不一定。因为神经网络具有排列不变性 (permutation invariant) , 这种简单的距离度量会失效。

排列问题

在神经网络层中，神经元的顺序并不重要。你可以将第 5 个神经元与第 100 个神经元交换，只要你同时也交换下一层中对应的权重，函数的功能就会保持完全一致。

如果模型 B 是模型 A 的微调版，但开发者随机打乱了神经元以掩盖盗窃行为，简单的 L2 距离检查会显示巨大的差异，从而错误地提示它们是独立的。

解决方案: PERMTEST

研究人员提出了一种称为 PERMTEST 的测试方法。它利用了这样一个事实: 标准的训练算法 (如 SGD 或 Adam) 对所有神经元一视同仁——它们是“排列等变 (permutation equivariant) ”的。

直观理解如下:

  1. 取模型 A。
  2. 通过随机打乱模型 A 的隐藏单元来创建模型 A 的“伪”副本。在零假设下，这些副本在统计上与模型 A 是相同的。
  3. 比较模型 B 和模型 A。
  4. 比较模型 B 和模型 A 的那些“伪”打乱副本。

如果模型 B 真的独立于模型 A，那么它与模型 A 的相似度 (或不相似度) ，应该与它和那些打乱副本的相似度差不多。然而，如果模型 B 衍生自模型 A，那么它与模型 A 特定配置的距离可能会比与任何随机打乱版本的距离“近”得多。

证据: 来源热图

研究人员在“Llama 模型树”上评估了这种方法——这是一个包含 Vicuna、Alpaca 和其他衍生自 Llama 的开放权重模型的集合。

他们提出了两个强有力的统计量用于比较:

  1. \(\phi_{U}\) : 比较 MLP 的“上投影 (Up-projection) ”权重。
  2. \(\phi_{H}\) : 比较标准文本输入下的隐藏层激活 (神经元的输出) 。

结果令人震惊。下方是 \(\phi_{U}\) 统计量 (权重) 的热图。

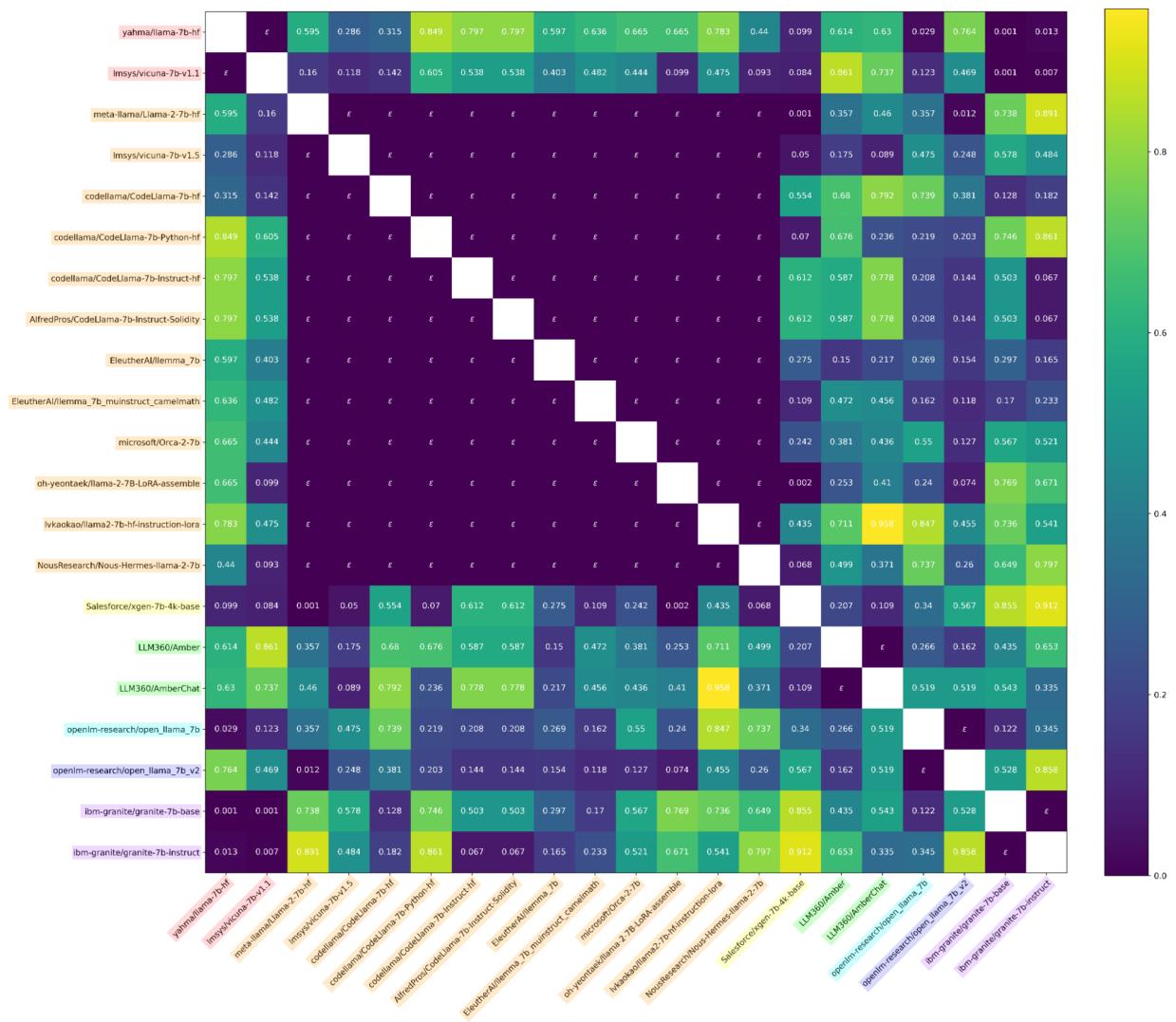
图 7: 我们报告了 Llama-7B 模型对的 \\(\\phi _ { U ^ { ( \\ell ) } }\\) p 值，其中 ε = 2.2e-308。我们在 \\(\\phi _ { U } ( \\ell )\\) 上使用 MATCH 并在 32 个 MLP 之间使用 FISHER 进行聚合。

在图 7 中，请看对角线。深色方块代表极低的 p 值 (统计显著性) 。这个矩阵正确地聚类了模型的“家族”。例如，所有 Llama-2 的衍生品都显示为依赖于 Llama-2，同时独立于原始的 Llama-1 或像 OpenLLaMA 这样不相关的模型。

他们还发现，比较激活 (模型“思考”的内容) 往往比比较权重更稳健。

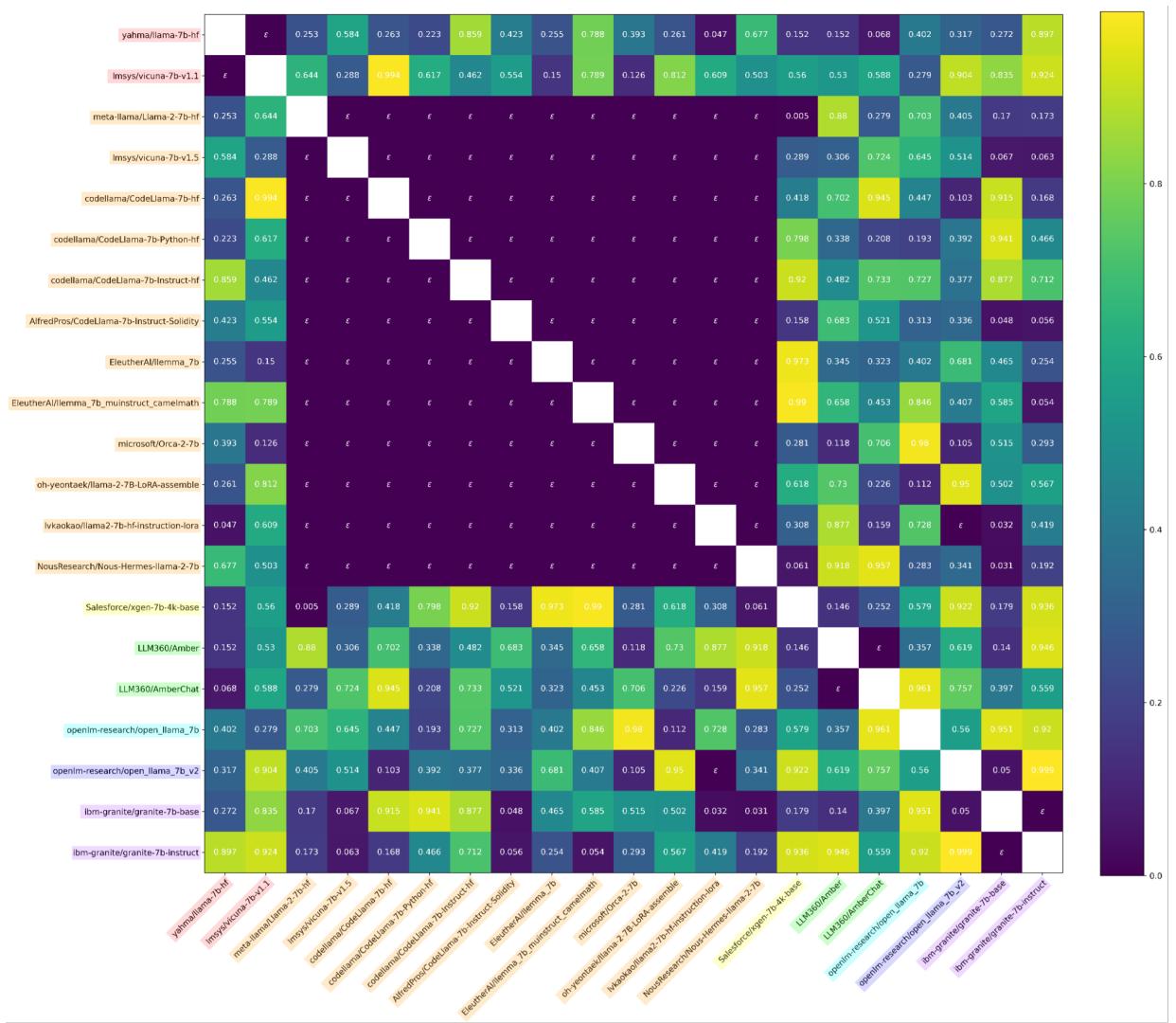
图 8: 我们报告了 Llama-7B 模型对的 \\(\\phi _ { H ^ { ( \\ell ) } }\\) p 值，其中 \\(\\varepsilon = 2 . 2 \\mathrm { { e } } { - 3 0 8 }\\)。我们在 \\(\\phi _ { H ^ { ( \\ell ) } }\\) 上使用 MATCH 并在 32 个 MLP 之间使用 FISHER 进行聚合。

在图 8 中，我们看到了使用激活的结果。独立 (亮黄/绿色) 与非独立 (深紫色) 之间的界限非常清晰。研究人员甚至能够通过这些测试确认，泄露的“Miqu-70B”模型确实是 Llama-2-70B 的量化版本。

设置 2: 非受限设置

受限设置虽然好用，但有一个弱点: 它假设我们知道架构，并且如果对手应用了 PERMTEST 未考虑的变换 (如特征空间的旋转) ，它就会失效。

如果窃贼稍微改变了模型架构怎么办？或者如果他们优化模型以掩盖踪迹呢？

鲁棒测试: MATCH + SPEARMAN

为了解决这个问题，作者引入了一种基于结构不变量 (structural invariants) 的鲁棒测试。他们特别关注门控线性单元 (GLU) MLP，这是几乎所有现代 LLM (Llama, Mistral 等) 都在使用的组件。

GLU MLP 有两个并行的线性层: 一个门 (Gate) 投影 (\(G\)) 和一个上 (Up) 投影 (\(U\))。它们进行逐元素相乘。

\[ f _ { \mathrm { m l p } } ( X _ { \mathrm { L N } _ { 2 } } ^ { ( i ) } ; \boldsymbol { \theta } _ { \mathrm { m l p } } ^ { ( i ) } ) = X _ { i } ^ { \mathrm { M L P } } = [ \sigma ( X _ { i } ^ { \mathrm { L N } _ { 2 } } \boldsymbol { G } _ { i } ^ { T } ) \odot ( X _ { i } ^ { \mathrm { L N } _ { 2 } } \boldsymbol { U } _ { i } ^ { T } ) ] D _ { i } ^ { T } \]

关键的洞察在于: 你不能在不以完全相同的方式排列上投影矩阵行的情况下，排列门矩阵的行 , 否则模型就会损坏。

研究人员设计了一个名为 \(\phi_{\text{MATCH}}\) 的统计量。

  1. 匹配 (Match) : 他们使用门矩阵 (\(G\)) 来寻找模型 A 和模型 B 之间的最佳对齐 (排列) 。
  2. 测试 (Test) : 他们将相同的对齐方式应用于上投影矩阵 (\(U\))。
  3. 相关性 (Correlate) : 他们计算对齐后的上投影矩阵的斯皮尔曼等级相关系数 (Spearman rank correlation) 。

如果模型是相关的，通过门矩阵找到的对齐应该也能完美对齐上投影矩阵。如果它们是独立的，基于门矩阵找到的对齐对于上投影矩阵来说就是随机噪声。

\[ \phi _ { \mathrm { M A T C H } } ^ { ( i , j ) } : = \mathtt { S P E A R M A N } \big ( \mathtt { M A T C H } \big ( H _ { \mathrm { g a t e } } ^ { ( i ) } \big ( \theta _ { 1 } \big ) , H _ { \mathrm { g a t e } } ^ { ( j ) } \big ( \theta _ { 2 } \big ) \big ) , \mathtt { M A T C H } \big ( H _ { \mathrm { u p } } ^ { ( i ) } \big ( \theta _ { 1 } \big ) , H _ { \mathrm { u p } } ^ { ( j ) } \big ( \theta _ { 2 } \big ) \big ) \big ) . \]

这个测试非常鲁棒。即使窃贼旋转模型权重或改变隐藏层维度大小，它仍然有效。

经验性的 “P值”

虽然这种方法不像 PERMTEST 那样产生理论上精确的 p 值，但经验表明它的行为方式与 p 值完全一致。

(a) \\(x \\in [ 0 , 1 )\\) 与独立模型对中 \\(\\phi _ { \\mathrm { M A T C H } } ^ { ( i ) }\\) 小于 \\(x\\) 的比例之图 (b) \\(x \\in [ 0 , 1 )\\) 与独立模型对中 \\(\\phi\\) MATCH (通过 FISHER 在所有 MLP 块上聚合) 小于 \\(x\\) 的比例之图

图 3 显示，对于独立模型 (零假设) ，该统计量的分布是均匀的 (蓝线沿着对角线) 。这意味着可以控制有效的假阳性率。

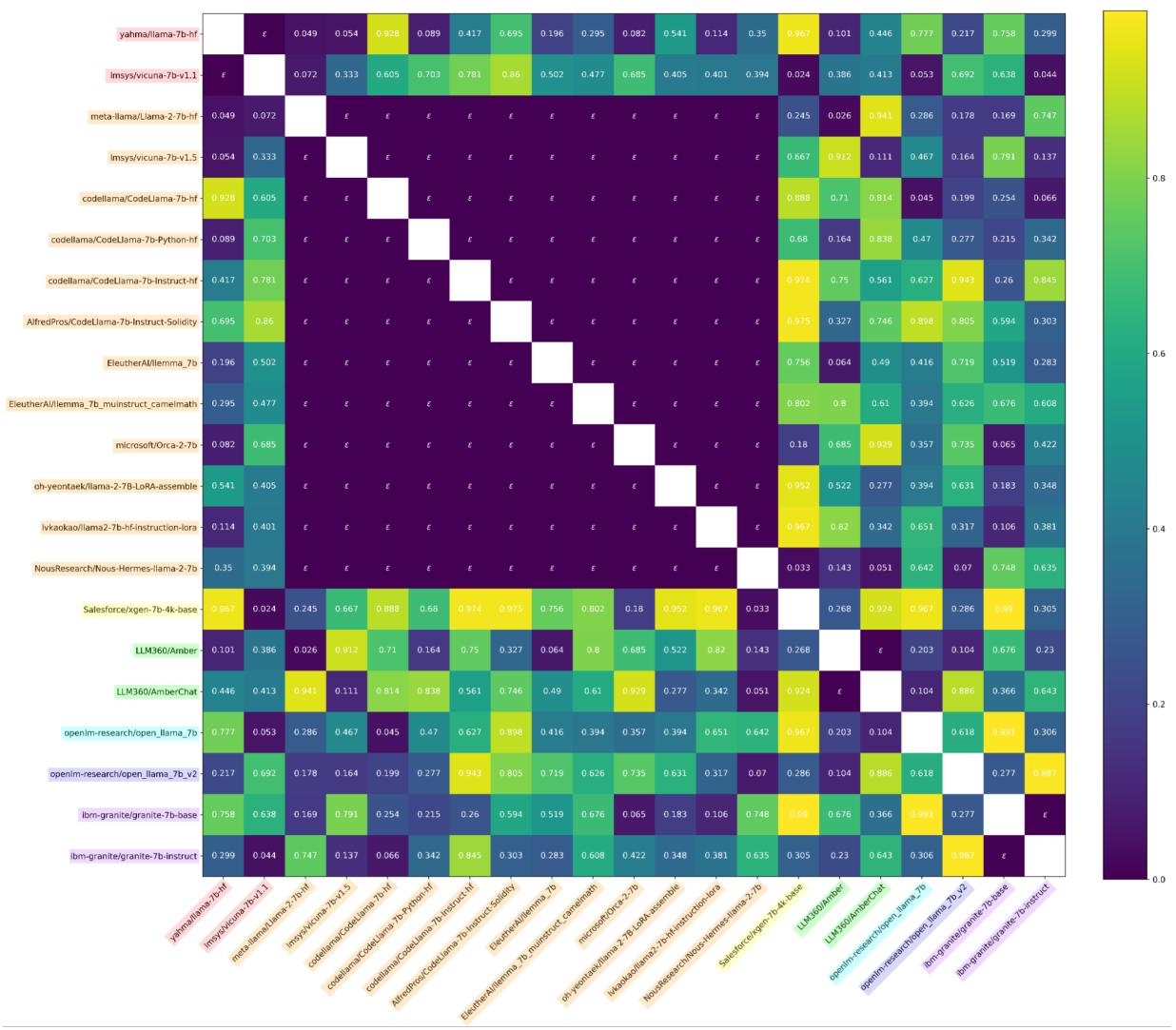
当应用于模型生态系统时，热图再次显示了对依赖模型的清晰检测，即使在对抗条件下也是如此。

图 9: 我们报告了 Llama-7B 模型对的 \\(\\phi\\) MATCH 值，其中 ε = 2.2e-308。我们在 \\(\\phi _ { \\mathrm { M A T C H } }\\) 上使用 MATCH 并在 32 个 MLP 之间使用 FISHER 进行聚合。

模型取证: Llama 3.2 案例

非受限测试最令人印象深刻的应用之一是局部测试 (Localized Testing) 。 因为 \(\phi_{\text{MATCH}}\) 对齐的是特定的层，所以它可以用来将一个模型的各个部分映射到另一个模型。

作者调查了 Llama 3.2 (3B) 。 Meta 报告称该模型是从 Llama 3.1 (8B) “剪枝 (pruned) ”而来的，意味着删除了层并剔除了神经元以使其更小。但是是哪些层？又是哪些神经元？

使用他们的测试，作者将 8B 模型的每一层与 3B 模型的每一层进行了匹配。

Llama3.1-8B

图 4 展示了这一发现。箭头准确显示了较大的 Llama 3.1 (顶部) 中的哪些层对应于较小的 Llama 3.2 (底部) 。你可以看到剪枝过程保留了早期层 (1-6) ，跳过了一些中间层，并保留了最后几层。这本质上是对 Meta 使用的剪枝配方进行了逆向工程。

此外，他们还分析了神经元维度是如何减少的。他们是直接砍掉了最后 6000 个神经元吗？

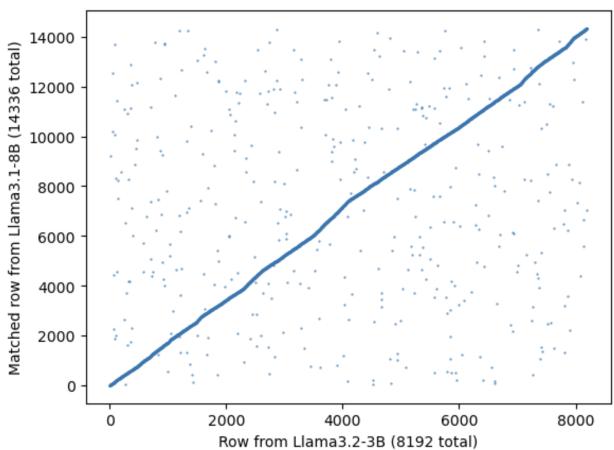
图 5: 我们使用 \\(\\mathsf { M A T C H } ( H _ { \\mathrm { u p } } ^ { ( \\ell ) } ( \\theta _ { 1 } ) , H _ { \\mathrm { u p } } ^ { ( \\ell ) } ( \\theta _ { 2 } ) )\\) 对齐 Llama 3.1-8B 和 Llama 3.2-3B 第一个 MLP 的上投影隐藏层激活，并在 x 轴上绘制 Llama 3.2-3B 的激活行，在 y 轴上绘制 Llama 3.1-8B 的匹配激活行。我们看到 Llama 3.2-3B 从 Llama 3.1-8B 剪枝得到的权重和激活很可能是均匀选择的。

图 5 绘制了匹配的神经元。x 轴是剪枝后的模型索引，y 轴是原始模型索引。强烈的对角线相关性意味着，虽然许多神经元被移除了，但保留下来的神经元在很大程度上保持了它们的相对顺序和结构。

战胜“强大”的对手

最后，论文解决了一个关键的反驳论点: “如果我重新训练这些层会怎样？”

如果一个小偷窃取了一个模型，但随即重新初始化 MLP 层，并在新数据上重新训练它们以匹配原始输出，权重的漂移难道不会大到足以逃避检测吗？

研究人员对此进行了模拟。他们取一个模型，剥离其 MLP 层，用随机权重替换它们，并重新训练它们以模仿原始模型的行为。

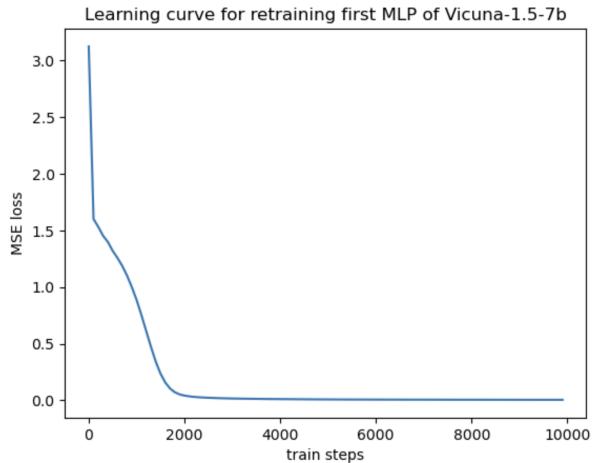
图 10: 我们展示了第 3.2.2 节中使用的 MLP 重训练实验 (重训练一个 MLP) 的学习曲线。

如图 10 所示，损失降至接近零——重新训练的层功能完美。然而，查看测试结果:

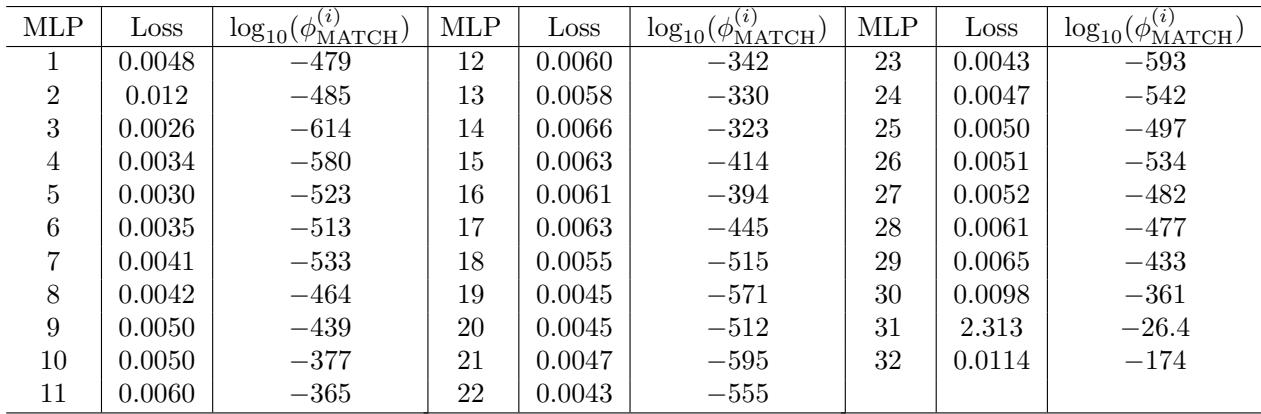
表 9: 我们重新训练 Llama-2-7b-hf 和 vicuna-7b-v1.5 的单个 MLP 块，然后使用算法 5 计算 \\(\\phi _ { \\mathrm { M A T C H } } ^ { ( i ) }\\)。即使在重新训练 MLP 层之后，\\(\\phi _ { \\mathrm { M A T C H } }\\) 仍然很小 (此处报告的是对数值) 。

表 9 显示，即使经过这种激进的重新训练，\(\phi_{\text{MATCH}}\) 统计量产生的 p 值仍像 \(10^{-479}\) 这样低。这些模型仍然被压倒性地识别为非独立。这表明计算的“形状”——处理数据所需的功能几何结构——将权重约束在一个特定的吸引域 (basin of attraction) 内，而独立性测试可以检测到这一点。

结论

开放权重的“狂野西部”正变得稍微有些秩序。这项研究表明，隐藏大型语言模型的血统比以前想象的要难得多。

无论是通过直接微调、剪枝，甚至是对抗性重训练，模型都会带有其祖先的统计指纹。通过利用神经网络的排列不变性以及像 GLU MLP 这样组件的结构约束，我们可以用数学上的确定性来追踪这些家族谱系。

这一工具包为开发者保护其知识产权，以及社区了解驱动我们 AI 未来的模型谱系，提供了一种强大的新方法。