石头、剪刀、LLM？为什么 AI 裁判会困惑以及如何修复它

如果你曾经尝试过给创意写作文章打分，你就会知道这有多主观。文章 A 比文章 B 好吗？也许吧。但是如果你把文章 B 和文章 C 比较，然后再把 C 和 A 比较，你可能会发现自己陷入了一个逻辑循环，每一篇文章似乎都在某些特定方面比上一篇更好。这就是非传递性 (non-transitivity) 的问题，事实证明，人工智能也深受其害。

随着像 GPT-4、Claude 和 Llama 这样的大型语言模型 (LLM) 变得越来越强，评估它们已成为一个巨大的瓶颈。我们不能再仅仅依赖人工标注——那太慢且太昂贵了。行业标准已经转向“LLM-as-a-Judge” (LLM 即裁判) ，即由一个强大的模型 (如 GPT-4) 充当老师，对其他模型的回答进行评分。

通常，这是通过将新模型与固定基线进行比较来完成的。但一篇名为*《Investigating Non-Transitivity in LLM-as-a-Judge》*的新论文揭示了这种方法的一个关键缺陷: LLM 裁判的表现很像是在玩“石头剪刀布”游戏。这种非传递性行为使得排行榜不稳定，排名也不可靠。

在这篇文章中，我们将深入探讨这项研究，探索为什么 LLM 裁判会感到困惑，“软性”非传递性背后的数学原理，以及旨在解决该问题的锦标赛式方案。

1. “黄金标准”问题

要理解这篇论文，我们首先需要了解现状。我们如何知道 Llama-3 是否比 Mistral-Large 更好？

对于开放式任务 (比如“写一首关于铁锈的诗”或“向蹒跚学步的孩子解释量子物理学”) ，没有单一的正确答案。你不能直接对答案。目前的行业标准是成对比较 (Pairwise Comparison) 。

固定基线框架 (The Baseline-Fixed Framework)

在像 AlpacaEval 这样的框架中，我们选取一个目标模型 (比如一个新的开源模型) 和一个固定的基线模型 (通常是旧版本的 GPT-4) 。我们将同一个提示词输入给两者，得到两个答案，然后让裁判 (GPT-4-Turbo) 选出胜者。

排名很简单: 对基线的胜率 (Win Rate against Baseline) 。

如果模型 A 击败基线的概率是 60%，而模型 B 击败基线的概率是 70%，我们就宣布模型 B 获胜。

隐藏的假设: 传递性

这种逻辑依赖于一个被称为传递性 (transitivity) 的数学属性。

  • 如果 模型 B > 基线
  • 且 基线 > 模型 A
  • 那么逻辑表明 模型 B > 模型 A。

如果这个假设成立，使用固定基线是高效且有效的。但如果不成立呢？如果模型 A 实际上在正面交锋中击败了模型 B，尽管它对基线的胜率较低，那该怎么办？

这就是研究的切入点。如下图所示，作者强调了“固定基线”方法的危险性，并对比了他们提出的解决方案 (循环赛) 。

固定基线框架与循环赛框架的对比。 图 1: 左侧，当偏好不一致时，固定基线框架会失效。右侧，循环赛捕捉到了全貌。

如果裁判认为 A 优于 B，B 优于 C，但 C 又优于 A，我们就得到了一个循环。如果你使用模型 B 作为基线，A 看起来像个输家 (因为 C 击败了 A，假设此处逻辑有误，原文意思应为: 在非传递性循环中，基线的选择决定了相对强弱) 。如果你使用模型 C 作为基线，A 看起来就像个赢家。 排名完全取决于你选择谁作为参考点。

2. 调查非传递性

研究人员着手量化这个问题的严重程度。他们研究了两种类型的非传递性: 硬性 (Hard) 和软性 (Soft) 。

硬性非传递性 (循环)

这是经典的逻辑违背。

\[ m _ { A } \succ m _ { B } , m _ { B } \succ m _ { C } , m _ { A } \prec m _ { C } \]
  • (其中 \(\succ\) 表示“击败”，\(\prec\) 表示“输给”) *

为了衡量这一点，作者定义了非传递性百分比 (PNT) 。 他们只是简单地统计数据中这些逻辑循环发生的频率。

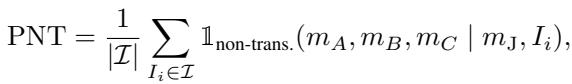
PNT 公式。

然而，LLM 很少给出二元的“是/否”。它们输出概率 (logits) 。一个模型可能 51% 确定 A 比 B 好。这就引出了第二种更微妙的错误。

软性非传递性

即使不存在严格的“循环”，偏好的幅度也可能是不一致的。

试想一下:

  1. 裁判认为 A 大幅 优于 B。
  2. 裁判认为 B 略微 优于 C。
  3. 传递性逻辑表明，裁判应该认为 A 大幅 优于 C。

如果裁判反而认为 A 只是勉强优于 C，那么偏好的“强度”就违反了传递性。为了捕捉这一点，作者引入了一个称为软性非传递性偏差 (SNTD) 的指标。

该指标使用 Jensen-Shannon 散度 (JSD) 来衡量实际观察到的胜率与模型完全符合逻辑时的预期胜率之间的距离。

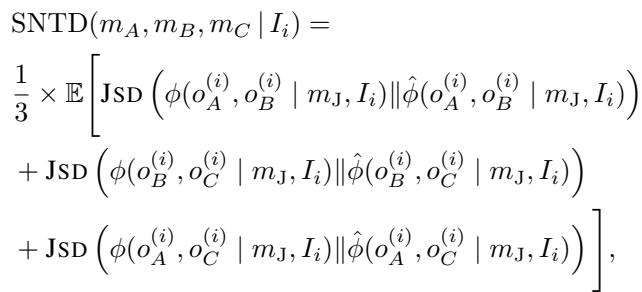
SNTD 公式。

确凿证据: 对基线的敏感性

那么，这真的会影响排名吗？作者进行了一项大规模实验，将 20 个不同的模型 (如 GPT-4o, Claude 3, Llama 3) 相互比较。

下面的热力图令人震惊。每一列代表使用不同模型作为基线 (行) 计算出的模型排名。如果传递性完全成立，无论你看哪一行 (基线) ，颜色 (排名) 应该大致一致。

显示对基线选择敏感性的排名热力图。 图 2: 列中不同的颜色表明，改变基线模型会显著改变目标模型的胜率和排名。

结果呢? 不一致。 例如，观察该图，胜率波动巨大，这取决于基线是 Llama-3-70B 还是 Claude-3-Opus。这证明了“对基线的胜率”是一个不稳定的指标。

3. 为什么裁判会困惑？

论文指出了导致这种非传递性行为的两个主要罪魁祸首: 模型相似性和位置偏差 。

“旗鼓相当”的问题

当被比较的模型能力相似时，非传递性达到峰值。当一个强模型对抗一个弱模型时，裁判通常是一致的。但是，当两个顶级模型 (如 GPT-4o 和 Claude 3 Opus) 对决时，裁判很难区分它们，从而导致充满噪音的循环偏好。

下面的热力图将其可视化。坐标轴代表模型之间的性能差距。注意明亮的黄色/绿色斑点 (高非传递性) 是如何聚集在中心 (原点) 周围的，那里的性能差距为零。

显示非传递性在原点附近达到峰值的热力图。 图 3: 当模型之间的性能差距很小 (接近原点) 时，非传递性变得严重。

位置偏差

LLM 有一个已知的偏差: 它们通常更喜欢看到的第一个答案 (有时是第二个) ，而不管质量如何。作者发现位置偏差是非传递性的一个主要驱动因素，特别是对于像 GPT-3.5 这样较弱的裁判而言。

位置偏差影响的条形图。 图 4: 与 GPT-4 (左) 相比，GPT-3.5 (右) 受位置偏差的影响很大。偏差缓解 (位置交换) 有所帮助，但不能完全解决问题。

作者尝试了“位置交换”——即交换答案顺序运行两次评估 (A vs B，然后 B vs A) 。虽然这有所帮助，但它并没有消除根本问题，即裁判的内部推理可能是循环的。

4. 解决方案: 锦标赛和 Bradley-Terry 模型

既然依赖单一基线是有缺陷的，作者提出了一种无基线 (Baseline-Free) 的方法。

步骤 1: 循环赛 (Round-Robin Tournaments)

在循环赛中，每个模型都要与其他所有模型进行对抗。如果你有 20 个模型，你需要对每一种可能的组合进行两两比较。这消除了对任何单一“参考”模型的依赖。

步骤 2: Bradley-Terry 模型

一旦我们要到了所有的比赛结果，我们该如何排名呢？我们不能只计算胜场数，因为击败一个强对手应该比击败一个弱对手更有价值。

作者使用了Bradley-Terry (BT) 模型 , 这是一种常用于体育排名的统计方法 (类似于 Elo) 。BT 模型假设模型 \(i\) 击败模型 \(j\) 的概率取决于它们潜在的“实力”分数 (\(\beta_i\) 和 \(\beta_j\)) 。

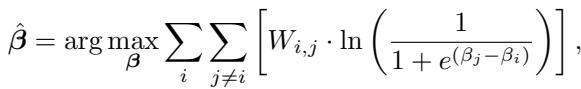
Bradley-Terry 系数最大化。

目标是找到一组实力分数 (\(\beta\)) ，使其最大化观测到的锦标赛结果的可能性。

一旦我们有了这些 \(\beta\) 系数，我们就可以将它们转换为 Elo 评级 , 这会给我们一个标准化的数字 (如 1200 或 1500) 来代表模型质量。

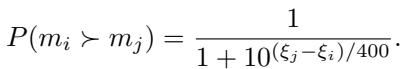
Elo 评级公式。

步骤 3: 利用 SWIM 解决成本问题

循环赛的缺点是成本。比较 \(N\) 个模型需要 \(O(N^2)\) 次比较。如果你有 100 个模型，那是极其昂贵的。

为了解决这个问题，作者提出了瑞士制迭代匹配 (Swiss-Wise Iterative Matchmaking, SWIM) 。

受瑞士制锦标赛 (常见于国际象棋或万智牌) 的启发，SWIM 的工作原理如下:

  1. 给每个模型初始化一个粗略的分数。
  2. 将模型与当前分数相近的对手进行匹配。
  3. 根据结果更新分数。
  4. 重复上述步骤。

因为模型只与它们水平相近的对手战斗，系统收敛到正确排名的速度要快得多——大约是 \(O(N \log N)\) 的复杂度。这使得对大量模型进行排名成为可能，而不会破产。

5. 实验结果: 它有效吗？

自动化裁判的终极测试是它与人类的一致程度。研究人员将他们的新排名方法与 Chatbot Arena 进行了比较，后者是一个成千上万人类对模型输出进行投票的众包平台。

与人类判断的相关性

结果是决定性的。循环赛方法 (结合 Bradley-Terry 模型) 显著优于标准的 AlpacaEval 胜率。

相关性表格。 图 5: 与标准的 AlpacaEval 2.0 相比，转向循环赛 + Bradley-Terry 模型使与人类排名的一致性 (斯皮尔曼相关系数) 提高了超过 13%。

SWIM vs. 循环赛

至关重要的是，作者表明高效的 SWIM 算法实现了与昂贵的循环赛方法几乎相同的准确性。

比较 SWIM 和循环赛性能的图表。 图 6: 绿线 (SWIM) 几乎完美地跟随蓝线 (循环赛)，始终击败标准的 AlpacaEval (红线)。

这证实了我们可以在不进行详尽的每对比较的计算成本下，获得高质量、考虑到传递性的排名。

6. 结论和要点

“LLM-as-a-Judge”的广泛采用是 AI 发展的一个主要解锁，但这篇论文作为一个重要的现实检验 (Sanity Check) 至关重要。我们不能盲目地相信 AI 裁判是合乎逻辑的。

给学生和从业者的关键要点:

  1. 传递性是一个迷思: 不要假设因为模型 A > B 且 B > C，所以 A > C。LLM 的偏好是充满噪音且循环的。
  2. 基线是危险的: 基于单一固定基线 (如 GPT-4 Preview) 的排名是不稳定的。改变基线会改变排行榜。
  3. 数学来救援: 像 Bradley-Terry 模型这样的统计方法对于将充满噪音的成对数据转换为稳健的排名至关重要。
  4. 效率很重要: 你不需要模拟每一场比赛。像 SWIM 这样的智能匹配算法允许以一小部分的计算成本进行准确排名。

随着我们迈向更自主的 AI 智能体，准确评估它们成为一个安全问题。通过承认并缓解非传递性，我们在迈向我们可以真正信任的评估框架的道路上又近了一步。

本文讨论的图片和数据基于论文《Investigating Non-Transitivity in LLM-as-a-Judge》(2025)。