引言

像 LLaMA 和 GPT 这样的大型语言模型 (LLMs) 已经彻底改变了自然语言处理领域，但它们伴随着巨大的代价: 体积庞大。拥有数十亿个参数使得在标准硬件上部署这些模型成为一场后勤噩梦，主要是由于高内存占用和计算延迟。这引发了网络稀疏化 (Network Sparsity) 研究的热潮——这类技术旨在从模型中移除“不重要”的参数 (权重) ，使其更小、更快，同时不牺牲智能水平。

流行的训练后稀疏化方法，如 SparseGPT 和 Wanda，已经取得了很大进展。它们允许我们在不进行昂贵重训练的情况下“一次性 (one shot) ”修剪已训练好的模型。然而，这里有一个问题。大多数此类方法在整个网络中应用统一稀疏率 (uniform sparsity rate) 。 如果你想要一个 50% 稀疏的模型，它们会从每一层移除 50% 的权重。

但是，所有层都是生而平等的吗？直觉告诉我们要否定。有些层负责基础特征提取，而其他层则负责细化高级概念。

在这篇深度文章中，我们将探讨一篇题为 《Determining Layer-wise Sparsity for Large Language Models Through a Theoretical Perspective》 (通过理论视角确定大型语言模型的层级稀疏度) 的精彩论文。研究人员发现了一个被称为 “重构误差爆炸 (Reconstruction Error Explosion) ” 的关键现象——即早期层的误差在通过网络传播时会像滚雪球一样越滚越大。他们的解决方案被恰当地命名为 ATP (A Theoretical Perspective，理论视角) , 摒弃了复杂的启发式方法和昂贵的搜索算法。取而代之的是，他们推导出了一个基于数学基础的、优雅的解决方案: 一个单调递增的等差数列。

简单来说: 保持早期层稠密，而在后期层进行激进的剪枝。让我们探讨一下为什么这个简单的规则如此有效。

问题所在: 重构误差爆炸

要理解为什么标准剪枝会失败，我们首先需要理解重构误差 (Reconstruction Error) 。 当我们修剪一层 (将某些权重设为零) 时，该层的输出与原始稠密层的输出相比会发生微小的变化。这种差异就是重构误差。

任何剪枝算法的目标都是最小化这个误差。然而，现有方法通常孤立地对待各层，或者假设统一的剪枝比例是“足够安全”的。研究人员发现，这种假设忽略了深度神经网络的累积性质。

滚雪球效应

作者提出了一个理论框架，揭示了一种连锁反应。

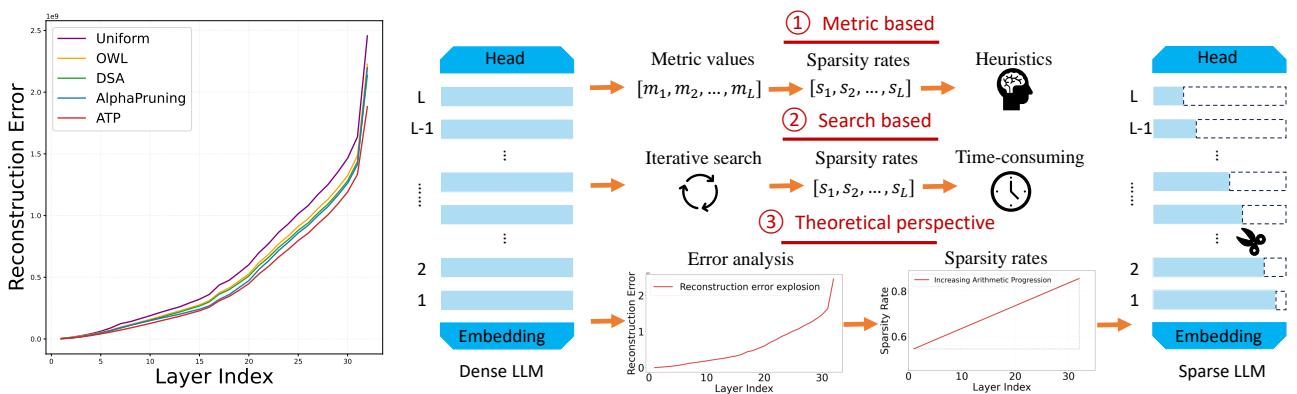
图 1: (左图) 展示了不同层级稀疏化方法之间的重构误差比较。所有方法都面临“重构误差爆炸”的问题；然而，与其他方法相比，我们的方法实现了更低的重构误差。 (右图) 展示了我们的方法与其他层级稀疏化方法的比较。

如图 1 (左) 所示，观察“Uniform” (紫色) 线条。重构误差在早期层 (索引 0-10) 很低，但随着网络深度的增加 (索引 20-30) ，误差急剧上升。这就是重构误差爆炸 。

该图还将 ATP 方法与其他方法进行了对比:

  1. 基于度量 (启发式) : 使用手工制定的规则 (如 OWL 中的离群值比例) 来猜测层的重要性。
  2. 基于搜索: 使用进化算法 (如 DSA) 寻找最佳比例，这需要大量的计算时间。
  3. ATP (理论视角) : 使用推导出的数学规则 (即按等差数列进行剪切) 。

爆炸现象的理论证明

论文通过两个关键定理将这种“爆炸”形式化。

定理 3.1: 稀疏度增加导致局部误差增加 首先，作者证明了增加特定层的稀疏度总是会增加该层的重构误差。如果你移除更多的权重，近似效果就会变差。

低稀疏度版本与高稀疏度版本之间的误差差异量化如下:

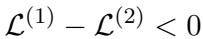
展示两个稀疏度水平之间重构误差差异的公式。 展示重构误差差异为负的公式，意味着较低的稀疏度产生较低的误差。

通俗地说: 剪得越多，坏得越多。

定理 3.2: 累积效应 这是关键的洞见。误差不仅仅停留在它发生的层。第 \(i\) 层的输出变成了第 \(i+1\) 层的输入。如果输入带有噪声 (由于第 \(i\) 层的剪枝) ，第 \(i+1\) 层将更难重构其原始输出，即使第 \(i+1\) 层本身是完美的。

作者将第 \(i\) 层的重构误差定义为:

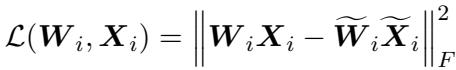
将重构误差定义为稠密输出与稀疏输出之差的 Frobenius 范数的公式。

然后他们证明了下一层的误差受到上一层误差的限制:

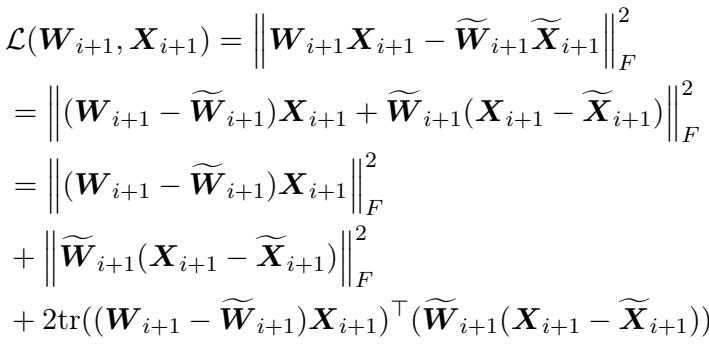
基于第 i 层推导第 i+1 层重构误差的公式。

简化这种关系后，他们得出了一个强有力的不等式:

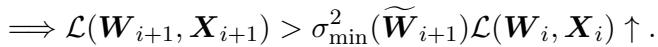
展示第 i+1 层的误差严格大于第 i 层误差的一个倍数的公式。

这个不等式告诉我们, 误差会传播并放大 。 如果你破坏了 LLM 的第一层，你不仅仅是伤害了第 1 层；你还提高了第 2 层、第 3 层等后续层的“误差底线”。当信号到达第 32 层时，累积的误差已经爆炸，破坏了模型连贯推理的能力。

这一理论分析指向了一个清晰的策略: 我们必须优先保证早期层的准确性。

解决方案: ATP (理论视角)

如果早期层因为误差传播最远而最危险，而后期层因为误差传播“距离”较短而相对安全，那么合乎逻辑的结论就是采用单调递增的稀疏率 。

我们应该对早期层进行很少的剪枝 (或者不剪) ，随着深度的增加提高剪枝率。

等差数列

虽然我们可以尝试学习一条复杂的增长曲线，但作者建议使用最简单的增长函数: 等差数列 (Arithmetic Progression) 。

他们使用以下公式定义第 \(i\) 层的稀疏率 \(s_i\):

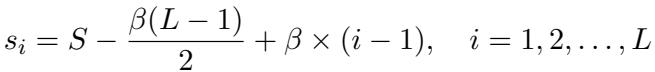
使用等差数列计算层级稀疏度的公式。

各变量代表的含义如下:

  • \(s_i\) : 第 \(i\) 层的稀疏率。
  • \(S\) : 整个模型的目标平均稀疏率 (例如 70%) 。
  • \(L\) : 总层数。
  • \(\beta\) : 公差 (或斜率) 。这是我们需要找到的唯一超参数。

这个公式确保了所有层稀疏率的平均值正好等于 \(S\)，同时允许稀疏率向上倾斜。

为什么这比搜索更好？

像 DSA (发现稀疏分配) 这样的方法使用进化搜索来寻找稀疏率。这可能需要数天的 GPU 时间和数千次迭代。

相比之下，ATP 方法只需要找到最佳的 \(\beta\)。由于稀疏率必须在 0 到 1 之间，\(\beta\) 的有效范围极其狭窄。

对于目标稀疏度为 70% 的 LLaMA-7B 模型，\(\beta\) 的有效范围大约是 \(0 < \beta \leq 0.019\)。

  • 如果 \(\beta\) 太高，第一层的稀疏度会降到 0 以下 (不可能) ，或者最后一层会超过 1。
  • 作者使用了步长为 0.002 的简单网格搜索 (Grid Search) 。
  • 这意味着他们只需要检查大约 9 个值 。

ATP 不需要在数天内进行搜索，而是在标准 GPU 上大约 18 分钟内就能找到最佳分配。

可视化分配

这种等差数列与其他方法相比如何？

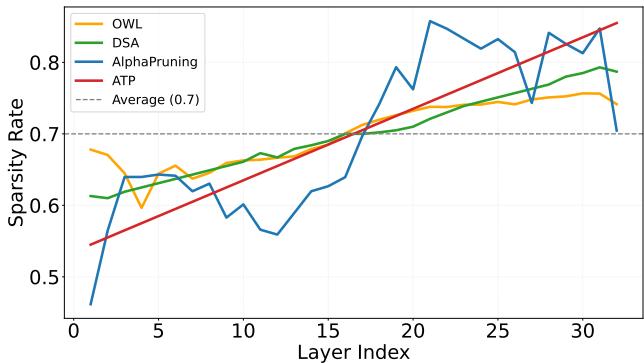
图 3: 与其他方法的层级稀疏率分布比较。

在上面的图 3 中, 红线 (ATP) 的起始点比所有其他方法都低 (大约 40% 的稀疏度) ，并在最后一层线性增加到超过 90%。

  • DSA (绿色) 和 OWL (橙色) 波动剧烈。它们可能会激进地修剪中间某一层，然后放过下一层。
  • AlphaPruning (蓝色) 保持比率平坦，然后在末端激增。
  • Uniform (虚线) 是朴素的直线。

ATP 的线条平滑且一致。通过从较低处开始，它保留了关键的早期特征提取，防止了我们之前看到的“误差爆炸”。

理论最优性

等差数列只是运气的猜测吗？作者提供了一个定理 (定理 3.5) ，证明了单调递增方案严格优于非单调方案。

他们通过证明以下一点得出了这个结论: 如果你有一对层，其中较早层的稀疏度高于较晚层 (违反了单调性) ，你可以交换它们的稀疏率，从而严格减少总重构误差。

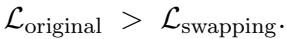
展示原始误差大于交换为单调顺序后误差的公式。

这意味着最优分布必须是稀疏度随着深度增加而增加的分布。等差数列是这种最优曲线的一个稳健近似。

实验与结果

理论听起来很可靠，但在实践中效果如何？作者在各种模型 (LLaMA, OPT, Vicuna) 和任务上测试了 ATP。

1. 零样本准确率 (Zero-Shot Accuracy)

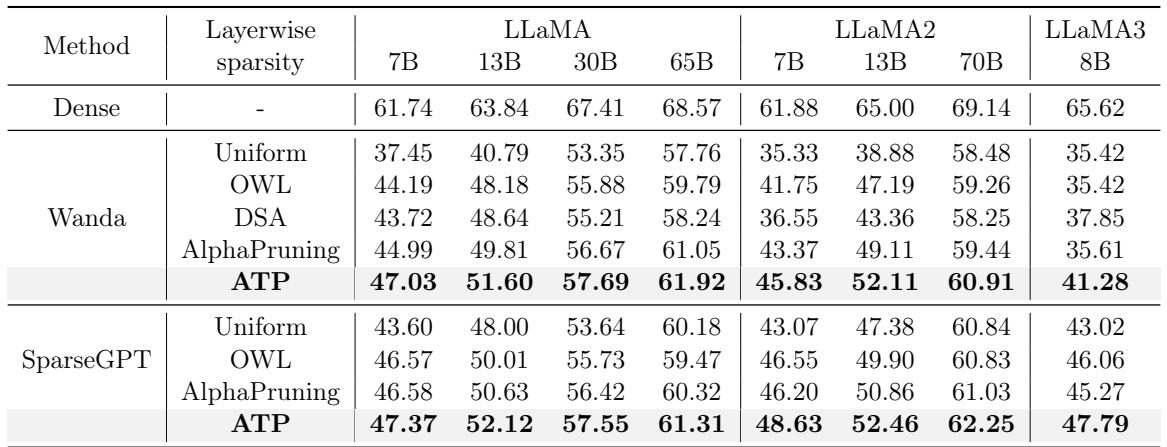
检验 LLM 能力最直接的方法是推理任务上的零样本性能。表 1 比较了 ATP 与 OWL、DSA 和 AlphaPruning 等最先进方法在 70% 稀疏度下的表现。

表 1: 使用各种稀疏化方法获得的 70% 稀疏 LLM 在 7 个任务上的平均零样本准确率比较。

关键要点:

  • 显著提升: 在 LLaMA-7B 上，ATP 将准确率从 37.45% (Wanda 基线) 提升到了 47.03% 。
  • 击败 SOTA: 它在几乎所有模型尺寸 (7B 到 70B) 上都优于复杂的 AlphaPruning 和 DSA 方法。
  • 持续胜出: 无论使用 Wanda 还是 SparseGPT 作为基础剪枝器，应用 ATP 的层级比率都能产生最佳结果。

2. 语言建模 (困惑度/Perplexity)

困惑度衡量模型对新文本的困惑程度 (越低越好) 。在主要稀疏区域，困惑度通常会飙升。

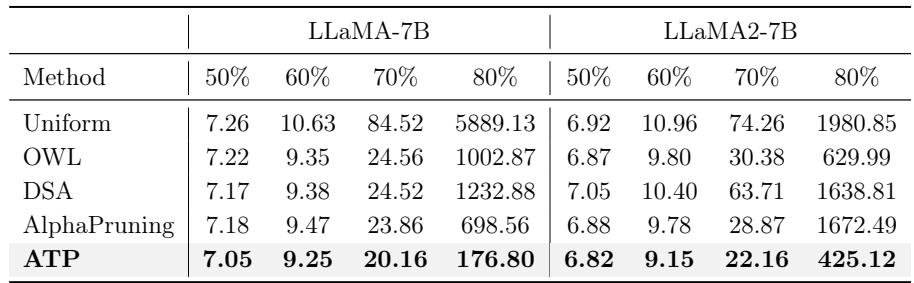
表 3: Wanda 获得的稀疏 LLaMA-7B/2-7B 在不同稀疏率下的 WikiText-2 困惑度。

看表 3，在 70% 稀疏度下的结果令人震惊:

  • Uniform (均匀) : 84.52 (模型已损坏) 。
  • OWL: 24.56。
  • ATP: 20.16 。

在 80% 稀疏度下，差异更加巨大的。均匀稀疏度爆炸至 5889，而 ATP 稳定在 176。这证实了保护早期层可以使模型承受更高的整体压缩率。

3. 与昂贵的搜索相比

有人可能会争辩说，复杂的贝叶斯搜索 (探索数千种组合) 会找到比简单的等差直线更好的解决方案。

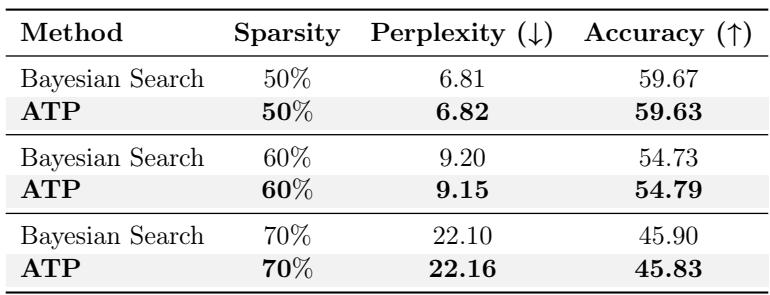
表 5: ATP 与贝叶斯搜索的比较。

表 5 揭示了一个令人惊讶的结果。 ATP 匹敌贝叶斯搜索。

  • 在 70% 稀疏度下，贝叶斯搜索达到了 22.10 的困惑度。
  • ATP 达到了 22.16。
  • 差异在于: 贝叶斯搜索耗时 33 小时 。 ATP 耗时 18 分钟 。

这表明最佳稀疏度的“搜索空间”实际上非常简单: 它只需要是一个向上的斜坡。

4. 实际加速

剪枝的最终目标是速度。非均匀稀疏度会损害推理速度吗？ (例如，如果某一层很稠密，它会成为瓶颈吗？) 。

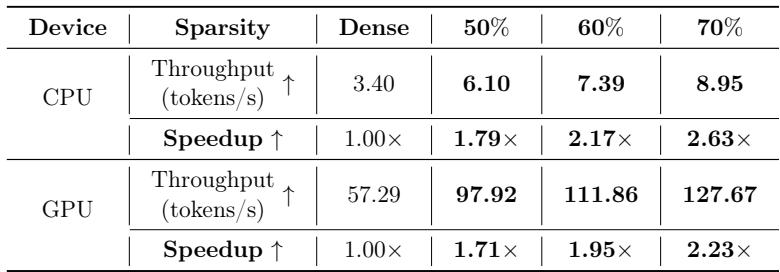
表 6: 稀疏 LLaMA2-7B 在 CPU 和 GPU 上的端到端推理加速。

表 6 显示 ATP 提供了巨大的加速。

  • 在 CPU 上，70% 稀疏的模型运行速度快了 2.63 倍 。
  • 在 GPU 上，运行速度快了 2.23 倍 。

因为参数总数减少了 70%，无论层级分布如何，计算负载都会显著下降。

寻找最佳点: Beta 参数

我们之前提到找到 \(\beta\) (斜率) 很快。但是 \(\beta\) 的选择重要吗？

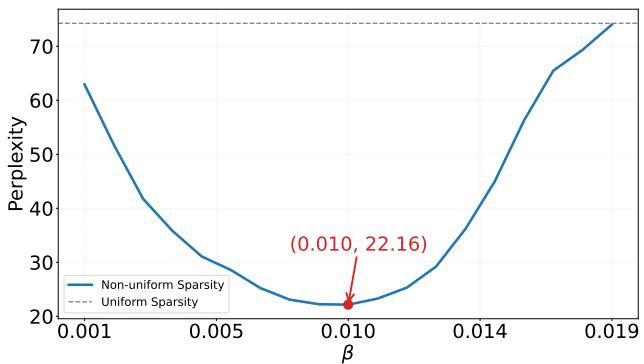
图 4: 不同 beta 设置对 70% 稀疏 LLaMA2-7B 困惑度的影响。

图 4 显示了 \(\beta\) 与困惑度之间的关系。它形成了一个完美的凸“U”形。

  • 如果 \(\beta\) 为 0，我们得到均匀稀疏度 (高困惑度) 。
  • 随着 \(\beta\) 增加，我们使稀疏度倾斜更多 (保护早期层) ，困惑度下降。
  • 如果 \(\beta\) 太高，我们对最后几层的修剪过于激进 (接近 100%) ，困惑度再次上升。

这种清晰的凸性解释了为什么网格搜索如此有效——有一个清晰的全局最小值可供查找。

结论

论文《Determining Layer-wise Sparsity for Large Language Models Through a Theoretical Perspective》为 AI 研究提供了一个令人耳目一新的教训: 有时，理论胜过暴力求解。

通过识别性能下降的根本原因——重构误差爆炸——作者推导出了一个比现有启发式方法更简单、更快速、更有效的解决方案。 ATP 方法教会我们，在深度网络中，早期层是基础。如果你破坏了地基，整栋楼都会倒塌。通过小心对待这些层，并仅在顶部进行激进的剪枝，我们可以将巨大的 LLM 压缩成高效、可用的模型，而不会失去它们的智能。

对于学生和从业者来说，这种方法很容易实现。它只需要添加几行代码来生成等差数列掩码，就能在稀疏模型上获得两位数的准确率百分比增益。这是一个令人信服的提醒: 理解模型为什么失败，往往比简单地搜索让它工作的参数更有价值。