引言: 学习的艺术

想象一下你正在学习弹吉他。你从扫几个基本的和弦开始——G、C 和 D。一周后，你已经掌握了它们。现在，如果你想成为一名演奏大师，你应该怎么做？你应该在接下来的一年里一遍又一遍地弹奏这三个和弦吗？还是应该刻意寻找高难度的指法、复杂的爵士音阶，以及那些强迫你的手指以不舒服的方式伸展的乐曲？

对任何人类来说，答案显而易见: 刻意练习 。 进步不是通过被动地重复已知的事物取得的，而是通过持续接触那些处于你能力极限边缘的任务来获得的。

然而，在人工智能的世界里，我们经常忘记这一原则。当我们训练深度学习模型时——特别是使用其他 AI 模型生成的合成数据时——我们倾向于预先生成一个巨大的、静态的数据集。我们将这些数据喂给学生模型，希望它能学会。但就像那个只会弹那几个和弦的吉他手一样，模型很快就会遇到收益递减点。增加更多“简单”的数据不再能提升性能。

在这篇文章中，我们将深入探讨一篇引人入胜的论文，题为 《Improving the Scaling Laws of Synthetic Data with Deliberate Practice》 (通过刻意练习改善合成数据的扩展定律) 。 研究人员提出了一个动态框架，其中生成模型 (老师) 和分类器 (学生) 在一个连续的循环中进行交互。老师不再生成随机数据，而是生成学生当前觉得困惑的特定样本。

这一理念上的简单转变带来了巨大的效率提升: 与传统方法相比，仅需 3.4 倍到 8 倍更少的数据即可达到更好的准确率。

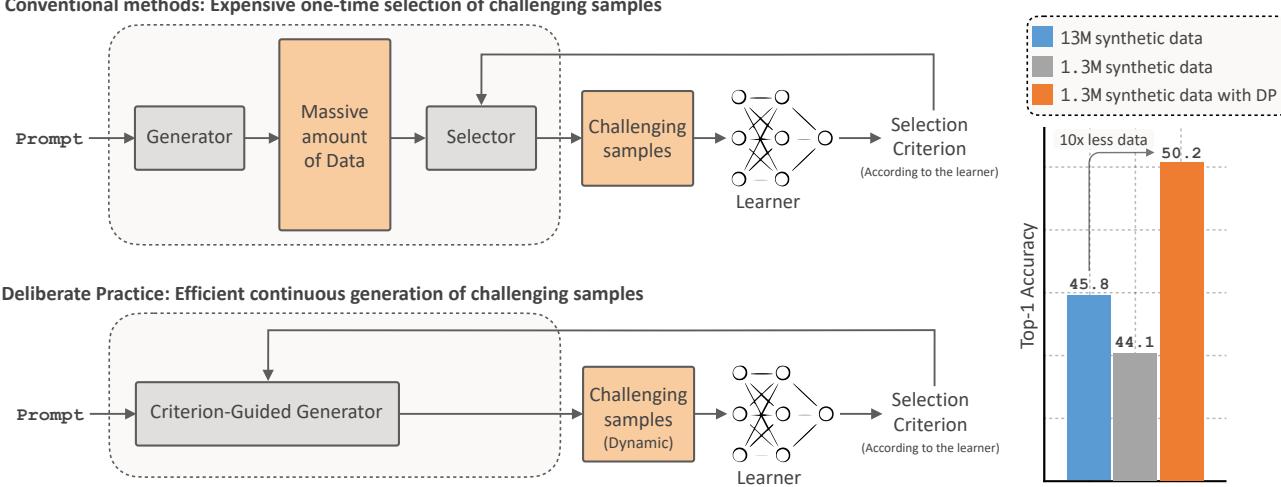
刻意练习与传统方法的概念对比。传统方法生成海量静态数据池并进行剪枝。刻意练习通过反馈循环直接生成具有挑战性的样本。

问题: 合成数据的瓶颈期

我们要生活在一个真实世界标注数据正在成为瓶颈的时代。收集数据昂贵、引发隐私问题，而且数量有限。自然地，研究人员转向了 文本生成图像 (T2I) 生成模型 (如 Stable Diffusion) 来创建无限的合成数据集。

理论很诱人: 如果我们有一个能生成任何图像的模型，难道我们不能仅通过合成数据来训练一个能识别任何事物的分类器吗？

然而，实证研究揭示了一个残酷的现实: 合成数据的扩展遵循 收益递减的幂律分布 。 你可以将数据集大小翻倍，但准确率的增益会迅速缩水。这是因为生成模型默认倾向于生成“原型”样本——即标准的、易于识别的图像 (例如，一只坐在草坪上的金毛寻回犬) 。一旦分类器学会了标准金毛寻回犬的样子，再看一百万张同样的照片也提供不了什么教育价值。

“先生成后剪枝”的低效性

为了解决这个问题，之前的工作尝试使用 剪枝 。 其工作流程如下:

  1. 生成海量的随机合成图像池 (例如，1000 万张图像) 。
  2. 使用某种指标 (如预测熵) 来识别“困难”或信息量大的图像。
  3. 扔掉 90% 的数据，只用剩下的前 10% 进行训练。

虽然这比随机训练效果好，但在计算上非常浪费。你花费了大量 GPU 算力生成数百万张图像，结果只是为了删除它们。

这篇论文提出了一个根本性的问题: 与其生成垃圾数据然后扔掉，我们能不能从数学上强制生成器在一开始就只生成“困难”的样本?

解决方案: 刻意练习 (DP)

研究人员引入了一个名为 刻意练习 (DP) 的框架。它将训练流程从直线变成了动态循环。

该过程基于一种 耐心机制 运作:

  1. 初始训练: 从一个小的、随机的合成数据集开始。训练分类器直到其验证准确率进入平台期 (停止学习) 。
  2. 反馈: 一旦学习者停滞不前，利用其当前状态来计算 熵 (不确定性) 。
  3. 针对性生成: 利用这个熵来引导扩散模型。强迫它生成能最大化学习者困惑度的新图像。
  4. 循环: 将这些新的、困难的样本添加到数据集中并恢复训练。重复此过程。

这反映了人类的学习过程。你练习直到遇到瓶颈，找出弱点，针对该弱点练习，然后进步。

数学原理: 熵引导采样

我们如何告诉扩散模型“生成一些令人困惑的东西”？我们需要修改生成过程的数学公式。

标准的扩散模型通过求解逆向随机微分方程 (SDE) 来生成数据。我们通常从分布 \(P\) 中采样。然而，我们希望从目标分布 \(Q\) 中采样，该分布强调信息量大的样本。

标准分布 P 与信息分布 Q 之间的关系。

这里，\(\pi\) 是一个优先考虑信息样本的加权函数。

在标准扩散过程中，逆向 SDE 如下所示:

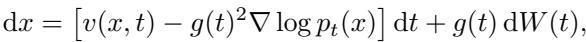
标准逆向 SDE 方程。

为了从信息分布 \(Q\) 而不是 \(P\) 中采样，我们应用 吉尔萨诺夫定理 (Girsanov’s Theorem) 。 该定理告诉我们，改变概率测度会在 SDE 的漂移项中引入一个“修正”项。

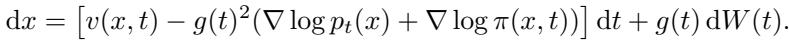
带有修正项的修正逆向 SDE。

注意这个新项: \(\nabla \log \pi(x, t)\)。这是我们加权函数的梯度。它就像一个方向盘，将生成过程推向潜空间中的高价值区域。

向导: 分类器熵

作者根据分类器 (\(f_\phi\)) 的 香农熵 (\(H\)) 定义了加权函数 \(\pi\)。高熵意味着分类器对图像的类别不确定 (例如，这是猫还是狗？) 。

熵加权函数。

为了高效地实现这一点，他们使用了去噪扩散隐式模型 (DDIM)。在图像生成过程中，在每个时间步 \(t\)，模型都有一个图像的噪声版本 \(x_t\)。作者近似出最终的干净图像 \(\hat{x}_{0,t}\) 并将其输入分类器以检查熵。

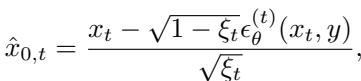
从噪声状态 x_t 近似干净图像 x_0。

然后，他们计算该熵相对于噪声图像的梯度，并将其添加到噪声预测 \(\epsilon_\theta\) 中。这引导了去噪过程。

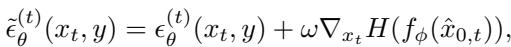
包含熵梯度项的修正噪声预测方程。

在这个方程中:

  • \(\epsilon_\theta^{(t)}\) 是标准的扩散噪声预测。
  • \(\omega\) 是一个超参数，控制我们强制“难度”的程度。
  • \(\nabla_{x_t} H\) 是增加分类器困惑度的方向。

通过设置 \(\omega > 0\)，生成器不再生成“平均”图像。它在积极尝试生成存在于当前分类器决策边界上的图像。

理论分析: 为什么“困难”数据扩展性更好

在看 ImageNet 的结果之前，理解这在数学上 为什么 有效至关重要。作者使用 随机矩阵理论 (RMT) 对合成数据的扩展定律进行了建模，提供了严谨的分析。

他们建立了一个简化的理论环境: 一个在高维数据上训练的线性分类器，在这里他们可以精确控制选择哪些数据点进行训练。

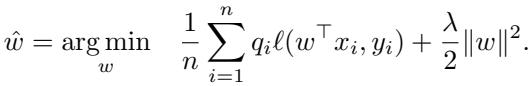
问题设置: 线性分类器训练。

他们将测试误差建模为数据集大小 (\(n\)) 和输入维度 (\(d\)) 的函数。具体来说，他们分析了 剪枝率 \(p\)——保留样本的概率。

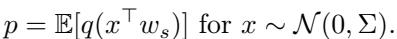
剪枝率 p 的定义。

选择策略 \(q(t)\) 决定了保留哪些样本。“保留困难样本 (Keep Hard)”策略只选择靠近决策边界的样本 (即 \(|t| \leq \xi\)) 。

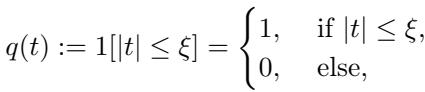
“保留困难样本”选择策略函数。

扩展定律的突破

利用这个理论框架，作者推导了不同选择策略下的渐近测试误差。这一理论的视觉结果令人震惊:

理论扩展行为。灰线 = 选择所有数据。红线 = 选择前 10% 最难的数据。

看上面的图表。

  • 黑/灰线 代表随机选择 (标准训练) 。曲线变得平缓；你需要指数级增加数据才能降低误差。
  • 红线 代表选择前 10% 最难的样本。它开始时的误差较高 (因为数据集很小) ，但随着数据的增加, 它超越了随机策略并且扩展速度快得多。

理论预测，在较小、较难的数据集上训练不仅仅是与在大型随机数据集上训练“一样好”——它从根本上改变了扩展指数。你从每比特数据中获得了更多的“智能”。

实验结果: 打破基准

作者在 ImageNet-100 和 ImageNet-1k 上验证了他们的框架，完全使用 Stable Diffusion (LDM-1.5) 生成的合成数据进行训练，并在真实世界的验证数据上进行测试。

1. 扩展性能

静态生成 (标准) 与刻意练习 (DP) 之间的对比非常鲜明。

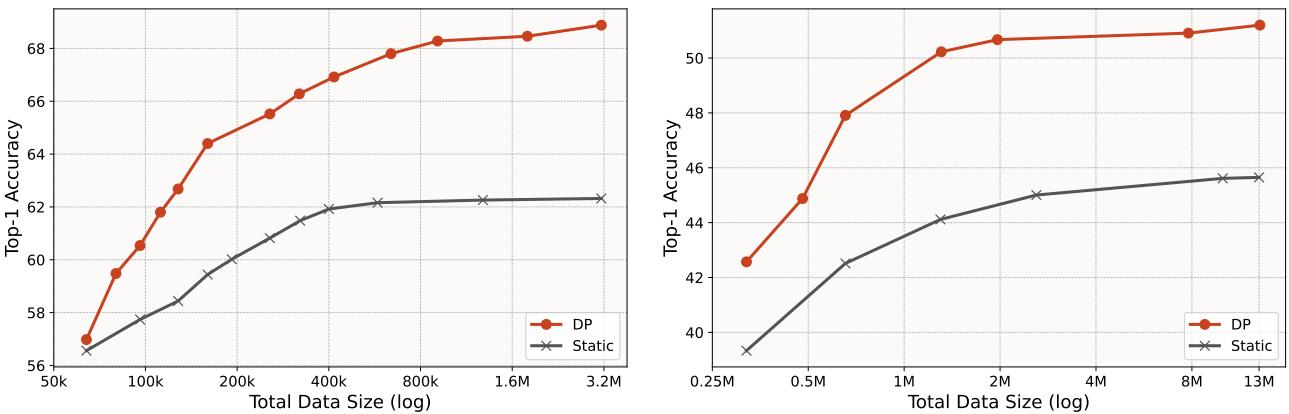
验证准确率 vs. 数据集大小。DP (蓝圈) vs 静态 (粉叉) 。

  • ImageNet-100 (左) : DP 使用 少 7.5 倍的数据 达到了与静态设置相同的准确率。
  • ImageNet-1k (右) : DP 使用仅约 64 万张图像就超过了最佳静态准确率 (在 1300 万张图像上训练) 。这相当于在性能相当的情况下 减少了 20 倍的数据量 。

2. 训练动态

最有趣的发现之一是训练指标的表现。通常，我们希望训练损失下降。但在刻意练习中，我们不断注入“困难”数据，这会导致损失飙升。

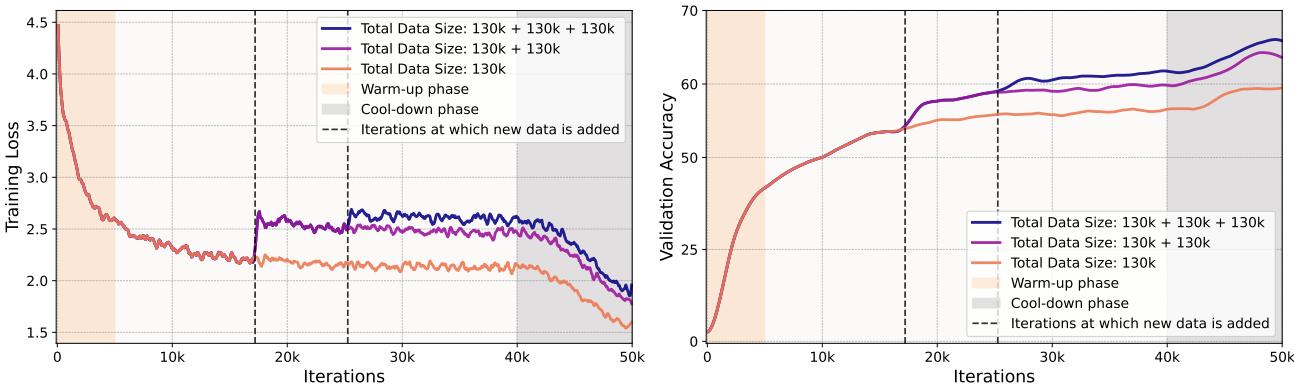
训练动态。左: 当添加新的困难数据时损失增加。右: 验证准确率跳升。

在上图中，垂直虚线代表分类器进入平台期、生成器注入一批新的熵优化数据的时刻。

  • 左图: 训练损失在虚线处 增加。这证实了新数据对模型来说确实很难。
  • 右图: 尽管训练损失较高, (真实数据上的) 验证准确率却跳升了 。 这就是有效学习的定义——与困难概念作斗争会带来更好的泛化能力。

3. 计算效率

对“困难样本挖掘”策略的一个主要批评是成本。如果你必须生成 100 张图像才能找到 1 张好的，这难道不是在浪费算力吗？

作者将 DP (直接生成) 与“显式剪枝” (生成很多，选择少量) 进行了比较。

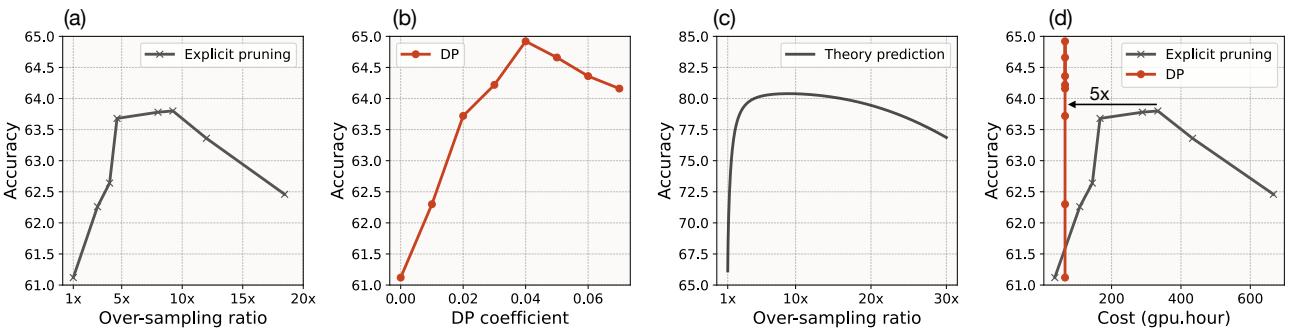
效率比较。图 (d) 显示准确率 vs GPU 小时数。

看上图中的 图 (d) 。

  • 与 显式剪枝 (蓝色) 相比, DP 方法 (橙色) 以显著更少的 GPU 小时数实现了高准确率。
  • 生成一张带有熵引导的图像比标准生成大约多花 1.8 倍的时间，但由于你需要生成的图像总数 少得多 , 整体计算成本 降低了 5 倍 。

工作流程的差异在此处得到了直观的展示:

高效采样 (DP) 与低效剪枝的比较。

可视化学习过程

一个“困难”样本看起来像什么？“难度”会随时间变化吗？

作者追踪了特定批次数据的错误率。他们发现，在第 10,000 次迭代时“困难”的样本，到了第 30,000 次迭代时变得“简单”了。这证实了静态数据集是次优的，因为“有信息量”的定义是一个移动的目标。

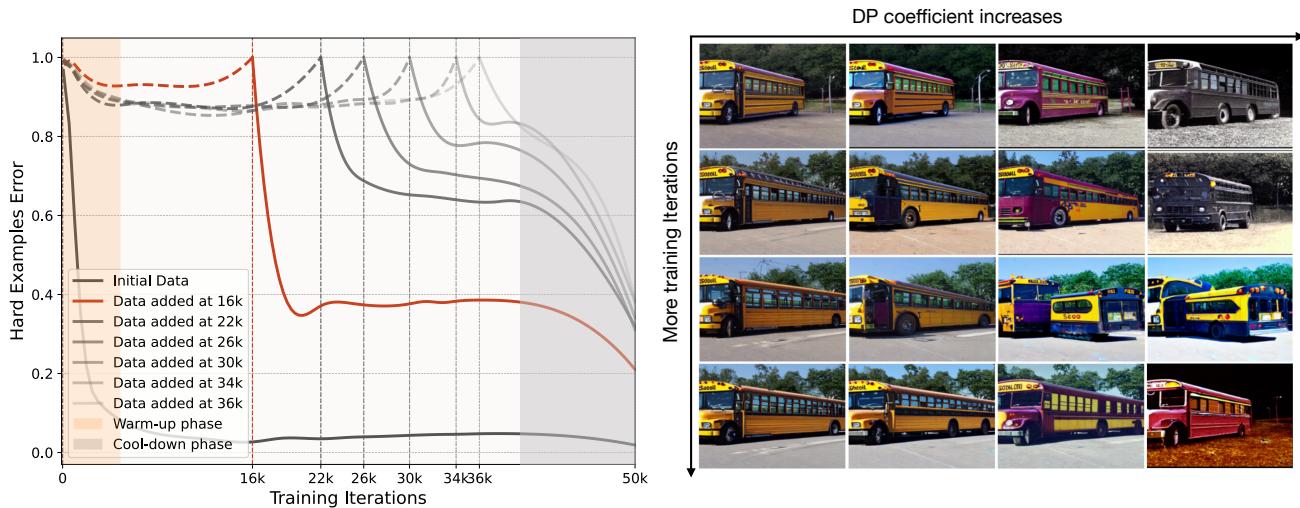
困难样本的错误轨迹。随着模型的学习，错误率下降。

我们还可以看到生成图像的演变。在训练的早期阶段，模型可能会被简单的颜色变化搞混。后来，它理解了颜色，但会被复杂的形状或视角搞混。生成器适应了这一点。

在下面“校车 (School Bus)”类别的例子中，早期的生成 (顶部) 可能集中在基本的黄色团块上。随着模型的学习，生成器 (在高熵引导 \(\omega\) 下) 开始产生奇怪的角度、扭曲的形状或不寻常的背景来挑战学习者。

‘校车’样本的演变。后期 (底部) 高引导 (右侧) 显示出更复杂的视角和形状。

同样，对于“狐狸 (Fox)”类别，初始数据 (顶部) 看起来有些单一。到了训练结束时 (底部) ，累积的数据集包含了各种各样的姿态、光照条件和背景。

‘狐狸’的初始训练数据与最终训练数据的比较。最终数据集更加多样化。

结论: 合成数据的未来

论文《Improving the Scaling Laws of Synthetic Data with Deliberate Practice》为我们如何处理 AI 训练提供了一个关键的转变。它让我们从“数据越多越好”的暴力思维，转向了一种更细致、更具教学意义的方法: “数据越好才越好”。

通过在学生 (分类器) 和老师 (生成器) 之间建立反馈循环，我们可以:

  1. 打破扩展平台期: 在随机采样达到饱和后继续提高准确率。
  2. 节省算力: 以大幅减少的数据集大小 (高达 8 倍) 和更少的训练迭代次数训练出更好的模型。
  3. 动态适应: 确保数据随模型能力的提升而演变。

表 1 总结了该方法相对于之前最先进的合成训练方法的优势:

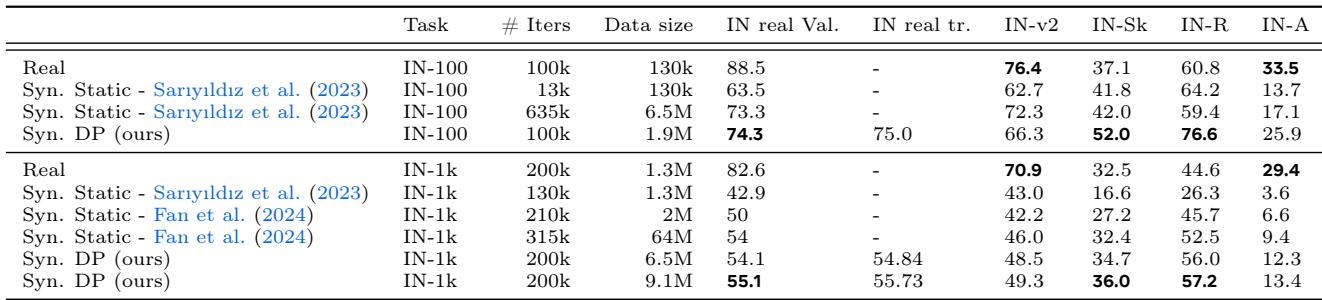
与之前工作的比较。DP (底部几行) 用更少的数据实现了更高的准确率。

这项研究表明，训练大型模型的未来可能不在于简单地抓取更多互联网数据，而在于合成高度针对性的、智能的课程，并根据模型实时调整。就像音乐老师指导学生练习越来越难的曲子一样，我们的生成模型可以引导我们的分类器走向鲁棒性和高性能。

这篇博客文章解释了 Askari-Hemmat 等人发表的研究成果《Improving the Scaling Laws of Synthetic Data with Deliberate Practice》(Meta FAIR, 2025).