两全其美：SPLIT 如何以贪婪算法的速度实现最优决策树

引言

在机器学习领域, 可解释性 (理解模型为什么做出预测) 与性能 (预测有多准确) 之间往往存在着痛苦的权衡。决策树是可解释性的典型代表。它们模仿人类的推理过程: “如果 X 为真，检查 Y；如果 Y 为假，预测 Z。”

然而，构建完美的决策树——即既高度准确又稀疏 (节点少) 的树——极其困难。这就引出了第二个权衡: 最优性 vs. 可扩展性 。

从历史上看，你只有两个选择:

1. 贪婪方法 (如 CART/C4.5) : 这些方法快如闪电。它们通过在每一步做出当下最好的决定来构建树。然而，这种方法往往比较短视，导致生成的树更大，准确性较低。
2. 最优方法 (如 GOSDT) : 这些方法使用动态规划等复杂技术来寻找数学上完美的树。它们稀疏且准确，但计算成本高昂，在复杂数据集上运行通常需要数小时甚至数天。

如果你不必二选一呢？

在论文 “Near-Optimal Decision Trees in a SPLIT Second” 中，研究人员引入了一族新算法——SPLIT、LicketySPLIT 和 RESPLIT——填补了这一空白。他们的方法生成的树实际上与最优树无法区分，但运行速度却快了好几个数量级。

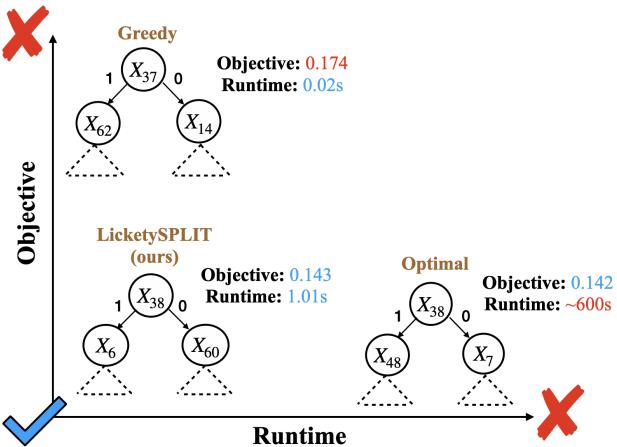
如图 1 所示，该算法达到了“完美平衡”，在实现最优方法的目标值的同时，保持了贪婪方法的运行速度。

背景: 为什么这很难？

要理解 SPLIT 的创新之处，我们首先需要了解传统决策树是如何构建的，以及为什么实现“最优”如此困难。

贪婪陷阱

标准的决策树算法是贪婪的 。 在根节点，它们查看所有可用的特征，并选择一个能最大化当前指标 (如信息增益) 的特征。

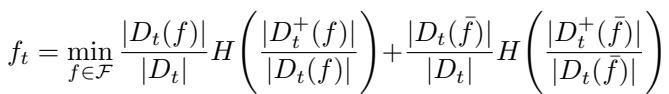
一旦做出分裂，算法就再也不会回头。它会对子节点重复这一过程。问题在于，现在看来“最好”的分裂可能会阻碍你在树的深层做出更好的分裂。这种短视往往导致树变得臃肿，难以解释且泛化能力差。

完美的代价

近年来, 最优稀疏决策树 (OSDT) 兴起。这些算法解决的是一个全局优化问题。它们试图最小化一个既惩罚分类错误又惩罚树的大小 (叶子数量) 的代价函数。

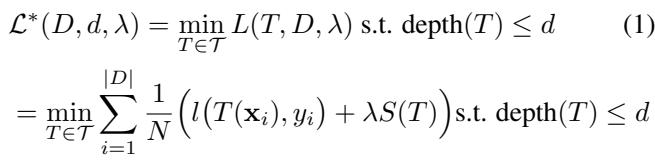
最小化这个方程 (方程 1) 是 NP 难问题。像 GOSDT 这样的算法使用分支定界 (BnB) 技术来搜索空间。它们虽然精妙，但从根本上受限于“维度灾难”。随着数据集增大或树变深，可能的树的数量呈指数级爆炸，使得大规模问题的最优搜索变得棘手。

罗生门集合 (The Rashomon Set)

论文还涉及了罗生门集合的概念。在复杂问题中，很少只有一个好模型。通常存在一组“足够好”的模型，它们的表现同样出色。

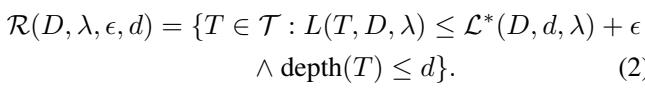
找到这个集合 (方程 2) 允许用户选择更符合领域知识或公平性约束的模型。然而，找到一个最优树已经很难了；找到所有好树更是难上加难。

核心洞察: 最优性在哪里最重要

研究人员做出了一个至关重要的观察，这成为了 SPLIT 的基础: 树中的并非所有决策都是生而平等的。

构建决策树时，靠近根节点 (顶部) 的分裂最为关键。它们划分整个数据集。这里的一个错误决策会波及整个结构。然而，随着你向叶子节点深入，子问题会变得更小 (数据点更少) 。

研究人员假设，虽然树的顶部需要强大的优化，但贪婪算法在靠近叶子节点的地方表现出奇地好。

他们通过分析罗生门集合中的最优树来验证这一点，并计算不同深度的分裂是“贪婪的” (即与简单 CART 算法的选择相同) 频率。

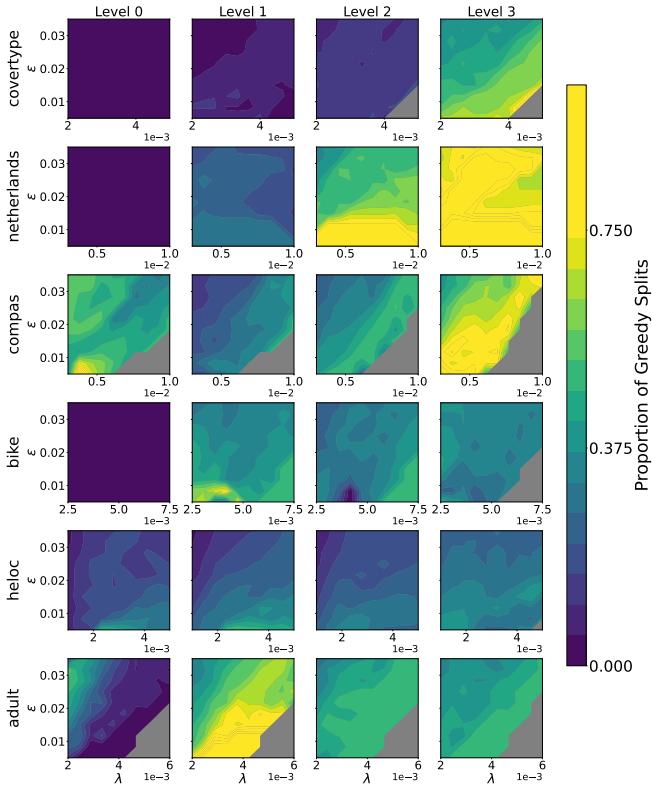
图 2 证实了这一直觉。在第 0 层 (根节点) ，分裂很少是贪婪的——这里需要优化。但当你接近第 3 层及更深处时，热图变成了黄绿色，表明最优树在底部经常默认采用贪婪选择。

这引出了 SPLIT 的指导原则: 在顶部执行繁重的最优搜索，而在底部切换到快速的贪婪搜索。

方法: SPLIT 和 LicketySPLIT

作者提出了一种“稀疏前瞻 (Sparse Lookahead)”策略。他们不再优化整个树 (太慢) 或完全不优化 (不准确) ，而是优化树的“前缀”直到一定深度。

1. SPLIT 算法

SPLIT 算法引入了一个名为前瞻深度 (\(d_l\)) 的参数。

• 对于树的顶部 \(d_l\) 层，算法使用完整的分支定界优化来探索所有分裂组合。
• 超过深度 \(d_l\) 后，算法通过运行快速的贪婪算法来估计分支的“代价”。

这使得算法可以“向前看”几步以避免纯贪婪搜索的陷阱，而无需付出探索深层树的整个指数空间的代价。

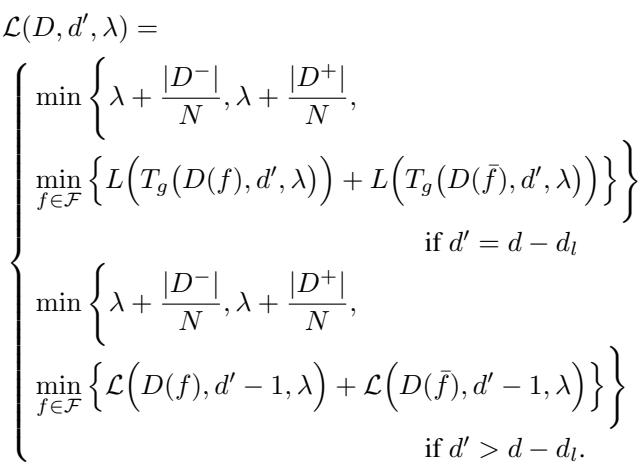
上图公式正式描述了这一点。如果剩余深度 \(d'\) 允许前瞻 (\(d' > d - d_l\)) ，它执行最优搜索 (底部情况) 。一旦达到前瞻限制，它就切换到贪婪近似 (中间情况) 。

2. LicketySPLIT: 多项式时间速度

虽然 SPLIT 很快，但作者引入了一个更快的变体: LicketySPLIT 。

LicketySPLIT 递归地应用前瞻概念。它本质上是以前瞻深度为 1 运行 SPLIT 来找到最佳根分裂，然后在左右子节点上递归调用自身。

因为它在每一步都分解问题，LicketySPLIT 在多项式时间 (\(O(nk^2d^2)\)) 内运行，而完全最优方法在指数时间内运行。这个理论保证是巨大的: 这意味着 LicketySPLIT 可以扩展到最优方法会崩溃或永远运行不完的数据集上。

3. RESPLIT: 快速罗生门集合

最后，他们将此逻辑应用于寻找罗生门集合 (所有好模型的集合) 。 RESPLIT 使用 SPLIT 方法找到一组有希望的“前缀”树，然后扩展它们。这使得在高维数据中探索“好模型云”变得可行。

实验与结果

理论主张很强，但在实践中效果如何？作者将 SPLIT 和 LicketySPLIT 与最先进的最优算法 (如 GOSDT 和 MurTree) 以及贪婪基线进行了比较。

1. 速度与精度的权衡

最令人信服的结果是运行时间的比较。

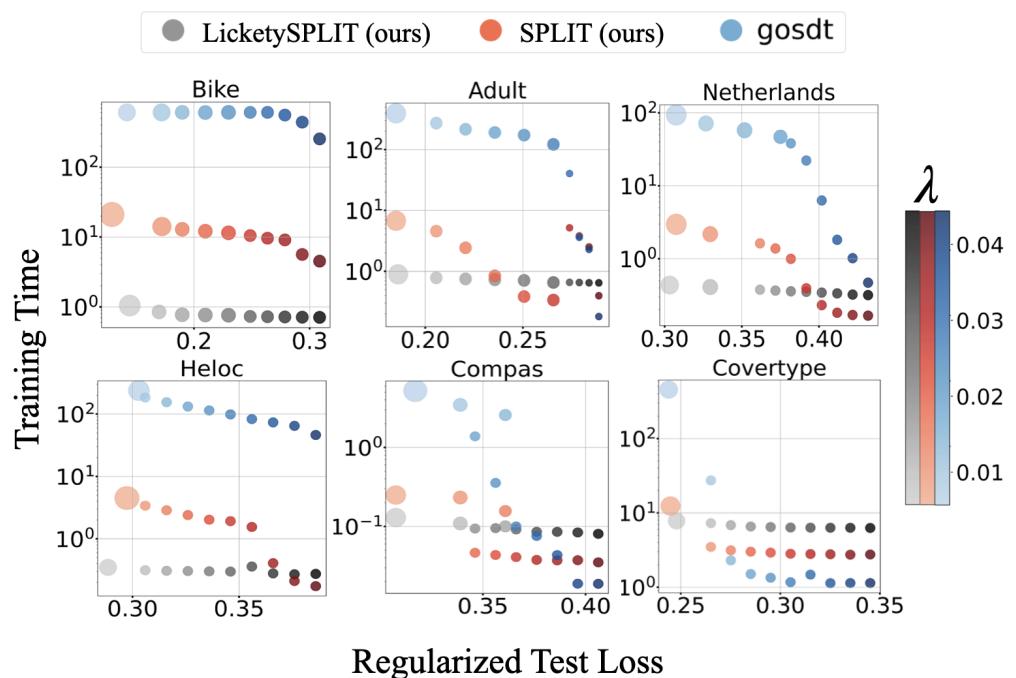
在图 3 中，我们看到了优化的“圣杯”。

• GOSDT (蓝点) : 实现了低损失，但位于最右侧 (慢，数百或数千秒) 。
• SPLIT/LicketySPLIT (红/灰圆圈) : 位于左下角。它们实现了与 GOSDT 相同的低损失 , 但时间仅为亚秒级或个位数秒。

在 Bike 数据集上，SPLIT 比最优基线快大约 100 倍 , 且性能损失可忽略不计。

2. 稀疏前沿

使用最优树的主要原因之一是保持树的小巧 (稀疏) 。SPLIT 生成的树会臃肿吗？

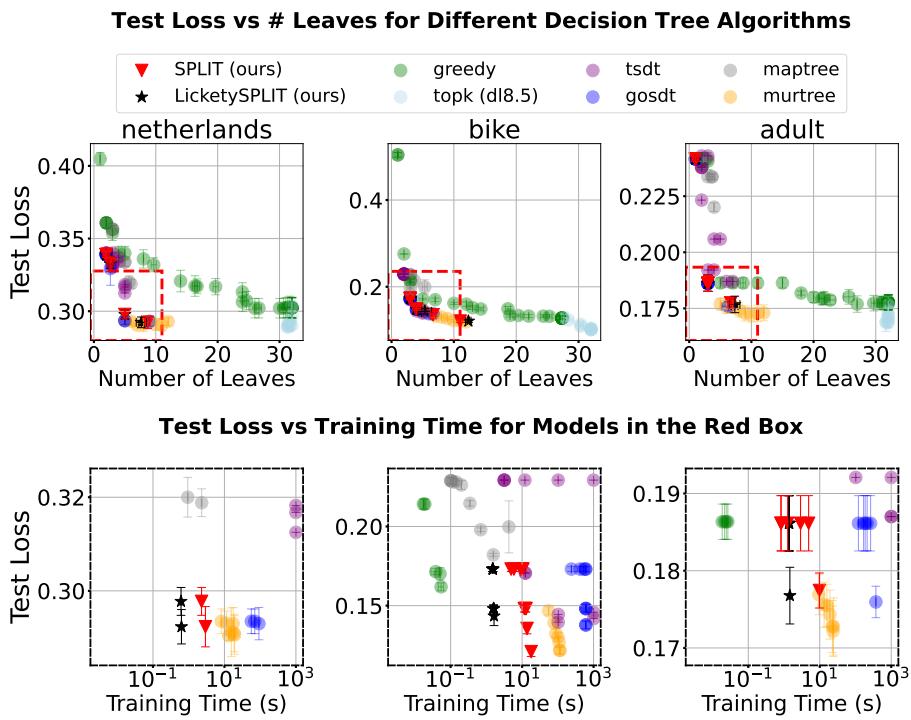
图 4 显示了测试损失 vs. 叶子数量的前沿。

• 贪婪树 (绿色) 通常是“高损失，多叶子” (图的右上角) 。
• SPLIT 和 LicketySPLIT (红/黑星号) 正好落在最优解 (蓝/黄) 之上。它们成功找到了位于理想“红框”内的稀疏、准确的模型。

3. 它们有多“最优”？

这些树是真的最优，还是仅仅接近？作者检查了 SPLIT 生成的树落在罗生门集合 (近最优模型集) 中的频率。

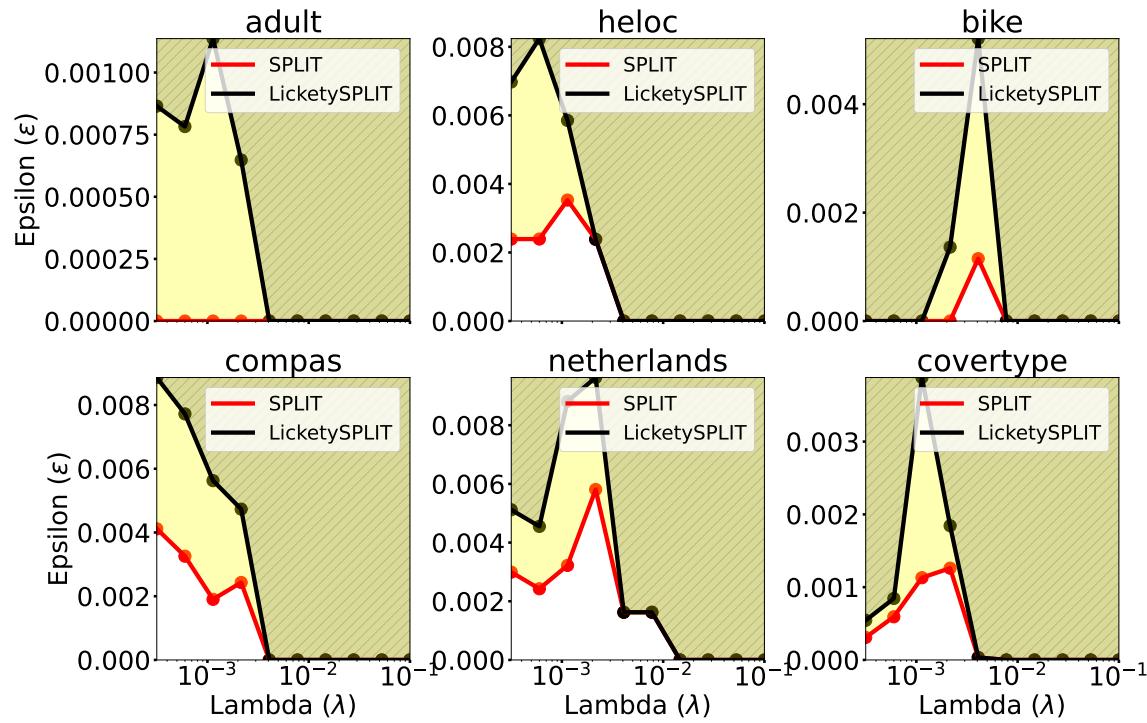
图 12 表明，即使在非常严格的约束下 (小 \(\epsilon\)) ，SPLIT 和 LicketySPLIT 生成的树本质上也是最优的。“最优性差距”——完美树与 SPLIT 树之间的差异——实际上不存在。

4. 前瞻深度分析

一个自然的问题是: “我们需要向前看多深？” 作者发现，大约 \(d/2\) (总深度的一半) 的前瞻深度在理论上是最小化运行时间的最佳选择。

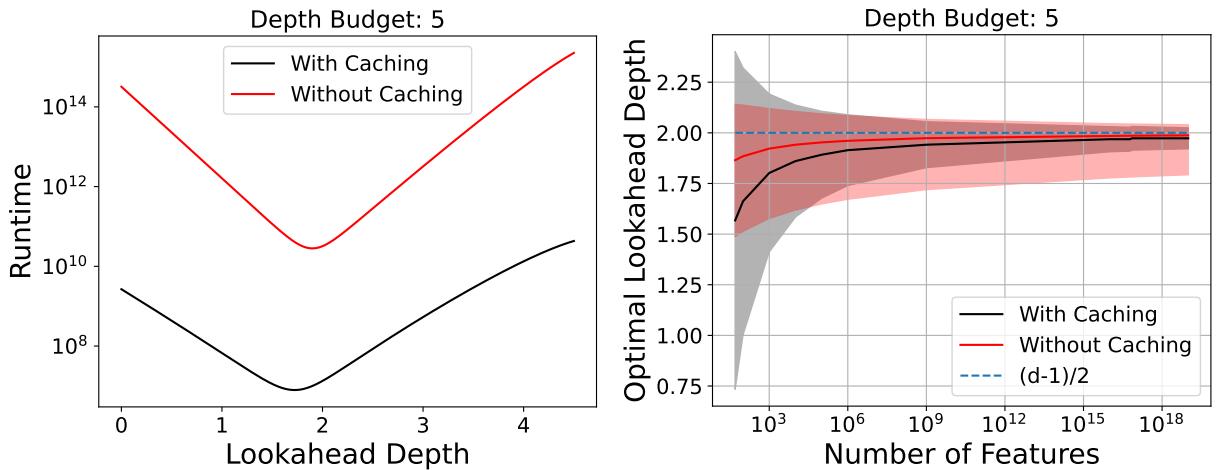
如图 19 所示，运行时间呈“U”形。

• 太浅: 你过于依赖贪婪算法，可能会做出糟糕的选择，需要更多的叶子来修正 (或者根本找不到好树) 。
• 太深: 你接近完全优化的指数成本。
• 最佳平衡点: 前瞻深度约为 2 (对于深度为 5 的树) 提供了最大的加速。

结论

论文 “Near-Optimal Decision Trees in a SPLIT Second” 挑战了“快”与“最优”之间的二元选择。

通过认识到深度优化在树的叶子附近收益递减，作者创造了一种混合方法。 SPLIT 和 LicketySPLIT 在关键时刻 (根部) 利用分支定界的力量，而在安全时刻 (叶部) 利用贪婪搜索的速度。

关键要点:

1. 效率: SPLIT 比当前最先进的最优求解器快好几个数量级。
2. 性能: 它几乎不牺牲任何准确性或稀疏性。
3. 可扩展性: LicketySPLIT 在多项式时间内运行，为在更大数据集上构建最优风格的决策树打开了大门。

这项工作表明，对于可解释的机器学习，我们不需要在任何地方都做到完美最优——我们只需要聪明地选择在哪里进行优化。