引言

在机器学习的世界里，对齐 (Alignment) 就是一切。无论你是在训练一个将噪声映射为图像的生成模型，还是对齐不同时间点的单细胞基因组数据，亦或是进行不同领域间的翻译，你本质上都在问同一个问题: 将质量从分布 A 移动到分布 B 的最佳方式是什么？

这就是 最优传输 (Optimal Transport, OT) 的核心问题。几十年来，OT 一直是比较和对齐概率分布的黄金标准，因为它尊重数据的潜在几何结构。它致力于寻找将一个数据集传输到另一个数据集的“最小代价”路径。

然而，一直存在一个巨大的陷阱: “计算高墙”。解决 OT 问题最流行的算法——Sinkhorn 算法 , 其复杂度呈二次方增长。如果你将数据量翻倍，计算时间和内存使用量将增加四倍。对于小数据集来说，这没问题。但在“大数据”时代——我们经常处理数百万个数据点——二次方复杂度根本行不通。它有效地将 OT 的强大功能锁在了一扇只有小数据集才能通过的大门之后。

研究人员尝试了各种变通方法: 使用小批量 (Mini-batches) 近似 (这引入了偏差) 或强制低秩约束 (这会损失分辨率) 。但是，如果你能两全其美呢？如果你能在数百万个点之间计算出高质量、全秩的对齐，且仅需线性内存和对数线性时间呢？

这正是论文 “Hierarchical Refinement: Optimal Transport to Infinity and Beyond” 所实现的突破。作者介绍了一种名为 HiRef 的新算法，该算法使用分而治之 (divide-and-conquer) 的策略，将最优传输扩展到了以前认为不可能的水平。在这篇文章中，我们将解构 HiRef 的工作原理，使其成为可能的数学洞见，以及这对数据对齐的未来意味着什么。

背景: 最优传输的瓶颈

要理解 HiRef 为何如此具有突破性，我们首先需要了解它所解决的问题。

Monge 和 Kantorovich 问题

最优传输可以追溯到 1781 年的 Gaspar Monge，他希望以最小的功将一堆土 (源分布 \(\mu\)) 移动去填满一个坑 (目标分布 \(\nu\)) 。在数学上，这被称为 Monge 问题 。 我们寻找一个映射 \(T\)，将 \(\mu\) 推向 \(\nu\)，同时最小化代价 \(c\):

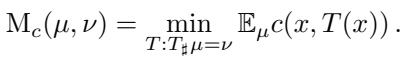
公式 1: Monge 问题表述。

这里，\(T(x)\) 是点 \(x\) 的目的地。Monge 问题的解是一个 确定性映射——一个将每个源点唯一配对到目标点的双射。

然而，Monge 映射并不总是存在 (例如，将一堆土分成两个坑) 。这引出了 Kantorovich 松弛 , 它允许质量拆分。我们不再寻找一个映射，而是寻找一个 耦合矩阵 (coupling matrix) \(\mathbf{P}\)。这个矩阵描述了多少质量从 \(x_i\) 移动到 \(y_j\)。

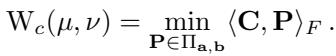
公式 2: 传输多胞形定义。 公式 3: Wasserstein 距离表述。

集合 \(\Pi_{\mathbf{a}, \mathbf{b}}\) 是所有有效耦合矩阵的集合，其中行之和为源分布 \(\mathbf{a}\)，列之和为目标分布 \(\mathbf{b}\)。最优解给出了 Wasserstein 距离，这是一个衡量分布差异的强大指标。

Sinkhorn 算法及其局限性

解决标准的 Kantorovich 问题在计算上非常昂贵 (立方时间，\(O(n^3)\)) 。随着 Sinkhorn 算法 (Cuturi, 2013) 的出现，情况有了突破，该算法增加了一个熵正则化项 \(H(\mathbf{P})\):

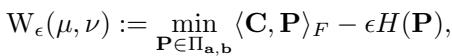
公式 4: 熵正则化 Wasserstein 表述。

这种正则化允许通过简单的矩阵缩放更新来更快地解决问题。然而，Sinkhorn 需要存储和操作 \(n \times n\) 的耦合矩阵 \(\mathbf{P}\)。

如果 \(n = 100,000\)，\(\mathbf{P}\) 有 \(100\) 亿个条目。 如果 \(n = 1,000,000\)，\(\mathbf{P}\) 有 \(1\) 万亿个条目。

这这就造成了二次方内存瓶颈 (\(O(n^2)\))。对于拥有数百万样本的现代数据集 (如 ImageNet 或单细胞转录组学) ，在标准硬件上通过 Sinkhorn 进行精确 OT 简直是不可能的。

低秩最优传输

为了绕过内存问题，研究人员开发了 低秩 OT (Low-Rank OT) 。 他们不再存储完整的 \(n \times n\) 矩阵 \(\mathbf{P}\)，而是将其近似为秩为 \(r\) (其中 \(r \ll n\)) 的较小矩阵的乘积。

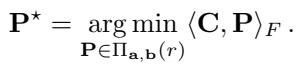
公式 5: 低秩 OT 问题。

使用 Scetbon 等人 (2021) 提出的分解方法，耦合表示为:

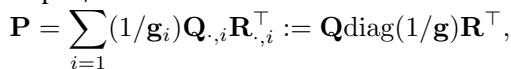
公式 6: 耦合矩阵 P 的分解。

这里，\(\mathbf{Q}\) 和 \(\mathbf{R}\) 将数据连接到 \(r\) 个“潜在”分量。这将复杂度从 \(O(n^2)\) 降低到 \(O(nr)\)，即与 \(n\) 呈线性关系。

权衡: 虽然低秩 OT 快速高效，但它本质上是“模糊的”。通过强制传输计划通过一个小秩 \(r\)，你失去了 Monge 映射那样的细粒度、一对一的对应关系。它有效地将数据点分组，但无法告诉你具体的点 \(x_i\) 映射到了哪个具体的点 \(y_j\)。

我们面临一个两难境地: Sinkhorn 提供高分辨率但无法扩展。 低秩 OT 可以扩展但会损失分辨率。

核心方法: 分层细化 (HiRef)

HiRef 的作者提出了一种巧妙的方法来弥补这一差距。他们的方法假设，如果我们递归地“放大”，我们可以利用低秩 OT 来构建高分辨率的 Monge 映射。

关键洞见: 共聚类 (Co-Clustering)

HiRef 背后的基本思想依赖于低秩 OT 的一个特定属性。当你解决一个低秩问题时，因子 \(\mathbf{Q}\) 和 \(\mathbf{R}\) 不仅仅是压缩数据；它们实际上是在对数据进行 聚类 。

具体来说，作者证明了一个理论结果 (命题 3.1) ，指出最优低秩耦合的因子有效地对点进行了“共聚类”。如果源数据集中的点 \(x\) 在最优 Monge 映射下映射到目标数据集中的点 \(y\)，那么低秩解很可能会将 \(x\) 和 \(y\) 分配到同一个潜在分量 (或簇) 中。

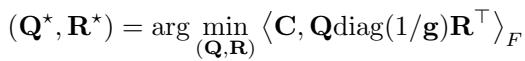
公式 8: 证明中使用的低秩优化问题。

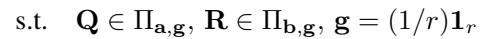
公式 9: 低秩优化的约束条件。

这一观察是“秘诀”所在。这意味着我们不仅可以将低秩 OT 用作一种近似，还可以将其用作一种 排序机制 。 它告诉我们: “数据集 X 中的所有这些点属于数据集 Y 中的所有那些点。我们还不知道确切的配对，但我们知道它们在同一个桶里。”

算法: 分而治之

HiRef 利用这一洞见来执行递归的多尺度细化。

第一步: 初始化 我们从两个完整的数据集 \(X\) 和 \(Y\) 开始。我们将此视为最粗糙的尺度。

第二步: 低秩分区 我们在当前集合之间解决一个低秩 OT 问题。使用得到的因子 \(\mathbf{Q}\) 和 \(\mathbf{R}\)，我们将 \(X\) 和 \(Y\) 划分为 \(r\) 个组 (共聚类) 。

因子 \(\mathbf{Q}\) 和 \(\mathbf{R}\) 充当分配矩阵。如果 \(\mathbf{Q}\) 的第 \(i\) 行在第 \(z\) 列具有最大值，则点 \(x_i\) 被分配给簇 \(z\)。我们对 \(Y\) 使用 \(\mathbf{R}\) 做同样的操作。这创建了配对的子集: \((X_1, Y_1), (X_2, Y_2), \dots, (X_r, Y_r)\)。

第三步: 递归细化 我们实际上是在放大。我们取子集对 \((X_1, Y_1)\) 并将其视为一个新的、更小的 OT 问题。我们在这个子集上再次运行第二步。我们对所有子集都这样做。

第四步: 基准情况 我们重复这个过程，逐步提高分辨率 (或在数据集缩小时保持秩不变) 。最终，分区变得足够小 (例如，单点或非常小的组) ，我们可以精确地解决它们，或者它们已经微不足道地匹配了。

在最精细的尺度上，我们在原始海量数据集之间建立了一个双射——即一对一的映射。

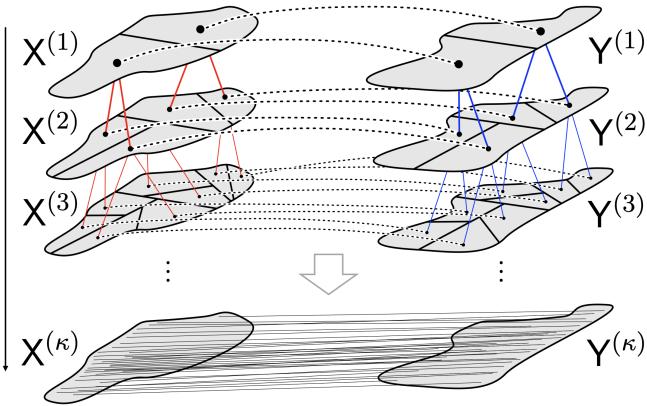
图 1: 显示递归分区的 Hierarchical Refinement 算法示意图。

如 图 1 所示，算法从顶部 (粗尺度) 流向底部 (细尺度) 。

  1. 顶部: 数据是一个大团块。
  2. 中间: 低秩 OT 将数据分割成匹配的子区域 (由连接特定子集的红线表示) 。
  3. 底部: 过程重复，直到每个点都被唯一配对。

形式化层级结构

算法在尺度 \(t\) 维护一组配对的分区，记为 \(\Gamma_t\)。

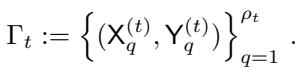
公式 11: 尺度 t 处分区集合 Gamma 的定义。

这里，\(\rho_t\) 是尺度 \(t\) 的总簇数。\(\Gamma_t\) 中的每个元素都是一对子集 \((X^{(t)}_q, Y^{(t)}_q)\)。

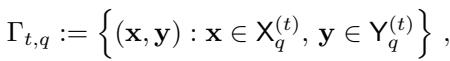
公式 10: 特定共聚类对的定义。

在循环的每一步，算法在当前活动的分区对上调用低秩 OT 求解器 (LROT):

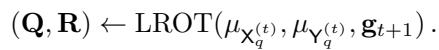
公式 13: 在子集上调用低秩 OT 求解器。

结果为下一个尺度 \(t+1\) 创建了更细的分区。

理论保证

这种分而治之的策略真的能降低传输成本，还是只是随意地分割数据？作者提供了一个命题 (命题 3.4) ，证明了传输成本随着每一步细化而降低 (或保持不变) 。

他们定义了每个尺度上的“隐式”块耦合 \(\mathbf{P}^{(t)}\)——这是一个我们从未在内存中实际构建的矩阵，但在概念上代表了当前的匹配状态。

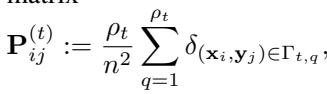
公式 14: 隐式块耦合定义。

该命题界定了细化层级之间的成本变化 \(\Delta_{t, t+1}\):

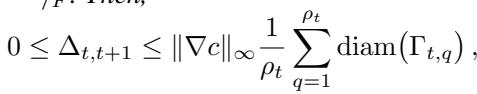
公式 15: 尺度间成本差异的上下界。

这个不等式至关重要。它指出成本的改善受限于成本函数的 Lipschitz 常数 \(\|\nabla c\|_\infty\) 和分区的 直径 。 随着算法的进行，分区变得越来越小 (\(\mathrm{diam}(\Gamma_{t,q})\) 减小) ，这意味着解收敛于最优的细粒度映射。

复杂度: 迈向“无限与超越”

HiRef 真正的美妙之处在于它的效率。

  • 空间复杂度: 线性 (\(O(n)\))。因为我们从未实体化完整的 \(n \times n\) 矩阵，我们只存储数据和当前的分区。
  • 时间复杂度: 对数线性 (\(O(n \log n)\)) 或接近于此，具体取决于特定的秩调度。

这种扩展行为使得 HiRef 能够处理那些会让标准 Sinkhorn 求解器立即崩溃的数据集。

为了最大化效率，作者甚至制定了一个优化问题，以选择最佳的秩序列 \((r_1, r_2, \dots, r_\kappa)\) 来分解数据集大小 \(n\):

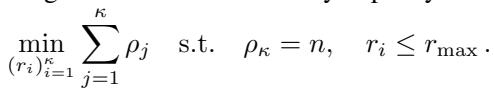
公式 17: 秩调度优化。

这确保了算法执行达到单点分辨率所需的最少工作量。

实验与结果

理论很完善，但在实践中效果如何？作者将 HiRef 与 Sinkhorn、ProgOT (另一种可扩展求解器) 以及标准的低秩方法进行了基准测试。

1. 合成数据基准测试: 准确性和质量

首先，他们在“半月形 (Half-Moons) ”和“S 曲线 (S-Curves) ”等合成数据集上测试了该方法，以可视化传输映射。

在下方的 图 2 中，我们可以看到原始 OT 代价 (移动质量所做的总“功”) 随样本大小的变化。

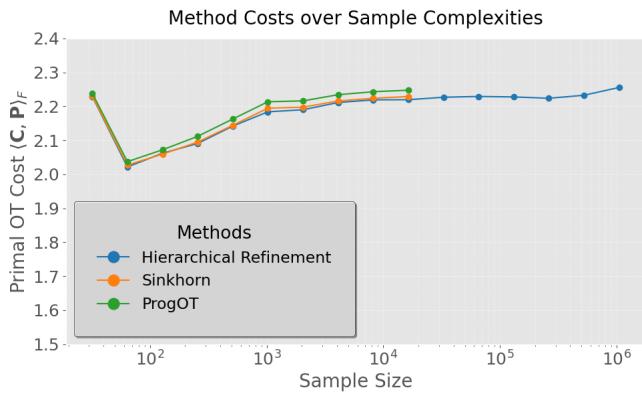
图 2: 原始 OT 代价对比与样本大小的关系。

  • 观察: HiRef (蓝线) 实现的传输代价几乎与 Sinkhorn (橙色) 和 ProgOT (绿色) 相同。它没有为了速度而牺牲质量。
  • 扩展性: 注意 X 轴。Sinkhorn 和 ProgOT 很早就停止了 (大约 \(10^4\) 个点) ，因为它们耗尽了内存。HiRef 轻松延续到了 \(10^6\) (一百万) 个点。

此外，HiRef 产生的是“硬”双射 (确定性映射) ，而 Sinkhorn 产生的是“软”概率耦合。这导致了更清晰的映射。

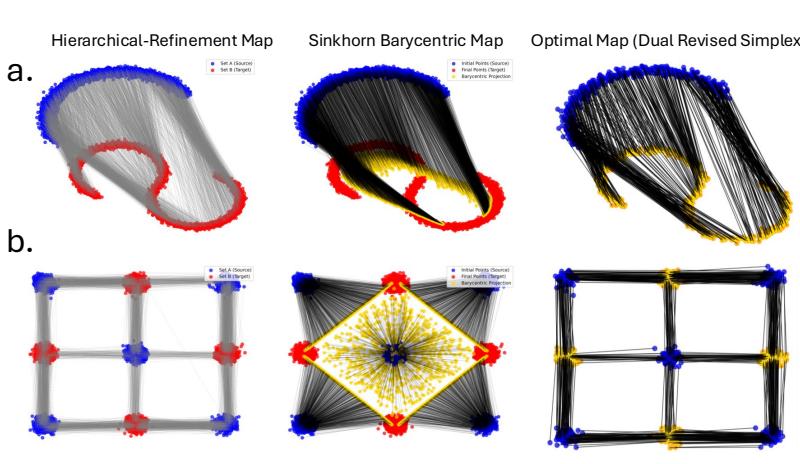
图 3: 传输映射的视觉对比。

在 图 3 中，对比 Hierarchical Refinement 映射 (顶行) 和 Sinkhorn 重心映射 (Barycentric Map) (中行) 。

  • Sinkhorn 映射经常将点拉向“平均值” (重心) ，导致目标形状收缩或看起来扭曲 (注意 a 行中 S 曲线的间隙) 。
  • HiRef 映射更忠实地保持了目标分布的几何形状，看起来非常接近真实的最佳映射 (底行) 。

2. 海量生物数据集: 小鼠胚胎发育

最优传输在生物学中被大量用于重建发育轨迹——弄清楚细胞如何随时间演变。作者将 HiRef 应用于小鼠器官发生 (MOSTA) 的大规模时空转录组学数据集。

他们对齐了发育时间点之间的细胞 (例如，第 13.5 天到第 14.5 天) 。这些数据集包含数十万个细胞。

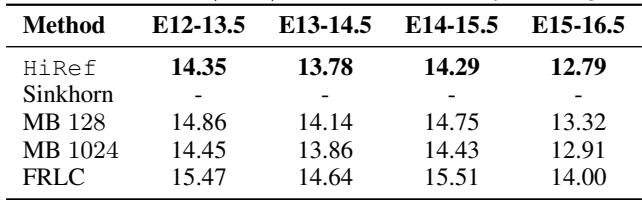
表 1: 小鼠胚胎各阶段的代价值。

表 1 显示了传输代价。

  • Sinkhorn: 对于所有大阶段均失败 (内存不足) 。
  • HiRef: 成功运行于所有配对。
  • 性能: 与小批量 (MB) 近似相比，HiRef 始终实现更低的传输代价 (越低越好) 。例如，在 E15-16.5 的过渡中，HiRef 的代价为 12.79 , 而大批量 OT 的代价为 12.91 。

3. 空间对齐: MERFISH 脑图谱

在另一个生物学实验中，他们仅基于空间坐标对齐小鼠大脑的切片，然后检查基因表达是否匹配。这是一个严格的测试: 如果空间对齐错误，生物学特征将无法匹配。

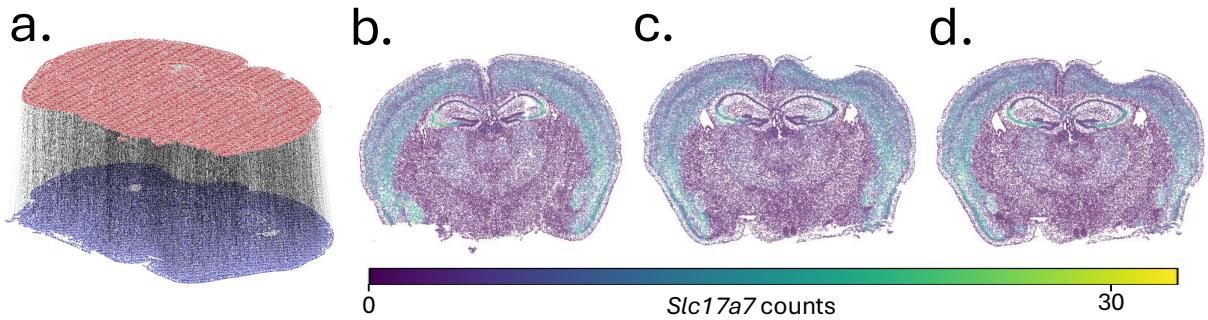
图 4: MERFISH 对齐结果。

图 4 可视化了结果。

  • a: 脑切片的 3D 对齐。
  • b, c, d: Slc17a7 的基因表达。
  • (b) 是源。
  • (d) 是真实目标。
  • (c) 是使用 HiRef 映射的 预测 目标。
  • 结果: 预测图 (c) 看起来与真实情况 (d) 几乎相同，余弦相似度为 0.8098 。 标准的低秩方法 (如 FRLC) 在这里表现挣扎，相似度得分要低得多 (约 0.23) 。这证明了 HiRef 的 细化 方面对于捕捉细粒度的局部结构是必要的。

4. 百万图像挑战: ImageNet

最后，是终极的扩展性展示。作者对齐了来自 ImageNet 数据集的 128 万张图像 (表示为 2048 维的嵌入) 。

表 2: ImageNet 对齐的代价值。

表 2 讲述了这个故事。

  • Sinkhorn / ProgOT / LOT: 无法运行 (内存/时间限制) 。
  • HiRef: 完成了任务，代价为 18.97 。
  • 小批量 (MB): 即使使用大批量大小 (1024)，代价也更高 (19.58)，表明对齐效果较差。

HiRef 成功在两个各包含超过一百万个点的数据集之间计算了全秩对齐——这在以前被认为是全局最优传输无法实现的壮举。

结论与启示

论文 “Hierarchical Refinement” 代表了计算最优传输的一次重大飞跃。通过结合低秩近似的速度和递归的多尺度策略，作者有效地拆除了阻碍 OT 发展的二次方障碍。

关键要点:

  1. 低秩因子即聚类: 该算法利用了低秩 OT 因子自然地将对应的源点和目标点分组的数学属性。
  2. 细化恢复分辨率: 通过递归解决更小的子问题，HiRef 恢复了标准低秩方法所平滑掉的细粒度 Monge 映射。
  3. 扩展性已解决: 凭借线性空间和对数线性时间，OT 现在可以应用于拥有数百万样本的数据集，而无需依赖有偏差的小批量处理。

这为什么重要? 这为在深度学习领域使用“真正的”最优传输打开了大门，而这些领域以前仅限于使用近似方法。我们可以看到更好的 生成模型 (更准确地将噪声对齐到数据) ，更精确的 生物轨迹推断 (追踪数百万个细胞) ，以及计算机视觉中改进的 领域自适应 。

HiRef 将“维度诅咒”转化为分而治之的机遇，证明了只要有正确的层级结构，我们确实可以将最优传输带向无限，超越极限。

本博客文章解读了 Halmos 等人 (2025) 的研究论文 “Hierarchical Refinement: Optimal Transport to Infinity and Beyond”。