透视思维: 利用流形几何解锁神经网络动力学

神经网络究竟是如何学习的？

如果你观察原始数据——数十亿个突触权重的变化——你看到的是一场浮点数调整的混沌风暴。如果你观察损失曲线，你看到的是一条向下的线。但这二者都无法告诉你网络如何构建信息。

很长一段时间以来，研究人员将深度学习划分为两个截然不同的机制: 懒惰机制 (Lazy regime) 和丰富机制 (Rich regime) 。 在懒惰机制中，网络几乎不触碰其内部特征，表现得像一个被美化的核机器 (kernel machine) 。在丰富机制中，网络积极地塑造复杂的、针对任务的特征。

但这种二分法过于简单。这就像把所有的交通方式要么归类为“步行”，要么归类为“短跑”，忽略了从自行车到飞机的所有中间状态。特征学习是一个谱系，充满了微妙的策略和独特的阶段。

在这篇文章中，我们将探索发表在 Feature Learning beyond the Lazy-Rich Dichotomy 中的一个新的分析框架。该框架利用表征几何 (Representational Geometry) 来窥探“黑盒”内部。通过将数据建模为在高维空间中移动的几何流形 (点云) ，我们可以可视化神经网络到底是如何解开复杂问题的——以及为什么它们有时无法泛化。

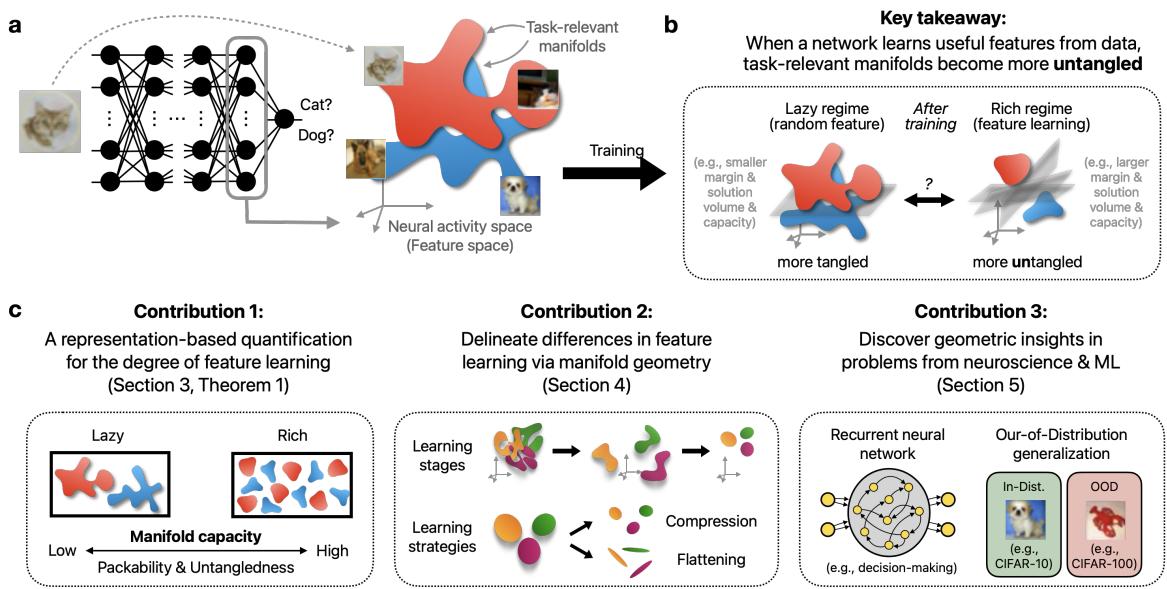
示意图展示了提出的框架。图 A 展示了任务相关流形的概念。图 B 展示了纠缠 (懒惰) 与解缠 (丰富) 流形之间的区别。图 C 概述了论文的贡献。

第一部分: “懒惰与丰富”的问题

为了理解这项工作的贡献，我们需要先理解当前的主流理论。

懒惰机制 (The Lazy Regime)

想象一个神经网络，其内部层是随机初始化的并且保持固定。只有最后一层 (分类器) 更新其权重以解决任务。这本质上就是“懒惰学习”的工作方式。网络不学习新特征；它只是弄清楚如何组合一开始就有的随机特征。在数学上，这种行为类似于核方法 (具体来说是神经正切核，或 NTK) 。

丰富机制 (The Rich Regime)

相比之下，现代深度学习通常在“丰富机制”下运作。在这里，内部权重发生显著变化。网络学会检测边缘，然后是纹理，再到物体部件。它建立了一个针对特定任务优化的特征层次结构。

差距

研究人员已经开发了一些指标来猜测网络处于哪种机制，例如跟踪权重偏离初始化的距离。然而，这些指标是代理测量 (proxy measurements) 。它们关注的是机制 (权重) 而不是结果 (表征) 。它们往往无法区分不同“风味”的丰富学习，也无法解释为什么网络可能学得很好但在新数据上无法泛化 (分布外，OOD) 。

我们需要一种方法来直接衡量所学特征的质量和结构 。

第二部分: 进入流形容量理论

作者提议将我们的关注点从单个神经元或权重转移到神经流形 (Neural Manifolds) 上。

什么是神经流形？

想象你在给网络展示狗的图片。每一张狗的图片都会在层的神经元之间产生独特的活动模式。如果你将这些模式绘制为高维空间中的点 (每个轴代表一个神经元) ，所有“狗”点的集合就形成了一团云。这团云就是类别流形 (Class Manifold) 。

如果网络表现良好，“狗”的流形应该与“猫”的流形截然不同。这个过程被称为流形解缠 (Manifold Untangling) 。

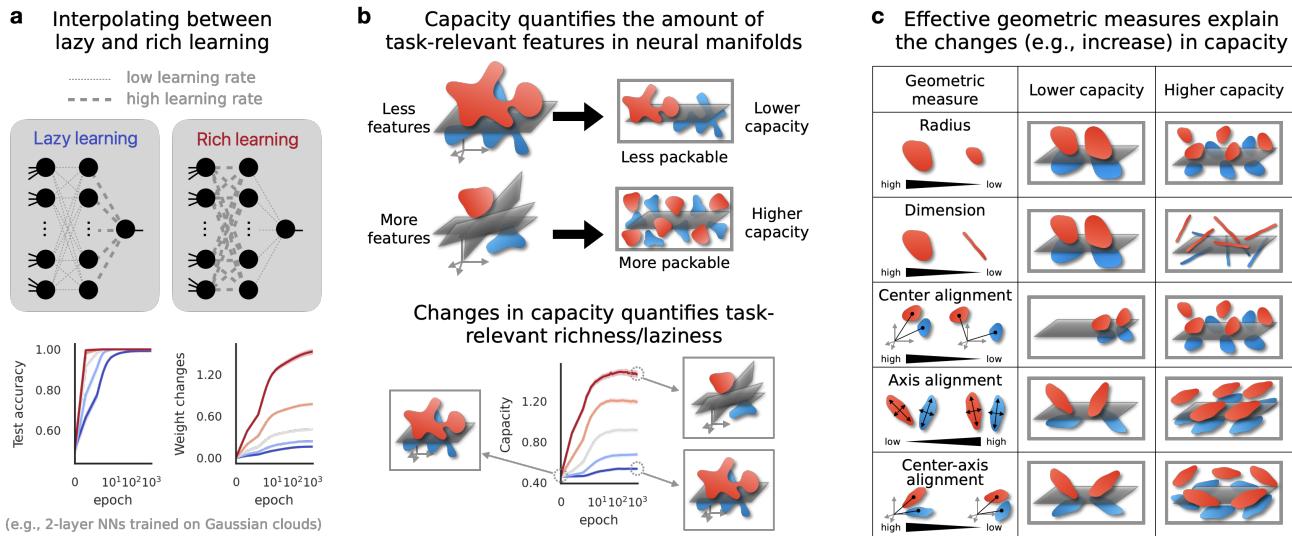
用容量衡量解缠

我们如何量化这些云团的分离程度？研究人员利用了一个叫做流形容量 (Manifold Capacity) 的概念。

把神经表征空间想象成一个物理容器。流形容量衡量的是，在这个空间中你可以塞入多少个不同的物体流形，同时仍然能够用线性平面 (线性分类器) 将它们分开。

  • 低容量: 流形纠缠在一起，体积庞大或混乱。你无法在空间中放入很多流形而不让它们重叠。
  • 高容量: 流形紧凑、致密且分离良好。你可以将许多不同的类别打包到同一个神经空间中。

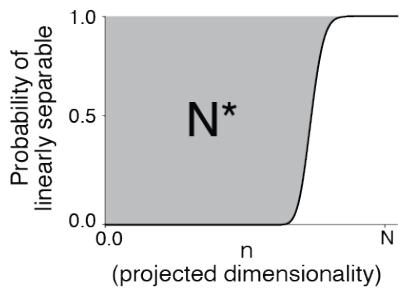
一张说明模拟容量的图表。随着投影维度 (n) 接近神经元数量 (N)，线性可分的概率增加。

如上图所示，容量与分离这些点所需的临界维度有关。虽然模拟定义很直观，但在大型网络中计算它的成本非常高。

平均场解决方案

为了使其具有实用性，作者使用了“平均场 (Mean-Field) ”理论定义 (\(\alpha_M\)) 。这使得他们能够利用流形的几何形状解析地计算容量。

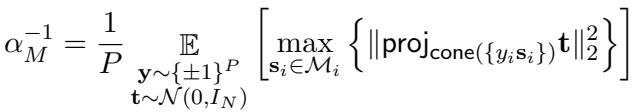
基于平均场理论的流形容量数学定义。

这里至关重要的见解是, 流形容量 (\(\alpha_M\)) 是特征学习“丰富度”的直接代理。 随着网络学习到更好的特征，它会解开流形，容量得分也随之上升。

第三部分: GLUE (与解缠效率相关的几何)

知道容量增加了很有用，但知道为什么增加则更加深刻。作者引入了一组称为 GLUE 的几何描述符。

一组流形的容量本质上由它们的大小、形状和方向决定。作者推导出了一个近似公式，将容量 (\(\alpha_M\)) 与两个主要的几何属性联系起来: 流形半径 (\(R_M\)) 和流形维度 (\(D_M\)) 。

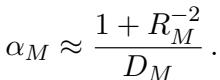
将流形容量与半径和维度联系起来的近似公式。

这个方程是表征几何中的“E=mc²”。它告诉我们神经网络可以通过两种方式改善其表征 (增加 \(\alpha_M\)) :

  1. 收缩半径 (\(R_M\)) : 使点云更小、更紧密。这降低了噪信比。
  2. 压缩维度 (\(D_M\)) : 将点云压扁，使它们在特征空间中占据更少的维度。

几何描述符

除了半径和维度，该框架还跟踪流形之间的相关性:

  • 中心对齐 (Center Alignment, \(\rho_M^c\)) : 不同类别云团的中心是否聚集在一起？
  • 轴对齐 (Axes Alignment, \(\rho_M^a\)) : 云团的“形状”是否朝向相同的方向？

通过跟踪这些指标，我们可以描述网络用于学习的策略。

几何测量示意图。图 A 展示了懒惰学习与丰富学习之间的插值。图 B 展示了容量如何量化丰富度。图 C 展示了 GLUE 指标: 半径、维度和对齐度。

第四部分: 验证指标

这种方法真的比仅仅观察权重变化更有效吗？

研究人员使用在合成数据上训练的 2 层神经网络设置了一个实验。他们利用一个“缩放因子” (\(\alpha\)) 来人为地迫使网络进入懒惰或丰富机制。较小的 \(\alpha\) 限制特征学习 (懒惰) ，而较大的 \(\alpha\) 鼓励特征学习 (丰富) 。

他们将流形容量与“权重变化”和“核对齐” (CKA) 等传统指标进行了比较。

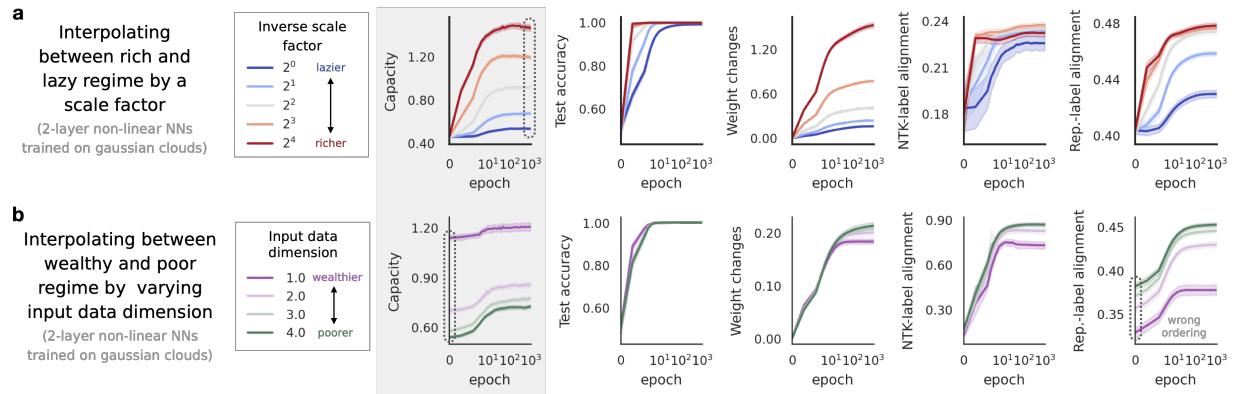
2 层网络中容量与其他指标的比较。图 A 展示了懒惰与丰富机制之间的插值。图 B 展示了初始化丰富度的插值。与其他指标相比，容量更一致地跟踪了真实情况 (缩放因子) 。

如上方的 图 4a 所示:

  • 测试准确率很快饱和；它无法区分“有点丰富”和“非常丰富”。
  • 权重变化在丰富机制下爆炸式增长，但缺乏细微差别。
  • 容量 (第一行) 显示出平滑、单调的增长，完美地跟踪了学习过程的真实丰富度。

这不仅仅是一个经验性的观察；作者为 2 层网络提供了理论证明 (定理 3.1) ，表明容量在数学上跟踪了一个梯度步后的有效丰富度。

第五部分: 揭示隐藏的学习动力学

这就是该框架大放异彩的地方。由于流形容量由几何子分量 (半径、维度、对齐) 组成，我们可以分解学习过程，看看网络是如何解决问题的。

学习策略: 压缩 vs. 扁平化

作者发现网络并不总是以相同的方式学习。通过在半径与维度的平面上绘制学习轨迹，他们确定了独特的策略。

  • 策略 1: 先压缩半径，然后降低维度。
  • 策略 2: 牺牲半径 (让流形稍微膨胀) ，以激进地降低维度。

学习阶段

也许最迷人的发现是，即使准确率曲线看起来像一条平滑的线，特征学习也是在不同的阶段发生的。

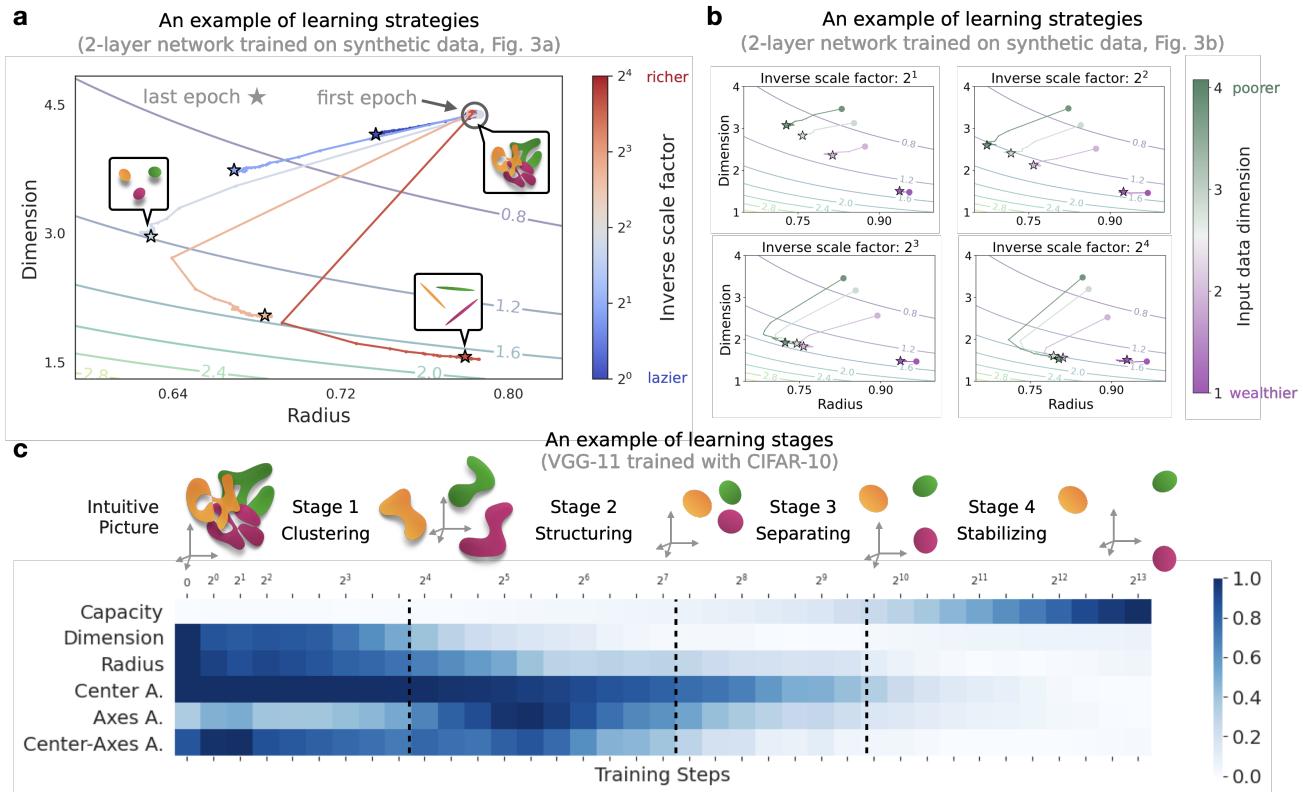
学习策略和阶段的可视化。图 A 和 B 展示了半径与维度的等高线图。图 C 展示了在 CIFAR-10 上训练的 VGG-11 的归一化动力学，揭示了明显的几何演化阶段。

观察图 5c (上图) , 我们可以在 CIFAR-10 上训练的深度网络 (VGG-11) 中识别出四个明显的阶段:

  1. 聚类阶段 (Clustering Stage) : 网络迅速将类别流形聚拢在一起。
  2. 结构化阶段 (Structuring Stage) : 随着网络弄清楚类别之间的关系，几何相关性 (对齐度) 增加。
  3. 分离阶段 (Separating Stage) : 对齐度下降，因为网络将不同的类别推开以最大化边界。
  4. 稳定阶段 (Stabilizing Stage) : 几何结构稳定在最终配置。

标准的准确率指标完全忽略了表面之下发生的这出好戏。

第六部分: 在神经科学和机器学习中的应用

这个框架的力量不仅限于分析玩具模型。作者将其应用于两个主要的开放问题。

1. 循环神经网络中的结构性偏置 (神经科学)

在神经科学中，很难直接测量突触权重。我们通常只能记录神经活动。这使得“基于权重”的分析变得不可能。

作者分析了在认知任务上训练的循环神经网络 (RNN) 。之前的工作表明，连接的初始化 (具体来说是权重矩阵的秩) 会使网络偏向于懒惰或丰富学习。

利用流形容量，他们发现了一个微妙的结果:

  • 具有不同初始化的 RNN 实际上达到了相同的最终容量。
  • 然而，它们通过完全不同的几何路径到达那里。低秩初始化依赖于改变维度，而高秩初始化依赖于改变半径。

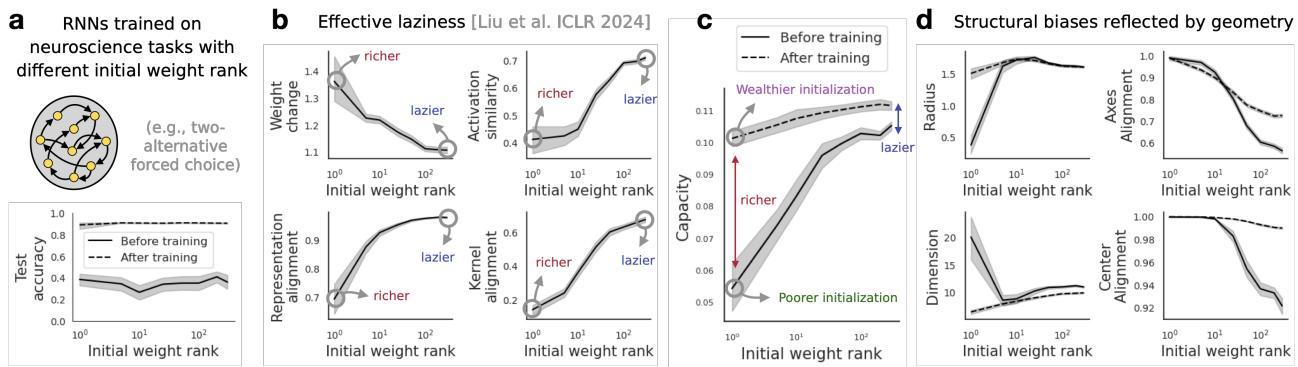
RNN 的分析。图 C 显示不同的初始化达到相似的最终容量，但起点不同。图 D 显示它们表现出完全不同的几何配置 (半径 vs 维度) 来实现该容量。

这表明大脑回路的“结构性归纳偏置”决定了它如何学习，即使最终的表现是相似的。

2. 分布外 (OOD) 泛化 (机器学习)

深度学习的一个主要顽疾是 OOD 失败: 模型在训练数据 (例如 CIFAR-10) 上表现出色，但在稍有不同的数据 (例如 CIFAR-100 或受损图像) 上却失败了。

传统观点可能认为“越丰富越好”。如果网络学到了更多的特征，它难道不应该泛化得更好吗？

作者发现了一个反直觉的结果: “超丰富 (Ultra-Rich) ”机制会损害 OOD 泛化。

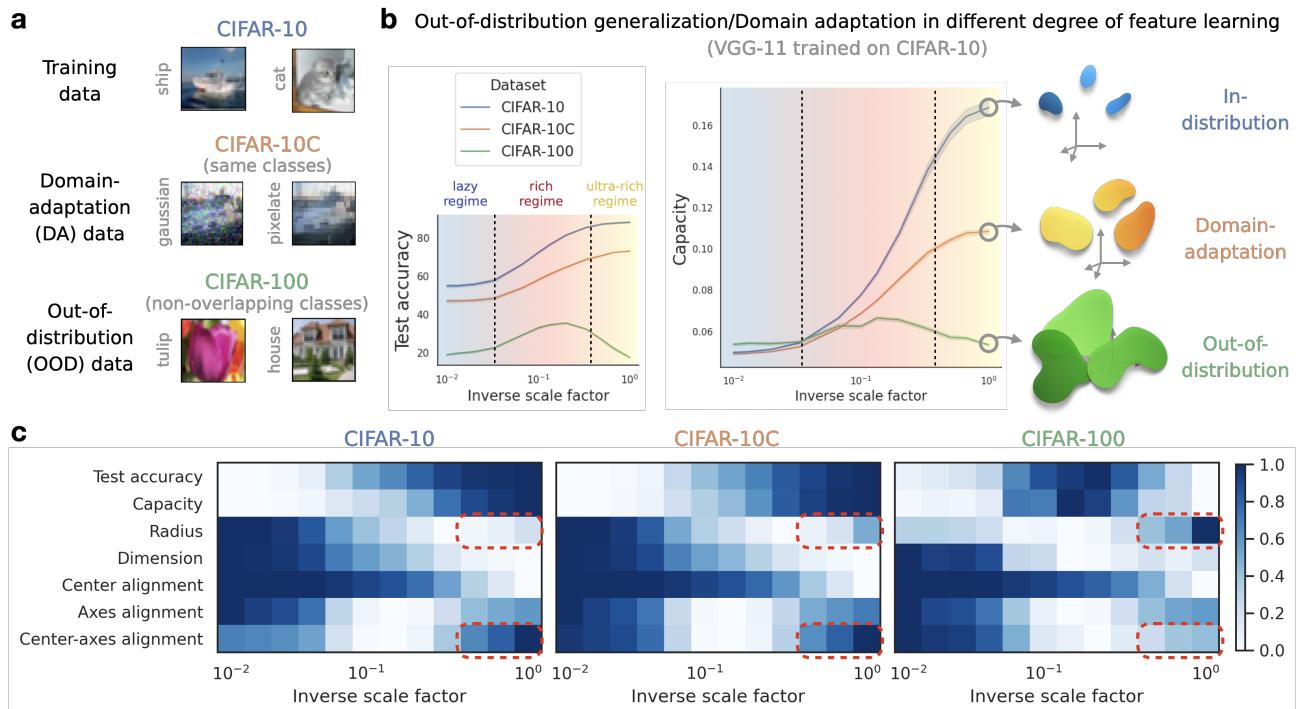
OOD 泛化分析。图 B 显示在超丰富机制下，OOD 数据 (CIFAR-100) 的测试准确率下降。图 C 揭示了这是由流形半径的膨胀和中心-轴对齐的增加驱动的。

如图 7 所示，当网络被推入“超丰富”机制 (x 轴的最右侧) 时:

  1. 分布内准确率 (CIFAR-10) 保持很高。
  2. OOD 准确率 (CIFAR-100) 崩塌 。

为什么？几何分析给出了答案: 在超丰富机制中, 流形半径膨胀 , 并且中心-轴对齐增加 。 网络过度优化了训练数据，创建了“疏松”、高度对齐的流形，这些流形对于特定的训练类别是线性可分的，但在面对新类别时，结构上却很脆弱。

结论

“懒惰与丰富”的二分法作为一阶近似，已经很好地服务了社区，但这已不再足够。正如本文所展示的，特征学习是一个复杂的几何过程，涉及高维流形的压缩、结构化和解缠。

通过使用流形容量和 GLUE 指标，我们获得了一套诊断工具集，它是:

  1. 基于表征的: 它作用于激活值，而不不仅仅是权重。
  2. 数据驱动的: 它不需要关于数据分布的假设。
  3. 机械性的: 它解释了性能提升或下降的原因。

这种几何视角开启了新的大门。对于神经科学家来说，它允许仅使用活动记录来分析大脑的可塑性。对于机器学习从业者来说，它提供了一种在部署前检测过拟合和预测 OOD 失败的新方法——只需观察数据云的形状。

特征学习不仅仅是移动权重；它是关于几何的。而现在，我们要这把尺子来衡量它。