你是否想过，为什么几乎每一个卷积神经网络 (CNN) 的第一层看起来都一样？无论你是在训练网络对狗进行分类、识别汽车，还是检测肿瘤，第一层的滤波器几乎总是收敛到特定的模式: 定向的边缘和被称为 Gabor 滤波器的振荡纹理。

这种现象是深度学习中最稳健的经验事实之一。它反映了哺乳动物视觉皮层的生物学特性，后者也使用类似的边缘检测器来处理视觉信息。但是，为什么会发生这种情况？更重要的是，从原始像素中学习这些特征背后的数学机制是什么？

近期一篇题为 “Feature learning from non-Gaussian inputs: the case of Independent Component Analysis in high dimensions” (从非高斯输入中学习特征: 高维独立成分分析案例) 的研究论文通过将深度学习与一种经典算法——独立成分分析 (ICA) ——联系起来，探讨了这个问题。

在这篇文章中，我们将深入剖析这篇论文。我们将探讨为何 ICA 是理解特征学习的绝佳试验场，为何标准算法在高维空间中举步维艰，以及“平滑”损失景观如何能够大幅减少学习所需的数据量。

第一层之谜

让我们从视觉证据开始。当我们在像 ImageNet 这样的大规模自然图像数据集上训练像 AlexNet 这样的深度网络时，权重会通过调整来提取有用的特征。

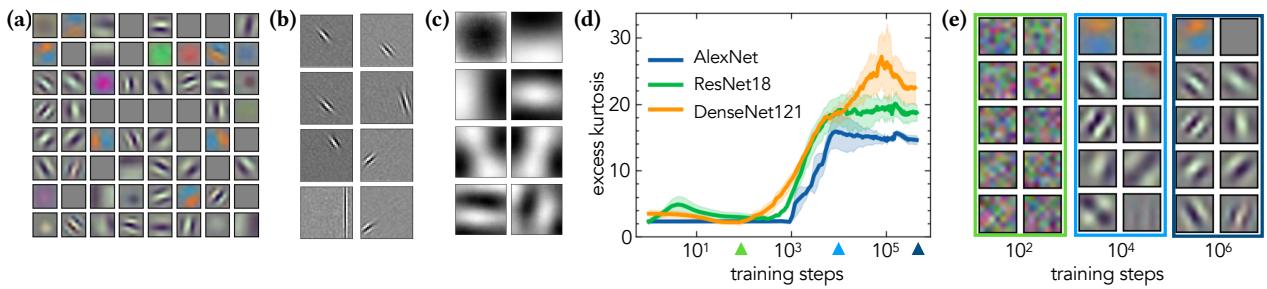
CNN、ICA 和 PCA 滤波器的比较。图 (a) 显示 AlexNet 滤波器，(b) 显示 ICA 滤波器，(c) 显示 PCA 滤波器。图 (d) 绘制了训练期间的超额峰度。

如上图 Figure 1 所示:

  • 图 (a) 展示了 AlexNet 第一层学习到的滤波器。它们是局部化的、有方向的，且类似于 Gabor 滤波器。
  • 图 (b) 展示了 ICA 在图像块上学习到的滤波器。注意到了惊人的相似性吗？ICA 也学习到了类 Gabor 滤波器。
  • 图 (c) 展示了主成分分析 (PCA) 学习到的滤波器。这些看起来完全不同——它们是全局的、类似棋盘的模式，并不能很好地捕捉边缘。

深度学习 (DL) 和 ICA 之间的这种相似性表明，它们由同一个底层原理驱动: 非高斯性 (Non-Gaussianity) 。

自然图像是高度非高斯的。天空、草地和皮肤的纹理并不遵循简单的钟形曲线分布。ICA 专门用于寻找这些非高斯方向。研究人员认为，ICA 可以作为一个“简化但原则性”的模型，用来研究深度网络如何学习特征。

什么是独立成分分析 (ICA) ？

要理解论文的发现，我们首先需要定义 ICA 实际上是做什么的。

想象你在一个鸡尾酒会上。你有两个麦克风正在录制房间的声音。你听到的是两个人同时说话的混合声音。ICA 是一种可以将这些混合信号分离回两个独立声音的算法。

在数学上，ICA 假设数据是独立非高斯源的线性混合。目标是找到一个由权重向量 \(w\) 定义的投影方向，使得投影后的数据尽可能“非高斯”。

ICA 的目标函数如下所示:

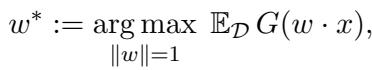
最大化期望非高斯性的 ICA 目标函数方程。

这里，\(w^*\) 是我们要寻找的最佳方向，而 \(G\) 是一个衡量非高斯性的 对比函数 (contrast function) 。 如果数据是高斯的，这个函数就无法帮助我们找到有趣的方向 (因为高斯分布从各个角度看都是一样的) 。但由于我们的“信号”是非高斯的，最大化 \(G(w \cdot x)\) 会指引我们找到特征。

对比函数 \(G(s)\) 的常见选择包括:

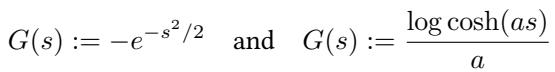
ICA 中使用的标准对比函数。

第一种选择 (负指数) 对异常值具有鲁棒性，而第二种选择与峰度 (分布的“长尾性”) 有关。

高维问题

这里是论文从观察转向严谨分析的地方。在现代机器学习中，我们处理的是 高维数据 (\(d\) 很大) 。一个 \(64 \times 64\) 的图像块就有 4,096 个维度。

关于 ICA 的经典理论关注的是渐近收敛 (当我们有无限时间时会发生什么) 。但在高维空间中，主要的瓶颈不是 收敛速度，而是 搜索阶段 (search phase) 。 算法从随机权重开始。在一个巨大的 4000 维空间中，算法需要多少样本 (\(n\)) 才能 找到 正确的方向并摆脱随机性？

作者研究了两种主要算法:

  1. FastICA: 业界标准的 ICA 算法。
  2. 随机梯度下降 (SGD) : 用于训练神经网络的算法。

合成设置: 尖峰累积量模型

为了精确测量性能，作者使用了一个受控的合成数据模型，称为 尖峰累积量模型 (Spiked Cumulant Model) 。

想象一个数据集，其中数据在除了 一个 方向之外的所有方向上都看起来像标准高斯噪声。在那一个特殊方向 (“尖峰”或信号 \(v\)) 上，数据遵循非高斯分布。

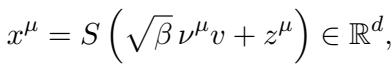
带噪 ICA 数据模型方程。

这里:

  • \(x^\mu\) 是输入向量。
  • \(v\) 是隐藏的非高斯方向 (我们想要学习的特征) 。
  • \(\nu^\mu\) 是潜在的非高斯信号 (例如，随机 \(\pm 1\) 值) 。
  • \(z^\mu\) 是高斯噪声。
  • \(S\) 是白化矩阵 (确保我们不能通过简单的方差/PCA 方法作弊) 。

白化矩阵定义为:

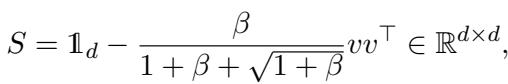
白化矩阵 S 的定义。

这种设置创造了一个“大海捞针”的问题。算法必须处理 \(n\) 个样本，才能在 \(d\) 维空间中找到隐藏的向量 \(v\)。

结果 1: FastICA 需要海量数据

FastICA 是一个不动点算法。它使用整个数据集 (大批量) 一次性更新其权重估计 \(w\)。更新规则如下:

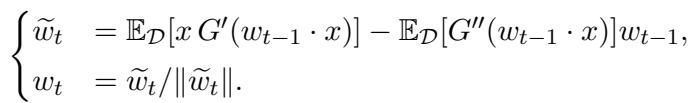
FastICA 更新规则。

它由两部分组成: 一个类梯度项和一个正则化项。这种正则化以使 FastICA 在 接近 解时收敛非常快 (二次方级) 而闻名。

但它能从随机开始找到解吗?

作者证明了一个惊人的结果。为了在高维空间中恢复单个非高斯方向，FastICA 的样本数 \(n\) 必须随维度 \(d\) 的 四次方 缩放。

\[n \gtrsim d^4\]

在高维统计的世界里，\(d^4\) 是一场灾难。如果你的输入维度只有 100，你需要 \(100^4 = 100,000,000\) 个样本。

研究人员通过实验证实了这一理论界限。请仔细看 Figure 2 :

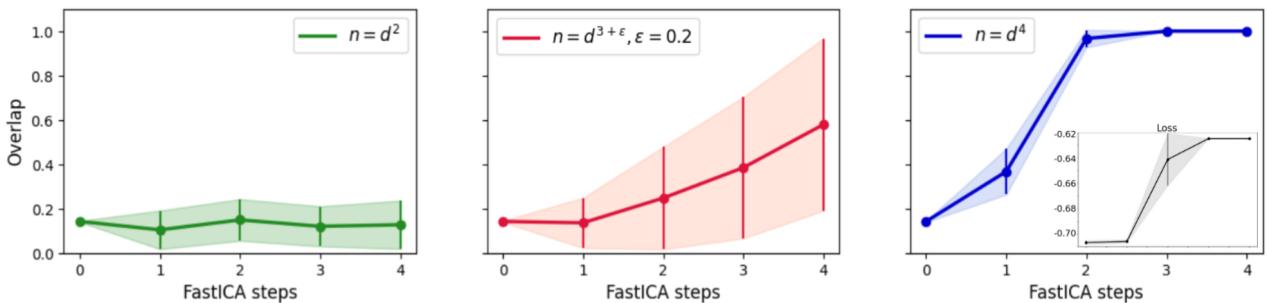
FastICA 在不同样本复杂度范围内的合成数据上的表现。

  • 左图 (\(n = d^2\)): 算法失败。重叠度 (Overlap，即学习到的权重与真实特征的相似度) 保持在低位，接近随机基线。
  • 中图 (\(n = d^{3.2}\)): 它在挣扎，缓慢攀升但不稳定。
  • 右图 (\(n = d^4\)): 成功！重叠度非常快地跳升至接近 1.0 (完美恢复) 。

这证实了理论: FastICA 在高维空间的搜索阶段数据效率极低。

为什么这么难？信息指数

为什么需要 \(d^4\) 个样本？数学解释涉及 信息指数 (Information Exponent, \(k^*\)) 。

总体损失函数可以根据我们的权重与真实信号之间的重叠度 \(\alpha\) 展开成一系列项。

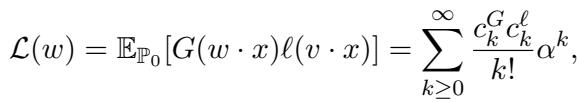
损失函数的 Hermite 展开。

因为数据已经过白化 (协方差为单位矩阵) ，这个展开式的前几项消失了。对于这个特定的 ICA 问题，第一个非零项出现在 四阶 (\(k^* = 4\)) 。

粗略地说，“信号”强度按 \(\alpha^{k^*-1}\) 缩放。在初始化时，我们在随机猜测，所以我们的重叠度 \(\alpha\) 很小 (\(\approx 1/\sqrt{d}\)) 。这使得信号极弱——按 \(d^{-3/2}\) 缩放。与此同时，噪声随样本大小缩放。为了从噪声中分辨出那个微小的信号，你需要与 \(d^{k^*}\) 成比例的大量样本。

结果 2: SGD 与平滑景观

如果 FastICA 需要 \(d^4\) 个样本，有没有更好的方法？

作者转向了 随机梯度下降 (SGD) , 这是深度学习的主力。他们分析了 在线 SGD (Online SGD) , 即一次更新一个样本的权重。

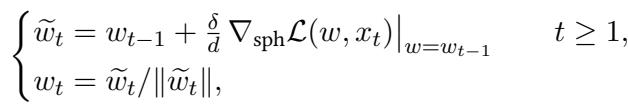
在线球面 SGD 更新规则。

先前工作的理论表明，标准的在线 SGD 需要 \(n \approx d^{k^*-1}\) 个样本。由于 \(k^*=4\)，普通 SGD 应该需要 \(n \approx d^3\) 个样本。这比 FastICA (\(d^4\)) 好，但仍然相当昂贵。

然而，作者引入了一个强大的修改: 平滑 SGD (Smoothed SGD) 。

平滑损失

高维优化的问题在于，损失景观在初始化点 (鞍点) 周围通常非常平坦。梯度微小且充满噪声，使得很难看清哪个方向是“下坡”。

平滑涉及将损失函数与高斯核进行卷积。我们不再查看确切点 \(w\) 的损失，而是查看 \(w\) 周围小邻域内的平均损失。

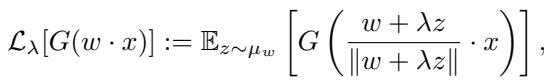
平滑损失函数的定义。

这里，\(\lambda\) 控制平滑的半径。较大的 \(\lambda\) 意味着我们看得更远。

为什么这有帮助? 想象你在一个广阔平坦的平原上徒步，寻找一个隐藏的很窄、很陡峭的峡谷 (最小值) 。如果你站在平原上，你看不到任何坡度。但如果你“平滑”地形，深峡谷的影响就会扩散开来，在平原上形成一个指向峡谷的缓坡。

直观地说，平滑改变了零点附近 (我们要开始的地方) 的损失函数形状:

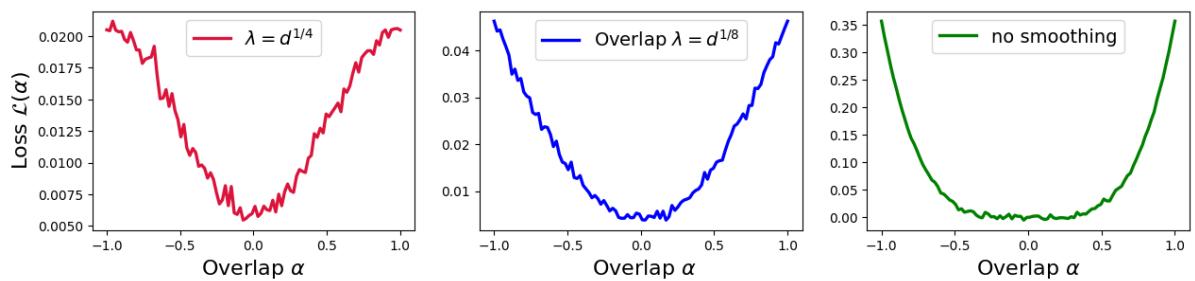
可视化平滑损失景观的好处。

  • 绿线 (无平滑) 在底部是平坦的。很难找到梯度。
  • 红线 (大平滑 \(\lambda = d^{1/4}\)) 更尖锐且呈 V 形。即使我们离解很远，它也能提供更强的梯度信号。

缩小差距

作者证明，通过精心选择平滑参数 \(\lambda\)，他们可以将 SGD 的样本复杂度从 \(d^3\) 降低到 \(d^2\) 。

这个 \(n \approx d^2\) 的阈值意义重大，因为它代表了这种设定下多项式时间算法的 计算极限 。

Figure 3 中的实验证实了这种层级关系:

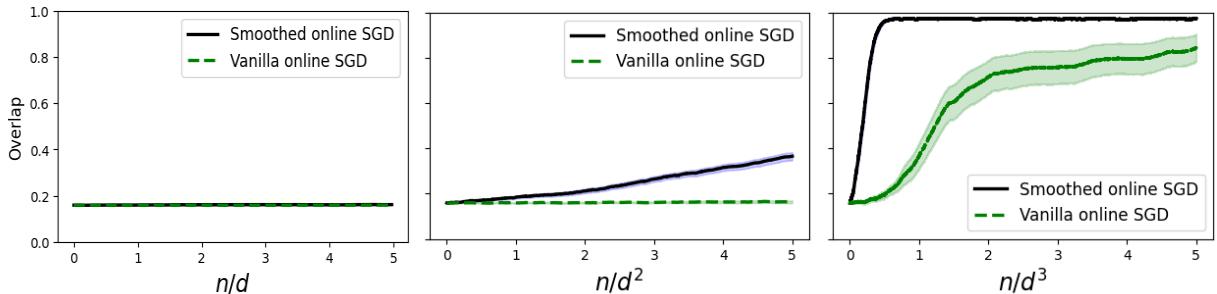
平滑 SGD 与普通 SGD 的性能比较。

  • 左 (\(n \propto d\)): 两种算法都不起作用。
  • 中 (\(n \propto d^2\)): 平滑 SGD (黑线) 恢复了信号！普通 SGD (绿色虚线) 失败。
  • 右 (\(n \propto d^3\)): 现在两种算法都起作用了。

这表明平滑有效地“增强”了信号，使网络能够用更少的数据学习特征。

回到现实: ImageNet 上的 FastICA

我们已经确定，在合成数据上，FastICA 效率低下 (\(d^4\)) ，而平滑 SGD 是最优的 (\(d^2\)) 。但是等等——我们在引言中不是看到 FastICA 在真实图像上效果很好吗？

作者回到 ImageNet 数据集来测试 FastICA 的实际表现。

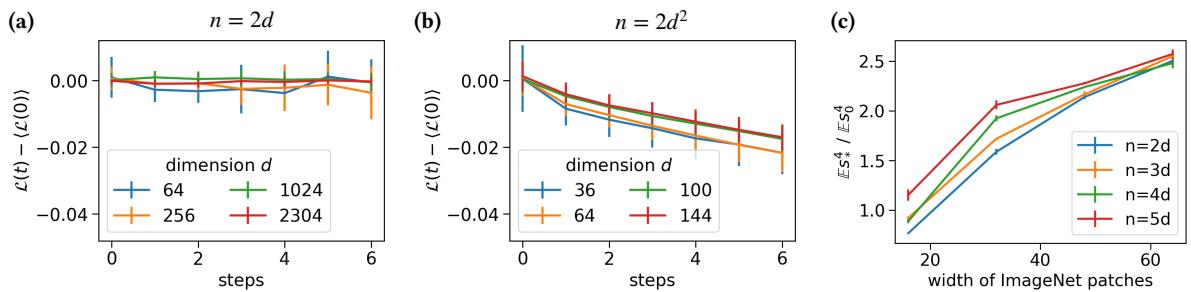
FastICA 在 ImageNet 图像块上的表现。

在 Figure 4 中:

  • 图 (a): 在线性样本数 (\(n=2d\)) 下，FastICA 卡住了。
  • 图 (b): 在二次方样本数 (\(n=2d^2\)) 下，FastICA 成功 降低了损失。

等一下，我们不是刚证明 FastICA 需要 \(d^4\) 个样本吗？为什么它在真实图像上 \(d^2\) 就行了？

答案在于真实数据的 信噪比 (SNR) 。 合成的“尖峰累积量模型”假设隐藏信号有些微妙 (特定的统计属性) 。然而，自然图像是 极端 非高斯的。它们具有重尾和强峰度。

作者测量了 ImageNet 中非高斯信号的“强度” (图 c) ，发现它比合成模型高得多。真实图像中这种巨大的固有信号补偿了 FastICA 的低效率。真实数据中的“尖峰”是如此巨大，以至于即使是次优算法也能很快找到它。

结论: 对深度学习的启示

这篇论文带我们经历了一段旅程，从 CNN 滤波器的视觉相似性到特征学习的硬性数学限制。

以下是关键要点:

  1. ICA 是特征学习的有效模型: 它仅通过最大化非高斯性就解释了 Gabor 滤波器的出现。
  2. FastICA 存在“搜索阶段”问题: 在高维空间中，标准算法可能会陷入盲目搜索信号的困境，理论上需要 \(n \approx d^4\) 个样本。
  3. 平滑很强大: 通过平滑损失景观，我们可以加速 SGD 以最佳样本效率 (\(n \approx d^2\)) 进行学习。这模仿了神经网络 (通常固有地平滑其输入或梯度) 可能的操作方式。
  4. 真实数据很宽容: 自然图像的强非高斯结构使得特征学习比最坏情况下的理论界限更容易。

理解这些动态有助于解释为什么深度学习在图像上效果如此之好，并表明像损失平滑这样的技术对于数据不像 ImageNet 那样“明显”的领域可能至关重要。